IMPLEMENTING

SPATIAL DATA WAREHOUSE HIERARCHIES IN

OBJECT-RELATIONAL DBMSs

Elzbieta Malinowski

∗

and Esteban Zim

anyi

Computer & Decision Engineering Department, Universit

e Libre de Bruxelles

50 av.F.D.Roosevelt, 1050 Brussels, Belgium

Keywords:

Spatial data warehouses, spatial hierarchies, implementation of spatial hierarchies.

Abstract:

Spatial Data Warehouses (SDWs) allow to analyze historical data represented in a space supporting the

decision-making process. SDW applications require a multidimensional view of data that includes dimensions

with hierarchies and facts with associated measures. In particular, hierarchies are important since traversing

them users can analyze detailed and aggregated measures. To better represent users’ requirements for SDWs,

the conceptual model with spatial support should be used. Afterwards, the conceptual schema is translated to

the logical and physical schemas. However, during the translation process the semantics can be lost. In this

paper, we present the translation of spatial hierarchies from the conceptual to physical schemas represented

in the MultiDimER model and Oracle 10g Spatial, respectively. Further, to ensure the semantic equivalence

between the conceptual and the physical schemas, integrity constraints are exempliﬁed mainly using triggers.

1 INTRODUCTION

Data warehouses (DWs) store and provide access to

large volumes of historical data. They usually are rep-

resented as a star schema, consisting of fact and di-

mension tables. A fact table contains numeric data

called measures. Dimensions are used for explor-

ing the measures from different analysis perspectives.

They usually contain hierarchies that allow to analyze

detailed or aggregated measures using the drill-down

and roll-up operations of OLAP systems.

It is estimated that about 80% of data stored in

databases has a spatial or location component, there-

fore, the location dimension has been widely inte-

grated in DW and OLAP systems. This dimen-

sion is usually represented in an alphanumeric, non-

cartographic manner (i.e., using the place name).

Nevertheless, it is well known that the inclusion of

spatial data in the analysis process can help to reveal

patterns that are difﬁcult to discover otherwise.

On the other hand, spatial databases (SDBs) al-

low to store and manipulate spatial objects. The latter

∗

The

work of E. Malinowski was funded by a scholar-

ship of the Cooperation Department of the Universit

e Libre

de Bruxelles. She is currently on leave from the Universi-

dad de Costa Rica.

correspond to real-world entities, for which the ap-

plication needs to keep their spatial characteristics.

Spatial objects consist of a thematic (or descriptive)

component and a spatial component. The former is

represented using traditional DBMS data types, e.g.,

integer, string. The spatial component includes its ge-

ometry, which can be of type point, line, surface, or

a collection of these types. Spatial objects can relate

to each other forming topological relationships (e.g.,

intersects, inside), i.e., the relationships that do not

change when spatial objects are rotated, scaled, etc.

Spatial Data Warehouses (SDWs) combine DWs

and SDBs for managing signiﬁcant amounts of his-

torical data that include spatial location. To better

represent users’ requirements for SDW applications,

a conceptual multidimensional model, such as Mul-

tiDimER (Malinowski and Zim

anyi, 2004) should be

used. Then, the conceptual speciﬁcations are trans-

lated into the logical and physical models. How-

ever, during this translation semantics may be lost due

to the limited expressive power of current DBMSs.

Therefore, an additional programming effort is re-

quired to ensure the correctness of this translation.

In this paper, we refer to the object-relational (0R)

implementation of SDW hierarchies. As an exam-

ple of a DBMS we use Oracle 10g Spatial. We also

186

Malinowski E. and Zimányi E. (2007).

IMPLEMENTING SPATIAL DATA WAREHOUSE HIERARCHIES IN OBJECT-RELATIONAL DBMSs.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - DISI, pages 186-191

DOI: 10.5220/0002355401860191

 SciTePress

implement integrity constraints to ensure semantic

equivalence between the conceptual and the physical

schemas. Section 2 presents works related to multidi-

mensional conceptual models with spatial elements.

Section 3 brieﬂy describes the MultiDimER model; it

also refers to topological relationships and their im-

portance in establishing the complexity of aggrega-

tion procedures. Section 4 includes the implementa-

tion of spatial hierarchies in OR databases. Finally,

Section 5 gives the conclusions.

2 RELATED WORK

To our knowledge, very few conceptual models based

on a multidimensional view of spatial data have been

proposed. For example, (Bimonte et al., 2005) deﬁne

a spatial multidimensional model with measures and

dimensions represented as complex objects.

(Pedersen and Tryfona, 2001) extend the work of

(Pedersen et al., 2001) by inclusion of spatial mea-

sures. They focus on the problems of aggregations

in the presence of different topological relationships

existing between spatial measures.

On the other hand, (Jensen et al., 2004) extend the

model proposed by (Pedersen and Tryfona, 2001) al-

lowing to include spatial objects in hierarchies with

partial containment relationships, i.e., where only part

of spatial object belongs to a higher hierarchy level

Several authors deﬁne elements of SDWs, i.e.,

spatial measures and dimensions, e.g., (Fidalgo et al.,

2004; Rivest et al., 2001; Stefanovic et al., 2000).

Other works use SDW concepts for developing spatial

OLAP (SOLAP) systems ((Han et al., 1997; Rivest

et al., 2001; Shekhar and Chawla, 2003)).

Nevertheless, the above-mentioned authors do not

refer to implementation issues of schemas created us-

ing the conceptual models or to aspects of logical rep-

resentation of data required for SOLAP applications.

3 THE MULTIDIMER MODEL

3.1 Model Deﬁnition

The MultiDimER model (Malinowski and Zim

anyi,

2004; Malinowski and Zim

anyi, 2005) allows to rep-

resent at the conceptual level the elements required

for SDW and SOLAP applications. The description

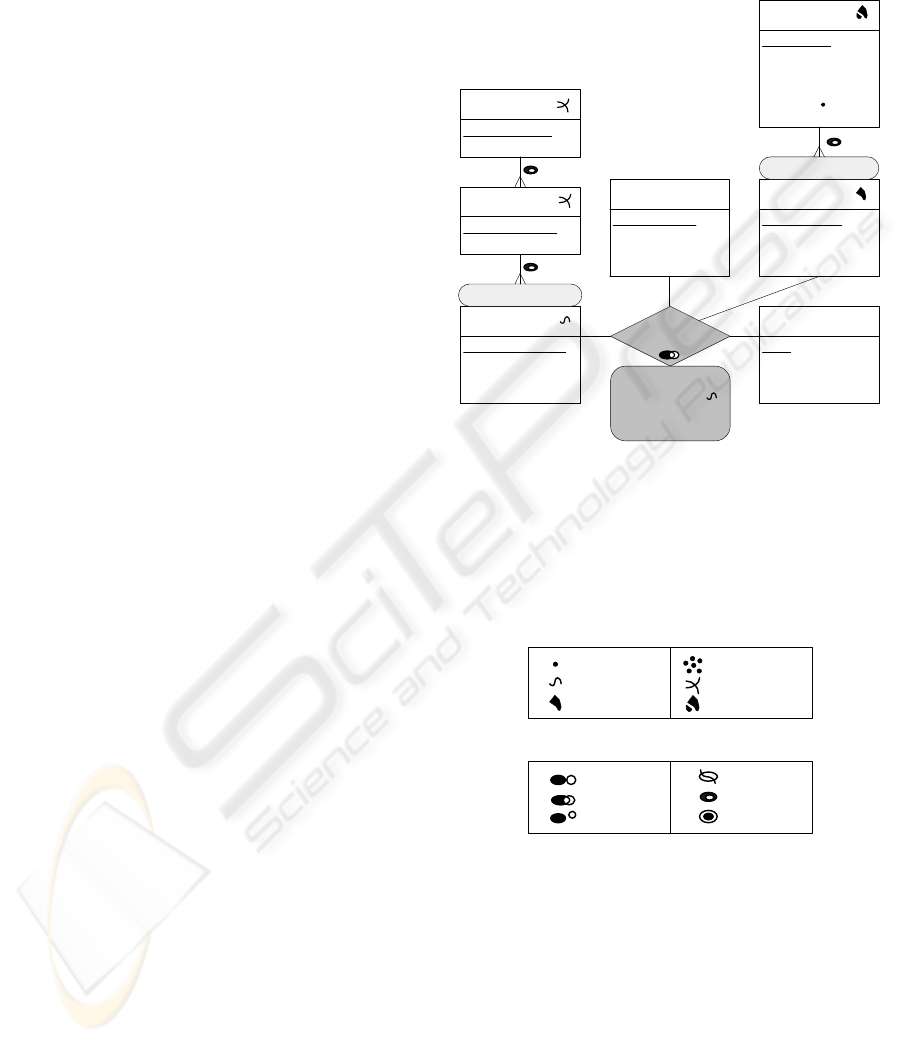
of the model is based on the schema in Figure 1 used

for the analysis of highway maintenance costs. The

schema contains dimensions, hierarchies, a fact rela-

tionship, and measures. A dimension is an abstract

concept for grouping data that shares a common se-

mantic meaning within the domain being modeled. It

represents either a level or one or more hierarchies.

Highway

segment

Segment number

Road condition

Speed limit

...

Time

Date

Event

Season

...

Highway structure

Highway

section

Section number

...

Highway

Highway name

...

Road coating

Coating name

Coating type

Coating durability

...

County

County name

County population

County area

...

Geo location

Highway

maintenance

Length (S)

Common area

No. cars

Repair cost

State

State name

State population

State area

State major activity

Capital

...

Figure 1: An example of multidimensional schema with

spatial elements.

A level corresponds to an entity type in the ER

model and represents a set of instances called mem-

bers that have common characteristics. For example,

Road coating in Figure 1 is a one-level dimension.

Point

Line

Surface

Point bag

Line bag

Surface bag

Adjacent

Intersect

Disjoint

Cross

Within

Equal

Figure 2: Pictograms for a) spatial data types and b) topo-

logical relationships.

Spatial levels are levels for which the application

needs to keep their spatial characteristics. This is cap-

tured by its geometry, which in the model is repre-

sented using the pictograms shown in Figure 2 a). In

Figure 1, we have ﬁve spatial levels: County, State,

Highway segment, Highway section, and Highway.

Hierarchies are required for establishing mean-

ingful paths for the roll-up and drill-down operations.

They contain several related levels, e.g., the County

IMPLEMENTING SPATIAL DATAWAREHOUSE HIERARCHIES IN OBJECT-RELATIONAL DBMSs

187

and State levels in Figure 1. Hierarchies can express

different structures according to an analysis criterion,

e.g., geographical location. To differentiate them, the

criterion name is used, e.g., Geo location in Figure 1.

Given two consecutive levels of a hierarchy, one

is called child and the other parent depending on

whether they include more detailed or more general

data, respectively. In Figure 1, County is a child level

while State is a parent level. A level of a hierarchy

that does not have a child level is called leaf.

The relationships between child and parent lev-

els are characterized by cardinalities. In Figure 1,

the cardinality between the County and State levels

is many-to-one indicating that a county can belong to

only one state and a state can include many counties.

In a spatial hierarchy, two consecutive spatial lev-

els are related through a topological relationship. This

is represented using the pictograms of Figure 2 b).

By default the within topological relationship is con-

sidered, which indicates that the geometry of a child

member is included in the geometry of a parent mem-

ber, e.g., in Figure 1, the geometry of each county is

included in the geometry of its corresponding state.

A fact relationship (e.g., Highway maintenance

in Figure 1) represents an n-ary relationship between

leaf levels. This fact relationship can be spatial if at

least two leaf levels are spatial, e.g., the Highway seg-

ment and the County spatial levels. A spatial fact rela-

tionship may require the inclusion of a spatial predi-

cate for spatial join operations. For example, in the

ﬁgure an intersection topological relationship indi-

cates that users require to focus their analysis on those

highway segments that intersect counties.

A (spatial) fact relationship may include thematic

or spatial measures. The former are usually numeric

values that allow to perform quantitative analysis.

Spatial measures can be represented by a geometry

or calculated using spatial operators, e.g., distance,

area. The schema in Figure 1 contains two spatial

measures: Length and Common area. Length is a

number representing the length of the part of a high-

way segment that belongs to a county. Common area

represents the geometry of the common part.

3.2 Topological Constraints between

Spatial Hierarchy Levels

As was already said, in our model the default topo-

logical relationship between two consecutive spatial

levels is within. However, in real-world situations

these relationships can be different. For example, in

a spatial hierarchy formed by the Store and the City

levels, some points referring to store locations can be

on the border between two cities represented as sur-

faces. This situation may lead to the problem of mea-

sure aggregation when traversing from the Store to the

City levels since it is not clear whether the measure

(e.g., required taxes) should be distributed between

two cities or considered only for one of them.

For non-spatial hierarchies, summarizability con-

ditions were established (Lenz and Shoshani, 1997).

Summarizability refers to the correct aggregation of

measures in a higher hierarchy level (e.g., State

in Figure 1) taking into account existing aggrega-

tions in a lower hierarchy level (e.g., County in Fig-

ure 1). Nevertheless, summarizability problems may

also arise depending on the topological relationships

existing between spatial levels. Several solutions may

be applied: an extreme one is to disallow the topologi-

cal relationships that cause problems whereas another

solution is to deﬁne customized procedures for ensur-

ing correct measure aggregation.

Topological

relationship

Total containment Equal Connected

Disjoint

disjoint

within

touches crosses

overlaps

equal

Forbidden

Safe aggregation

Special aggregation

procedure

Figure 3: Classiﬁcation of topological relationships for ag-

gregation procedures.

In (Malinowski and Zim

anyi, 2005) we classi-

ﬁed topological relationships according to the re-

quired procedures for measure aggregation. Next, we

brieﬂy refer to this classiﬁcation (Figure 3), which is

based on the intersection between the geometric union

of the spatial extents of child members (denoted by

GU(C

ext

)) and the spatial extent of their associated

parent member (denoted by P

ext

The disjoint topological relationship is not al-

lowed between spatial hierarchy levels since during

a roll-up operation the next hierarchy level cannot

be reached. Thus, a non-empty intersection between

GU(C

ext

) and P

ext

is required. If GU(C

ext

) within P

ext

then the geometric union of the child member extents

(as well as the extent of each child member) is in-

cluded in their parent member extent. In this case,

the aggregation of measures from a child to a parent

level can be done safely using a traditional approach.

Similar situation occurs if GU(C

ext

) equals P

ext

In the case when the topological relationships be-

tween extents of the child and parent members are

distinct from within or equal, the topological relation-

ships between the spatial extents of every individual

child member and its parent member should be re-

vised. They allow to determine which measure values

ICEIS 2007 - International Conference on Enterprise Information Systems

188

can be considered in its entirety for aggregation and

which must be partitioned.

4 IMPLEMENTATION OF

SPATIAL HIERARCHIES

Conceptual models facilitate the representation of the

semantics of the modeled reality. However, much of

this semantics may be lost when translating a con-

ceptual schema into a logical and a physical schemas

since only the concepts supported by the target DBMS

can be used. To ensure the semantic equivalence

between these schemas, integrity constraints should

be introduced. Current DBMSs provide support for

declarative integrity constraints, such as keys, ref-

erential integrity, or check constraints. However, in

many cases this support is not sufﬁcient and integrity

constraints must be implemented using triggers. The

latter are named Event–Condition–Action rules that

are automatically activated when a table is updated.

Further, to ensure better performance during join

operations and independency from transactional sys-

tems, we choose a surrogate-based OR model. Surro-

gates are system-generated keys that cannot be seen

or modiﬁed by users. In Oracle 10g, to ensure the

existence of surrogates, an object table must be cre-

ated. It is similar to a conventional relational table

with the difference that column types correspond to

the attributes of the object type used for the table dec-

laration. Object types are types structured by users for

representing real-world objects.

Currently, several DBMSs, e.g., Oracle or In-

formix, provide extensions to deﬁne and manipulate

spatial elements. For example, Oracle 10g Spatial

allows to represent geometries using basic geomet-

ric types, such as point, line string, and polygon, or

combination of them. Oracle also extends SQL with

spatial operators and functions.

To implement spatial hierarchies, we ﬁrst, refer to

spatial levels and then, to relationships between them.

4.1 Spatial Levels

In the MultiDimER model, a level corresponds to an

entity type in the ER model. Therefore, it can be

transformed to a table in the OR model. The spatial

support in the model is added in an implicit manner,

i.e., the attribute representing the geometry is repre-

sented by pictogram. Therefore, the transformation

of a spatial level into the OR representation requires

an additional attribute for representing its geometry.

The deﬁnition of a table in Oracle 10g Spatial for

representing the State level is given next. To ensure

the existence of surrogates for the State level, ﬁrst a

object type must be deﬁned:

create type StateType as object (

Geometry mdsys.sdo geometry,

Name varchar2(25), Population number(10),

Area number, MajorActivity varchar2(50),

Capital varchar2(25));

create table State of StateType (

constraint statePK primary key (Name))

object identiﬁer is system generated;

The clause object identiﬁer is system generated indi-

cates that a surrogate attribute is automatically gener-

ated by the system (the default option).

The OR model of Oracle Spatial provides a unique

spatial data type mdsys.sdo geometry that allows to

capture locations and shapes of spatial objects. In the

example, the attribute Geometry is used for represent-

ing the geometry of a state. The speciﬁc geometry

(e.g., point or line) is deﬁned and instantiated during

an insert operation.

When the spatial types deﬁned in the conceptual

schema (e.g., surface bag for the State level in Fig-

ure 1) are transformed into Oracle Spatial, the seman-

tics may be lost. This may cause that users insert a

spatial data type different from the one that is spec-

iﬁed in the conceptual schema. Therefore, to ensure

the equivalence for spatial types between the concep-

tual and the physical schemas, a check constraint may

be suitable: alter table State add constraint ValidGeom

check (Geometry.get gtype() = 7); it enforces the ge-

ometries of a state to be of the type multipolygon

(type 7). However, Oracle does not allow such con-

structs, thus a trigger must be deﬁned:

create or replace trigger ValidGeomState

before insert or update on State for each row

begin if :new.Geometry.get gtype() <> 7 then

raise application error(-2003,’Invalid Geometry’);

end if;

end;

4.2 Relationship between Spatial Levels

A relationship between levels forming a hierarchy

corresponds to a binary relationship in the ER model.

Therefore, this relationship can be represented in the

OR model using the traditional mapping for the bi-

nary many-to-one relationships. This requires to in-

clude in the table created for the child level an at-

tribute for representing a parent key.

Figure 1 includes the Geo location spatial hier-

archy that contains the County and the State levels.

Since we already have created a table for the State

level, next we deﬁne a table for the County level:

create type CountyType as object (

IMPLEMENTING SPATIAL DATAWAREHOUSE HIERARCHIES IN OBJECT-RELATIONAL DBMSs

189

Geometry mdsys.sdo geometry,

Name varchar2(25), Population number(10),

Area number, StateRef ref StateType);

create table County of CountyType (

StateRef NOT NULL,

constraint CountyPK primary key (Name),

constraint CountyFK foreign key (StateRef)

references State);

The CountyType object includes a reference (ref) type

that points to the corresponding row in the State ta-

ble. In this way, the OR approach replaces value-

based joins with direct access to related rows using

the identiﬁers. Further, not allowing the attribute

StateRef to have null values and enforcing referential

integrity constrains ensure that every county member

has assigned a valid state member. However, to in-

sert data into the County table, the surrogates of the

corresponding state members should be known. To

facilitate this operation we create a view allowing to

introduce a state name instead of a state surrogate:

create view CountyView (Geometry, Name,

Population, Area, StateName) as

select C.Geometry, C.Name,

C.Population, C.Area, S.Name

from County C, State S

where C.StateRef = ref(S);

Since views deﬁned on two tables cannot be up-

dated, to insert data into the County table using the

CountyView, an instead of trigger should be created;

it performs actions instead of the operation speciﬁed

in the trigger.

Further, topological relationships between spatial

levels forming a hierarchy should also be considered

during implementation for preventing the inclusion of

incorrect data and for indicating what kind of aggre-

gation procedures should be developed. Two solu-

tions can be proposed: (1) constraint the geometry of

the child member during the insert operation or (2)

verify topological relationships between the geomet-

ric union of the spatial extents of child members and

the spatial extent of their associated parent member,

after the insertion of all child members.

The ﬁrst solution requires the veriﬁcation of the

topological relationship between spatial extents of a

county and a state members:

create or replace trigger CountySpaIns instead of

insert on CountySpaView for each row

declare StGeometry State.Geometry%Type;

begin select S.Geometry into StGeometry

from State S where S.Name = :new.StateName;

if SQL%found then

if sdo geom.relate(StGeometry,’anyinteract’,

:new.Geometry,0.005) = ’TRUE’ then

insert into County select :new.Geometry,

:new.Name, :new.Population; :new.Area, ref(S)

from State S where S.name = :new.StateName;

else raise application error(-2002, ’Invalid

Top. Rel.’); end if;

else raise raise application error(-2000,

’Invalid State Name: ’ || :new.StateName); end if;

end;

The trigger raises errors if the state name is invalid or

if the geometry of a county member is disjoint from

the geometry of its corresponding state member. Oth-

erwise, it inserts the new data into the County table.

In the example, to check topological relationships we

use the sdo geom.relate function with an ’anyinteract’

mask, which accepts any topological relationships but

disjoint between child and parent members. However,

a speciﬁc topological relationship can be used instead

of anyinteract, e.g., covers.

In the second solution we allow to include child

members without activating an instead of trigger. Af-

ter all child members are inserted, the veriﬁcation

of the topological relationship between the geomet-

ric union of the spatial extents of child members and

the spatial extent of their associated parent member is

performed. An example of this veriﬁcation is given

next. First, we deﬁne a function that receives a state

name and returns 1 if the spatial extent of a given

State member is equal to the geometric union of the

spatial extents of its County members:

create or replace function ChildrenWithinParent

(StateName State.Name%Type) return Number is

StName State.Name%type;

begin select S1.Name into StName

from State S1, (select S2.Name as SName,

sdo aggr union(sdoaggrtype(C.Geometry, 0.005))

as Geometry from County C , State S2

where C.StateRef = ref(S2)

group by S2.Name ) GU

where S1.Name = StateName and GU.SName =

S1.Name and sdo geom.relate(S1.Geometry, ’equal’,

GU.Geometry, 0.005)= ’equal’;

if SQL%found then return 1; else return 0; end if;

end;

We use the sdo aggr union function, which returns a

spatial object represented as the geometric union of

the speciﬁed spatial objects, e.g., county members.

This function works similarly to the aggregate func-

tions used for non-spatial data, i.e., when the group by

clause is included and the speciﬁc function is selected

(e.g., sum) with the difference that it refers to spatial

data. The select statement in the from clause, creates

a temporary table GU with two attributes SName and

Geometry. The latter is the geometric union of coun-

ties grouped by a state name. Then, this table is used

in the second

where

statement for testing the

equal

ICEIS 2007 - International Conference on Enterprise Information Systems

190

topological relationship.

The ChildrenWithinParent function can be called

for a speciﬁc state or for all states. Next, we show an

example of this call displaying a message instead of

taking some speciﬁc action:

declare StName State.Name%type;

cursor RetrieveState is

select S.Name from State S;

begin open RetrieveState;

loop fetch RetrieveState into StName;

exit when RetrieveState%notfound;

if (ChildrenWithinParent (StName) = 1) then

dbms output.put line(StName ||

’ is totally covered by its counties’);

else dbms output.put line(StName ||

’ is not totally covered by its counties’);

end if; end loop;

close RetrieveState;

end;

Since the branch else indicates that some (or all)

counties intersect their state member

, we must

check the topological relationships of individual child

members. These topological relationships can be

easily retrieved in Oracle using, e.g., the follow-

ing function for a state member S in the State

table and every related child member C in the

County table: sdo geom.relate(S.Geometry, ’deter-

mine’, C.Geometry, 0.005). Based on that and accord-

ing to user requirements, an appropriate aggregation

procedure can be developed.

5 CONCLUSIONS

The MultiDimER model provides the multidimen-

sional view of data and allows spatial support in lev-

els, hierarchies, fact relationships, and measures. In

particular, spatial hierarchies are important since they

allow to see detailed and aggregated measures while

traversing different levels. However, to ensure cor-

rect measure aggregation, topological relationships

between spatial hierarchy levels must be considered.

Furthermore, even though the model captures

users’ requirements for SDW applications, the result-

ing conceptual schemas must be translated to speciﬁc

implementation platforms (DBMSs). However, the

semantics can be lost during this translation process

due to limited expression power of current DBMSs.

This paper presented a transformation of spatial

hierarchies to the OR implementation model using as

an example Oracle 10g with its spatial extension. We

In a real situation, counties are included in states, i.e.,

this topological relationship is equal, however we use the

same example to shorten the paper’s size.

also referred to integrity constraints that allow to pre-

serve the semantics of a more expressive conceptual

schema while transforming to a physical schema.

The proposed mappings to the OR model along

with the examples using a commercial system, show

the applicability of the given solutions in real-world

situations and the feasibility of implementing SDWs

in current commercial DBMSs.

REFERENCES

Bimonte, S., Tchounikine, A., and Miquel, M. (2005). To-

wards a spatial multidimensional model. In Proc. of

the 8th ACM Int. Workshop on Data Warehousing and

OLAP, pages 39–46.

Fidalgo, R., Times, V., Silva, J., and Souza, F. (2004).

GeoDWFrame: A framework for guiding the design

of geographical dimensional schemes. In Proc. of the

6th Int Conf. on Data Warehousing and Knowledge

Discovery, pages 26–37.

Han, J., Koperski, K., and Stefanovic, N. (1997). Ge-

oMiner: a system prototype for spatial data mining.

In Proc. of the ACM SIGMOD Int. Conf. on Manage-

ment of Data, pages 553–556.

Jensen, C., Klygis, A., Pedersen, T., and Timko, I. (2004).

Multidimensional data modeling for location-based

services. VLDB Journal, 13(1):1–21.

Lenz, H. and Shoshani, A. (1997). Summarizability in

OLAP and statistical databases. In Proc. of the 9th

Int. Conf. on Scientiﬁc and Statistical Database Man-

agement, pages 132–143.

Malinowski, E. and Zim

anyi, E. (2004). Representing spa-

tiality in a conceptual multidimensional model. In

Proc. of the 12th ACM Symposium on Advances in Ge-

ographic Information Systems, pages 12–21.

Malinowski, E. and Zim

anyi, E. (2005). Spatial hierar-

chies and topological relationships in the Spatial Mul-

tiDimER model. In Proc. of the 22nd British Nat.

Conf. on Databases, pages 17–28.

Pedersen, T., Jensen, C., and Dyreson., C. (2001). A foun-

dation for capturing and querying complex multidi-

mensional data. Information Systems, 26(5):383–423.

Pedersen, T. and Tryfona, N. (2001). Pre-aggregation in

spatial data warehouses. In Proc. of the 7th Int.

Symposium on Advances in Spatial and Temporal

Databases, pages 460–478.

Rivest, S., B

edard, Y., and Marchand, P. (2001). Toward

better suppport for spatial decision making: Deﬁn-

ing the characteristics of spatial on-line analytical pro-

cessing (SOLAP). Geomatica, 55(4):539–555.

Shekhar, S. and Chawla, S. (2003). Spatial Databases: A

Tour. Prentice Hall.

Stefanovic, N., Han, J., and Koperski, K. (2000). Object-

based selective materialization for efﬁcient implemen-

tation of spatial data cubes. TKDE, 12(6):938–958.

IMPLEMENTING SPATIAL DATAWAREHOUSE HIERARCHIES IN OBJECT-RELATIONAL DBMSs

191