
MODELLING HUMAN REASONING
IN INTELLIGENT DECISION SUPPORT SYSTEMS
V. N. Vagin and A. P. Yeremeyev
Moscow Power Engineering Institute
Krasnokazarmennaya 14, 111250, Moscow, Russia
Keywords: Reasoning by analogy, intelligent decision support system, structural analogy, generalization, rough set.
Abstract: Methods of analogy-based solution searches in intelligent decision support systems are considered. The
special attention is drawn to methods based on a structural analogy that use the analogy of properties and
relations and take the context into account. Besides the problem of concept generalization is viewed. Several
algorithms based on the rough set theory are compared and the possibility to use them for generalization of
data stored in real-world databases is tested.
1 INTRODUCTION
Investigation of mechanisms that are involved in the
analogous reasoning process is an important
problem both for psychologists and specialists in
artificial intelligence (AI). The analogy can be used
in various applications of AI and for solving various
problems, e.g., for generation of hypotheses about an
unknown problem domain or for generalizing
experience in the form of an abstract scheme. The
great interest in this problem is caused by the
necessity of modelling human reasoning (common
sense reasoning) in AI systems and, in particular, in
intelligent decision support systems (IDSS).
In the encyclopaedia the word analogy (analogia,
Greek: correspondence, similarity, likeness,
closeness) is defined as the similarity of objects
(phenomena, processes) with respect to some
properties. Reasoning by analogy is the transfer of
knowledge obtained from an object to a less studied
one which is similar to the latter with respect to
some essential properties or attributes. Reasoning of
this kind is a source of scientific hypotheses.
Thus, analogy-based reasoning can be defined
as a method that allows to understand a situation
when compared with another one. In other words, an
analogy is an inference method that allows to detect
likeness between several given objects due to
transfer of facts and knowledge valid for both
objects, to other objects and to determine means of
problem solution or to forecast unknown properties.
It is this type of inference that is used by a human in
the first stages of solving a new problem. At the
present time, there are a great number of various
models, schemes, and methods that describe
mechanisms of reasoning by analogy. Another
important problem is a problem of concept
generalization especially in case it is necessary to
treat incomplete and inconsistent information.
However the real data bases (DB) contain, as a rule,
“raw” data and without analysis and generalization
these flows of “raw” data are of no use.
The common point of these data is that they
contain a large number of hidden regularities. At
present, to reveal these regularities and construct
inductive models, generalization methods and
computer systems that implement these methods are
being developed. Using generalization methods in
decision-making systems, the features that
characterize the group to which one or another
object belongs are selected. This is achieved by
analyzing already classified objects and forming a
certain set of rules (generalized model). Then, this
generalized model can be used for recognizing
objects not known to the system in advance. The
problem of classifying objects under excessive,
incomplete, or inconsistent information is very
important. We consider the opportunities of using
the rough set theory for solving problems of
inductive concept generation, as well as to propose
methods for improving known algorithms. A new
algorithm for discretization of continuous attributes
which considerably improves the efficiency of
generalization procedures is proposed. The
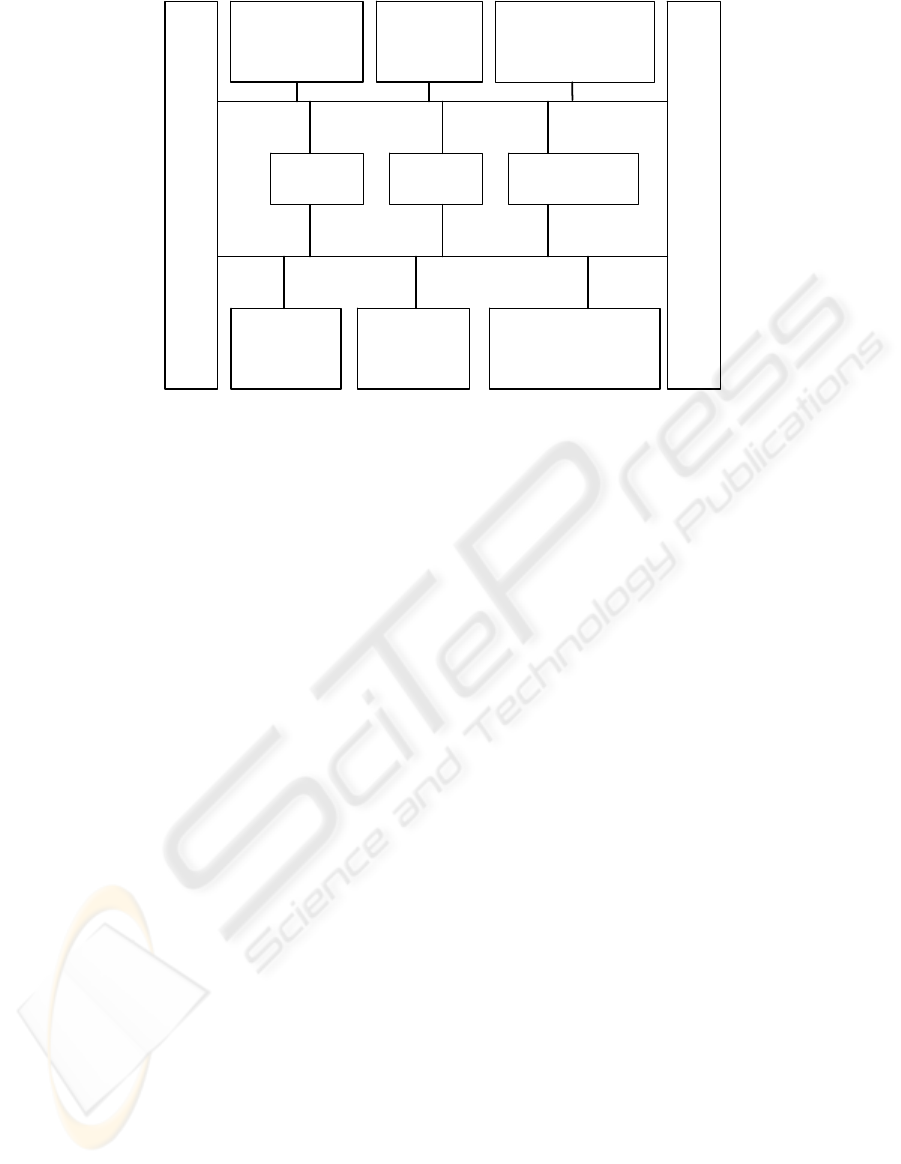
generalized structure of a real-time IDSS is given in
Fig. 1. The search for an analogous solution may be
applied in units of analysis of the problem situation,
learning, adaptation and modification, modelling,
and forecasting (Vagin, Eremeev, 2001).
277
N. Vagin V. and P. Yeremeyev A. (2007).
MODELLING HUMAN REASONING IN INTELLIGENT DECISION SUPPORT SYSTEMS.
In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 277-282
DOI: 10.5220/0002355502770282
Copyright
c
SciTePress
2 REASONING BY ANALOGY
Questions about the nature of analogies, a formal
definition, justification of reasoning by analogy, etc.,
arose in the time of epicureans and stoics. The
attempts to answer these questions, starting from the
first attempts of Leibniz to formalize this notion up
to our time, have not received a final answer
(Pospelov, 1989; Varshavskii, Eremeev, 2005).
At the present time, there are a great number of
various models, schemes, and methods that describe
mechanisms of reasoning by analogy (Varshavskii,
Eremeev, 2005; Long, Garigliano, 1994; Eremeev,
Varshavsky, 2005; Haraguchi, Arikawa, 1986).
In (Haraguchi, Arikawa, 1986), the authors have
proposed two types of analogies: an analogy for
solving problems and an analogy for forecasting.
The analogy for solving problems assumes
applying reasoning by analogy for increasing the
efficiency of the problem solution which, generally
speaking, can be solved without analogy as well, as,
e.g., in programming and proving theorems.
Analogy for prediction (forecasting) uses
reasoning by analogy for obtaining new facts. Due to
the transformation of knowledge based on the
likeness of objects, one can make the conclusion that
new facts probably hold. For example, if an analogy
is applied to a system of axioms, the result may be
certain theorems valid with respect to the system.
Here, using the similarity between axiom systems,
one can transform a theorem in a system to a logical
formula in another system and make a conclusion
that the latter is a theorem.
Depending on the nature of information
transferred from an object of analogy to the other
one, the analogy of properties and the analogy of
relations can be distinguished.
The analogy of properties considers two single
objects or a pair of sets (classes) of homogeneous
objects, and the transferred attributes are properties
of these objects, for example, analogy between
illness symptoms of two persons or analogy in the
structure of the surfaces of Earth and Mars, etc.
The analogy of relations considers pairs of
objects where the objects can be absolutely different
and the transferred attributes are properties of these
relations. For example, using the analogy of
relations, bionics studies processes in nature in order
to use the obtained knowledge in a modern
technology.
According to plausibility degrees one can
distinguish three types of analogies: strict scientific
analogies, nonstrict scientific analogies, and
nonscientific analogies.
A strict scientific analogy is applied to scientific
studies and mathematical proofs. For example, the
formulation of the attributes of the similarity of
triangles is based on a strict analogy which results in
a deductive inference, i.e., which deduces a valid
conclusion.
Unlike the strict analogy, a nonstrict scientific
analogy results only in plausible (probable)
reasoning. If the probability of a false statement is
taken equal to 0 and that of the true statement is
taken equal to 1, then the probability of inference by
a nonstrict analogy lies in the interval from 0 to 1.
To increase this probability, one needs to satisfy a
number of requirements to the method of reasoning
by analogy, otherwise, a nonstrict analogy may
become nonscientific.
A nonscientific analogy is often used
deliberately to perplex the opponent. Sometimes, a
BLOCK OF TRAINING,
ADAPTATION AND
MODIFICATION
DATA
BASE
MODEL
BASE
KNOWLEDGE
BASE
SIMULATION
BLOCK
PREDICTION
BLOCK
KNOWLEGE
ASQUISITION AND
ACCUMULATION BLOCK
USER INTERFACE (DECISION-MAKER)
OUTDOOR ENVIROMENT INTERFACE (OBJECT, DBMS etc.)
PROBLEM
SITUATION
ANALYZER
DECISION
MAKING
BLOCK
Figure 1: The generalized structure of a real-time IDSS.
ICEIS 2007 - International Conference on Enterprise Information Systems
278
nonscientific analogy is used unintentionally, by
someone not knowing the rules of analogies or
having no factual knowledge concerning the objects
and their properties that underlie the inference.
We consider the methods of solution search on
the basis of structural analogy which allows to take
into account a context and based on the theory of
structural mapping. We use semantic networks
(SNs) as a model of knowledge representation.
3 REASONING BY STRUCTURAL
ANALOGY TAKING INTO
ACCOUNT A CONTEXT
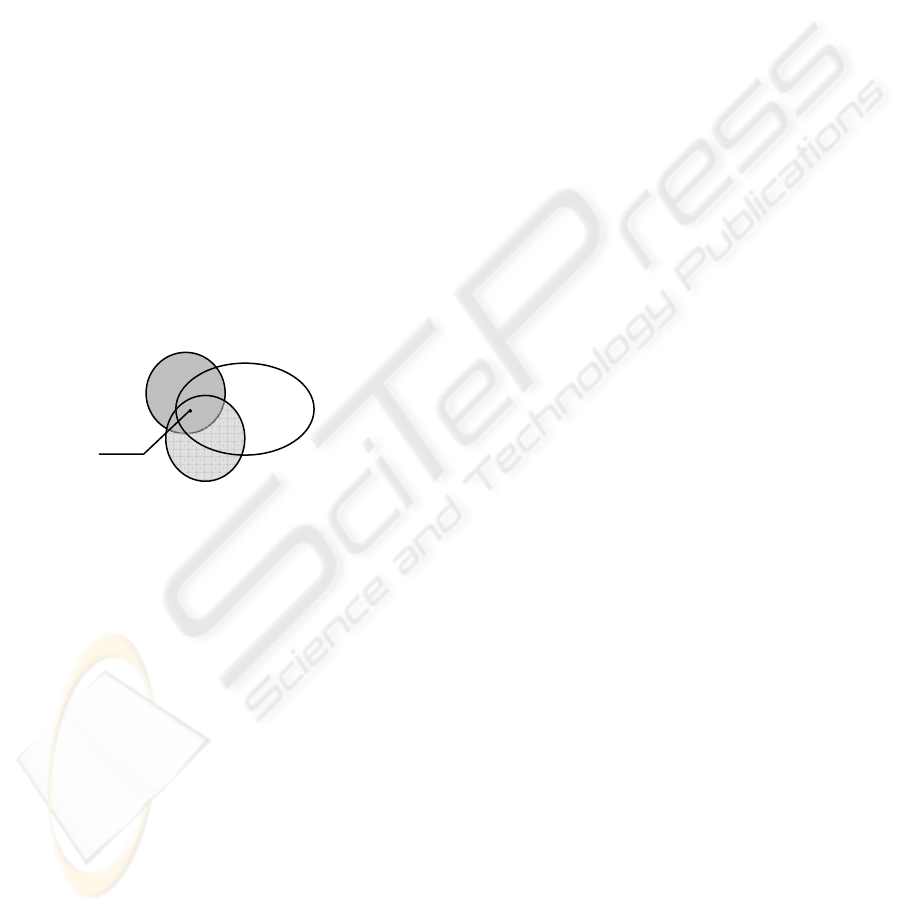
In (Long, Garigliano, 1994), the authors have
proposed to consider an analogy as a quadruple
A = <O, C, R, P> where O and R are the source
object and the receiver one and C is the intersection
object, i.e., the object that structurally intersects
them and has larger cardinality of a set of properties
as compared with these objects. In other words, the
analogy between the source object and the receiver
object is considered in the context of the
intersection, and P is a property for definition of the
original context. The structure of this analogy is
represented in Fig. 2.
Using the described structure of the analogy, the
authors of (Long, Garigliano, 1994) have proposed
the algorithm for the problem solution that is based
on analogy of the properties. A SN with information
about the problem domain, a receiver R, and a
property for defining the original context P provide
input data for this algorithm.
The algorithm for the problem solution on the
basis of analogy taking into account the context
consists of the following steps.
Step 1. Determine all objects of the SN, except
for receiver R, that have property P. If there are no
objects of this kind, then the search for a solution
fails, otherwise, go to step 2.
Step 2. For the objects found in step 1,
determine all possible intersections of C with R
taking into account P. If there are no intersections of
C, then the search for a solution fails, otherwise, go
to step 3.
Step 3. From the objects extracted in step 1,
determine all possible sources O for analogies with
the receiver R and the intersection C taking into
account P. In the case of success (possible analogies
for R are defined), go to step 4, otherwise, the search
for a solution fails.
Step 4. From the analogies extracted in step 3,
choose the most appropriate (taking into account the
requirements of the decision making person (DMP)).
In the case of success, go to step 5; otherwise, the
search for a solution fails.
Step 5. The analogies obtained in step 4 are
given to the DMP which means successful
termination of the algorithm.
Having obtained analogies, the DMP may then
make the final choice of the best ones. On the basis
of these facts, the facts (properties) that hold for the
source O are transferred to the receiver R.
Consider the modified algorithm for a problem
solution that uses the structural analogy based on the
modified structure of analogy and the algorithm for
the search of minimal intersections (Varshavskii,
Eremeev, 2005). The modification consists in the
fact that P is considered not as a unique property,
but as a set of properties that determine the original
context of the analogy. As compared with the base
variant, one of the main advantages of this modified
algorithm is the possibility of implementing the
search for a solution on the basis of analogy without
refining the original context, since in the result of
the search for the minimal intersection, one can
easily distinguish all possible contexts for the
analogy. Another important advantage of the
modified algorithm is the possibility of a more
detailed refinement of the original context for the
determination of analogies. Moreover, in the
modified algorithm there is a possibility to construct
analogy taking into account the context between
well-known objects, the source and the receiver.
4 GENERALIZATION PROBLEM
For the description of an object we will use features
a
1
, a
2
, …, a
k
, which are further called attributes.
Each object x is characterized by a set of given
values of these attributes: x = {v
1
, v
2
, …, v
k
} where v
i
is a value of the i-th attribute. Such description of an
object is called feature description. For example, the
attributes may be a colour, a weight, a form, etc.
Let we have a learning set U of objects. It
contains both the positive examples (which are
concerning to interesting concept) and the negative
examples. The concept generalization problem is the
construction of the concept allowing the correct
classifying with the help of some recognizing rule
(decision rule) of all positive and negative objects of
P
O
R
С
Figure 2: The structure of the analogy.
MODELLING HUMAN REASONING IN INTELLIGENT DECISION SUPPORT SYSTEMS
279

a learning set U. Here the construction of the
concept is made on the basis of analysis of a
learning set.
Let’s introduce the following notions related
with the set U. Let U = {x
1
, x
2
, …, x
n
} is a non-
empty finite set of objects. A = {a
1
, a
2
, …, a
k
} is a
non-empty finite set of attributes. For each attribute
the set V
a
is defined which refers to the value set of
an attribute a. We will denote the given value of an
attribute a for an object x ∈ U by a(x). At the
decision of the generalization problem, it is often
necessary to receive the description of the concept
which is specified by a value of one of the attributes.
We will denote such attribute d and call it decision
or a decision attribute. The attributes which are
included in A are called conditional attributes. The
decision attribute can have some values though quite
often it is binary. The number of possible values of a
decision attribute d is called the rank of the decision
and is designated at r(d). We will denote the value
set of the decision by
} ..., , ,{
)(21
d
dr
dd
d
vvvV =
. The
decision attribute d is defined by the partition of U
into classes C
i
= {x ∈ U: d(x) =
d
i
v }, 1 ≤ i ≤ r(d).
Generally, the concept generated on the basis of
the learning set U is an approximation to a concept
of the set X where the closeness degree of these
concepts depends on the representativeness of a
learning set, i.e. how complete the features of set X
are expressed in it.
5 CONCEPT GENERALIZATION
METHODS BASED ON THE
THEORY OF ROUGH SETS
The rough set theory has been proposed in the
beginning of 80
th
years of the last century by the
Polish mathematician Z. Pawlak. We will consider
how the rough set theory can be used to solve
concept generalization problem – see also (Pawlak,
2002; Bazan, 1998; Vagin, Golovina, ec.,2004;
Nguyen, Nguyen, 1996). In Pawlak’s works the
concept of an information system has been
introduced. An information system is understood as
the pair S = (U,A) where U = {x
1
, x
2
, …, x
n
} is a
non-empty finite set of objects named the learning
set or universe, and A = {a
1
, a
2
, …, a
k
} is a non-
empty finite set of attributes. A decision table is an
information system of the form S = (U, A ∪ {d}),
where d ∉ A is a distinguished attribute called
decision or a decision attribute. A is a set of
conditional attributes.
Now let us consider the methods of concept
generalization using the theory of rough sets.
Generally, work of the algorithm based on the rough
set theory consists of the following steps: search of
equivalence classes of the indiscernibility relation,
search of upper and lower approximations, search of
a reduction of the decision system and constructing a
set of decision rules. Moreover, discretization is
applied to processing attributes with a continuous
domain. In the case of the incomplete or inconsistent
input information, the algorithm builds two systems
of decision rules, one of them gives the certain
classification, the second gives the possible one.
Further, we will consider the most labour-consuming
steps: search of reduction and discretization making.
5.1 The Problem of Search of
Reduction
Let’s consider the process of search of reduction
that is very important part of any method used the
rough set approach. Quite often an information
system has more than one reduction. Each of these
reductions can be used in the procedure of decision-
making instead of a full set of attributes of an
original system without a change of dependence of
the decision on conditions that is characteristic for
an original system. Therefore, the problem of a
choice of the best reduction is reasonable. The
answer depends on an optimality criterion related to
attributes. If it is possible to associate with attributes
the cost function which expresses complexity of
receiving attribute values, then the choice will be
based on the criterion of the minimal total cost. The
problem of searching for a reduction with minimal
length is NP-hard (Skowron, Rauszer, 1992).
Thus, the problem of a choice of relevant
attributes is one of the important problems of
machine learning. There are several approaches
based on the rough set theory. One of the first ideas
was to consider as the relevant attributes those
attributes which are contained in intersection of all
reductions of an information system.
Other approach is related to dynamic reductions
(Bazan, 1998), i.e. conditional attribute sets
appearing “sufficiently often” as reductions of sub-
samples of an original decision system. The
attributes belonging to the “most” of dynamic
reductions are considered as relevant. The value
thresholds for “sufficiently often” and “most” should
be chosen for given data.
The third approach is based on introduction of
the notion of significance of attributes that allows by
real values from the closed interval [0, 1] to express
how important an attribute in a decision table.
ICEIS 2007 - International Conference on Enterprise Information Systems
280
5.2 The Modification of the
Discretization Algorithm
The stage of discretization is necessary for the most
of modern algorithms for generalization. The
discretization is called a transformation of a
continuous domain of attributes in a discrete one.
For example, the body temperature of the human
being which is usually measured by real numbers
can be divided into some intervals, corresponding to
a low, normal, high and very high temperature. The
choice of suitable intervals and partition of
continuous domains of attributes is a problem whose
complexity grows in exponential dependence on the
number of attributes to which discretization should
be applied. The general approach of the most
discretization algorithms is based on that any
irreducible set of cuts of a decision table S is a
reduction of other decision table constructed on the
basis of S.
Our algorithm is directed towards decreasing
time and memory consumption. It is based on the
Jonson’s strategy and extension of idea of iterative
calculation of the number of pair of objects,
discerned by a cut. This idea has been offered in
(Nguyen, Nguyen, 1996), however, originally, it is
applicable only when some restrictions on the
decision table are imposed. This idea is based on
assumption that there is a close relation between two
consecutive cuts. So, for example, it is possible to
notice, that in each row of the table all the cells with
value 1 are placed successively within one attribute.
Therefore some pairs of objects are discerned by
both consecutive cuts, and changes in the number of
discernible pairs of objects can be only due to
objects which attribute values lay between two these
cuts. In (Nguyen, Nguyen, 1996), the situation,
when no more than one object lies in this interval, is
considered. We generalize this idea on a case of the
arbitrary number of such objects. Thus, our
algorithm extends idea of iterative calculating
number of pairs of objects discerned by a cut to an
arbitrary decision table. In the majority of the
algorithms which are based on the rough set theory
and carrying out splitting of continuous attribute
domains into finite number of intervals, the stage of
discretization is considered as preparatory before
search of significant attributes. And consequently at
a stage of discretization, there is a splitting the
domains of all continuous attributes including
insignificant. In this work, the combined
implementation of discretization with search of a
reduction is offered to make discretization only for
those quantitative attributes which appear to be
significant during search of reduction.
Thus, the developed algorithm for search of
significant attributes is based on two ideas:
1) combination of discretization of quantitative
attributes with search of significant attributes,
2) search for an approximation of reduction, but no
for reduction itself. Let’s name it as Generalized
Iterative algorithm based on the Rough Set
approach, GIRS.
5.3 Results of the Experiments
The implemented experiments have shown that the
developed algorithm allows to reduce time for
search of significant attributes essentially, due to
combination with the discretization stage and use of
the proposed algorithm.
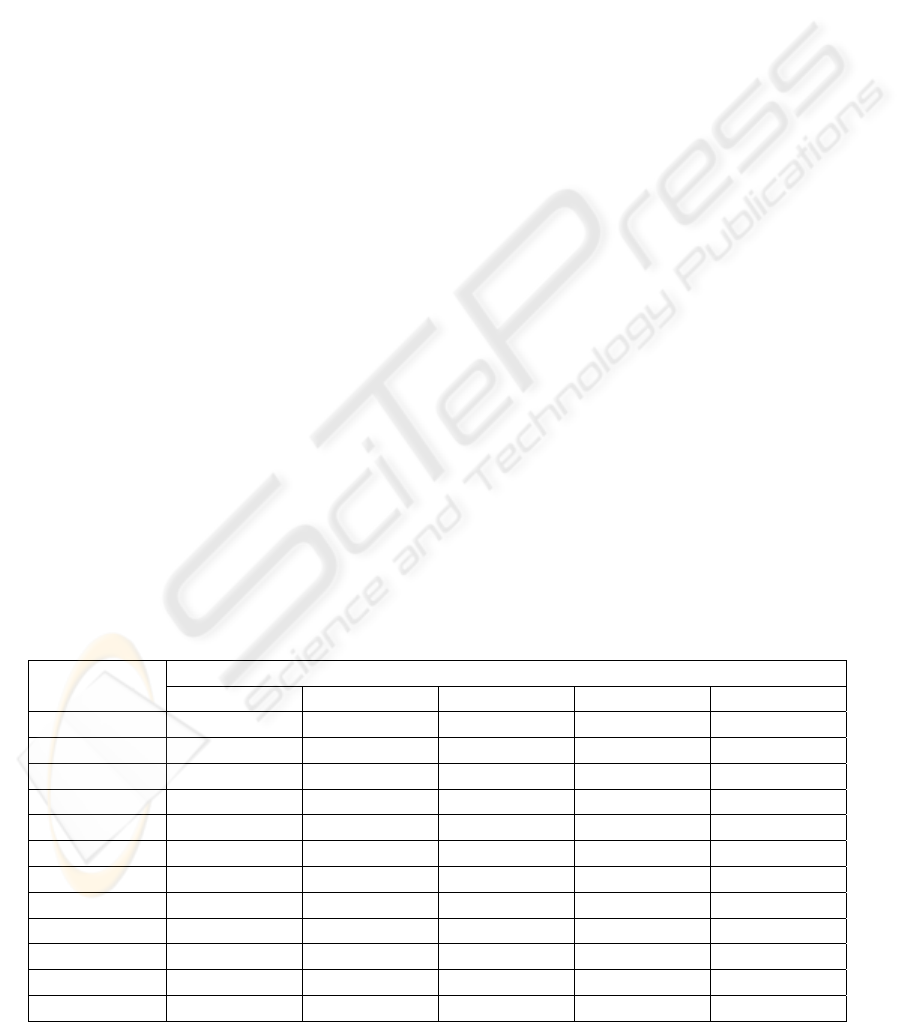
The results of the experiments executed on 11
data sets from a well known collection UCI Machine
Learning Repository (Merz, Murphy, 1998) of the
University of California are given in Table 1.
For all data sets taken into the comparison, the
Classification accuracy Data set
ID3 C4.5 MD Holte-II
GIRS
Monk-1 81.25 75.70 100 100
100
Monk-2 65.00 69.91 99.70 81.9
83.10
Monk-3 90.28 97.20 93.51 97.2
95.40
Heart 77.78 77.04 77.04 77.2
78.72
Hepatitis n/a 80.80 n/a 82.7
84.51
Diabetes 66.23 70.84 71.09 n/a
81.00
Australian 78.26 85.36 83.69 82.5
88.71
Glass 62.79 65.89 66.41 37.5
70.10
Iris 94.67 96.67 95.33 94.0
96.24
Mushroom 100 100 100 100
100
Soybean 100 95.56 100 100
100
Average 81.63 83.18 88.67 85.3
88.89
Table 1: Comparison of classification accuracy of the developed algorithm with other generalization algorithms.
MODELLING HUMAN REASONING IN INTELLIGENT DECISION SUPPORT SYSTEMS
281

developed algorithm has shown classification
accuracy that not concedes to other generalization
algorithms, and in some cases surpasses them.
Average accuracy of classification is approximately
88.9%. It is necessary to note that the classification
accuracy received by our algorithm is much above
that the classification accuracy achieved by methods
of an induction of deciding trees (ID3, ID4, ID5R,
C4.5) at the solving the majority of the problems. It
is explained by the impossibility of representation of
the description of some target concepts as a tree.
Moreover, it is possible to note that combining of
search of significant attributes and the discretization
procedure is very useful. Most clearly, it is visible
from the results received at the decision of the
Australian credit task. It is possible to explain by the
presence in these data the attributes both with
continuous and with discrete domains. The
modification of the search procedure of significant
attributes is directed namely to processing of such
combination.
6 CONCLUSIONS
The method of reasoning by analogy on the basis of
structural analogy was considered from the aspect of
its application in modern IDSS, in particular, for a
solution of problems of real-time diagnostics and
forecasting. The example of the algorithm for
solution search on the basis of analogy of properties
that takes into account the context was proposed.
This algorithm uses a modified structure of analogy
that is capable of taking into account not one
property (as in the base algorithm), but a set of
properties. These properties determine the original
context of analogy and transfer from the source to
the receiver only those facts that are relevant in the
context of the constructed analogy.
The presented method was applied at
implementation of a prototype of IDSS on the basis
of non-classical logics for monitoring and control of
complex objects like power units.
We have also considered the concept
generalization problem and the approach to its
decision based on the rough set theory. The heuristic
discretization algorithm directed towards the
decreasing of time and memory consumption has
been proposed. It is based on Jonson’s strategy and
extension of idea of iterative calculation number of
pairs of objects discerned by a cut. Also the search
algorithm of the significant attributes combined with
the stage of discretization is developed. It allows to
avoid splitting into intervals of continuous domains
of insignificant attributes.
REFERENCES
Vagin, V. N., Eremeev, A. P., 2001. Some Basic
Principles of Design of Intelligent Systems for
Supporting Real-Time Decision Making // Journal of
Computer and Systems Sciences International, v.
40(6), p.953-961.
Pospelov, D. A., 1989. Reasoning modeling. М.: Radio
and communication (in Russian).
Varshavskii, P. R., Eremeev, A.P., 2005. Analogy-Based
Search for Solutions in Intelligent Systems of Decision
Support // Journal of Computer and Systems Sciences
International, v. 44(1), p. 90–101.
Long, D., Garigliano, R., 1994. Reasoning by analogy and
causality: a model and application // Ellis Horwood
Series in Artificial Intelligence.
Eremeev, A., Varshavsky, P., 2005. Analogous Reasoning
for Intelligent Decision Support Systems //
Proceedings of the XI
th
International Conference
“Knowledge-Dialogue-Solution” – Varna, v.1, p. 272-
279.
Haraguchi, M., Arikawa, S., 1986. A Foundation of
reasoning by Analogy. Analogical Union of Logic
Programs // Proceedings of Logic Programming
Conference, Tokyo.
Pawlak, Z., 2002. Rough sets and intelligent data analysis
/ Information Sciences, Elsevier Science, November
2002, vol. 147, iss. 1, pp. 1-12.
Bazan, J., 1998. A comparison of dynamic non-dynamic
rough set methods for extraction laws from decision
tables / Rough Sets in Knowledge Discovery 1:
Methodology and Applications // Poldowski L.,
Skowron A. (Eds.), Physica-Verlag.
Vagin, V. N., Golovina, E. U., et al. Exact and plausible
inference in intellegent systems / V.N. Vagin,
D.A. Pospelov (eds), Moscow, Fizmatlit, 2004, 704 p.
(in Russian).
Nguyen, S. H., Nguyen, H. S., 1996. Some efficient
algorithms for rough set methods / Proc. of the
Conference of Information Processing and
Management of Uncertainty in Knowledge-Based
Systems, Spain, pp. 1451-1456.
Skowron, A., Rauszer, C., 1992. The Discernibility
Matrices and Functions in Information Systems /
Intelligent Decision Support – Handbook of
Applications and Advances of the Rough Sets Theory,
Kluwer, pp. 331-362.
Merz, C. J., Murphy, P.M., 1998. UCI Repository of
Machine Learning Datasets. Information and Compu-
ter Science University of California, Irvine, CA,
http://www.ics.uci.edu/~mlearn/MLRepository.html.
ICEIS 2007 - International Conference on Enterprise Information Systems
282
