FORECASTING OF CHANGES OF COMPANIES FINANCIAL

STANDINGS ON THE BASIS OF SELF-ORGANIZING MAPS

Egidijus Merkevičius, Gintautas Garšva, Stasys Girdzijauskas

Department of Informatics, Kaunas Faculty of Humanities, Vilnius University, Muitinės st. 8, LT- 44280 Kaunas, Lithuania

Vitolis Sekliuckis

Department of Software Engineering, Kaunas University of Technology, Studentų 50, LT-51368 Kaunas, Lithuania

Keywords: Bankruptcy, Self-organizing maps, Neural network, prediction, multivariate discriminate model.

Abstract: The multivariate discriminate models have been used in area of bankruptcy analysis for many years. In this

paper we suggest to conjunct the principles of traditional discriminate bankruptcy models with modern

methods of machine learning. We propose the forecasting model based on Self-organizing maps, where

inputs are indicators of multivariate discriminate model. Accuracy of forecasting is improved via changing

weights with supervised learning type ANN. We’ve presented results of testing of this model in various

aspects.

1 INTRODUCTION

The multivariate discriminate models such a Altman

Z-score (1968, 2001), Zmijewski (1984), or

Shumway (2001) have been used in area of

bankruptcy analysis for many years. The key-point

of multivariate discriminate models is to determine

the most important indicators (ratios) and their

weights in discriminate or logistic function.

Starting 80`s the artificial intelligence methods,

for example, artificial neural networks (ANN), fuzzy

logic, expert systems, have been developed and find

theoretical and practical adaptability for forecasting

of changes of companies financial standings. One of

the type of unsupervised learning ANN is Self-

organizing maps, first presented by Kohonen

(Kohonen, 1997).

In this paper, we suggest to conjunct the

principles of traditional discriminate bankruptcy

models with modern methods of machine learning.

We propose the forecasting model based on Self-

organizing maps, where inputs are indicators of

multivariate discriminate model. Accuracy of

forecasting is improved via changing weights with

supervised learning type ANN.

Review of related works in the adaptability of

SOM for finance related problems is presented in the

second section of this paper. The basic principles of

proposed Neuro-discriminate model are presented in

the third section. The results of experiments with

proposed model using the real world financial data

are demonstrated in the forth section. The last

section makes some conclusions and introduces

future works.

2 RELATED WORKS

A detailed description of the SOM method is

presented in (Kohonen, 1997). Martin-del-Prio and

Serrano-Cinca were one of the first who applied

SOM in financial analysis. They generated SOM’s

of Spanish banks and subdivided those banks into

two large groups. The configuration of banks

allowed determining root causes of the banking

crisis (Martin-del-Prio and Serrano-Cinca, 1993).

In this case (Merkevičius et.al, 2006) the

bankruptcy class of data is labeled on the map and

the data distribution is analyzed.

Kiviluoto (Kiviluoto, 1998) made a map by

means of including 1137 companies, 304 out of

which were crashed. It was stated that SOM’s give

useful qualitative information for establishing

similar input vectors. Based on Kiviluoto’s study,

through visual exploration one can see the

416

Merkevi

cius E., Garšva G., Girdzijauskas S. and Sekliuckis V. (2007).

FORECASTING OF CHANGES OF COMPANIES FINANCIAL STANDINGS ON THE BASIS OF SELF-ORGANIZING MAPS.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 416-419

DOI: 10.5220/0002371804160419

 SciTePress

distribution of important indicators (i.e. bankruptcy)

on the map.

3 METHODOLOGY

Artificial neural networks (ANN) are divided into

supervised and unsupervised learning (Atiya, 2001,

Vesanto et.al, 2000). The Self-organizing map

(SOM) is an unsupervised learning artificial neural

network that is generated without defining output

values (Doebeck, 1998). The outcome of this

process is a two-dimensional cluster map that can

visually demonstrate the financial units which are

scattered according to similar characteristics.

Methods used in the Model are original with no

major adjustments, so they are not presented. More

detailed description of multivariate discriminate

analysis, supervised learning neural network and

self-organizing maps are presented in (Altman,

1968, Zmijewski, 1984, Kohonen, 1997, Atiya,

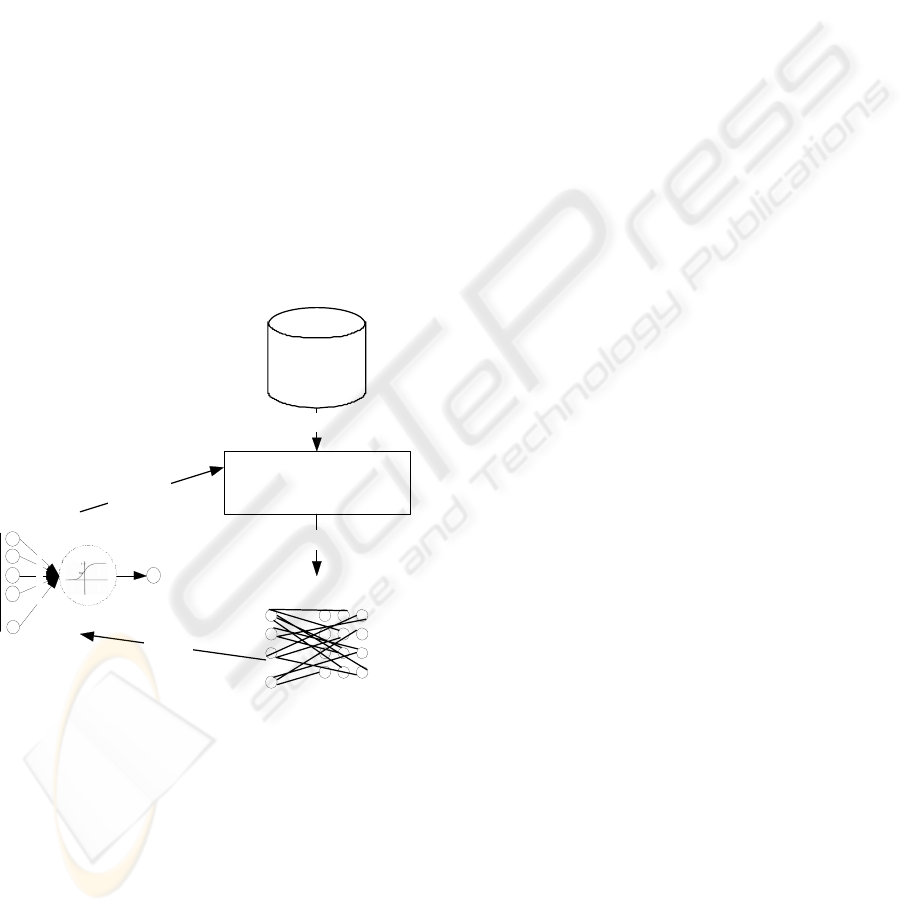
2001). Figure 1 shows the concept of the model.

Financial data

Multivariate discriminate

bankruptcy model

data

inputs / outputs

we i g h t s

corrected

we i ght s

FF ANN

...

SOM

Figure 1: The concept of the model.

A description of the Model concept is as follows:

1) Changes of companies financial standing are

determined as changes of the indexes of

bankruptcy model during two periods straight

(0 – negative changes, 1 – positive changes);

2) The components of discriminate bankruptcy

model are used for training of unsupervised

neural network and generating SOM. Testing

of accuracy of the SOM is executed via

calculation of corresponding nodes between

training and testing data.

3) The accuracy of forecasting is improved via

changing of weights. Feed-forward neural

network (further - FF ANN) is used in the

Model as a tool for changing of weights. The

main principle is taken from the core of ANN

theory – training an ANN the weights in the

ANN are adjusted while the ANN gives the

same outputs as in the training data. In other

words, the goal of the ANN is to get optimal

set of weights via changing them. In that way

the inputs of FF ANN would be data of testing

and the outputs would be the original

generated labels of SOM nodes. Initial

weights in the ANN are set as weights of

original bankruptcy model as described above.

4 RESULTS OF TESTING

The testing of proposed Model has been executed

using real financial dataset: companies from

NASDAQ list loaded from EDGAR PRO Online

database (EDGAR Pro Online, 2007). The basic

characteristics of the dataset and the experiments are

as follows:

 Number of companies: 9364.

 Dataset consists of annual financial statements

of 7 periods consecutively. The dataset was

rebuilt in the way that the string of record was

a pair of financial statement straight. After

that count of records seeks 56184 records.

 Count of records was reduced to 46353 records

after elimination of missing data.

 Records are divided to the two subsets – the

one for the training (TRAINDATA), the

second – for the testing (TESTDATA). On the

each iteration, the separation of data into the

training and testing data has been executed

randomly with the ratio 70:30.

 Risk classes of bankruptcy are determined as

follows: if the index of selected bankruptcy

model – in this case – Zmijewski bankruptcy

model (Zmijewski, 1984) - of the second

period is less than index of the first period

then the risk class is determined as 0,

otherwise – 1.

 According to Zmijewski`s model, there are 3

variables (inputs) for each of 2 periods for the

training of SOM:

o p0w2 and p1w2: Net income/Total assets

(original weight is -4.513),

o p0w3 and p1w3: Total liabilities/Total

assets (5.679)

FORECASTING OF CHANGES OF COMPANIES FINANCIAL STANDINGS ON THE BASIS OF

SELF-ORGANIZING MAPS

417

o p0w4 and p1w4: Short-term assets/ Short-

term liabilities (0.004).

The main principle of the measurement of

prediction accuracy is as follows: the labeled nodes

of trained SOM are labeled with the outputs of

testing data and the corresponding nodes of training

and testing data are calculated.

First stage of experiments is related with the

determination of the optimal structure of SOM. We

have executed the cycle of training/testing

repeatedly increasing the number of SOM nodes.

The result of prediction accuracy is showed in the

figure 2.

Figure 2: The result of prediction accuracy changing

number of nodes.

We can see that the best performance of accuracy

(~78%) is reached when the number of SOM nodes

is app. 1200.

Second stage of testing of model is to improve

the accuracy with the ANN. As a result, we get

changed weights according to the labels of generated

SOM. These weights participate in the further stages

of the cycle as described above in the section 3 and

showed above in the figure 1. When the performance

of the prediction does not rapidly change, the cycle

has stopped. After 21 iterations, we have improved

accuracy of prediction from 77.78% to 92.41% as

showed in the figure 3:

Some interesting moments are remarked during

analysis of this graph:

 Accuracy of prediction increased rapidly from

77.30% to 89.86% after 5 iterations of the

cycle. Increase was influenced mainly under

changing of variable p1w4 (Short-term assets/

Short-term liabilities (0.004)) as shown in the

second graph of the figure 3 – after 6 iteration

difference between changed and original

weight (p1w4) seeks 1.071.

 After further iterations of the cycle, differences

between changed and original variables do not

increase and remains at the same level.

 We could observe an interesting case on the 27

iteration of the cycle when all aspects of

calculation of accuracy are nearly equal. Other

case shows conversely results: on the 31

iteration accuracy of ‘0’ reaches the best result

(96.96%) but accuracy of ‘1’ presents the

worst result (68.98%).

 We consider, the optimal structure of the

weights was reached after the 21 iterations.

Average of accuracy aspects calculates to

92.41%.

Table 2 presents Confusion matrix of the results

after 21 iterations.

Table 1: Confusion matrix.

Actual vs Predicted (Confusion matrix)

Predicted (by model)

0 1 Total (units)

Actual 0 (%)

95.73 4.27 866

Actual 1 (%)

12.27 87.73 277

Total accuracy (%) 93.79

Average of all aspects of accuracy (%) 92.41

Table 2 presents comparison of importance of

ratios in discriminate bankruptcy model before and

after changing of weights:

Figure 3: Improving of accuracy.

ICEIS 2007 - International Conference on Enterprise Information Systems

418

Table 2: Weights before and after improving.

Name Weights

before

Weights after

21 iterations

no-ratio weight -4,336 -4,336

Net income/Total

assets

-4,513 -4,323

Total liabilities/Total

assets

5,679 5,412

S.-t. assets/ S.-t.

liabilities

0,004 -0,276

no-ratio weight -4,336 -4,336

Net income/Total

assets

-4,513 -4,797

Total liabilities/Total

assets

5,679 5,715

S.-t. assets/ S.-t.

liabilities

0,004 -1,290

Performance of

bankruptcy

prediction (%)

77.78 92.41

Changing of weights allows seek the highest

accuracy of bankruptcy prediction

The highest impact on results has Short-term

assets/Short-term liabilities ratio – accuracy of

prediction increases rapidly due to changing of

weight of this ratio.

5 CONCLUSIONS

 The presented model for forecasting of changes

of companies financial standings on the basis

of Self-organizing maps also includes

multivariate discriminate analysis of

bankruptcy and feed-forward supervised

neural network; combination of these methods

makes original model suitable for forecasting.

 The presented model works well with real

world data, the tests of the model with

presented dataset showed accuracy of

prediction with more than 92% performance.

 Changing of weights with supervised neural

network allows seek the highest accuracy of

bankruptcy prediction.

 Changing of the weights with supervised ANN

makes assumptions which ratios have highest

impact on prediction results.

Further works in this area would bee related with

testing of other discriminate models of bankruptcy,

experiments with other datasets, comparison with

other methods of bankruptcy prediction.

REFERENCES

Atiya, A.F., 2001. Bankruptcy prediction for credit risk

using neural networks: a survey and new results. In

IEEE Transactions on Neural Networks, Vol. 12, No.

4, pp. 929-935.

Altman, E., 1968. Financial Ratios, Discrimination

Analysis and the Prediction of Corporate Bankruptcy.

Journal of Finance. pp. 589-609.

Altman, E., 2000. Predicting Financial Distress of

Companies: Revisiting the Z-Score and ZETA®

Models. Working paper at

http://pages.stern.nyu.edu/~ealtman/Zscores.pdf .

Deboeck, G., 1998. Self-Organizing Maps Facilitate

Knowledge Discovery In Finance. Financial

Engineering News.

EDGAR Online, Inc. 1995-2006. http://pro.edgar-

online.com.

Kiviluoto, K., 1998. Predicting bankruptcies with the self-

organizing map. Neurocomputing, Vol. 21.pp.191–

201.

Kohonen, T., 1997. The Self-Organizing Map. In

Proceedings of the IEEE, 78.pp.1464-1480.

Martin-del-Prio, K., Serrano-Cinca, 1993. Self-Organizing

Neural Network: The Financial State of Spanish

Companies. In Neural Networks in Finance and

Investing. Using Artificial Intelligence to Improve

Real-World Performance. R.Trippi, E.Turban, Eds.

Probus Publishing,, pp. 341-357.

Merkevičius, E., Garšva, G., Girdzijauskas, S., 2006. A

Hybrid SOM-Altman Model for Bankruptcy

Prediction. In International Conference on

Computational Science (4), Lecture Notes in

Computer Science, 3994, pp. 364-371, ISSN 0302-

9743.

Shumway, T., 2001. Forecasting Bankruptcy More

Accurately: A Simple Hazard Model, Journal of

Business, Vol. 74, No. 1, pp. 101-124.

Vesanto, J., Himberg, J., Alhoniemi, E., Parhankangas, J.,

2000. SOM toolbox for Matlab 5, Technical report

A57, Helsinki University of Technology, Finland.

Zmijewski, M.E., 1984. Methodological Issues Related to

the Estimation of Financial Distress Prediction

Models. In Journal of Accounting Research 24

(Supplement). pp. 59-82.

FORECASTING OF CHANGES OF COMPANIES FINANCIAL STANDINGS ON THE BASIS OF

SELF-ORGANIZING MAPS

419