
ONE-TO-MANY DATA TRANSFORMATION OPERATIONS
Optimization and Execution on an RDBMS
Paulo Carreira
Faculty of Sciences, University of Lisbon, C6 - Piso 3, 1749-016 Lisboa, Portugal
Helena Galhardas, Jo
˜
ao Pereira and Andrzej Wichert
INESC-ID, Avenida Prof. Cavaco Silva, Tagus Park, 2780-990, Porto-Salvo, Portugal
Keywords:
Data Warehousing, Data Cleaning, Data Integration, ETL, Query optimization.
Abstract:
The optimization capabilities of RDBMSs make them attractive for executing data transformations that support
ETL, data cleaning and integration activities. However, despite the fact that many useful data transformations
can be expressed as relational queries, an important class of data transformations that produces several output
tuples for a single input tuple cannot be expressed in that way.
To address this limitation a new operator, named data mapper, has been proposed as an extension of Re-
lational Algebra for expressing one-to-many data transformations. In this paper we study the feasibility of
implementing the mapper operator as a primitive operator on an RDBMS. Data transformations expressed as
combinations of standard relational operators and mappers can be optimized resulting in interesting perfor-
mance gains.
1 INTRODUCTION
The setup of modern information systems comprises
a number of activities that rely, to a great extent, in
the use of data transformations (Lomet and Runden-
steiner, 1999). Well known cases are the migration
of legacy data, the ETL processes that support data
warehousing, data cleaning processes and the integra-
tion of data from multiple sources.
One natural way of expressing data transforma-
tions is to use a declarative query language and to
specify the data transformations as queries (or views)
over the source data. Because of the broad adop-
tion of RDBMSs, such language is often SQL, a lan-
guage based on Relational Algebra (RA). Unfortu-
nately, due to its limited expressive power (Aho and
Ullman, 1979), RA alone cannot be used to specify
many important classes of data transformations.
An important class of data transformations that
may not be expressible in RA are the so called
one-to-many data transformations (Carreira et al.,
2006), that are characterized by producing several
output tuples for each input tuple. One-to-many data
transformations occur normally due to the existence
of data heterogeneities, i.e., due to the use of different
Relation
LOANS
Relation
PAYMENTS
ACCT AM
12 20.00
3456 140.00
901 250.00
ACCTNO AMOUNT SEQNO
0012 20.00 1
3456 100.00 1
3456 40.00 2
0901 100.00 1
0901 100.00 2
0901 50.00 3
Figure 1: Illustration of an unbounded data-transformation.
(a). The source relation
LOANS
on the left, and (b) the target
relation
PAYMENTS
on the right.
representations, of the same data of source and target
schemas (Rahm and Do, 2000). For instance, source
data may consist of salaries aggregated by year, while
the target data consists of salaries aggregated by
month. Hence, each input row has to be converted
into multiple output rows, one for each month. In
this case, each input row corresponds to at most
twelve output rows. However, expressing such data
transformations as RA expressions is hampered by
the fact such bound cannot always be established
a-priori. Consider the following example:
21
Carreira P., Galhardas H., Pereira J. and Wichert A. (2007).
ONE-TO-MANY DATA TRANSFORMATION OPERATIONS - Optimization and Execution on an RDBMS.
In Proceedings of the Ninth International Conference on Enterprise Information Systems - DISI, pages 21-27
DOI: 10.5220/0002371900210027
Copyright
c
SciTePress

EXAMPLE 1.1 Consider the source relation
LOANS
[
ACCT
,
AM
] (represented in Figure 1) that
stores the details of loans per account. Sup-
pose that
LOANS
data must be transformed into
PAYMENTS
[
ACCTNO
,
AMOUNT
,
SEQNO
], the target
relation, according to the following requirements:
1. In the target relation, all the account numbers
are left padded with zeroes. Thus, the attribute
ACCTNO
is obtained by (left) concatenating zeroes
to the value of
ACCT
.
2. The target system does not support payment
amounts greater than 100. The attribute
AMOUNT
is obtained by breaking down the value of
AM
into
multiple parcels with a maximum value of 100, in
such a way that the sum of amounts for the same
ACCTNO
is equal to the source amount for the same
account. Furthermore, the target field
SEQNO
is a
sequence number for the parcel. This sequence
number starts at 1 for each sequence of parcels of
a given account.
The implementation of data transformations sim-
ilar to those requested for producing the target rela-
tion
PAYMENTS
of Example 1.1 is challenging, since
the number of output rows, for each input row,
is determined by the value of the attribute
AM
. In
this case, the upper bound on the number of out-
put rows cannot be determined by analyzing the
data transformation specification. We designate these
data transformations as unbounded one-to-many data
transformations. Other sources of unbounded data
transformations exist like, for example, converting
collection-valued attributes of SQL:1999 (Melton and
Simon, 2002), where each element of the collection is
mapped to a new row in the target table. In the context
of data-cleaning, one commonplace transformation is
converting a list of elements encoded as a string at-
tribute.
Currently, one has to resort, either to a general
purpose programming language, to some flavor of
proprietary scripting of an ETL tool, or to an RDBMS
using recursive queries of SQL:1999 (Melton and Si-
mon, 2002), or some sort of Persistent Stored Mod-
ules (PSMs) (Garcia-Molina et al., 2002, Section 8.2)
like stored procedures or table functions (Eisenberg
et al., 2004).
To address the problem of expressing one-to-many
data transformations in a declarative and optimizeable
fashion, specialized relational operator named map-
per was recently proposed as an extension to RA with
a (Carreira et al., 2006). Informally, a mapper is ap-
plied to an input relation and produces an output re-
lation. It iterates over each input tuple and gener-
ates one or more output tuples, by applying a set of
domain-specific functions. This way, it supports the
dynamic creation of tuples based on a source tuple
contents.
Although mappers appear implicitly in systems
supporting schema and data transformations underly-
ing ETL, data cleaning and data warehousing (Gal-
hardas et al., 2000; Raman and Hellerstein, 2001; Cui
and Widom, 2001; Amer-Yahia and Cluet, 2004), as
far as we know, their execution and optimization has
never been, properly studied.
This paper studies the feasibility of extending
RDBMSs with the mapper operator. There are sev-
eral reasons to do so: First, implementing the map-
per operator as a relational operator opens interest-
ing optimization opportunities since expressions that
combine the mapper operator with standard RA oper-
ators can be optimized. Second, many data transfor-
mations are naturally expressed as relational expres-
sions, leveraging the optimization strategies already
implemented by RDBMSs (Chaudhuri, 1998). Third,
such extension further equips RDBMSs for data trans-
formation activities, broadening their applicability in
a wider range of data management activities. We re-
mark that our idea of using RDBMSs as data transfor-
mation engines is not revolutionary, see (Haas et al.,
1999). Furthermore, several RDBMSs like Microsoft
SQL Server and Oracle already include additional
software packages specific for ETL tasks.
Our contributions of are the following: (i) an
SQL-like concrete syntax for the mapper operator ac-
complished by extending the select statement, (ii) the
study of several query rewriting possibilities to be in-
corporated in the query optimizer and (iii) an exper-
imental validation of the usefulness of implementing
the mapper operator by comparing its physical imple-
mentation with alternative RDBMS solutions.
The rest of the paper is organized as follows. Sec-
tion 2 introduces the mapper operator and exposes its
concrete syntax by example. Then, in Section 3 we
discuss how to extend the query optimizer to handle
mappers. In Section 4, we report on a series of exper-
iments to ascertain the feasibility of implementing the
mapper operator and finally Section 5 concludes.
2 THE MAPPER OPERATOR
The mapper operator is formalized as a unary operator
µ
F
that takes a relation instance of the source relation
schema as input and produces a relation instance of
the target relation schema as output. The operator is
parameterized by a set F of functions, which we des-
ignate as mapper functions. The intuition is that each
mapper function f
A
i
expresses a part of the envisaged
ICEIS 2007 - International Conference on Enterprise Information Systems
22

data transformation, focused on a non-empty set A
i
of attributes of the target schema. A key insight is
that, when applied to a tuple, a mapper function can
produce a set of values in the domain of its target at-
tributes Dom(A
i
), rather than a single value. Further
details can be found in (Carreira et al., 2005b).
The mapper operator is formally defined as
follows: Given a set of mapper functions F =
{ f
A
1
,..., f
A
k
}, the mapper of a relation s with respect
to F, denoted by µ
F
(s), is the relation instance of the
target relation schema defined by
µ
F
(s)
def
= {t ∈ Dom(Y) | ∃u ∈ s s.t.
t[A
i
] ∈ f
A
i
(u), ∀1 ≤ i ≤ k}
(1)
We can express the data transformation of Ex-
ample 1.1 by means of a mapper µ
acct,amt
, compris-
ing two mapper functions. The function acct is the
mapper function that returns a singleton with the ac-
count number
ACCT
properly left padded with zeroes,
while amt is a mapper function that produces the at-
tributes
[AMOUNT,SEQNO]
, s.t., amt(am) is given by
{(100,i) | 1 ≤ i ≤ (am/100)} ∪ {(am%100, (am/100) +
1) | am%100 6= 0}, where % represents the modu-
lus operation. For instance, if v is the source tuple
(
901
,
250.00
), the result of evaluating amt(v) is the
set {(
100
,
1
),(
100
,
2
),(
50
,
3
)}. Given a source relation
s including v, the result of the expression µ
acct,amt
(s)
is another relation that contains the set of tuples
{h
’0901’
,
100
,
1
i, h
’0901’
,
100
,
2
i, h
’0901’
,
50
,
3
i}.
2.1 Concrete Syntax
The mapper operator can be easily embedded into
the SQL syntax by incorporating mapper functions as
expressions into the select block. The main change
consists of replacing the the standard list of columns
and expressions that follow the select keyword with
a list of mapper functions. A mapper function can
be identified by an expression or, alternatively, by an
inline specification of a mapper function. A particu-
lar kind of expression is a mapper function call. In
this case, the function is specified outside the select
statement using a more appropriate programming lan-
guage. We note that a similar assumption occurs w.r.t.
the computation of aggregates in SQL, in the sense
that aggregate functions like e.g.,
COUNT
or
SUM
, are
implemented elsewhere and then embedded in the se-
lect statement as parameters of the aggregation oper-
ator. An inline mapper function is specified by a map
clause followed by a list of attributes. These attributes
are the mapper function’s attributes that contribute to
the schema of the output relation. The logic of the
mapper function in this case is enclosed within a be-
gin end block.
2.2 Filters
Filters are specified through the boolean expression of
the where clause. Two kinds of filters can be speci-
fied, (i) a-priori filters, that apply to each tuple of the
input relation, which are evaluated before the mapper
and (ii) a-posteriori filters that are evaluated on the
output of the mapper, which are used to limit the map-
per results. They are identified by sub-expressions de-
fined over particular sets of columns. Sub-expressions
that are defined only over the columns of the input
relation define a-priori filters, while sub-expressions
that are defined over columns generated by the map-
per functions define a-posteriori filters.
3 OPTIMIZATION
While parsing a select block, as soon as mapper func-
tion is found, the parser knows that a mapper op-
erator is present. In this case, upon parsing the
query successfully, the parser identifies all the map-
per functions being used and the computes the out-
put schema of the mapper. The input schema of the
mapper is determined by the schema of input rela-
tions. Once the input schema is known, the input
columns specified for each mapper function can be
validated. The following step is to rewrite the fil-
ter condition into the conjunctive normal form and
validate it considering the input and output schemas.
Then, each conjunct is analyzed to decide whether
it constitutes a candidate to an a-priori or to an a-
posteriori filter. In the query presented in Figure 2, the
sub-expression
ACCOUNTS.STATUS
=
’O’
defines an a-
priori filter while the sub-expression
AMOUNT
<
50
de-
fines an a-posteriori filter.
1: select map acct(ACCT) as ACCTNO,
2: map amt(AM) as AMOUNT
3: from LOANS, ACCOUNTS
4: where ACCOUNTS.ACCTN = LOANS.ACCT
5: and ACCOUNTS.STATUS = ’O’
5: and AMOUNT < 50
Figure 2: A query that selects small payments of open ac-
counts by implementing a mapper together with a-priori and
a-posteri filters.
We note also that in some situations it is not pos-
sible to clearly separate these two kinds of filters.
For example, if the condition is dependent on both
input and output columns of the mapper like e.g.,
AMOUNT < ACCOUNTS.WDRAWLIMIT
, where
AMOUNT
is an
output attribute produced by a mapper function and
ACCOUNTS.WDRAWLIMIT
is an attribute of the input rela-
ONE-TO-MANY DATA TRANSFORMATION OPERATIONS - Optimization and Execution on an RDBMS
23

σ
AMOUNT < 50
µ
acct,amt
σ
ACCOUNTS.STATUS = ’O’
⋊⋉
ACCOUNTS.ACCTN=LOANS.ACCT
ACCOUNTS LOANS
Figure 3: Query plan representation for the query presented
in Figure 2.
tion. In these cases, the predicate can only be evalu-
ated after all the mapper functions, i.e., a-posteriori.
The specification of a-posteriori filters in the
where clause opens an interesting possibility of defin-
ing the condition using mapper functions. The sets
of values returned by mapper functions can be tested
with set operators like in or exists.
Moreover, whenever the input relation is defined
through join operations, some of the conjuncts can be
immediately pushed down into the appropriate join
operators. Generically, the query plan that results
from this process applies an a-posteriori filter to a
mapper operator. This mapper operator, in turn, is
evaluated over the input relation resulting from ap-
plying an a-priori filter to a query sub-plan that rep-
resents the input relation. This concept is illustrated
in Figure 3. Therein, the filter σ
AMOUNT < 50
is applied
to the mapper µ
acct,amt
which takes as input the tu-
ples of
ACCOUNTS
⋊⋉
ACCOUNTS.ACCTN=LOANS.ACCT
LOANS
that
are not filtered by σ
ACCOUNT.STATUS = ’O’
. The plans
so obtained are then handed to the query optimizer
where they undergo a series of rewritings that turn
them into equivalent ones that are more efficient to
evaluate. Besides the usual rewritings implemented
by RDBMSs, others, specific to mappers can be in-
troduced. Some of these rewritings are interesting
because they take direct advantage of the mapper se-
mantics. Herein, due to space limitations, we briefly
sketch the main ideas. Please refer to (Carreira et al.,
2005b; Carreira et al., 2006) for details about rewrit-
ing rules and their corresponding proofs of correct-
ness.
Projections A projection applied to a mapper is an
expression of the form π
Z
(µ
F
(s)). Those map-
per functions whose output attributes are not con-
tained in the list Z can be dropped from the map-
per since the values that they produce will not be
available for subsequent operations. Thus,
π
Z
(µ
F
(s)) = π
Z
(µ
F
′
(s)) (2)
where F
′
= { f
A
i
∈ F | A
i
contains at least one
attribute in Z}.
Selections When applying a selection to a mapper,
we can take advantage of the fact that many at-
tributes are mapped by arithmetic expressions.
Some are even simple identity functions. A selec-
tion σ
C
A
i
where C
A
i
is a condition on the attributes
produced by some mapper function f
A
i
∈ F, can
be pushed through a mapper. Hence,
σ
C
A
i
(µ
F
(s)) = µ
F
(σ
C
′
A
i
(s)) (3)
where C
′
A
i
is a rewritten condition that uses the
attributes of the input relation schema.
Joins It is often the case that mappers are applied to
joins as an expression of the form µ
F
(r ⋊⋉ s). De-
pending of the type of join being performed the
output of the relation r ⋊⋉ s can be very large. In
these cases, whenever the join is being performed
in attributes mapped by identity mapper functions,
it is possible to use the rule
µ
F
(r ⋊⋉ s) = µ
F
(r) ⋊⋉ µ
F
(s) (4)
where the mapper functions in F do not produces
duplicate values.
3.1 Plan Selection
The choice of a particular plans is governed by the
minimization of a metric of cost. The cost of a map-
per operator depends fundamentally on the costs of
evaluation each mapper function and on the cardinal-
ity of the input relation. For more details about the
cost model for the mapper operator, please refer to
(Carreira et al., 2006).
In order to estimate the cost of operators whose
input is produced by mappers, the cardinality of the
output relation produced by a mapper also needs to
be estimated. This estimation, is an interesting prob-
lem in itself, because mappers can generate variably
multiple output tuples for each input tuple. One way
to approach this issue consists of estimating the aver-
age mapper fanout factor
1
. If a mapper is being exe-
cuted for the first time, an initial estimate for its fanout
needs to be computed. This can be done by combining
the estimated the fanout factors of the mapper func-
tions involved in the mapper operator. Another inter-
esting observation is that when mapper functions re-
turn empty sets, no output tuples are produced. Thus,
the mapper in some situations may act as a filter,
which turns the selectivity of the mapper into another
1
Similarly to (Chaudhuri and Shim, 1993), we designate
the average cardinality of the output produced for each input
tuple by mappers and mapper functions as fanout.
ICEIS 2007 - International Conference on Enterprise Information Systems
24

relevant factor. Like fanout, the initial mapper selec-
tivity can also be estimated from the selectivities of
the mapper functions.
4 EXPERIMENTS
In this section we analyze the performance of the
mapper operator and consider the gains obtained with
the proposed logical optimizations. Our results in-
dicate that one-to-many data transformations can be
evaluated substantially faster than traditional database
solutions like table functions or recursive queries.
Moreover, we shall see that the optimizations defined
for mappers impart performance gains that are not
matched by traditional RDBMS solutions.
To that aim, we contrast alternative implementa-
tions of the data transformation proposed in Exam-
ple 1.1 using the mapper operator with alternative im-
plementations developed as table functions and recur-
sive queries using two leading commercial RDBMSs.
For more details on how to implement one-to-many
transformations using RDBMSs, Please refer to (Car-
reira et al., 2005a). The mapper operator was im-
plemented top of the XXL DBMS library (van den
Bercken et al., 2001) which provides database query
processing and optimization functionalities.
The database implementations were tested on two
systems henceforth designated as DBX and OEX
2
.
The parameters of both RDBMSs were carefully
aligned and the same I/O conditions where enforced
by through the usage of the same raw devices. The
hardware used was a single CPU machine (running at
3.4 GHz), with 1GB main memory RAM, and Linux
(kernel version 2.4.2) installed. Concerning work-
load, a synthetic version the input relation
LOANS
used
in Example 1.1 was employed. To equalize the record
length on XXL, DBX and OEX, a dummy column
was added to the input table.
4.1 Results
We compare throughput, i.e., the amount of work
done per second, of the distinct implementations of
one-to-many data transformations. Throughput is ex-
pressed as the ratio of source records transformed per
second and it is computed by measuring the response
time of data transformation that consists of reading
the input table, transforming it and materializing the
output table. All the timings reported were obtained
with logging disabled.
2
Due to the restrictions imposed by the license agree-
ments, the true names of the systems under test cannot be
revealed.
0
10000
20000
30000
40000
50000
60000
70000
80000
90000
Mapper/XXL TF/DBX TF/OEX SP/DBX SP/OEX RQ/DBX
Throughput [in records/sec]
Figure 4: Average throughput of the different implementa-
tions of Example 1.1 testes with input relation sizes varying
from 100K to 5M rows graphed with standard deviation. No
query results are reported for recursive queries on the OEX
system since the subset of recursive queries supported by
OEX is not powerful enough for expressing one-to-many
transformations.
The first experiment, we intended to test the raw
performance of the mapper operator for the three dis-
tinct implementations. The results depicted on Fig-
ure 4 shows that one-to-many data transformations
implemented with the mapper operator is more than 2
times better than table functions over DBX, which is
the best alternative using RDBMSs. Since the amount
I/O incurred by all the systems is similar, even con-
sidering the overhead of the RDBMSs by comparison
with XXL, we conjecture that one-to-many data trans-
formations implemented as mappers running inside
the RDBMS are very efficient. We also considered
the implementations using stored procedures. How-
ever, it turns out that the performance is quite poor
because logging cannot be disabled during their exe-
cution.
In the second set of experiments, we ana-
lyze the potential gains of logical optimizations
like those suggested in Section 3. To that aim,
we considered the evaluation of the expression
σ
ACCTNO
>p
(µ
acct,amt
(s)) together with its optimized
equivalent µ
acct,amt
(σ
ACCT
>p
(s)) obtained by pushing
down the selection. The constant p is used to in-
duce different selectivities. Moreover, we consider
that the function acct performs a direct mapping, i.e.,
is an identity function. In Figure 5, we depict the per-
formance of both the original and the optimized ex-
pressions with varying selectivities. We observe that
smaller selectivities correspond to the highest gains
of the optimized expression over the original. For
comparison, we draw the evolution of the selection
applied to one-to-many transformations implemented
using table functions on the OEX system, represented
ONE-TO-MANY DATA TRANSFORMATION OPERATIONS - Optimization and Execution on an RDBMS
25
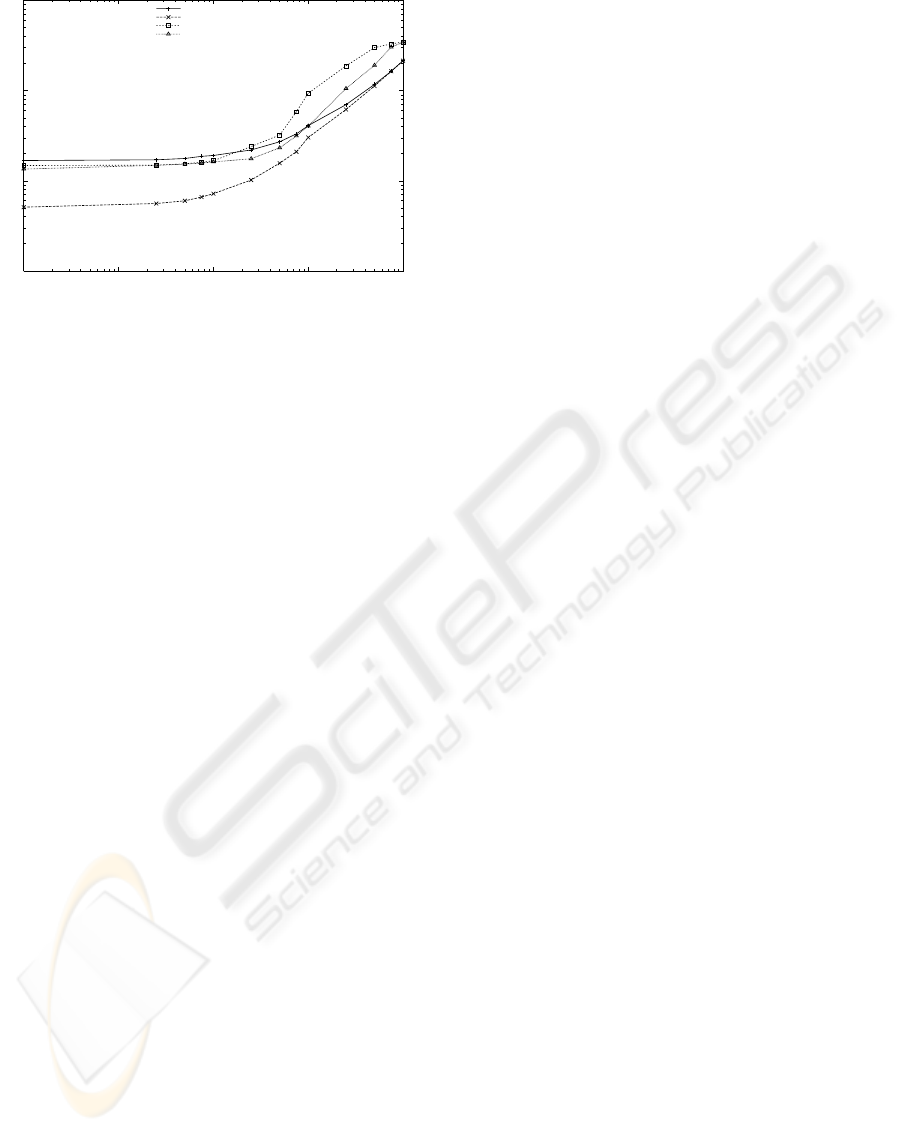
0.1
1
10
100
0.01 0.1 1 10 100
Response Time [in seconds]
Predicate selectivity factor [in %]
mapper original
mapper optimized
table function original
table function optimized
Figure 5: Evolution of response time of applying selections
to one-to-many transformations for increasing selectivity
factors plotted in logarithmic scale. The mapper original
expression refers to σ
ACCTNO
>p
(µ
acct,amt
(s)), the mapper
optimized expression refers to µ
acct,amt
(σ
ACCT
>p
(s)),
the table function original expression refers to
σ
ACCTNO
>p
(TFacct,amt(s)) and the table function op-
timized expression refers to TFacct,amt(σ
ACCT
>p
(s)). The
size of the input relation s is fixed to 1M tuples.
as σ
ACCTNO
>p
(TFacct,amt(s)). The performance of
this solution is similar the unoptimized version of
mapper and only for small selectivities. This is due
to the fact that the whole relation is read but few tu-
ples output tuples are generated.
Surprisingly, by analyzing the query plans gen-
erated by RDBMSs, we came across the fact that,
whenever table functions or recursive queries are used
to encode one-to-many data transformations, neither
DBX nor OEX are capable of pushing down a se-
lection on a directly mapped attribute. Hence, for
comparison, we also tested the corresponding opti-
mized expression TFacct, amt(σ
ACCT
>p
(s)) obtained
manually. We observed that the manually optimized
expression of the table functions bring higher gains
specially on relatively high selectivities. For high
selectivities, the response time of the original (non-
optimized) RDBMS solution increases sharply. We
conjecture that this behavior has to do with idiosyn-
crasies of OEX related with the pipelining of the tu-
ples resulting from the table function into the selec-
tion operator.
5 CONCLUSION
In this paper we focused on the feasibility of incor-
porating a specialized operator for handling one-to-
many data transformations on an RDBMSs. This ex-
tension is attractive, not only because one-to-many
data transformations cannot be expressed using rela-
tional algebra but also because data usually resides
in an RDBMS. We outlined the concrete syntax for
this operator and then examined how a query op-
timizer can be extended to consider more advanta-
geous execution plans in the presence of mappers.
To test our ideas we analyzed experimentally differ-
ent implementations of one-to-many data transforma-
tions using mappers and contrasted them with tradi-
tional implementations using table functions and re-
cursive queries using two industry-leading RDBMSs.
To best of our knowledge, this is the first experimen-
tal assessment of one-to-many data transformations
on RDBMSs.
The experiments showed that a native implemen-
tation of the mapper operator outperformed the best
RDBMS solution by almost 3 times. We have also
observed that RDBMSs do not in general perform
even very simple but highly valuable optimizations
when table functions and recursive queries are used.
Thus, we posit that one-to-many data transformations
expressed by combining standard relational operators
and mappers constitute a valid alternative.
The simple iterator-based semantics of the map-
per operator enables efficient executions of one-to-
many data transformations and favors an easy inte-
gration into the query processor of a database sys-
tem. Towards physical optimization, we are devel-
oping different algorithms for the mapper operator
to take advantage of duplicate values by employing
caching techniques and hybrid-hashing proposed by
(Hellerstein, 1998). Additionally, we consider incor-
porating the mapper operator in Apache Derby open
source RDBMS (Apache, 2005).
One limitation of our work is that, despite the ef-
fort to configure the different systems so that they run
in similar conditions, the alignment of these configu-
rations lacks quantification. To address this shortcom-
ing we consider running TPC-H (TPC, 1999) loads on
the different systems in order to obtain a metric for
comparing their respective configurations.
REFERENCES
Aho, A. V. and Ullman, J. D. (1979). Universality of data
retrieval languages. In Proc. of the 6th ACM SIGACT-
SIGPLAN Symposium on Principles of Programming
Lang., pages 110–119. ACM Press.
Amer-Yahia, S. and Cluet, S. (2004). A declarative ap-
proach to optimize bulk loading into databases. ACM
Transactions of Database Systems, 29(2):233–281.
Apache (2005). Derby homepage.
http://db.apache.org/derby.
Carreira, P., Galhardas, H., Lopes, A., and Pereira, J.
(2005a). Extending the relational algebra with the
ICEIS 2007 - International Conference on Enterprise Information Systems
26

Mapper operator. DI/FCUL TR 05–2, Depart-
ment of Informatics, University of Lisbon. URL
http://www.di.fc.ul.pt/tech-reports
.
Carreira, P., Galhardas, H., Lopes, A., and Pereira, J.
(2006). One-to-many transformation through data
mappers. Data and Knowledge Engineering Journal
(DKE), Elsevier Science.
Carreira, P., Galhardas, H., Pereira, J., and Lopes, A.
(2005b). Data mapper: An operator for expres-
siong one-to-many data transformations. In 7th Int’l
Conf. on Data Warehousing and Knowledge Discov-
ery, DaWaK ’05, volume 3589 of LNCS. Springer-
Verlag.
Chaudhuri, S. (1998). An overview of query optimization
in relational systems. In PODS ’98: Proc. of the ACM
Symp. on Principles of Database Systems, pages 34–
43. ACM Press.
Chaudhuri, S. and Shim, K. (1993). Query optimization in
the presence of foreign functions. In Proc. of the Int’l
Conf. on Very Large Data Bases (VLDB’93), pages
529–542.
Cui, Y. and Widom, J. (2001). Lineage tracing for general
data warehouse transformations. In Proc. of the Int’l
Conf. on Very Large Data Bases (VLDB’01).
Eisenberg, A., Melton, J., Michels, K. K. J.-E., and Zemke,
F. (2004). SQL:2003 has been published. ACM SIG-
MOD Record, 33(1):119–126.
Galhardas, H., Florescu, D., Shasha, D., and Simon, E.
(2000). Ajax: An extensible data cleaning tool. ACM
SIGMOD Int’l Conf. on Management of Data, 2(29).
Garcia-Molina, H., Ullman, J. D., and Widom, J. (2002).
Database Systems – The Complete Book. Prentice-
Hall.
Haas, L. M., Miller, R. J., Niswonger, B., Roth, M. T.,
Schwarz, P. M., and Wimmers, E. L. (1999). Trans-
forming heterogeneous data with database middle-
ware: Beyond integration. IEEE Data Engineering
Bulletin, 22(1):31–36.
Hellerstein, J. M. (1998). Optimization techniques for
queries with expensive methods. ACM Transactions
on Database Systems, 22(2):113–157.
Lomet, D. and Rundensteiner, E. A., editors (1999). Spe-
cial Issue on Data Transformations, volume 22. IEEE
Data Engineering Bulletin.
Melton, J. and Simon, A. R. (2002). SQL:1999 Understand-
ing Relational Language Components. Morgan Kauf-
mann Publishers, Inc.
Rahm, E. and Do, H.-H. (2000). Data Cleaning: Problems
and current approaches. IEEE Bulletin of the Techni-
cal Comittee on Data Engineering, 24(4).
Raman, V. and Hellerstein, J. M. (2001). Potter’s Wheel:
An Interactive Data Cleaning System. In Proc. of the
Int’l Conf. on Very Large Data Bases (VLDB’01).
TPC (1999). Benchmark H standard specification.
http://www.tpc.org.
van den Bercken, J., Dittrich, J. P., Kr
¨
aamer, J., Sch
¨
aafer,
T., Schneider, M., and Seeger, B. (2001). XXL A
library approach to supporting efficient implementa-
tions of advanced database queries. In Proc. of the
Int’l Conf. on Very Large Data Bases (VLDB’01).
ONE-TO-MANY DATA TRANSFORMATION OPERATIONS - Optimization and Execution on an RDBMS
27
