DEVELOPMENT OF AN ACCOUNTING SYSTEM
Applying the Incrementally Modular Abstraction Hierarchy to a Complex System
Kenji Ohmori
Computer and Information Sciences, Hosei Univeristy, 3-7-2 Kajino-cho, Koganei-shi, Tokyo, 184-8584, Japan
Tosiyasu L. Kunii
IT Institute, Kanazawa Institute of Technology, 1-15-13 Jingumae, Shibuya-ku, Tokyo, 150-0001, Japan
Keywords: An enterprise system, an accounting system, software engineering, software development, homotopy, fiber
bundles, invariant, abstraction hierarchy.
Abstract: The new methodology for software development is introduced and applied to an accounting system. The
new method is called the incrementally modular abstraction hierarchy (IMAH). IMAH has an abstraction
hierarchy from abstract to concrete levels. Invariants defined on an abstract level are kept on a concrete
level, which allows adding modules incrementally on each hierarchical level and avoiding combinatorial
explosion of the serious problem in software engineering, while climbing down abstraction hierarchy in
designing and modeling a complex system. This paper shows how IMAH is applied in developing an
accounting system, which is fundamental in enterprise systems and a suitable example of complex software
systems. At first, very simple example recording only journal vouches to a database system is used to
describe methodologies of IMAH. Then, it is described how this simple system is incrementally developed
to a conventional complex accounting system.
1 INTRODUCTION
Many software development methodologies have
been proposed. (Dahl, Dijkstra and Hoare 1972).
(Naur et al 1976). (Jackson 1975). (Halstead 1977).
(Myers 1978). (Yordon and Constantine 1979).
(Boehm 1981). (Agresti 1986). (Humphrey 1989).
(Booch 1991). (Rumbaugh 1991). (Jacobson 1992).
(Soley, Frankel and Parodi 2004). However,
conventional software development methodologies
have not solved yet a so-called combinatorial
explosion problem, which is a fundamental problem
since the study of software engineering started in
1970s. Combinatorial explosion is caused when a
new component is added to a developing system
since component addition leads to combinatorially
complicated modification in most parts of the
system.
The rational process model (RUP) is proposed to
avoid this problem recently by repeating
development process. (Jacobson, Booch and
Rumbaugh, 1999). (Booch, Rumbaugh and Jacobson
1999). (Rumbaugh, Jacobson and Booch 1999).
RUP divides a system into multiple subsystems. The
most difficult subsystem among them is firstly
developed in accordance with engineering
disciplines starting from a business model and
requirements and ending with test and development.
When this subsystem is successfully completed,
RUP moves to the following most difficult
subsystem for development. As a result, RUP makes
development feasibility clear at an early stage so that
a project manager can control software development
by giving correct judgments at each stage. RUP
succeeds in raising the success rate of projects. RUP
tries to decrease as much as possible opportunities of
combinatorial explosion by iterative and incremental
development. However, as it does not solve
combinatorial explosion theoretically, RUP is still
annoyed by the unsolved problem.
The incrementally modular abstraction hierarchy
(IMAH), which is based on homotopy and topology,
is introduced in this paper. (Sieradski 1992).
(Spanier 1996). (Hatcher 2002). (Kunii 2005).
(Kunii 2006). (Ohmori 2006). IMAH avoids
combinatorial explosion by adding invariants
linearly while climbing down abstraction hierarchy,
keeping invariants defined on higher abstract levels
and adding linearly new invariants on the current
437
Ohmori K. and L. Kunii T. (2007).
DEVELOPMENT OF AN ACCOUNTING SYSTEM - Applying the Incrementally Modular Abstraction Hierarchy to a Complex System.
In Proceedings of the Ninth International Conference on Enterprise Information Systems - DISI, pages 437-444
DOI: 10.5220/0002372504370444
Copyright
c
 SciTePress

abstract level. RUP enforces developers to design
and model a system using unified modeling
language (UML) diagrams. With the progress of
development, many components are added to the
diagram step by step. However, inevitability of these
components, for example why these components are
necessary or satisfy requirements, is not clear. When
designing a class diagram, it is hard to explain
theoretically why we need to put a new class in the
diagram, or why this class has to have an association
link with another class. This theoretical ambiguity
leads to repeated modification of classes and class
links, sometimes endlessly, as the development
advances. This is a basic reason why RUP cannot
avoid the combinatorial explosion problem
theoretically.
In contrast, IMAH uses UML diagrams on a
lower level in abstraction hierarchy. As IMAH
provides theoretically fundamental properties for a
class on higher abstract levels, the class has been
already defined with necessary properties when it
appears in a class diagram on a lower abstract level,
which does not bring any modification of classes in
the lower level.
In this paper, the accounting system
development is described as an example for showing
how a complicated enterprise information system is
developed by IMAH. The accounting system is a
fundamental system for enterprise resource planning
(ERP) and gains importance with introduction of the
Sarbanes–Oxley Act of 2002 (SOX). (Ohmori 2005).
The SOX requires accountabilities of initiating,
authorizing, processing, and reporting of financial
data. A Web-base system, which allows financial
data to be directly entered on site, is the most
suitable system for SOX environments. In this paper,
IMAH disciplines are firstly explained using a
simple accounting system and designing of a full-
scale Web-base accounting system is then described.
2 INCREMENTALLY MODULAR
ABSTRACTION HIERARCHY
IMAH is based on the abstraction hierarchy in
algebraic topology and consists of seven abstract
levels.
1) The homotopy level is the most abstract level in
the hierarchy. On the homotopy level, the
developing system is described using a fiber
bundle. The fiber bundle defines the most
fundamental spaces constituting the developing
system. The relation of these spaces is also
provided on this level. As homotopy is
continuous changes of continuous functions,
dynamic changes can be represented using
homotopy. Conceptual progress, which is
thought as dynamic changes from the original
concept to the current one, is described using
homotopy extension properties (HEP) or
homotopy lifting properties (HLP). A simple
accounting system is described using a fiber
bundle and a Web-base accounting system,
which is conceptual progress originated from
the simple accounting system, is described by
HEP or HLP.
2) The set theoretical level is the following most
abstract level. Elements consisting of the spaces
defined on the above level are defined and
incrementally added on this level. Logical
operations are also available from this level.
3) The topology space level is the third highest
abstract level. Continuity and closeness are
defined on this level. Topological equivalence is
one of the most important invariants, which are
defined on this level. As the accounting system
has discrete spaces, strong or weak topology is
used to describe these spaces.
4) The adjunction space level is the middle
abstract level. Dynamic changes are handled
here. It occurs when two spaces are attached
together or detached separately. The accounting
system is the description of transactions, where
entities such as products and cash are
exchanged between two agents. When a
transaction occurs, some entities are detached
from one agent and attached to another agent.
These dynamic changes are expressed using an
attaching function.
5) The cellular structure level is the third lowest
abstract level. The physical structure of the
system is defined here. Up to now, the
designing system is conceptual and difficult to
capture its physical structure. On this level, an
element constituting a space is represented by a
cellular structure, which is imaginary similar to
embryos and constructed by n-dimensional
cells.
6) The presentation level is the following lowest
abstract level. On this level, UML diagrams are
used to represent the developing system. From
this level, an accounting system is designed or
modeled in the same way as RUP. However, as
properties of classes have already been defined
on the precedent abstract levels, UML diagrams
are created almost automatically. This is the big
difference with the traditional methodologies.
7) The view level is the lowest abstract level and
the most concrete level. On this level, the
system is represented by program codes. If
program codes are installed in the system, the
ICEIS 2007 - International Conference on Enterprise Information Systems
438

behavior of the developing system can be
observed.
3 DESIGNING AND MODELING
OF AN SIMPLE ACCOUNTING
SYSTEM
3.1 The Homotopy Level
A simple accounting system is the description of
transactions in a company. A company buys parts
and sells products. The difference of amount
between buying and selling is profit or loss. When a
transaction occurs, a journal voucher is issued. A
journal voucher consists of a journal voucher
number, header and details. IMAH maps these
materials into a fiber bundle. A fiber bundle is
defined mathematically as follows.
Definition: A fiber bundle is a quadruple ξ = (E,
B, F, p) consisting of a total space E, a base space
B, a fiber F, and a bundle projection that is a
continuous surjection called F-bundle p: E → B
such that there exists an open covering Υ = {U} of B
and, for each U ∈ Υ, a homeomorphism called a
coordinate chart ϕ
U
: U × F → p
-1
(U) exists such
that the composite
U × F  p
-1
(U)  U
is the projection to the first factor U. Thus the
bundle projection p: E → B and the projection p
B
: B
× F → B are locally equivalent. The fiber over b ∈
B is defined to be equal to p
-1
(b), and we note that F
is homeomorphic to p
-1
(b) for every b ∈ B, namely
∀b ∈ B, F > p
-1
(b).
The total space for the simple accounting system
is of course the transaction space. A fiber bundle
divides a total space into a base space and a fiber. As
the base space is projection of the total space, the
journal voucher frame space J, which is a frame to
contain the description of a transaction, is
determined as the base space. The inverse map of
projection to an element of the base space represents
a fiber. A journal voucher number space V, a header
space H and a detail space D, which represent the
description of a transaction, compose a fiber as
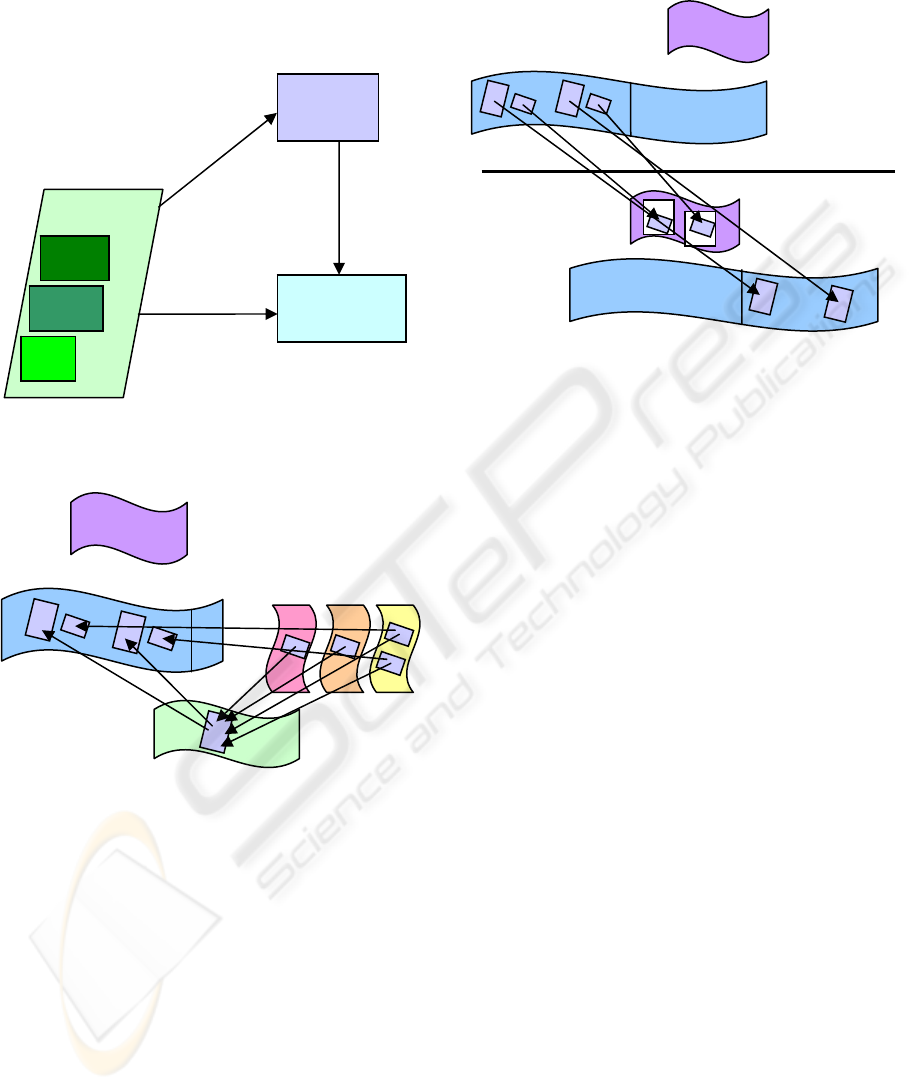
shown in Figure 1.
When a transaction occurs, the elements are
obtained from these spaces and combined each
other, where a space and an element are similar
concepts to a class and an instance of an object
oriented language. Therefore, a journal voucher
frame is obtained from the space J. A journal
voucher number, a header and a set of details are
obtained from the spaces V, H and D. The journal
voucher number, the header and the set of details are
put in the journal voucher frame.
Figure 1. The fiber bundle for the simple accounting
system.
In summary, the journal voucher frame space J,
the journal voucher number space V, the header
space H and the detail space D have been defined on
this level.
3.2 The Set Theoretical Level
Elements of a space are defined on this level. The
journal voucher frame space J consists of a set of
journal voucher frames: J = {j
1
, j
2
,…., j
n
}, where j
i
is
a journal voucher frame with three variables such
that j
i
= (v
i
, h
i
, DS
i
) ∈ J, where v
i
, h
i
and DS
i
are a
journal voucher number, a header and details. The
journal voucher number space V consists of journal
voucher numbers: V = {v
1
, v
2
,….,v
s
}, where v
i
is a
journal voucher number with one variable of s
i
∈ ⊆.
The header space consists of headers: H = {h
1
,
h
2
,….,h
s
}, where h
i
is a header with three variables
such that h
i
= (t
i
, a
i
, r
i
) ∈ H, where t
i
, a
i
and r
i
are
application date, applicant name and remarks. The
detail space consists of a set of details: D = {d
1
,
d
2
,…..,d
j
}, where d
i
is a detail with two variables
such that d
i
= (di
i
, da
i
), where di
i
, da
i
are an
accounting item and amount. If amount is positive,
the detail is debtor, otherwise it is creditor.
In summary, the elements of each space: J = {j
1
,
j
2
,…., j
n
}; V = {v
1
, v
2
,….,v
s
}; H = {h
1
, h
2
,….,h
s
} and
D = {d
1
, d
2
,…..,d
j
} are defined on this level. The
variables of each element are also defined on this
level. The elements and variables are incrementally
added on the basis of the invariants defined on the
homotopy level.
ϕ
p
A journal voucher
frame space
A detail
space
A header
space
A journal
voucher
space
DEVELOPMENT OF AN ACCOUNTING SYSTEM - Applying the Incrementally Modular Abstraction Hierarchy to a
Complex System
439

3.3 The Topological Space Level
The strongest topology is introduced for the simple
accounting system. The strongest topology for the
journal voucher space J is introduced as follows. (J,
T) = {φ, j
1
, j
2
, j
3
,…, j
n
, (j
1
, j
2
), (j
1
, j
3
),…, (j
n-1
,
j
n
),……., (j
1
, j
2
, j
3
,…, j
n
) }. Other spaces also have
the strongest topology in the same way.
Here is an example how the topological space is
used. When the general ledger is required, it is
necessary to collect journal vouchers with a given
accounting item. This requirement is achieved by
gathering fibers as shown in Figure 2. For example,
if all transactions traded with account receivable are
projected to a subset Js ⊂ (J, T), then the set of
fibers of Js gives the voucher numbers, headers and
details of all the journal vouches traded with account
receivable.
Figure 2. Fibers for account receivable.
In summary, the topological space level defines
topological spaces, for example (J, T) = {φ, j
1
, j
2
,
j
3
,…, j
n
, (j
1
, j
2
), (j
1
, j
3
),…, (j
n-1
, j
n
),……., (j
1
, j
2
, j
3
,…,
j
n
) }, on the basis of invariants defined by the
previous abstract levels.
3.4 The Adjunction Space Level
When a transaction occurs, the space J is attached to
the spaces V, H and D such that the journal voucher
number, header and details are put in the journal
voucher frame. This behavior is clearly represented
on the adjunction space level, where related spaces
are adjoined by an attaching function.
Dynamic relations between the journal voucher
frame space J and the detail space D are considered
here as an example. When a transaction occurs, the
spaces J and D are adjoined by identifying
transaction details. That is, a journal voucher frame
j
i
, is attached to a journal voucher numbar v
i
(s
i
), a
header h
i
(t
i
, a
i
, r
i
) and details d
i1
(di
i1
, ai
i1
) …..
d
ik
(di
ik
, ai
ik
). This attachment is carried out by
adjoining two spaces. Using an attaching function f,
the adjunction space D
f
D
f
= D +
f
J = D + J / ∼ = D + J / (j
i
∼ f(y) | j
i
∈ J,
∀y ∈ D
0
)
is obtained by identifying each of transaction details
y ∈ D
0
| D
0
⊆ D with its image f(y), which is a
journal voucher frame ∈ J, so that j
i
∼ f (y) | ∀y ∈
D
0
. The adjunction space D
f
shows the shape of the
space D where D
0
⊆ D affected by this transaction is
identical to the corresponding part of the space J.
The attaching map f and the identification map g
are:
f: D
0
→ J | D
0
⊆ D,
and
g: D + J → D
f
= D +
f
J = D + J / ∼
= D + J / (j
i
∼ f(y) | j
i
∈ J, y ∈ D
0
).
The attaching map shows how D
0
⊆ D is mapped
into J. The identification map shows how relations
of two spaces D and J change after mapping f.
These relations are shown in Figure 3.
Figure 3. The attaching function.
The adjunction space level preserves the
invariants defined at the homotopy level. The
invariant showing that the journal voucher consists
of three properties of a journal voucher number, a
header and details is preserved by the attaching map
f. These spaces are attached by a disjoint union.
As an attaching map is continuous, the reverse
function is defined. It means that the system can
return at the point before applying the attaching map.
Therefore, cancellation of any transaction can be
accepted at any time, which gives flexibility to
system development.
In summary, attaching maps from V, H and D to
J are defined on the basis of invariants defined by
the previous higher abstract levels.
3.5 The Cellular Structure Level
On this level, the physical structure is constructed
using cells. At first, an element in each space is
Transactions
The journal
voucher A
The journal
voucher B
J
s
Journal voucher
frames
f (y)
j
Acc Item
Amount
Details
The attaching map
f
An accounting system
Acc Item
Amount
A voucher
frame
Detail
The adjunction space J
f
The identification
map g
Detail
Transaction
J + D
A voucher
frame
Journal voucher
frames
Details
ICEIS 2007 - International Conference on Enterprise Information Systems
440

transformed to an n-dimensional ball. A journal
voucher number v
i
has one variable of an integer
number. It is represented by Β
si
1
. As the journal
voucher number space V is disjoint unions of journal
voucher numbers, it is represented by +
i
Β
si
1
. A
header h
i
and a detail d
i
have three and two variables.
These spaces H and D are represented by +
i
Β
hi
3
and
+
i
Β
di
2
. A journal voucher frame j
i
is a container of
these elements without variables, its space J
becomes +
i
Β
i
0
.
A n-dimensional closed ball is represented by
disjoint unions of a (n-1)-dimensional open ball and
a (n-1)-dimensional surface and (n-1)-dimensional
closed balls such that
Β
n
= intΒ
n
+ (S
n-1
\ +
j
Β
j
n-1
) +
j
Β
j
n-1
.
A smaller dimensional closed ball Β
j
k
than the
original ball is obtained by repeating this process.
This ball is denoted by the following expression.
∂
n-k
Β
n
= Β
k
.
A journal voucher frame j
i
is attached to a
journal voucher number v
i
, a header h
i
and details
DS
i
. These attaching is described by the following
equations.
f
1
: ∂
1
Β
sj
1
→ Β
j
0
, or Β
j
0
+
f1
Β
sj
1
/~.
f
2
: ∂
3
Β
hj
3
→ Β
j
0
, or Β
j
0
+
f2
Β
hj
3
/~.
f
3
: +
j
∂
2
Β
djj
2
→ Β
j
0
, or Β
j
0
+
f3
(+
j
Β
djj
2
)/~.
Then, n-dimensional balls are transformed into
cellular structures using a filtration.
Definition: A filtration space is a sequence of cells
to represent a topological space. It is defined as
follows. For any topological space X, we can get a
finite or infinite sequence of skeletons X
p
, where p is
an integer, such that
X = ∩
p ∈ Z
X
p
X
0
⊆ X
1
⊆ …… ⊆ X
p
…… ⊆ X.
A skeleton X
p
consists of cells, whose
dimensions do not exceed n. A cell is a topological
space, equivalent topologically to an n-dimensional
open ball IntΒ
n
, where n is an arbitrary integer. A
sequence of skeletons is called filtration. If it is
finite, it becomes a CW-space.
Let’s consider details DS
i
. DS
i
is represented by
+
j
Β
dji
2
using open balls. A detail has an accounting
item and amount as its variables. It also needs an
index to be uniquely identified. These entities are
used as a skeleton X
detail
0
of DS
i
.
X
detail
0
={e
did
0
1
, .., e
did
0
k
, e
item
0
1
, .., e
item
0
k
, e
amount
0
1
, .., e
amout
0
k
}.
For the skeleton X
detail
1
, every two entities among
index, accounting item and amount are attached
together via 1-dimensional cells as follows.
X
detail
1
={X
detail
0
, e
diditem
1
1
, .., e
diditem
1
k
, e
itemamount
0
1
,
.., e
itemamount
0
k
, e
amoundidt
0
1
, .., e
amoutdid
0
k
| f
1
: ∂e
diditem
1
i
→ e
did
0
i
, f
2
: ∂e
diditem
1
i
→ e
item
0
i
, f
3
: ∂e
itemamount
1
i
→
e
item
0
i
, f
4
: ∂e
itemamount
1
i
→ e
amount
0
i
, f
5
: ∂e
amountdid
1
i
→
e
amount
0
i
, f
6
: ∂e
amountdid
1
i
→ e
did
0
i
,}.
The keleton X
detail
2
is also obtained as follows.
X
detail
=
X
detail
2
={X
detail
1
, e
detail
2
1
, .., e
detail
2
k
| f
1
:
∂e
detail
2
i
→ e
diditem
1
i
, f
2
: ∂e
detail
2
i
→ e
itemamount
0
i
, f
3
:
∂e
detail
2
i
→ e
amoutdid
0
i
}.
In the same way, a journal voucher number v
i
and a header h
i
are obtained. These are attached to a
journal voucher frame j
i
as shown in figure 4.
Figure 4. The cellular structures for the simple
accounting system.
In summary, the cellular structures of elements
for the spaces J, V, H and D are defined while
preserving invariants defined on the previous higher
levels.
3.5 The Presentation Level
The journal voucher frame j
i
∈ J, the journal
voucher number v
i
∈ J, the header h
i
∈ J, the details
DS
i
⊂ D constituting a transaction have been
represented as cellular structures X
frame
, X
number
,
X
header
and X
detail
on the cellular structure level.
These cellular structures are transformed into UML
diagrams on the presentation level as shown in
Figure 5. Each cellular structure is represented as a
class such that X
frame
is represented as class
VoucherFame, with stereo type entity, which
becomes an entity been of Enterprise Java Beans
(EJB) on the next view level. The elements of a 0-
dimentional skeleton are transformed into instant
variables. The attaching function between two cells
is transformed into an association links. Multiplicity
of an association link reflects the number of cells
connected by the attaching function. In a cellular
structure, an index is used in a 0-dimentional
index
index serial #
index
item
amount
index
item
amount
index
application
date
applicant
name
remarks
X
f
rame
X
numbe
r
X
heade
r
X
detai
l
attaching
DEVELOPMENT OF AN ACCOUNTING SYSTEM - Applying the Incrementally Modular Abstraction Hierarchy to a
Complex System
441

skeleton. It does not appear in its class. However, it
becomes the primary key when a class is
transformed into the database table using object-
relational mapping on the next view level.
In summary, a space defined on the homotopy
level is transformed into a class with stereotype
entity on this level. An element defined on the set
theoretical level is transformed into a cell on the
cellular structure level and into an instance on this
level. A variable defined on the set theoretical level
is transformed into a 0-dimentional cell on the
cellular structure level and into an instance variable
on this level. An attaching function defined on the
adjunction space level is transformed into an
association link connecting two classes.
3.6 The View Level
The simple accounting system includes only classes
with stereo type entity. These classes are
automatically transformed into entity beans and
database tables by AndroMDA. AndroMDA is a
generator framework that adheres to the model
driven architecture (MDA) paradigm. UML
diagrams are transformed into deployable
components for J2EE, Spring or .NET platform.
Any business logic is not included in the simple
accounting system. Only, creating, reading, updating
and deleting are necessary for the database. Java
server pages (JSP) realizing these functions are also
automatically generated by AndroMDA.
In summary, as everything which is necessary as
an application program in EJB environment is
automatically generated by AndroMDA, invarinats
defined on the previous levels are preserved here
and components required for deploying the system is
incrementally added on this level.
4 DESIGNING AND MODELING
OF A FULL-SCALE WEB-BASE
ACCOUNTING SYSTEM
4.1 The Homotopy Level
A full-scale accounting system is provided by
adding functions to the simple accounting system. A
basic accounting system is obtained by adding
general ledgers to the simple accounting system. An
enterprise accounting system is equipped with
financial statements to the basic accounting system.
A full-scale Web-base accounting system with
internal auditing functions is obtained by adding a
business process model to the enterprise accounting
system in Web-base environment. The conceptual
progress from the simple accounting system to the
full-scale Web-base accounting system is explained
by HLP. HLP is defined mathematically as follows.
The function p: E → B has the homotopy lifting
property (HLP) for a space X if, for each continuous
function k: X → E, each homotopy H: X  I → B of
p
⎣ k (H⎣i
0
= p⎣k) has a lifting to a homotopy K: X  I
→ E of k (K⎣i
0
= k) and K is constant on {x}  I
whenever H is constant on {x}  I.
If space X represents conceptual progress and E
and B are a total space representing transactions and
a base space representing journal vouchers as shown
in Figure 6, the conceptual progress to the full-scale
accounting system is considered as homotopical
changes originated from the simple accounting
system.
Therefore, the conceptual progress preserves
invariants of the simple accounting system. For the
full-scale Web-base accounting system, the journal
voucher frame space J, the journal voucher number
space V, the header space H and the detail space D
are preserved. The invariants for conceptual progress
part are incrementally added to the original part.
The basic accounting system, which enhances
the simple accounting system by adding the function
of the general ledger, is considered as the first
conceptual progress. The general ledger is a
permanent summary of all journals. The general
ledger is sometimes divided into main accounting
items, such as cash, account receivable and account
payable ledgers. The general ledger is created from a
set of journal vouchers. It is possible to create it
whenever a journal voucher is processed or only
Figure 5. The class diagram for the simple accounting
system.
<<entity>>
Detail
accountingItem: String
amount: Money
<<entity>
Header
applicationDate: Date
applicantName : String
remarks : String
<<entity>>
SerialNumber
<<unique>>number: Integer
<<entity>>
VoucherFrame
1
1..n
1
ICEIS 2007 - International Conference on Enterprise Information Systems
442

when the reference of the general ledger is requested.
The system is designed by the latter since it is
expected the former takes time when the system
becomes a full-scale system.
Figure 6. The homotopy lifting properties.
To fulfill the above requirements, the basic
accounting system is designed as follows. It adds the
general ledger space and the processing list space to
the spaces defined for the simple accounting system
as shown in Figure 7. The general ledgers are
generated on the general ledger space. The
processing list space is divided into two subspaces:
waiting and processed. Journal vouchers which have
not been recorded yet in the general ledger are kept
in the waiting space. When a journal voucher is
recorded, it is moved to the processed space. The
basic accounting system has two main procedures:
1) processing of a journal voucher, which carries out
the same process as in the accounting system as well
as saves it in the waiting space; 2) updating of the
general ledger, which moves journal vouches from
the waiting space to the processed space and add
amount recorded in the journal voucher to the
current total amount of the corresponding
accounting item as shown in Figure 8.
Figure 8. General ledger updating process.
4.2 The Presentation Level
After designing the basic accounting system on the
homotopy level, it goes to designing on the lower
abstract levels in the same way as the simple
accounting system. The results on the presentation
level are shown in Figure 9. In the simple
accounting system, all classes have stereo type entity.
However, in the basic accounting system, processing
of the general ledger requires business logic. A class
with business logic has stereo type service. This
class becomes a session bean of EJB. In the Figure
10, GeneralLegerHandler is equipped for this
purpose. The method getGeneralLedger() of class
GeneralLegerHandler updates the general ledger.
The contents of this method, which is business logic
of the basic accounting system, is not automatically
generated by AndroMDA, a programmer has to
supply its code. This program development is also
carried out by abstraction hierarchy. A finite
machine, where equivalent finite machines are
homotopically equivalent, is defined on the
homotopy level. As the explanation of this
mechanism needs more space, it will be described in
another paper.
After completing the development of the basic
accounting system, the enterprise accounting system
is developed in the same way starting from the
homotopy level and ending with the view level. The
full-scale accounting system is finally completed by
repeating this process. This process is similar to
RUP. However, RUP repeats it between the
presentation and view levels, while IMAH repeats it
between the homotopy and view levels with
theoretical basis.
Figure 7. The spaces for the basic accounting system.
A general ledger space
A processing list space
A general ledger space
A processing list space
waiting
waiting
processed
processed
item1
item2
Get a general ledger
A voucher frame space
A general ledger space
A processing list space
waiting
processed
A detail
space
A header
space
A serial #
space
Transaction
Voucher Frame
B: A Base Space
E: A total Space
A journal voucher
+ BPM
+ GL
+ BSPL
H
X x I
DEVELOPMENT OF AN ACCOUNTING SYSTEM - Applying the Incrementally Modular Abstraction Hierarchy to a
Complex System
443

Figure 9. The class diagram for the basic accounting
system.
4 CONCLUSIONS
IMAH is applied to the development of accounting
systems ranging from the simple accounting system
to the full-scale Web-base accounting system.
IMAH keeps invariants defined on higher abstract
levels while climbing down the abstraction hierarchy.
Using the simple accounting system, it is described
how invariants are incrementally added to the
developing system. The incremental invariant
addition contributes to avoiding the combinatorial
explosion problem.
The simple accounting system is enhanced to the
basic accounting system and the full-scale Web-base
accounting system. The conceptual progress also
keeps invariants defined in the original system.
IMAH is considered as the conceptual progress of
RUP since both methodologies are performed by
iterative process. However, IMAH is different from
RUP since IMAH has theoretical background.
Homotopy, fiber bundles, homotopy lifting
properties, homotopy extension properties, topology,
attaching functions and cellular structures give
enough theoretical background to software
engineering.
REFERENCES
Agresti, W. W., 1986. New Paradigms for Software
Development. IEEE Tutorial, IEEE Computer Society.
Boehm, B., 1981. Software Engineering Economics.
Prentice-Hall. Englewood
Booch, G., 1991. Object Oriented Design with
Applications. The Benjamin/Cummings Publishing
Company.
Booch, G., Rumbaugh, J., Jacobson, I., 1999. The Unified
Modeling Language User Guide. Addison-Wesley.
Dahl, O. J., Dijkstra, E. W. Hoare, C. A. A., 1972.
Structured Progamming. Academic Press, London.
Dodson, C. T. J., Parker, P. E., 1997. A user’s guide to
algebraic topology. Kluwer Academic Publication.
Halstead, M. H. 1977. Elements of Software Science.
North-Holland, Amsterdam.
Hatcher, A., 2002. Algebraic topology. Cambridge
University Press.
Humphrey, W. S., 1989. Managing the Software Process.
Addison-Weskey, Reading Mass.
Jackson, M. A., 1975. Principles of Program Design.
Academic Press, New York.
Jacobson, I. et. Al. 1992. Object-Oriented Softwae
Engineering – A Use Case Driven Approach, ACM
Press.
Jacobson, I., Booch, G., Rumbaugh, J., 1999. The Unified
Software Development Process. Addison-Wesley.
Kunii, L. T., 2005. Cyberworlds -Theory, Design and
Potetial-, The Institute of Electronics, Information and
Communication Engineers, E88-D(5), 790-800
Kunii, T. L., and Ohmori, K., 2006. Cyberworlds:
Architecture and Modeling by an Incrementally
Modular Abstraction Hierarchy, The Visual Computer,
22(12), 949-964.
Myers, G. J., 1978. Composite / Structure Design, Van
Nostrand Reinhold, New York.
Naur et al, 1976. Software Engineering: Concepts and
Techniques. Petrocelli/Charter, New York.
Ohmori, K., 2005 An Internet Accounting System: A
Large Scale Software Development Using Model
Driven Architecture, Seventh International Conference
on Enterprise Information Systems, 407-410
Omori K., and Kunii T. L., 2006. An Incrementally
Modular Abstraction Hierarchy for Linear Software
Development Methodology, International Conference
on Cyberworlds, 216-223
Rumbaugh, J. et. Al. 1991. Object-Oriented Modeling and
Design. Prentice-Hall. N. J.
Rumbaugh, J., Jacobson, I., Booch, G., 1999. The Unified
Modeling Language Reference Manual. Addison-
Wesley.
Sieradski, A. J., 1992. An introduction to topology and
homotopy. PWS-Kent Publishing Company. Boston.
Soley, R., Frankel, D. S., Parodi, J., 2004. The MDA
Journal: Model Driven Architecture Straight From The
Masters, Meghan Kiffer Pr.
Spanier, E. H., 1996. Algebraic topology, Springer-
Verlag.
Yordon, E., Constantine, L. L. 1979. Structured Design:
Fundamentals of Decipline of Computer and System
Design. Prentice-Hall, Englewood Cliffs, N. J.
http://www.andromda.org/.
<<entity>>
ProcessingList
<<service>
GeneralLedgerHandler
getGeneralLedger():void
<<entity>>
Voucher
<<entity>
Header
applicationDate: Date
applicantName : String
remarks : String
<<entity>>
Detail
accountingItem: String
amount: Money
1
1.
<<entity>>
SerialNumber
<<unique>>number: Integer
1
<<entity>
GeneralLedger
accountingItem: String
totalAmount : Money
parent
processed
waiting
0..n
0..n
ICEIS 2007 - International Conference on Enterprise Information Systems
444