USING AN INDEX OF PRECOMPUTED JOINS IN ORDER TO

SPEED UP SPARQL PROCESSING

Sven Groppe

Institute of Information Systems, University of Lübeck, Ratzeburger Allee 160, D-23562 Lübeck, Germany

Jinghua Groppe

Kahlhorststrasse 36a, D-23562 Lübeck, Germany

Volker Linnemann

Institute of Information Systems, University of Lübeck, Ratzeburger Allee 160, D-23562 Lübeck, Germany

Keywords: SparQL, RDF, Optimization, Index, Joins.

Abstract: SparQL is a query language developed by the W3C, the purpose of which is to query a data set in RDF

representing a directed graph. Many free available or commercial products already support SparQL

processing. Current index-based optimizations integrated in these products typically construct indices on the

subject, predicate and object of an RDF triple, which is a single datum of the RDF data, in order to speed up

the execution time of SparQL queries. In order to query the directed graph of RDF data, SparQL queries

typically contain many joins over a set of triples. We propose to construct and use an index of precomputed

joins, where we take advantage of the homogenous structure of RDF data. Furthermore, we present

experimental results, which demonstrate the achievable speed-up factors for SparQL processing.

1 INTRODUCTION

Semantic Web applications typically use the

Resource Description Format (RDF) (Brickley and

Guha, 2000) as data format. RDF data represents a

directed graph, which consists of triples (s, p, o),

where the subjects s and the objects o of the triples

describe the nodes of the directed graph and the

predicates p of the triples the arcs.

The World Wide Web Consortium (W3C)

develops SparQL (see (W3Ca, 2006), (W3Cb, 2006)

and (W3Cc, 2006)) as query language for RDF data,

which currently got the status of a candidate

recommendation.

The basic concept of SparQL queries are triple

patterns, where variables are bound to the subjects,

predicates or objects of triples of the RDF data, or

literals at the place of the subject, predicate or object

are constraints to the triples of the RDF data.

Common variables over two triple patterns express a

join and are the typical way to formulate a query in

order to retrieve a subgraph of the directed graph of

the RDF data.

In recent years, RDF storage systems, which

support or plan to support SparQL, have occurred

like Jena (Wilkinson et al., 2003), Sesame

(Broekstra, Kampman and van Harmelen, 2002),

rdfDB (Guha, 2006), Redland (Beckett, 2002),

Kowari (Northrop Grumman Corporation, 2006),

RDF Suite (Alexaki et al., 2001) and Allegro (Franz

Inc., 2006).

Many of these systems use an index in order to

faster access RDF data when executing SparQL

queries and thus speed up SparQL processing. In

comparison to the indices used in these systems, we

propose an index of precomputed joins in order to

speed up the execution of joins in SparQL queries.

We show by an experimental evaluation that

indices of precomputed joins are practical and speed

up SparQL processing.

We present our proposed approach in Section 2,

and we describe a performance analysis comparing

our approach with existing systems in Section 3.

Section 4 deals with the Related Work. We end up

with the summary and conclusions in Section 5.

Groppe S., Groppe J. and Linnemann V. (2007).

USING AN INDEX OF PRECOMPUTED JOINS IN ORDER TO SPEED UP SPARQL PROCESSING.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - DISI, pages 13-20

DOI: 10.5220/0002374900130020

 SciTePress

2 INDEX OF PRECOMPUTED

JOINS

We present a short introduction to RDF and SparQL

in Section 2.1. Section 2.2 describes how to use the

proposed index structure to answer SparQL queries

containing one join. Section 2.3 presents the

algorithm to construct the index. Section 2.4 extends

our approach to handle multiple joins over several

triple patterns.

2.1 Introduction to RDF and SparQL

RDF data (Brickley and Guha, 2000) contains a set

of triples (s, p, o), where s is called the subject of the

triple, p the predicate of the triple, and o the object

of the triple. The RDF data of Figure contains three

triples, the first of which associates

<http://example.org/book/book1> (the

subject) with

<http://purl.org/dc/elements/1.1/ti

tle> (the predicate) and "SPARQL Tutorial"

(the object).

SPARQL (see (W3Ca, 2006), (W3Cb, 2006) and

(W3Cc, 2006)) is a query language for retrieving

information from RDF graphs stored in semantic

storage systems. SparQL will be increasingly

important as query language for RDF as it has

recently reached a candidate recommendation of the

W3C. The outline query model is graph patterns

expressed by simple triple patterns. It does not use

rules and is not path based.

We briefly introduce SparQL by a simple

example. Figure shows a SPARQL query containing

one join to find those pairs of books and their titles,

which have the same title, from the RDF data. The

query consists of two parts, the SELECT clause and

the WHERE clause. The SELECT clause identifies

the variables to appear in the query results (here ?x,

?y and ?title). The result-bindings of the

variables must be distinct if the SELECT clause

contains the optional DISTINCT keyword as in the

example of Figure. The WHERE clause has two

triple patterns, “?x

<http://purl.org/dc/elements/1.1/ti

tle> ?title.” and “?y

<http://purl.org/dc/elements/1.1/ti

tle> ?title.”. The first position (?x and ?y

respectively) in the triple pattern represents the

constraints or bindings to variables for the subjects

in the RDF data. The second position (here it is the

literal

<http://purl.org/dc/elements/1.1/ti

tle> in both cases) contains the constraints or

bindings to variables for predicates of the triples of

the RDF data, and the third (here ?title for both

cases) contains the constraints or bindings to

variables for the objects of the triples of the RDF

data. The join of the query is expressed by using the

same variable ?title in both triple patterns.

This query is one of the simplest SparQL

queries. There are further constructs to e.g. filter the

results further by using comparison operators, use

built-in functions, and set operations like the

UNION operator. We refer the interested reader to

(W3Cc, 2006) for a complete list and description of

the SparQL features.

<http://example.org/book/book1>

<http://purl.org/dc/elements/1.1/title>

"SPARQL Tutorial" .

<http://example.org/book/book2>

<http://purl.org/dc/elements/1.1/title>

"SPARQL Tutorial" .

<http://example.org/book/book3>

<http://purl.org/dc/elements/1.1/title>

"Index" .

Figure 1: RDF data.

SELECT DISTINCT ?x,?y,?title

WHERE

{

<http://purl.org/dc/elements/1.1/title>

?title .

<http://purl.org/dc/elements/1.1/title>

?title .

}

Figure 2: SparQl query containing one join.

The query result (see Figure) is all the

combinations of pairs (x, y) of books with the same

title.

In this paper, we focus on those queries, which

contain one or more joins over different triple

patterns, i.e. we directly support the subset of

SparQL valid according to the following EBNF rule

Start.

Start ::= ”SELECT” “DISTINCT” var (“,” var)*

“WHERE” “{” triplePattern*

“}”.

triplePattern ::= (literal|var)

(literal|var)

(literal|var).

var ::= ”?” QName.

ICEIS 2007 - International Conference on Enterprise Information Systems

where literal represents a literal and QName

represents names.

X y title

<http://example.

org/book/book1>

<http://example.o

rg/book/book1>

“SPARQL

Tutoria

l”

<http://example.

org/book/book1>

<http://example.o

rg/book/book2>

“SPARQL

Tutoria

l”

<http://example.

org/book/book2>

<http://example.o

rg/book/book1>

“SPARQL

Tutoria

l”

<http://example.

org/book/book2>

<http://example.o

rg/book/book2>

“SPARQL

Tutoria

l”

<http://example.

org/book/book3>

<http://example.o

rg/book/book3>

“Index”

Figure 4: Result of the SparQL query of Figure with input

of Figure 1.

Note that our approach can be applied to more

complex SparQL queries, by first retrieving the

results of the joins by using our approach and then

restricting the result set by applying the operations

of the more complex SparQL constructs (e.g.

FILTER expressions).

2.2 Using the Index for Execution of a

SparQL Query with One Join Over

Two Triple Patterns

We first deal with constructing and using the index

of precomputed joins for one join over two triple

patterns. We extend the approach for indices of

precomputed joins for multi-joins over different

triple patterns in later sections.

SELECT DISTINCT ?x,?y,?title

WHERE

{

<http://purl.org/dc/elements/1.1/title>

?title .

<http://purl.org/dc/elements/1.1/title>

?y .

}

Figure 5: Second SparQL query containing one join,

which is equivalent to the third SparQL query in Figure 6.

SELECT DISTINCT ?x,?y,?title

WHERE

{

<http://purl.org/dc/elements/1.1/title>

?y .

<http://purl.org/dc/elements/1.1/title>

?title .

}

Figure 6: Third SparQL query containing one join, which

is equivalent to the second SparQL query in Figure 5.

Without considering symmetric cases, we have

to consider 9 different cases of joins in two triple

patterns (see Figure). See Figure and Figure for

examples of SparQL queries of the case 3 and of the

case 7 respectively. Note that at each place of the

subjects, predicates and objects of the two triple

patterns can be either a literal or a variable. Join-

partners are fixed by a common variable. The

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

(1)

(2) (3)

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

(4)

(5) (6)

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

(7)

(8) (9)

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p os p o

1.st Triple

Pattern

s p os p o

2.nd Triple

Pattern

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p os p o

1.st Triple

Pattern

s p os p o

2.nd Triple

Pattern

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p os p o

1.st Triple

Pattern

s p os p o

2.nd Triple

Pattern

(1)

(2) (3)

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p os p o

1.st Triple

Pattern

s p os p o

2.nd Triple

Pattern

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p os p o

1.st Triple

Pattern

s p os p o

2.nd Triple

Pattern

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p os p o

1.st Triple

Pattern

s p os p o

2.nd Triple

Pattern

(4)

(5) (6)

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p os p o

1.st Triple

Pattern

s p os p o

2.nd Triple

Pattern

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p os p o

1.st Triple

Pattern

s p os p o

2.nd Triple

Pattern

s p o

1.st Triple

Pattern

s p o

2.nd Triple

Pattern

s p os p o

1.st Triple

Pattern

s p os p o

2.nd Triple

Pattern

(7)

(8) (9)

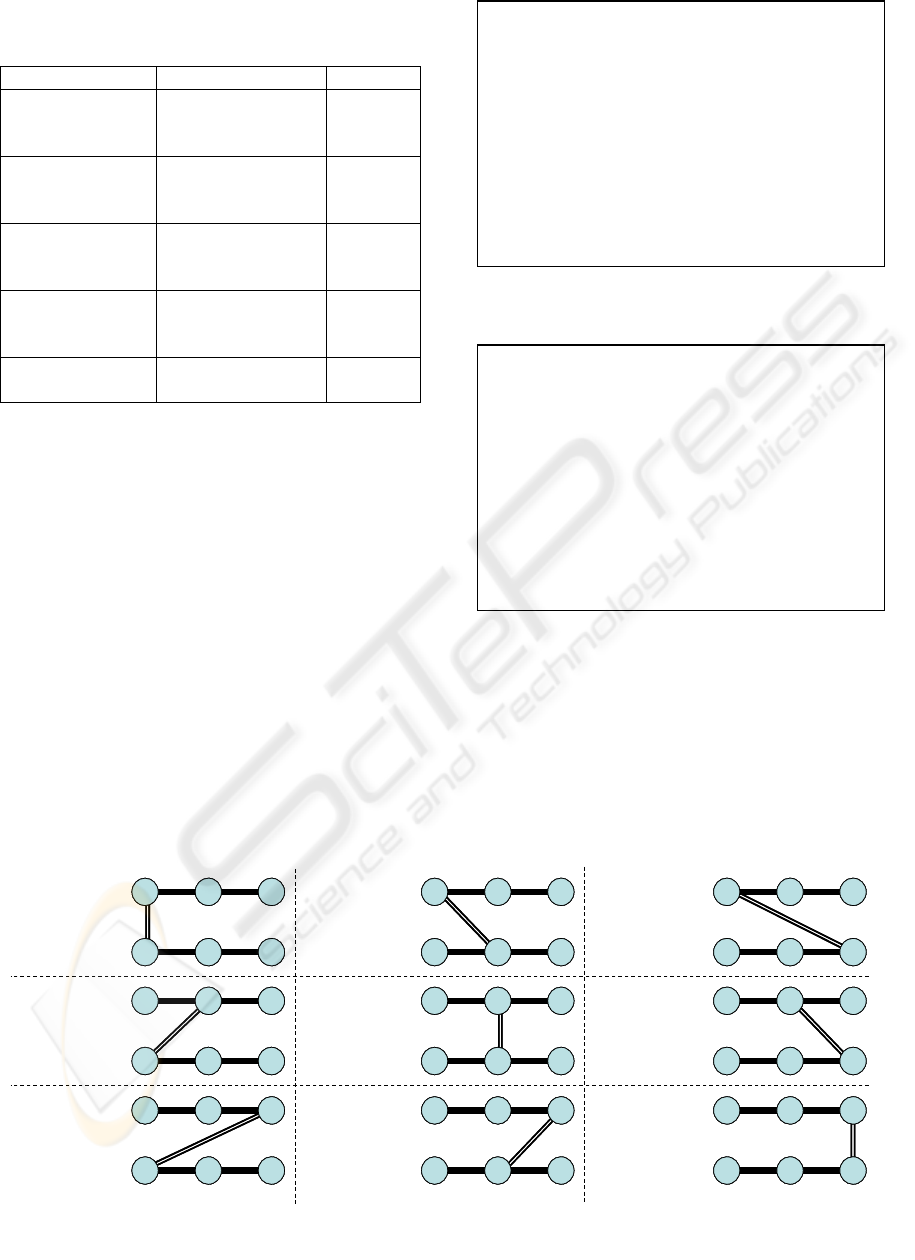
Figure 3: Different join cases for one join over two triple patterns.

USING AN INDEX OF PRECOMPUTED JOINS IN ORDER TO SPEED UP SPARQL PROCESSING

common variable of the two triple patterns

determines the different cases in Figure.

Note that the executions of the queries presented

in Figure and in Figure retrieve the same results for

the bindings of the variables. They are equivalent

queries except of the order of their triple patterns.

Thus, case 3 and case 7 (and analogously case 2 and

case 4, and case 6 and case 8) of Figure are

symmetric cases, where only the order of the triple

patterns are exchanged, which does not influence the

final result. Therefore, we only have to consider the

cases 1, 2, 3 5, 6 and 9, when we exchange the order

of triple patterns for the cases 4, 7 and 8.

Keys are unambiguous objects to identify the

entries in indices. Indices are data structures and

methods to administer pairs of keys and their

corresponding entries, which are here the results of

the joins. Especially the access to the entry by using

the key should be fast.

Variables in the triple patterns specify which of

the subjects, predicates and objects of two

considered triples of the RDF data are bound to the

variables. Literals in triple patterns are fixed

constraints in the triple patterns. Thus, the sequence

of literals of the two triple patterns is the key for the

triples of the RDF data. If we do not consider the

position of the literals in the triple patterns, we can

only ambiguously retrieve the relevant triples of the

RDF data, as we can retrieve in general the same key

for different constraints. For example, consider two

queries Q1 and Q2. Let us assume that Q1 has the

literals L1 and L2 at the subject and object position

of the first triple pattern, and Q2 has the literals L1

and L2 at the predicate and object position of the

second triple pattern. It is obvious that we should

retrieve different results for both queries, but we

determine the same key <L1, L2> from both queries

Q1 and Q2 and we are thus not able to distinguish

these results by the “key”. We propose to use

different indices for all possible situations of

positions of literals by determining the current index

from the positions of literals in the currently

considered query.

As we consider queries containing one join

expressed by a common variable, we only have to

consider four relevant positions in the two triple

patterns together. Figure contains the relevant

positions for the different join cases of Figure

(except the eliminated symmetric join cases 4, 7 and

8). Thus, we have to construct and use 2

=16

different indices for each join case of Figure except

the eliminated symmetric join cases 4, 7 and 8.

Therefore, we have to administer 6*2

=96 different

indices, which is practical as shown in the

experimental evaluation. We can determine the

index for a specific query by computing Σ

i=0

where B

=1 if there is a literal at the position i (see

Figure) in the considered triple patterns without the

join partners as declared in Figure, otherwise B

is 0.

Position 0 Position 1 Position 2 Position

Case 1 p1 o1 p2 o2

Case 2 p1 o1 s2 o2

Case 3 p1 o1 s2 p2

Case 5 s1 o1 s2 o2

Case 6 s1 o1 s2 p2

Case 9 s1 p1 s2 p2

Figure 7: The relevant positions 0 to 3 for the join cases of

Figure 3 except the eliminated symmetric cases, where sx

represents the subject position, px the predicate position

and ox the object position in triple pattern x∈{1, 2}.

After the determination of the correct index, we

can access the correct triple set for the two triple

patterns in the index by using the key o

i=0

, where

o is the concatenation operator for keys and L

is the

literal at the position i (see Figure) in the considered

triple patterns if there is a literal, otherwise L

is the

empty key. For example, we compute the key

“<

http://purl.org/dc/elements/1.1/title>|<ht

tp://purl.org/dc/elements/1.1/title>

” from

the query of Figure.

When using a hash map as index, we can retrieve

the results of a join over two triple patterns in

constant time.

If there are two or three joins in two triple

patterns, then we can use the index for one join and

additionally compare the constraints of the second or

third on the retrieved triple set, or construct and use

also indices for these (more seldom) cases.

If there are two or more joins over more than

two different triple patterns, one approach is to split

the joins into several (part) joins over two triple

patterns, access their results separately by using our

approach, each access saves the processing time of

one join, and then joining the results.

Another approach is to extend our approach for

multi-joins over different triple patterns, which we

present in Section 2.4.

2.3 Constructing the Index

In order to construct the index from the input RDF

data, we first construct three indices to access the

triples of common subjects, predicates and objects.

For this purpose, we iterate one time through all

triples of the input RDF data set and add the current

triple into three hash maps, where we use the subject

as key for the first hash map, the predicate as key for

the second hash map, and the object as key for the

third hash map. Note that these hash maps not only

store one triple for one key, but a list of triples with

these keys. The construction of each of these three

ICEIS 2007 - International Conference on Enterprise Information Systems

hash maps can be done in O(n), where n is the

number of triples in the input RDF data set.

Furthermore, note that these three indices could be

also used to retrieve the corresponding triples of one

triple pattern of a query, where the key is one literal

at the subject, predicate or object position of the

triple.

Hash-

entry

for

First Triple Second Triple

<http://example.o

rg/book/book1>

<http://purl.org/

dc/elements/1.1/t

itle>

“SparQL Tutorial”

<http://example.o

rg/book/book1>

<http://purl.org/

dc/elements/1.1/t

itle>

“SparQL Tutorial”

<http:/

/exampl

e.org/b

ook/boo

k1>

<http://example.o

rg/book/book1>

<http://purl.org/

dc/elements/1.1/t

itle>

“SparQL Tutorial”

<http://example.o

rg/book/book2>

<http://purl.org/

dc/elements/1.1/t

itle>

“SparQL Tutorial”

<http://example.o

rg/book/book2>

<http://purl.org/

dc/elements/1.1/t

itle>

“SparQL Tutorial”

<http://example.o

rg/book/book1>

<http://purl.org/

dc/elements/1.1/t

itle>

“SparQL Tutorial”

<http:/

/exampl

e.org/b

ook/boo

k2>

<http://example.o

rg/book/book2>

<http://purl.org/

dc/elements/1.1/t

itle>

“SparQL Tutorial”

<http://example.o

rg/book/book2>

<http://purl.org/

dc/elements/1.1/t

itle>

“SparQL Tutorial”

<http:/

/exampl

e.org/b

ook/boo

k3>

<http://example.o

rg/book/book3>

<http://purl.org/

dc/elements/1.1/t

itle>

“Index”

<http://example.o

rg/book/book3>

<http://purl.org/

dc/elements/1.1/t

itle>

“Index”

Figure 8: Example for the constructed hash map for the

case of join case 9 (see Figure 3) and for the position of

one literal at the subject position of the first triple pattern,

where the input RDF data is presented in Figure 1.

Afterwards, we construct the 6*2

=96 different

indices by initializing one hash map containing lists

of pairs of triples as entries for each different index

representing one case of join partners and positions

of literals in the considered two triple patterns.

We iterate again through all triples of the input

RDF data set. We consider recursively all cases of

join partners and positions of literals and determine

the possible second triples in constant time by using

the hash maps, where the key is either the subject,

predicate or object of the triple.

Figure contains an example for the constructed

hash map for the case of join case 9 (see Figure) and

for the position of one literal at the subject of the

first triple pattern, where the input RDF data is

presented in Figure.

The construction of each of these 96 different

indices can be done in O(n

), where n is the number

of triples in the input RDF data set, as we iterate one

time through all triples in the input RDF data set and

for each triple, we add at most n different triples to

the considered index.

Note that the construction of the index is done

only once after reading the input RDF data set and

does not need to be repeatedly done for each query.

Then a join over two triple patterns of a query can be

determined within constant time.

2.4 Extending the Approach for Multi-

Joins over Multiple Different Triple

Patterns

We extend now our approach for multi-joins over

multiple different triple patterns.

We consider now n-1 joins between n triple

patterns (see Figure).

We can express these n-1 joins by a sequence

, …, x

2*(n-1)

>, where x

2*(i-1)

∈{1,2,3} indicates the

join partner (1=subject, 2=predicate and 3=object) of

the i-th triple pattern of the join with the previous

triple pattern i-1, and x

2*(i-1)+1

∈{1,2,3} indicates the

join partner of the i-th triple pattern of the join with

the following triple pattern i+1. Thus, we have

2*(n-1)

different cases for joins between these n triple

patterns including those cases, which are equivalent

except of the order of their triple patterns. The

symmetric cases are those cases, where for all i∈{1,

…, n-1}:x

2*(n-1)+1-i

. Therefore, the number of

symmetric cases is 3

n-1

. Altogether, the number of

joins without those cases, which are equivalent

except of the order of their triple patterns, is half of

Figure 9: n-1 joins over n different triple patterns.

USING AN INDEX OF PRECOMPUTED JOINS IN ORDER TO SPEED UP SPARQL PROCESSING

all cases without the symmetric cases plus the

symmetric cases, i.e. (3

2*(n-1)

-3

n-1

)/2 + 3

n-1

*(1/2)*(3

n-1

+1).

The number of literal and variable positions

without those positions of the join partners is at most

2 for every triple pattern. Thus, we have at most 2

n*2

positions, which are bounded or unbounded and

which have to be considered in a separate index

each.

Altogether, we have to administer

n*2

*(3

n-1

*(1/2)*(3

n-1

+1)) indices for n-1 joins

between n triple patterns, which is not practical for

n≥3. Future work will cover approaches to reduce

the number of indices used for multi-joins over

different triple patterns. Furthermore, future work

will cover to develop disk-based indices, where we

can access the entry of a hash index with one disk-

access. Also incremental indices, where we

incrementally extend the index whenever we

compute a new join, such that we avoid the time-

consuming initialization of the indices and where

only those joins are computed, which are really

needed, is on the agenda of future work.

3 PERFORMANCE EVALUATION

We present the experimental evaluation in this

section. We describe the experimental environment

in Section 3.1 and present the experimental results in

Section 3.2.

3.1 Experimental Environment

The test system for all experiments is a 2 Gigahertz

Intel Pentium M processor with 1 Gigabytes main

memory, where we use Windows XP as operation

system and Java version 1.5. Furthermore, we use

Jena (Wilkinson et al., 2003) and Allegro (Franz

Inc., 2006) as RDF storage systems to compare the

results of our approach with those of existing

systems.

3.2 Experimental Results

We have generated RDF data in XML representation

with 1, 200, 400, 600, 800 and 1000 triples. We have

generated RDF data, where (a) no predicates of the

triples are the same, and (b) 25% of the predicates

are the same. For an example, see Figure for 10

triples with 25% same predicates. The used SparQL

query is represented in Figure, which is a query of

join case 5, where we do not have any literals in the

query.

<http://groppe.org/elem1>

<http://groppe.org/elem0>

<http://groppe.org/elem1>.

<http://groppe.org/elem2>

<http://groppe.org/elem0>

<http://groppe.org/elem2>.

<http://groppe.org/elem3>

<http://groppe.org/elem3>.

<http://groppe.org/elem4>

<http://groppe.org/elem4>.

<http://groppe.org/elem5>

<http://groppe.org/elem5>.

<http://groppe.org/elem6>

<http://groppe.org/elem6>.

<http://groppe.org/elem7>

<http://groppe.org/elem7>.

<http://groppe.org/elem8>

<http://groppe.org/elem8>.

<http://groppe.org/elem9>

<http://groppe.org/elem9>.

<http://groppe.org/elem10>

<http://groppe.org/elem10>.

<http://groppe.org/elem1>

<http://groppe.org/elem0>

<http://groppe.org/elem1>.

Figure 10: Generated RDF data for number of elements 10

and 25% elements with the same predicate.

Figure represents the time used to load the

RDF/XML input files into the Jena and Allegro

system, and Figure 13 represents the time used by

our approach to construct the index. Figure 14

contains the number of elements of the result set of

the query of Figure 11. Figure 15, Figure 16 and

Figure 17 represent the execution times of the Jena

evaluator, the Allegro system and our approach for

the SparQL query of Figure. Our approach is the

fastest and needs less than 1 millisecond for the

query for all different input RDF/XML files. The

Allegro system needs most time and already

generates out-of-memory errors for input files with

400 triples. Note that the Allegro system provides a

client server system, where the data has to be

transferred from the server to the client even in the

case that the client and the server run on the same

computer. Thus, in comparison to the Jena evaluator

and our approach, using the Allegro system needs to

iterate at least one time through the whole result set,

which we neglect when using the Jena evaluator and

our approach.

ICEIS 2007 - International Conference on Enterprise Information Systems

Select DISTINCT * where

{

?x ?y ?z.

?a ?y ?b.

}

Figure 11: Used SparQL query in the experiments.

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

Time in

se conds

1 200 400 600 800 1000

Number of Elements

Jena

Allegro

Figure 12: Time used to load RDF/XML input file.

Figure 13: Time used to construct the index for 0% and

25% same predicates in the input RDF data.

4 RELATED WORK

(Matono et al., 2003) presents an indexing scheme

for RDF and RDF Schema based on Suffix Arrays of

determined path expressions, which represent the

data (and schema). Whereas the search for the

optimized execution of SparQL queries in the suffix

arrays require runtime O(log

(n+1)), our approach

accesses the results of joins in constant time O(1).

(Barton, 2004) generates a forest of trees annotated

with additional information at those nodes of the

original RDF data, which do not fulfil the forest

requirement (and lead to a graph). However, the

approach is used to find possible paths between two

given nodes and thus is not directly usable for

SparQL processing in the form it has been proposed.

(Becket, 2002), (Stuckenschmidt et al., 2004)

and (Harth and Decker, 2005) present the used

indices for different RDF storage systems. However,

they only consider indices over triples and not over

two or more triples containing a join.

In comparison to all other approaches, we focus

on the optimized execution of SparQL queries with

one or more joins.

Time in

se co nd s

1 200 400 600 800 1000

Number of Elements

25%

500

1000

1500

2000

2500

Time in

se cond s

1 200

Number of Elements

25%

Figure 17: Execution times of the Allegro system for

0% and 25% same predicates in the input RDF data.

0,01

0,02

0,03

0,04

0,05

0,06

0,07

Time in

seconds

1 200 400 600 800 1000

Number of Elements

Jena

Our Approach

Figure 16: Execution times of Jena in comparison to

our approach for input data with 25% same predicates.

100000

200000

300000

400000

500000

600000

700000

Size of Result

in Number of

Triple Pairs

1 200 400 600 800 1000

Number of Elements

25%

Figure 14: Number of elements in the result set for 0% and

25% same predicates in the input RDF data.

USING AN INDEX OF PRECOMPUTED JOINS IN ORDER TO SPEED UP SPARQL PROCESSING

5 SUMMARY AND

CONCLUSIONS

SparQL seems to be the upcoming query language

for RDF data. Queried subgraphs of the input RDF

data are formulated by using joins over single triple

patterns. In this paper, we focus on the optimization

of the execution of joins in SparQL queries by using

indices. After the construction of the indices, we can

access the result for one join over two triple patterns

of the query in constant time, when using hash maps

for the indices.

In the performance evaluation, we compare the

results of the execution times of our prototype with

the execution time of existing systems.

Future work covers to use a disk-based index,

approaches to reduce the number of indices,

incremental indices and advanced techniques for

indices of precomputed multi-joins over several

triple patterns.

REFERENCES

Alexaki, S., Christophides, V., Karvounarakis, G.,

Plexousakis, D., and Tolle, K., 2001. The rdfsuite:

Managing voluminous rdf description bases. In

Proceedings of the 2

International Workshop on the

Semantic Web (SemWeb’01) in conjunction with

WWW, Hongkong.

Barton, S., 2004. Designing Indexing Structure for

Discovering Relationships in RDF Graphs, Dateso

2004.

Beckett, D., 2002. The design and implementation of the

Redland RDF application framework. Computer

Networks, 39(5):577-588.

Bertino, E., 1991. An Indexing Technique for Object-

Oriented Languages. In Proceedings of the 7

International Conference on Data Engineering, IEEE

Computer Society, Kobe, pages 160-170.

Brickley, D., Guha, R. V., 2000. Resource description

framework specification.

Broekstra, J., Kampman, A., van Harmelen, 2002.

Sesame: A Generic Architecture for Storing and

Querying RDF and RDF Schema. In Proceedings of

the 2

International Semantic Web Conference,

Springer, Sardinia.

Franz Inc., 2006. AllegroGraph 64-bit RDFStore,

http://www.franz.com/products/allegrograph.

Guha, R., 2006. rdfDB: An RDF Database,

http://www.guha.com/rdfdb.

Harth, A., Decker, S., 2005. Optimized Index Structure for

Querying the Web. In Third Latin American Web

Congress (LA-WEB 2005), Buenos Aires, Argentina.

Matono, A., Amagasa, T., Yoshikawa, Uemura, S., 2003.

An Indexing Scheme for RDF and RDF Schema based

on Suffix Arrays. In Proceedings of the 1

International Workshop on Semantic Web and

Databases (SWDB’03) co-located with VLDB 2003,

Berlin.

Northrop Grumman Corporation, 2006. Kowari,

http://www.kowari.org.

Stuckenschmidt, R., Vdovjak, R., Houben, G.-J.,

Broekstra, J., 2004. Index Structures and Algorithms

for Querying Distributed RDF Repositories. In

Proceedings of 13

InternationalWorld Wide Web

Conference, New York.

Wilkinson, K., Sayers, C., Kuno, H. A., Reynolds, D.,

2003. Efficient RDF Storage and Retrieval in Jena2. In

Proceedings of the 1

International Workshop on

Semantic Web and Databases (SWDB’03) co-located

with VLDB 2003, Berlin.

W3Ca, 2006. SPARQL Query Language for RDF, W3C

Candidate Recommendation, 6 April 2006.

W3Cb, 2006. SPARQL Query Results XML Format, W3C

Candidate Recommendation, 6 April 2006.

W3Cc, 2006. SPARQL Protocol for RDF, W3C Candidate

Recommendation, 6 April 2006.

ICEIS 2007 - International Conference on Enterprise Information Systems