INVESTIGATIONS ON OBJECT-CENTERED ROUTING IN

DYNAMIC ENVIRONMENTS: ALGORITHMIC FRAMEWORK AND

INITIAL NUMERICAL RESULTS

Support for Distributed Decision Making in Transport Systems

Bernd-Ludwig Wenning, Carmelita G

org, Andreas Timm-Giel

Communication Networks, University of Bremen, Otto-Hahn-Allee, D-28359 Bremen, Germany

orn Sch

onberger, Herbert Kopfer

Chair of Logistics, University of Bremen, Wilhelm-Herbst-Straße 5, 28359 Bremen, Germany

Keywords:

Autonomous decision making, transport planning, route request / route reply, dynamic decision problem,

stochastic problem data.

Abstract:

Dynamics in logistics are a subject of increasing importance in logistic processes. The more detailed dy-

namics are considered, the more complicated it becomes to handle them in centralized planning. Therefore,

decentralized approaches with autonomous cooperating entities might become more efﬁcient.

This paper introduces some aspects of decentralized approaches, mainly focusing on the process of information

acquisition which enables the autonomous entities to decide about the handling of routes and orders.

1 INTRODUCTION

The consideration of so-called

dynamics

which are

process relevant up-to-date and so far not known in-

formation appearing consecutively and unpredictably

with ongoing time, is of increasing importance for the

management of transport processes in today’s logistic

systems.

Two aspects of dynamics are recognized. At ﬁrst,

transport networks are formed temporarily and by in-

dependent parties each providing an own subnetwork.

A centralized knowledge about the complete network

is typically not available. Secondly, a very huge

amount of up to date information that is exploited

in the management of the transport processes requir-

ing frequent process updates and adaptations in order

to keep the transport quality on a maximum efﬁcient

level.

The application of centralized planning ap-

proaches is impossible. Decision support systems

have to be able to support an object-centered plan-

ning, in which several autonomous objects have to be

coordinated instead of determining the exact process

for each vehicle.

In Section 2, an example of such a scenario is

introduced. Section 3 is about the conﬁguration

of generic algorithmic support for the decentralized

routing and the proposed decision support is assessed

within a simulation study in Section 4.

2 CHALLENGE OUTLINE

This section is dedicated to the outline of the decision

situation we are dealing with. Subsection 2.1 provides

a short survey about the relevant streams in the scien-

tiﬁc literature. The investigated network is introduced

in Subsection 2.2. An explicit scenario is shown in

Subsection 2.3.

2.1 Literature

Two general approaches for coping with dynamics in

routing have been discussed in the scientiﬁc literature.

a-priori optimization

a set of a-priori-paths is

determined in advance that visits all possible cus-

tomer sites (Powell et al., 1995). The a-priori-paths

have the least expected costs among all possible

paths. If determining the paths, probability distribu-

tions about the need for visiting a particular customer

site are exploited. The a-priori-routes are then up-

dated and adapted to the real need, e.g. if it turns

225

Wenning B., Görg C., Timm-Giel A., Schönberger J. and Kopfer H. (2007).

INVESTIGATIONS ON OBJECT-CENTERED ROUTING IN DYNAMIC ENVIRONMENTS: ALGORITHMIC FRAMEWORK AND INITIAL NUMERICAL

RESULTS - Support for Distributed Decision Making in Transport Systems.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 225-230

DOI: 10.5220/0002379502250230

 SciTePress

out that a customer site does not need to be visited, it

might be skipped from the a-priori-route but the vis-

iting order of the remaining requests is not subject to

alternation. A-priori-optimization-based approaches

require the knowledge about a suitable probability

distribution.

reactive routing

approaches, only known prob-

lem data about customer sites and the network struc-

ture are considered during the generation of routes.

After an event has been detected that corrupts the re-

alization of the so far followed routes, a new route

generation is carried out. Route-update times are de-

termined in advance in

rolling horizon planning

(Bi-

tran and Tirupati, 1993), but in

online planning

(Irani

et al., 2004; Fiat and Woeginger, 1998), a new plan-

ning is executed every time a new event appears that

contradicts the execution of the so far valid routes.

(Langer et al., 2007) investigate different algorithmic

paradigms for their ability to support a quick and re-

liable decision making in dynamic routing.

Impacts of autonomously made decisions in a net-

work are analysed and evaluated in (Roughgarden,

2005).

2.2 Dynamic Network Routing

Challenge

A transport system is considered that is used to ful-

ﬁl transport demands using a collection of vehicles.

The demand is expressed by customer requests which

are speciﬁed consecutively over time. Since the vehi-

cles are allowed to decide autonomously about their

operations, a centralized planning model/solver com-

bination cannot be deployed to tackle the problem.

As soon as a new request r is waiting to be sched-

uled, the existing autonomously deciding vehicles

check whether and how they are able to fulﬁl this re-

quest. In case that the vehicle v is interested to ful-

ﬁll this request it generates a route proposal r(v) =

, . . . , n

N(v,r)

) satisfying the following constraints.

1. Neither the vehicle capacity is exceeded nor re-

quest associated time windows are violated and

2. the vehicle returns to its home base not later than

a given time.

It is speciﬁed that a vehicle does not formulate

a proposal for request r when it is not able to fulﬁl

this request satisfying the two conditions mentioned

above.

The vehicles’ proposals then are compared and the

best proposal (according to current decision criteria)

is executed.

Beside additional requests, varying transshipment

or pickup as well as unloading times might be con-

sidered as a source of dynamics. Furthermore, trafﬁc

congestions inﬂuence the travel time required for us-

ing a connection between two adjacent locations.

Let t denote the time in which an event becomes

known that requires a new route determination. The

underlying graph in which a route has to be deter-

mined is deﬁned as

G (t) := (N (t), A (t), D (t)). The

node set

N (t) := N

∪

(t) consists of the static

set of network locations

and the current vehicle

positions collected in

(t). The nodes are con-

nected by the arcs collected in

A (t) (some arcs might

also represent roads that are temporarily closed). The

evaluation of a route proposal is done by applying

the evaluation function

D (t) to the nodes and arcs in-

volved in the considered route. The evaluation has to

be performed for each route proposal individually as

the travel times are not constant, but may vary with

ongoing time t due to trafﬁc congestions and high

workload in the pickup or delivery nodes.

The request r released at time t requires the trans-

port of a good of a certain capacity c

from a pickup

location p

∈

G (t) to a delivery location p

−

∈ G (t).

A route proposal has to start at the current vehicle po-

sition, passing p

and afterwards p

−

and terminat-

ing at a node in

G (t). Therefore, for each vehicle a

constrained shortest path problem in

G (t) has to be

solved (K

ohler et al., 2005).

2.3 Scenario Description

The scenario used here for the investigation of dy-

namic logistic networks is based on a map of Ger-

many. 18 major german cities have been selected as

nodes in the network, and edges are deﬁned according

to main highway connections as depicted in Figure 1.

At each of the nodes, transport orders for goods of

unit size are generated randomly during runtime, and

the generation rate is dependent on the size of the city,

ranging from 2 orders per hour in Kassel to 34 orders

per hour in Berlin. A basic version of this scenario has

been described in (Wenning et al., 2007), the version

used here has some slight modiﬁcations, which are a

different amount and distribution of vehicles and the

occurence of trafﬁc jams which is described in section

4.2.

The vehicles in this scenario have a capacity of

60 size units and a travel time limit of 8 hours be-

fore returning to their home location. This implies

they cannot cross the whole map, and transshipments

are required for transport orders that have to cover a

long distance. The amount as well as the distribution

of vehicles is subject to alteration between simulation

runs in order to increase the efﬁciency of transport

processes.

ICEIS 2007 - International Conference on Enterprise Information Systems

226

Berlin

Hamburg

München

Köln

Frankfurt

Dortmund

Stuttgart

Düsseldorf

Bremen

Duisburg

Hannover

Nürnberg

Dresden

Leipzig

Bielefeld

Bonn

Mannheim

Kassel

Figure 1: The simulated transport network.

3 ALGORITHMIC APPROACH

The conﬁguration of a reactive route ﬁnding proce-

dure is subject of this section. Since the events that

cause the update of the routes and the generation of

new proposals do not follow any known probabil-

ity distribution, an a-priori-optimization is far away

from applicability so that only a reaction on a route-

corruption event remains as a remedy.

The application of existing shortest path detect-

ing algorithms is compromised by the different con-

straints that restrict the set of realizable routes in the

considered scenario. In order to apply for example

Dijkstra-based methods to identify a feasible route, a

network pre-processing has to be carried out that re-

quires the knowledge of the complete network. As

stated in the introductory section, this assumption is

not valid and consequently, another approach has to

be used.

As it is assumed that probability distributions for

the considered events are not known to the compo-

nents of the dynamic scenario, routes have to be deter-

mined reactively. Therefore, a reactive two-step route

proposal generation is carried out. In the ﬁrst step,

possible routes to the designated termination node

of the vehicle’s route are identiﬁed using a network

broadcasting method. In the second step, all route op-

tions are evaluated and the highest valued route is se-

lected as the proposal of the considered vehicle (Sub-

section 3.1). For the explicit scenario introduced in

2.3, a special conﬁguration for this algorithm idea is

proposed (Subsection 3.2).

3.1 Route Request / Route Reply -

Methods

In the approach proposed here, a distributed routing

based on reactive mechanisms from communication

networks is transferred to the application in logistics.

The vehicles need to collect information on the cur-

rent network structure in order to make reasonable

and sensible routing decisions. Here, each node in

the network only knows its adjacent nodes but other

information is not available (cf. Section 1). In partic-

ular, this is information about the links (arcs) to the

adjacent nodes and available waiting packages at the

nodes corresponding to so far unserved requests.

The access to this information is similar to the

route discovery mechanisms in ad hoc networks, for

example in Dynamic Source Routing (DSR) (Johnson

and Maltz, 1996): The initiator (in this case a vehicle)

sends a request to its adjacent node. From there, this

request is propagated to the neighbour nodes. Each

node adds some of its local knowledge about the cur-

rent status to the request so that the request is accu-

mulating information as it propagates. When it has

reached a termination node, a reply is generated con-

taining all information that was collected on the way

and is sent back to the initiator. The initiator compares

the identiﬁed routes and selects the most appropriate

one as its route proposal.

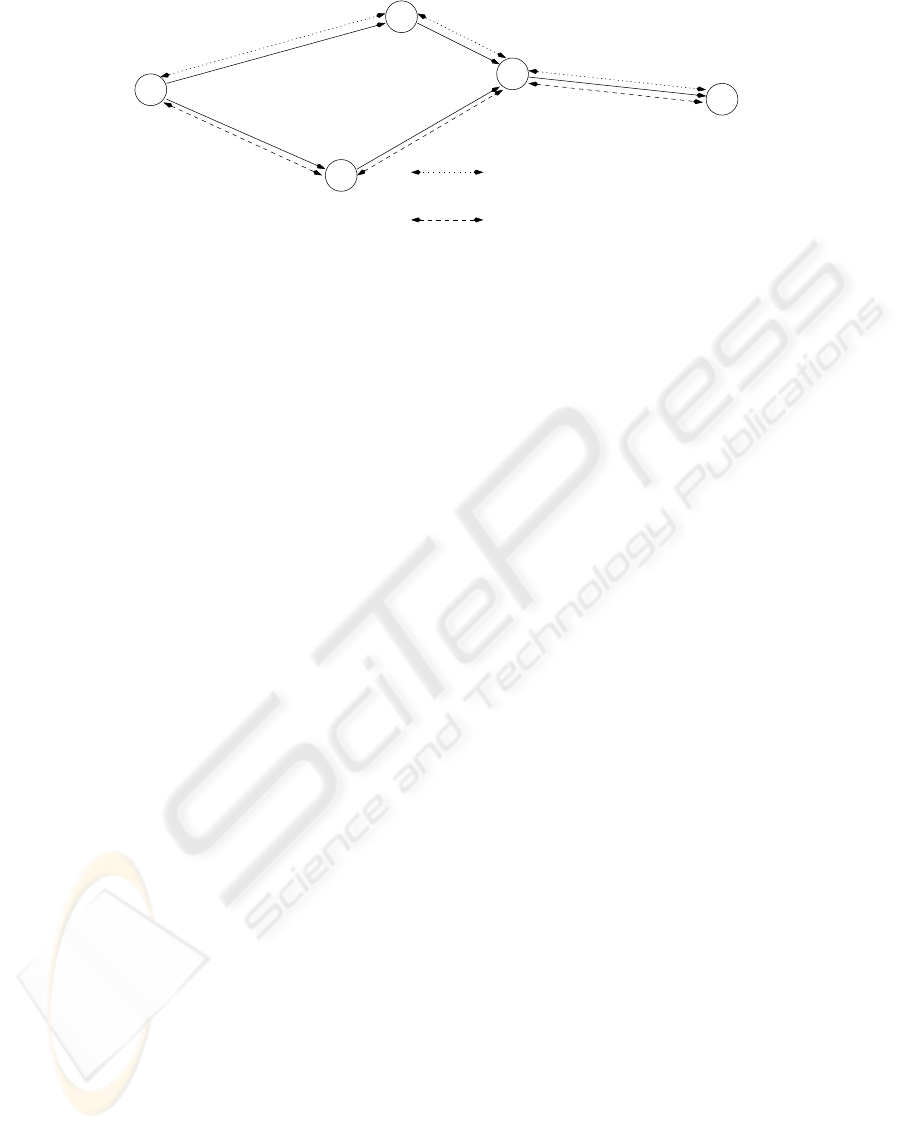
In the example illustrated in Fig. 2, the vehicle

waiting at node S needs a route to node T through the

current network

G (t) (which, in this example, is spec-

iﬁed by the solid arcs and the nodes S, 1, 2, 3 and T).

It starts the route discovery process by sending a route

request to S, which broadcasts it to its neighbours. In

the considered example, it sends the request to node

1 (dotted line) and to node 2 (dashed line). Neither 1

nor 2 coincide with the target node T so that 1 as well

as 2 forward the request to their neighbour 3. Again, 3

is not the target node and both incoming requests are

proceeded to the next neighbour now reaching the tar-

get node T. Two routes from S to T are found: route

A (S-1-3-T) and route B (S-2-3-T). T now sends a

reply to each of the requests, integrating information

that was added by the intermediate nodes during the

request forwarding phase.

The numbers in brackets represent the evaluation

values

D (t) for passing the associated arc or node.

Therefore, route A is evaluated by 5+0+2+0+7=14

and route B is evaluated by 6+0+4+0+7=17. Route

A would become the proposal of the considered vehi-

cle if the evaluation values represent costs.

3.2 Conﬁguration

In the simulation experiments described in the next

section, the vehicles in the scenario apply a rout-

ing method that is derived from source routing ap-

proaches in communication networks, such as the

aforementioned DSR. The knowledge about transport

INVESTIGATIONS ON OBJECT-CENTERED ROUTING IN DYNAMIC ENVIRONMENTS: ALGORITHMIC

FRAMEWORK AND INITIAL NUMERICAL RESULTS - Support for Distributed Decision Making in Transport Systems

227

(5)

(0)

(2)

(7)

(6)

(4)

route request / route reply A

route request / route reply B

Figure 2: Example for route request / route reply.

orders is limited to the locally available orders, and

knowledge about the network, especially estimated

travel times, are collected from distant nodes using

the described route request/route reply methods.

Before starting the routing process, a destination

node has to be found. The determination of this des-

tination node is done by counting the destinations of

the local transport orders and selecting the node as

destination that is most frequently requested. After

having obtained a route by receiving route replys, the

vehicle evaluates whether it is possible to cover the

route completely within its time constraints. If this is

not possible, the route is shortened up to a length that

does not violate the vehicle’s time constraints. The

most distant node then becomes a transshipment lo-

cation for the transport order.

4 NUMERICAL EXPERIMENTS

Results achieved from numerical experiments are re-

ported in this section. Initially, the experimental setup

is stated (Subsection 4.1). Afterwards, some nu-

merical results are presented and discussed (Subsec-

tion 4.2).

4.1 Experimental Setup

The simulation is done with the help of a simula-

tion environment developed for the simulation of au-

tonomous controlled logistics. This environment is

based on the Communication Networks Class Library

(CNCL), which is a discrete-event simulation library

originally intended for simulation of communication

networks and, with some extensions, is now also used

for the simulation of logistics. A more detailed de-

scription of the simulation environment is given in

(Becker et al., 2006).

The simulation scenario is speciﬁed as described

in section 2.3, the vehicles are selecting their routes,

according to the description in 3.2, by determining

the most requested destination and discovering a route

with the aforementioned route discovery scheme.

4.2 Presentation and Discussion of the

Results

This section presents results of simulations of three

different variations of the scenario with respect to dy-

namics, especially trafﬁc jams:

1. Free trafﬁc ﬂow, i.e. no trafﬁc jams are present for

the whole simulation time.

2. Trafﬁc jams appear randomly between Hannover

and Kassel with a jam probability of 0.2 and an

average vehicle delay of 1.5 hours when being

stuck in a trafﬁc jam. The vehicles have no knowl-

edge about the trafﬁc jams.

3. Same as 2. except for the vehicles having knowl-

edge about the trafﬁc jams.

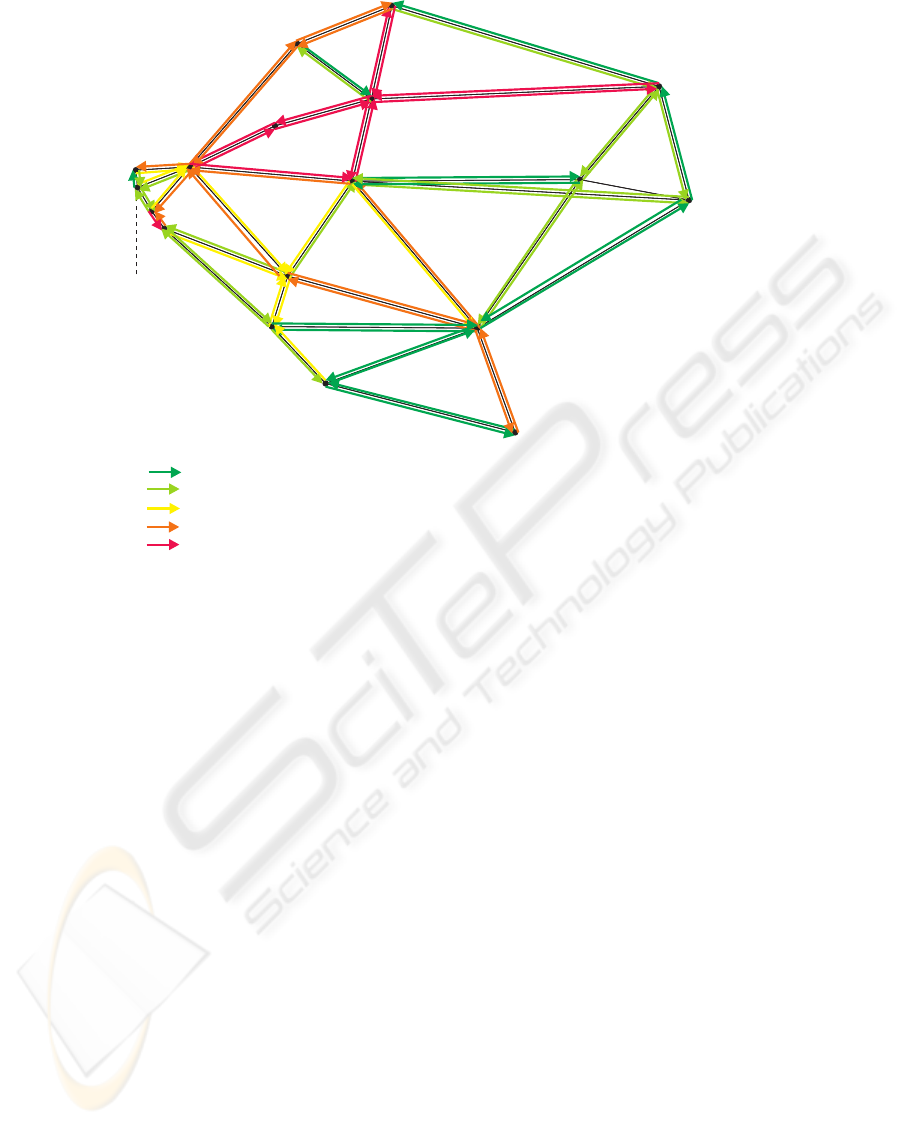
Figure 3 graphically shows the trafﬁc ﬂow in the

ﬁrst case. No trafﬁc jams are present, and some main

connections can be identiﬁed. 20 vehicles are the

minimum amount which is necessary to handle the

transport demand in this case, and their average ca-

pacity utilisation is 57.5%.

In the second case, trafﬁc jams are introduced on

a central and highly utilized part of the road network,

the connection between Hannover and Kassel. As the

vehicles had no knowledge of the trafﬁc jams, they

were planning their routes as if all roads were free.

The effect was that, when the number of vehicles was

not changed, some locations in the network were not

served frequently enough any more, causing the com-

plete scenario to become unstable with continuously

growing package stocks and delivery delays. To coun-

teract this effect, the number of vehicles in the sce-

nario had to be increased to 23, while their capacity

ICEIS 2007 - International Conference on Enterprise Information Systems

228

< 250

250 ... 400

400 ... 650

650 ... 1000

> 1000

Hamburg

Bremen

Dortmund

Duisburg

Berlin

Hannover

Leipzig

Dresden

Nürnberg

Kassel

München

Stuttgart

Düsseldorf

Köln

Frankfurt

Mannheim

Bonn

Number of trips on edge

Bielefeld

Figure 3: Usage of edges without appearance of trafﬁc jams.

utilisation went down to 50.1%. Figure 4 shows the

trafﬁc ﬂow in this scenario. It can be seen that there

is more trafﬁc in the northern/northwestern part of the

map, which matches the fact that all additional vehi-

cles were added to the Hamburg node.

When, in case 3, the vehicles had knowledge

about the jams, it was possible to reduce the num-

ber of required vehicles back to 20, resulting in traf-

ﬁc ﬂows very similar to Figure 3 again, yet with a

slightly higher vehicle capacity utilisation than with-

out the trafﬁc jams (58.1% vs. 57.5%). This proves

the knowledge about current dynamics improves the

performance of object-centric routing in the scenario.

It enables the vehicles to adapt their routing to the

changed road conditions, thus improving the efﬁ-

ciency of the overall system.

The results shown here are initial results for one

approach to implement autonomous control into lo-

gistic components. There are other approaches which

have been investigated (Wenning et al., 2006) or are

currently under investigation, all of them based on

the idea of transferring concepts from communication

networks to logistics.

5 CONCLUSIONS AND

OUTLOOK

This paper has introduced important aspects of a de-

centralized planning approach for logistics. This ap-

proach relies on a mechanism that collects informa-

tion about the current state of the dynamic environ-

ment similarly to route discovery processes in com-

munication networks. It has been shown in simula-

tion results that knowledge about the current state im-

proves the performance of the logistic system by util-

ising resources more efﬁciently.

The authors are currently continuing their research

on object-centered routing in several directions: be-

sides the further work on suitable algorithms, one fo-

cus is to achieve comparability to traditional logisti-

cal routing approaches, another is to even include the

load as active participant with decision capabilities in

the routing process.

ACKNOWLEDGEMENTS

This research was supported by the German Research

Foundation (DFG) as part of the Collaborative Re-

INVESTIGATIONS ON OBJECT-CENTERED ROUTING IN DYNAMIC ENVIRONMENTS: ALGORITHMIC

FRAMEWORK AND INITIAL NUMERICAL RESULTS - Support for Distributed Decision Making in Transport Systems

229

<250

250...400

400...650

650...1000

>1000

Hamburg

Bremen

Bielefeld

Dortmund

Duisburg

Berlin

Hannover

Leipzig

Dresden

Nürnberg

Kassel

München

Stuttgart

Düsseldorf

Köln

Frankfurt

Mannheim

Bonn

Numberoftripsonedge

Figure 4: Usage of edges: occurance of jams, but not known by the vehicles.

search Center 637 “Autonomous Cooperating Logis-

tic Processes”.

REFERENCES

Becker, M., Wenning, B., G

org, C., Gehrke, J., Lorenz,

M., and Herzog, O. (2006). Agent-based and discrete

event simulation of autonomous logistic processes. In

Borutzky, W., Orsoni, A., and Zobel, R., editors, 20th

European Conference on Modelling and Simulation,

pages 566–571.

Bitran, G. and Tirupati, D. (1993). Hierarchical production

planning. In Graves, S., Kan, A. R., and Zipkin, P.,

editors, Logistics of Production and Inventory. North-

Holland.

Fiat, A. and Woeginger, G., editors (1998). Online Algo-

rithms. Springer.

Irani, S., Ku, X., and Regan, A. (2004). On-line algorithms

for the dynamic traveling repair problem. Journal of

Scheduling, 7:243–258.

Johnson, D. and Maltz, D. (1996). Dynamic source rout-

ing in ad hoc wireless networks. In Imielinski, T. and

Korth, H., editors, Mobile Computing. Kluwer.

ohler, E., M

ohring, R., and Schilling, H. (2005). Accel-

eration of shortest path and constrained shortest path

computation. In SE, N., editor, Proceedings of WEA

2005. Springer.

Langer, H., Timm, I., Sch

onberger, J., and Kopfer,

H. (2007). Integration von Software-Agenten

und Soft-Computing-Methoden f

ur die Transport-

planung. In Nissen, V. and Petsch, M., ed-

itors, Softwareagenten und Soft Computing im

Gesch

aftsprozeß-Management, pages 39–51. Cuvil-

lier.

Powell, W., Jaillet, P., and Odoni, A. (1995). Stochastic and

dynamic networks and routing. In Ball, M., Magnanti,

T., Monma, C., and Nemhauser, G., editors, Network

Routing. Elsevier.

Roughgarden, T. (2005). Selﬁsh Routing and the Price of

Anarchy. MIT Press.

Wenning, B., Pesch, D., and Timm-Giel, A. (2006). A dis-

tributed routing approach for vehicle routing in logis-

tic networks. In Proceedings of the 64th IEEE VTC.

Wenning, B., Rekersbrink, H., Becker, M., Timm-Giel, A.,

org, C., and Scholz-Reiter, B. (2007). Dynamic

transport reference scenarios. In H

ulsmann, M. and

Windt, K., editors, Understanding Autonomous Coop-

eration and Control in Logistics - The Impact on Man-

agement, Information and Communication and Mate-

rial Flow (to appear). Springer.

ICEIS 2007 - International Conference on Enterprise Information Systems

230