
PROBLEMS AND FEATURES OF EVOLUTIONARY ALGORITHMS
TO BUILD HYBRID TRAINING METHODS FOR RECURRENT
NEURAL NETWORKS
M. P. Cu
´
ellar, M. Delgado and M. C. Pegalajar
Dept. of Computer Science and Artificial Intelligence, University of Granada
C/. Pdta. Daniel Saucedo Aranda s.n., Granada, Spain
Keywords:
Recurrent Neural Network, hybrid algorithms, time series.
Abstract:
Dynamical recurrent neural networks are models suitable to solve problems where the input and output data
may have dependencies in time, like grammatical inference or time series prediction. However, traditional
training algorithms for these networks sometimes provide unsuitable results because of the vanishing gradient
problems. This work focuses on hybrid proposals of training algorithms for this type of neural networks. The
methods studied are based on the combination of heuristic procedures with gradient-based algorithms. In the
experimental section, we show the advantages and disadvantages that we may find when using these training
techniques in time series prediction problems, and provide a general discussion about the problems and cases
of different hybridations based on genetic evolutionary algorithms.
1 INTRODUCTION
Artificial neural networks (Haykin, 1999) are bio-
inspired mathematical tools that have been widely
used to solve complex engineering and real-world
problems involving classification, function approxi-
mation, learning, control tasks, etc. In general, the
use of a neural network may be recommended to solve
problems with non-linear behavior, high noise data,
lack of information in the data, and when the system
is complex and difficult to model.
Dynamical recurrent neural networks (DRNNs)
(Mandic and Chambers, 2001) may be obtained from
a classic feedforward network model by adding feed-
back connections to the network structure. This fea-
ture provides the network with long and short term
memory and makes it suitable to be used in problems
such as grammatical inference, time series prediction,
signal processing and, in general, problems where the
patterns to be learned have an undetermined size or
temporal properties. The classic learning methods
for DRNNs are based on gradient and error propaga-
tion, like in the feedforward models. However, these
methods may produce an unsuitable network training
due to vanishing gradient problems. Since this dis-
advantage is higher in recurrent neural networks, the
training may produce a poor network learning across
the recurrence (Bengio et al., 1994), particularly in
cases when the long-term network memory feature is
needed to solve the problem.
In the last decade, there have been many ap-
proaches for avoiding vanishing gradient problems
when training neural networks, and interesting re-
sults have been obtained. Most of these are based
on heuristic procedures such as the tabu search (La-
guna and Mart
´
ı, 2003), simulated annealing, particle
swarm, genetic algorithms, etc. (Blanco et al., 2001).
The main idea of these models is to make a global
search in the solution network space to avoid local
training. Their disadvantage, however, is the compu-
tational time needed to train the network if the prob-
lem to be solved is complex.
Other training procedures, on the other hand, use
the second derivative of the error regarding the net-
work weights (or its numerical approximation) to
solve the vanishing gradient problem. Some exam-
ples are Quasi-Newton optimization methods adapted
to neural network training, based on formulas such as
Levenberg-Marquardt or BFGS (Cu
´
ellar et al., 2005).
These methods may improve the network training ef-
ficiently; however, if the problem to be solved is com-
plex, the final network trained depends highly on the
204
P. Cuéllar M., Delgado M. and C. Pegalajar M. (2007).
PROBLEMS AND FEATURES OF EVOLUTIONARY ALGORITHMS TO BUILD HYBRID TRAINING METHODS FOR RECURRENT NEURAL
NETWORKS.
In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 204-211
DOI: 10.5220/0002383502040211
Copyright
c
SciTePress
initial network weights. These methods usually pro-
vide local solutions, thereby needing several experi-
ments to ensure a suitable training.
The combination of heuristic procedures with
gradient-based training algorithms has been put for-
ward by researchers to develop new hybrid methods
that combine the advantages of both techniques for
the improvement of network learning (Ku and Mak,
1997); (Prudencio and Ludermir, 2003); (Cu
´
ellar
et al., 2006). The main idea of hybrid train-
ing algorithms is to perform a global search us-
ing a heuristic procedure in order to locate the
best areas of the solution space. A gradient-based
method is then applied to improve the solution net-
work locally. These techniques are also known as
memetic algorithms (Moscato and Porras, 2003). Ad-
ditional information about hybrid algorithms (not
only related to neural network training but more
applications) can be found on the Memetic algo-
rithm web page at http://www.densis.fee.unicamp.br/
˜moscato/memetic
home.html.
In this paper, we combine evolutionary algorithms
with Quasi-Newton optimization procedures to train
DRNNs. More specifically, we study the features and
problems that we may find in an evolutionary method
to build a hybrid training algorithm, depending on the
strategy used to make the hybridization. The network
model is the dynamical Elman recurrent neural net-
work, since it has provided suitable results in the ex-
periments. The proposals are tested in time series pre-
diction problems.
Section 2 explains the DRNN model used in this
paper. Section 3 outlines the hybrid training models
considered. Section 4 then shows the experiments.
Finally, Section 5 presents the conclusions.
2 ELMAN RECURRENT
NETWORK MODEL
Dynamical recurrent neural networks (Mandic and
Chambers, 2001) are input/output mapping models
that may be obtained from a feedforward network by
adding recurrent connections to the network topol-
ogy. The best-known DRNN models are the fully con-
nected recurrent neural network, the Jordan network,
and the Elman network. In this article, we use the El-
man network (Elman, 1990) since it has obtained the
best results in a previous experimental study. It con-
tains three neuron layers: input data layer, hidden (or
processing) layer and output data layer. Since the re-
current connections are in the hidden layer, the output
value of a hidden neuron at time t is also the input for
all the hidden neurons at time t+1. This provides the
Elman network with long- and short-term memory in
time, codified in the network structure by means of
recurrent neurons.
.
.
.
.
.
.
X
1
(t)
X
n
(t)
V
S
1
(t)
S
2
(t)
S
h
(t)
O
1
(t)
U
.
.
.
O
o
(t)
W
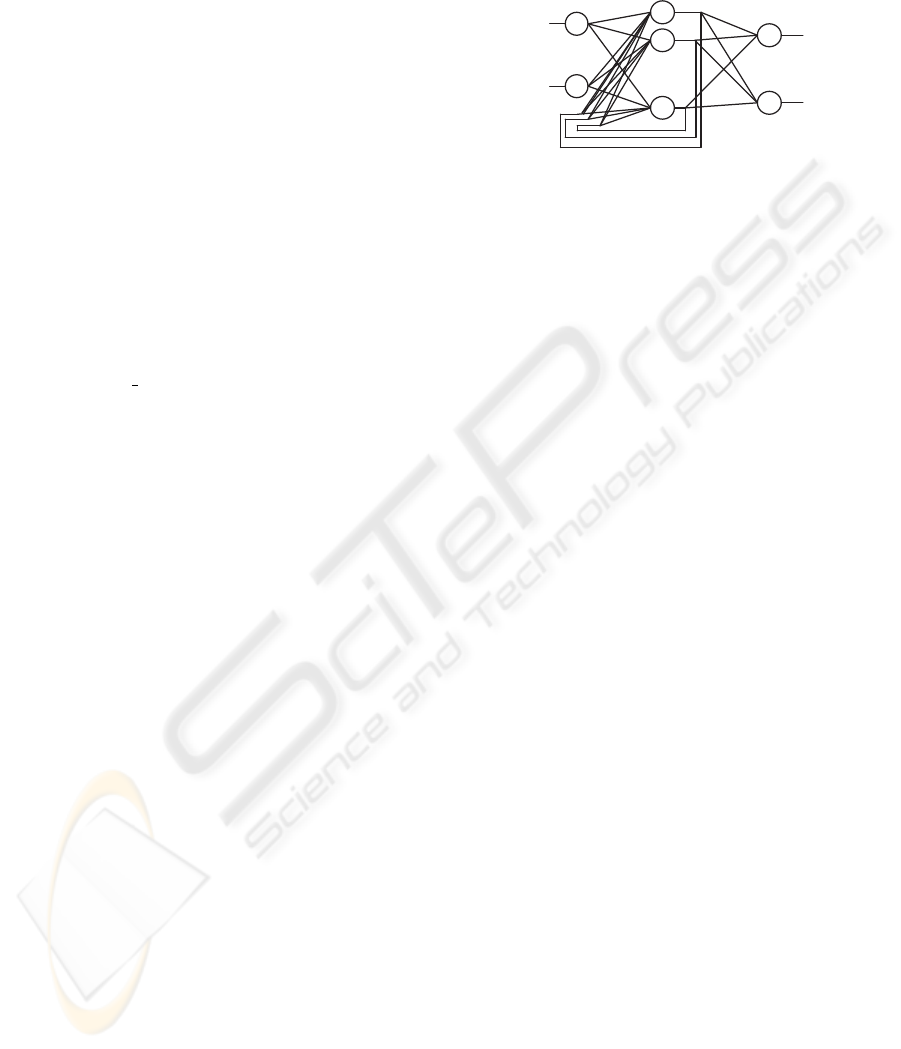
Figure 1: Example of an Elman network with n inputs, h
hidden neurons, and o outputs.
The diagram in Figure 1 illustrates an example of
an Elman recurrent neural network where:
• n, h, o are the number of input, hidden and output
neurons, respectively;
• X
i
(t) is the input data to neuron i at time t (1 <=
i <= n);
• S
j
(t) is the output of hidden neuron j at time t
(1 <= j <= h);
• O
k
(t) is the k-th network output at time t (1 <=
k <= o);
• the values U, V, W are matrices that encode the
network weights, so that V
ji
is the weight for the
connection from input neuron i to hidden neuron
j; U
jr
is the weight for the recurrent connection
from hidden neuron r to hidden neuron j; and
W
k j
is the weight for the connection from hidden
neuron j to output neuron k.
The equations for the network dynamics are:
S
j
(t) = f(
h
∑
r=1
U
jr
S
r
(t − 1) +
n
∑
i=1
V
ji
X
i
(t)) (1)
O
k
(t) = g(
h
∑
j=1
W
k j
S
h
(t − 1)) (2)
In Equations 1 and 2, f(x) is the sigmoid function
and g(x) is the identity function.
3 HYBRID TRAINING OF
RECURRENT NEURAL
NETWORKS
This section describes how to combine a genetic al-
gorithm with a gradient-based optimization algorithm
PROBLEMS AND FEATURES OF EVOLUTIONARY ALGORITHMS TO BUILD HYBRID TRAINING METHODS
FOR RECURRENT NEURAL NETWORKS
205

to train dynamical recurrent neural networks. Sub-
section 3.1 shows the codification of an Elman net-
work into a vector. Subsection 3.2 then explains
how to train an Elman network with a Quasi-Newton
procedure based on the BFGS formula. Subsection
3.3 outlines the method and strategies for combin-
ing both genetic and gradient-based algorithms to im-
prove DRNN training. Finally, Subsection 3.4 shows
the hybridizations considered in this work.
3.1 Codification of the Elman Network
Let us assume that the number of network inputs n,
hidden units h, and network outputs o is known. Us-
ing the notation from Section 2, the number of net-
work weights Q is computed as shown in Equation 3.
Q = h(n+ h+ o) (3)
An Elman network is codified into a Q-
dimensional vector. A component in the vector is as-
signed to a network connection, and the value of that
component is the weight for the corresponding net-
work connection. Figure 2 shows an example of the
codification of an Elman network with 1 inputs, 2 hid-
den units and 1 output into a vector.
V
11
V
21
U
11
U
12
U
21
U
22
W
11
W
12
Figure 2: Example of a vector encoding an Elman network
with 1 inputs, 2 hidden neurons, and 1 outputs.
3.2 Training an Elman Network with
the BFGS Algorithm
The BFGS algorithm is a non-linear programming
method that optimizes a solution iteratively. At each
iteration k, the solution S
k
is modified according to a
search direction d
k
and a step length α
k
. The search
direction d
k
is computed using an approximation of
the second derivative of the error in the network out-
puts with regard to the network weights. Equations
4-7 illustrate this idea.
S
k+1
= s
k
+ d
k
α
k
(4)
d
k
= H
k
G
k
(5)
H
k+1
= H
k
+
(S
k+1
− S
k
)(S
k+1
− S
k
)
t
(S
k+1
− S
k
)
t
(G
k+1
− G
k
)
−
H
k
(G
k+1
− G
k
)(G
k+1
− G
k
)
t
H
k
(G
k+1
− G
k
)
t
H
k
(G
k+1
− G
k
)
(6)
G
k
= (
∂
∂V
11
f(S
k
), ...,
∂
∂V
hn
f(S
k
),
∂
∂U
11
f(S
k
), ...,
∂
∂U
hh
f(S
k
),
∂
∂W
11
f(S
k
), ...,
∂
∂W
oh
f(S
k
)) (7)
The value α
k
, however, is computed by minimiz-
ing the objective function for an approximation of the
solution at the next iteration (Equation 8).
α
k
= argmin
α>0
{ f(S
k
+ α
k−1
d
k
)} (8)
An in-depth explanation of the BFGS algorithm
and its adaptation for training DRNNs can be found in
(Byrd et al., 1995); (Cu
´
ellar et al., 2005); (Zhu et al.,
1997).
3.3 Hybridization Strategies
A hybrid training algorithm for neural networks may
be obtained by combining a heuristic procedure with
a gradient-based optimization method. If the hy-
bridization combines an evolutionary algorithm with
the gradient-based method as a local search opera-
tor, then it is called a memetic hybridization. Vari-
ous authors have published suggestions and experi-
mental tests for building a memetic or hybrid algo-
rithm to solve different problems. Further information
about this issue may be found in (Moscato and Porras,
2003). The main strategies suggested for making hy-
bridizations are:
• The Lamarckian hybridization: the performance
of a solution in the evolutionary algorithm is im-
proved by means of local learning before evalu-
ation. After improvement, the initial solution is
modified with the improved solution, and also its
fitness value.
• The Baldwinian hybridization: as in the Lamarck-
ian hybridization, the performance of a solution in
the evolutionary process is improved with a local
search operator before its evaluation. The fitness
value of the initial solution is then modified with
the fitness of the improved solution. However, the
initial solution itself is not altered after improve-
ment.
In this paper, we will test both strategies in differ-
ent evolutionary schemata, combined with the BFGS
algorithm as a local search operator. In the experi-
mental section, we will test the proposals in order to
discover the effects of each one in the problems stud-
ied.
3.4 Hybrid Proposals
This subsection describes the main schemata of the
evolutionary algorithms to be hybridized with the
ICEIS 2007 - International Conference on Enterprise Information Systems
206

BFGS algorithm. We have considered the classic ge-
netic generational, stationary and mixed evolution-
ary schemata in addition to the CHC evolution strat-
egy, since these algorithms are suitable for illustrat-
ing the main features and problems of the hybridiza-
tions in the experimental section. Firstly, Subsection
3.4.1 explains the construction of the hybrid genetic
algorithms. Subsection 3.4.2 then presents the hybrid
CHC algorithm.
3.4.1 Hybrid Genetic Algorithms
The hybrid genetic procedures may be obtained from
classic genetic schemata by applying a local search
method to the solutions in the population before they
are evaluated. The following algorithm shows the
main idea for making this hybridization:
procedure HGA(Input: l, L, C, N, F; Output: S)
- l: lower bound for the network weights
- L: upper bound for the network weights
- C: stopping criterion
- N: size of the population
- F(s): objective function (supposed to be
minimized). ’s’ is a vector encoding
a solution network
- S: solution network
Begin
1. set P= Generate N random solutions
with the weights in [l, L]
2. Evaluate solutions in P
3. While (C is not satisfied) do
4. begin
5. set P’= selection of solutions in P
6. set H= combination of solutions in P’
7. set H’= mutation of solutions in H
8. For each solution h in H’ do
9. begin
10. set h’= improvement of h
11. if (F(h’) < F(h)) then
12. begin
13. set Fitness(h)= Fitness(h’)
14. if (Lamarckian hybridation is
15. applied) then set h= h’
16. end
17. end.
18. Replacement of solutions in P with H’
19. Elitism in P, if required
20. end.
21. set S= best solution in P
22. Return S
End.
The previous schema may be used for the gener-
ational, stationary or mixed genetic models with the
following characteristics:
• In the generational model, Step 5 makes N selec-
tions in P to build the set of solutions to be com-
bined, where N is the size of the population. Step
6 also generates N new solutions, and Step 18 re-
places P with the N solutions in H’
• In the stationary model, Step 5 makes K selec-
tions in P, where K is a parameter to the algorithm,
to generate K new solutions in Step 6. In this case,
the replacement strategy in Step 18 may be to re-
place the worst solutions in the population, to re-
place the parents, etc.
• The mixed model is equivalent to the stationary
one at Steps 5 and 6. However, all the solutions
in P and H’ are mutated in Step 7. Therefore, the
replacement strategy in Step 18 is equivalent to
the one in the generational model.
In the experimental section, we will use
GGA/BFGS to denoted hybridization with the gen-
erational genetic schema, SGA/BFGS for hybridiza-
tion with the stationary one, and MGA/BFGS for hy-
bridization with the mixed strategy.
3.4.2 Hybrid CHC Algorithm
The CHC algorithm is one of the first proposals in
evolutionary algorithms that include a balance in the
method to control the diversity and convergence in the
population. In this paper, the hybrid CHC algorithm
may be obtained with the CHC evolutionary proce-
dure (which is adapted to solve real-coded solutions)
by applying a local search method to the solutions in
the population before they are evaluated. The follow-
ing algorithm shows the hybrid method:
procedure HCHC(Input: l, L, C, N, U, M, F;
Output: S)
- l: lower bound for the network weights
- L: upper bound for the network weights
- C: stopping criterion
- N: size of the population
- U: parameter to compute the threshold
combination
- M: number of solutions in the population
to be combined (M must be odd)
- F(s): objective function (supposed to be
minimized). ’s’ is a vector encoding
a solution network
- S: solution network
Begin
1. set P= Generate N random solutions
with the weights in [l, L]
2. Evaluate solutions in P
3. Compute D= Average Euclidean distance
of solutions in P
4. Compute d= U*D
3. While (C is not satisfied) do
4. begin
5. set P’= selection of M solutions in P
6. set H= empty set
PROBLEMS AND FEATURES OF EVOLUTIONARY ALGORITHMS TO BUILD HYBRID TRAINING METHODS
FOR RECURRENT NEURAL NETWORKS
207

7. For i=1 to M (increment i=i+2) do
8. begin
9. E= Euclidean distance in H(i)
and H(i+1)
10. if (E>D) then
11. begin
12. set h1, h2= combine solutions H(i)
and H(i+1)
13. set H=H+{h1,h2}
14. end.
15. end.
16. if (size of H is zero) then
17. set D= D-d
18. if (D<=0) then
19. begin
20. set S= best solution in P
21. set P= Generate N random solutions
+{S}
22. Evaluation of new solutions in P
23. Compute D= Average Euclidean distance
of solutions in P
24. Compute d= U*D
25. end.
26. For each solution h in H do
27. begin
28. set h’= improvement of h
29. if (F(h’) < F(h)) then
30. begin
31. set Fitness(h)= Fitness(h’)
32. if (Lamarckian hybridation is
33. applied) then set h= h’
34. end
35. end.
36. set P= N best solutions in P and H
37. end.
38. set S= best solution in P
39. Return S
End.
The main features of the CHC for controlling the
diversity and convergence in the population are:
• The use of a combination procedure that gener-
ates new solutions which are as different from the
parents as possible in order to explore the space
solution. In this paper, we use the BLX − α re-
combination operator for real-coded genetic algo-
rithms.
• The incest prevention (lines 9-10) to avoid similar
solutions to be combined.
• The re-initialization of the population (lines 18-
25) if the search has converged to an area in the
solution space.
• An elitist selection (line 38) to ensure conver-
gence.
In the experimental section, we will study how the
hybridization strategies may alter these properties in
a hybrid algorithm. We note the hybrid algorithm as
CHC/BFGS.
4 EXPERIMENTS
4.1 Data Sets and Parameters
The methods developed in this paper have been tested
on the following time series prediction problem:
• The CATS time series benchmark (Lendasse et al.,
2004). This data set was proposed in 2004 at the
IJCNN congress. It is subdivided into five data
sets, each containing 980 data. The next 20 val-
ues must be predicted. We denote these sets from
CATS1 to CATS5.
In all the data sets, we use the first 80% of data for
training and test with the remaining 20% of values.
The parameters for the Elman network are:
• Input neurons: 1, corresponding to value Y(t) of
the time series.
• Output neurons: 1, corresponding to value Y(t +
1) to be predicted.
• Hidden neurons: 9.
• Bounds for the network weights: in the range [-
10.0, 10.0]
For the prediction, the network output at time t
(which is an approximation of Y(t + 1)) is used as a
network input at time t + 1. This procedure is looped
K times until we obtain the value Y(t + K) to be pre-
dicted.
The parameters for the hybrid genetic algorithms
are:
• Size of the parents set K: 2 (only for the stationary
and the mixed strategies)
• Mutation operator: displacement
• Probability for combination: 0.8 for the
GGA/BFGS, 1.0 for the other proposals.
• Probability for mutation: 0.1
• Replacement method (for SGA/BFGS): the off-
spring replace the parents in the population
• Elitism: the 2 best solutions remain in the popula-
tion.
The parameters for the hybrid CHC/BFGS algo-
rithm are:
• Number of parents to be combined M: 50
• Threshold decreasing rate U: 0.1
The parameters that are common for all the evolu-
tionary hybrid methods are:
• Stopping criterion: 2000 solutions are evaluated
• Size of the population: 50
ICEIS 2007 - International Conference on Enterprise Information Systems
208

• Local search operator: BFGS. This is iterated 20
times in each solution.
• Hybridization strategy: Lamarckian/Baldwinian
• Selection of parents: binary tournament selection
• Combination operator: BLX − α, α = 0.5
All the algorithms have been run 30 times. The al-
gorithms of the above are compared using the number
of solutions evaluated. We have also included other
algorithms to test the methods:-
• A multi-start BFGS training procedure: this
method is compared with the hybrids in terms of
computing time. The stopping criterion for this al-
gorithm is to reach the average time of the hybrid
algorithm that provided the best results.
• A metaheuristic scatter search method(Laguna
and Mart
´
ı, 2003): this algorithm is compared in
terms of the solutions evaluated.
• A classic genetic algorithm with a stationary strat-
egy: this algorithm is compared with the hybrids
in terms of the solutions evaluated.
4.2 Experimental Results
Table 1 shows the average mean square error (MSE)
for the hybrid algorithms in the test sets. Column 1
shows the algorithm, and Columns 2-6 show the av-
erage MSE in each data set. A Kolmogorov-Smirnoff
test with 0.1 confidence level has been applied to the
results in order to check normality in the data distri-
bution. In Table 1, we use (+) to denote whether the
data has passed the test, and (-) otherwise.
The results in Table 1 show that, on average, the
hybrid algorithm of a genetic procedure with station-
ary strategy and the BFGS method (SGA/BFGS) per-
forms suitably in most problems, particularly when
we use the Baldwinian strategy.
In general, we can observe how the Baldwinian
strategy performs better than the Lamarckian one.
However, another interesting issue is the results
obtained with CHC/BFGS hybridization with the
Lamarckian strategy, which are much worse than
the respective CHC/BFGS with the Baldwinian hy-
bridization. The main difference between applying a
Baldwinian or a Lamarckian hybridization is that the
diversity in the population may be altered using this
last method. In this last case, the genes in the ini-
tial solution are in fact replaced by the genes in the
improved one, and the balance between diversity and
convergence in the CHC algorithm is therefore bro-
ken, thereby providing unsuitable results.
We have performed a non-parametric statistical
Kruskal-Wallis test with a 0.05 confidence level to
support our assumptions. Tables 2-3 show these re-
sults and the columns present the test for the data
sets. Each column is organized in the following way:
the algorithms are ordered in increasing order of the
median of the distribution data. The value in brack-
ets shows the result of the statistical test of an algo-
rithm compared with the best of the previous equiva-
lent ones. If the results are statistically relevant (i.e.
the algorithm is worse than the previous one), then the
algorithm is marked (-). Otherwise, if the results are
not statistically relevant (i.e. the results of the com-
pared methods are statistically equivalent), then the
algorithm is marked (x).
Tables 2 and 3 show that the best results are ob-
tained with the SGA/BFGS hybridization in most
cases, and also that the selection of the hybridiza-
tion strategy is not a key aspect in this hybrid method.
If we compare the genetic hybridizations separately,
certain conclusions may be drawn for the data stud-
ied:
• The hybridizations with the generational and
mixed strategies generally provide worse results
than the stationary one. This may be due to the
effects of the elitist selection and recombination
in this last proposal. For example, at each iter-
ation, the SGA/BFGS algorithm selects two par-
ents to generate two new solutions. However, in
the GGA/BFGS and MGA/BFGS algorithms, at
each iteration N solutions are evaluated, where N
is the size of the population. The effect of this
situation is that the GGA/BFGS and MGA/BFGS
methods are more similar to a multi-start proce-
dure than SGA/BFGS.
• In fact, the results of the GGA/BFGS and
MGA/BFGS methods are usually statistically
equivalent or even worse than the multi-start
BFGS procedure. The reason for this is that
the hybrid genetic algorithms are run for 2000
evaluations, with a population of N= 50 solu-
tions, and a local search improvement of 20 iter-
ations/solution. In the first iteration, a total num-
ber of 50*20= 1000 iterations are therefore car-
ried out. The same occurs for the second itera-
tion, where the stopping criterion is when 2000
solutions have been evaluated. In these cases, the
genetic procedures cannot perform well since the
genetic operators are not allowed to take effect
over the population. Thus, in the best of cases,
the results of these algorithms will be statistically
equivalent to a multi-start BFGS procedure. On
the other hand, we may expect the results to be
worse in the GGA/BFGS and MGA/BFGS hy-
bridizations since the last 1000 iterations are car-
ried out over similar solutions to the first 1000 it-
PROBLEMS AND FEATURES OF EVOLUTIONARY ALGORITHMS TO BUILD HYBRID TRAINING METHODS
FOR RECURRENT NEURAL NETWORKS
209

erations (since the population at the second ge-
netic iteration is obtained from the population in
the first iteration).
• In terms of comparison with the scatter search
metaheuristic procedure, suitable results are ob-
tained and in most cases, these are statistically
equivalent to the results of the SGA/BFGS meth-
ods.
• Another interesting aspect is the effect of the hy-
bridization strategy on SGA/BFGS methods. In
most cases, there is no statistical relevance in ap-
plying both techniques in this hybridization. By
way of partial conclusion, we may expect the eli-
tist factor of the SGA/BFGS algorithm to be more
important for making this hybridization than the
hybridization strategy itself.
• All the methods that include the BFGS procedure
perform better than a stationary genetic algorithm.
Therefore, the main conclusion that we may ob-
tain from this fact is that it is preferable to use a
Quasi-Newton method if it is possible to compute
the gradient, instead of using a heuristic procedure
such as SGA.
5 CONCLUSIONS
This work has presented various aspects of using hy-
brid training algorithms for recurrent neural networks.
We have studied the behavior of certain hybrid meth-
ods proposed experimentally in a concrete time se-
ries prediction problem: the CATS benchmark. Our
conclusion is that a Baldwinian hybridization strategy
is generally preferable since it does not alter popu-
lation diversity (this is exemplified by the results of
the CHC/BFGS method). In certain cases, however,
such as in a stationary genetic hybridization, the eli-
tist properties of the model are more important than
the hybridization strategy itself. It is also important
to consider the effects of the improvement method
against those from genetic operators since excessive
use of the local search operator may negatively af-
fect the genetic selection, recombination and muta-
tion processes (this is the case of MGA/BFGS and
GGA/BFGS).
In general, the results suggest that a hybrid
method may improve the performance in the training
of a recurrent neural network for time series predic-
tion problems. However, abuse of the local search
operator may produce statistical equivalence in the
results against the multi-start procedure. In order to
avoid this, special attention should be paid to the de-
sign of the optimization of the hybrid algorithm pa-
rameters.
REFERENCES
Bengio, Y., Simard, P., and Frasconi, P. (1994). Learning
long-term dependencies with gradient descent is diffi-
cult. IEEE Trans. on Neural Networks, 5(2):157–166.
Blanco, A., Delgado, M., and Pegalajar, M. C. (2001).
A real-coded genetic algorithm for training recurrent
neural networks. Neural Networks, 14:93–105.
Byrd, R., Lu, P., and Nocedal, J. (1995). A limited
memory algorithm for bound constrained optimize-
tion. SIAM Journal on Scientific and Statistical Com-
puting, 16(5):1190–1208.
Cu
´
ellar, M., Delgado, M., and Pegalajar, M. (2005). An ap-
plication of non-linear programming to train recurrent
neural networks in time series prediction problems. In
Proc. of International Conference on Enterprise and
Information Systems (ICEIS’05), pages 35–42, Miami
(USA).
Cu
´
ellar, M., Delgado, M., and Pegalajar, M. (2006).
Memetic evolutionary training for recurrent neural
networks: an application to time-series prediction. Ex-
pert Systems, 23(2):99–117.
Elman, J. (1990). Finding structure in time. Cognitive Sci-
ence, 14:179–211.
Haykin, S. (1999). Neural Networks: A Comprehensive
Foundation. Prentice Hall.
Ku, K. and Mak, M. (1997). Exploring the effects of lamar-
ckian and baldwinian learning in evolving recurrent
neural networks. In Proc. of the IEEE International
Conference on Evolutionary Computation.
Laguna, M. and Mart
´
ı, R. (2003). Scatter Search. Method-
ology and Implementations in C. Kluwer Academic
Publishers.
Lendasse, A., Oja, E., Simula, O., and Verleysen, M.
(2004). Time series competition: The cats bench-
mark. In Proc. International Joint Conference on
Neural Networks (IJCNN’04), pages 1615–1620, Bu-
dapest (Hungary).
Mandic, D. and Chambers, J. (2001). Recurrent Neural Net-
works for Prediction. John Wiley and sons.
Moscato, P. and Porras, C. C. (2003). An introduction to
memetic algorithms. Inteligencia Artificial (Special
Issue on Metaheuristics), 2(19):131–148.
Prudencio, R. and Ludermir, T. (2003). Neural network
hybrid learning: Genetic algorithms and levenberg-
marquardt. In Proc. 26th Annual Conference of the
Gesellschaft fr Classifikation, pages 464–472.
Zhu, C., Byrd, R., and Nocedal, J. (1997). L-bfgs-b. algo-
ritmo 778: L-bfgs-b, fortran routines for large scale
bound constrained optimization. ACM Transactions
on Mathematical Software, 23(4):550–560.
ICEIS 2007 - International Conference on Enterprise Information Systems
210
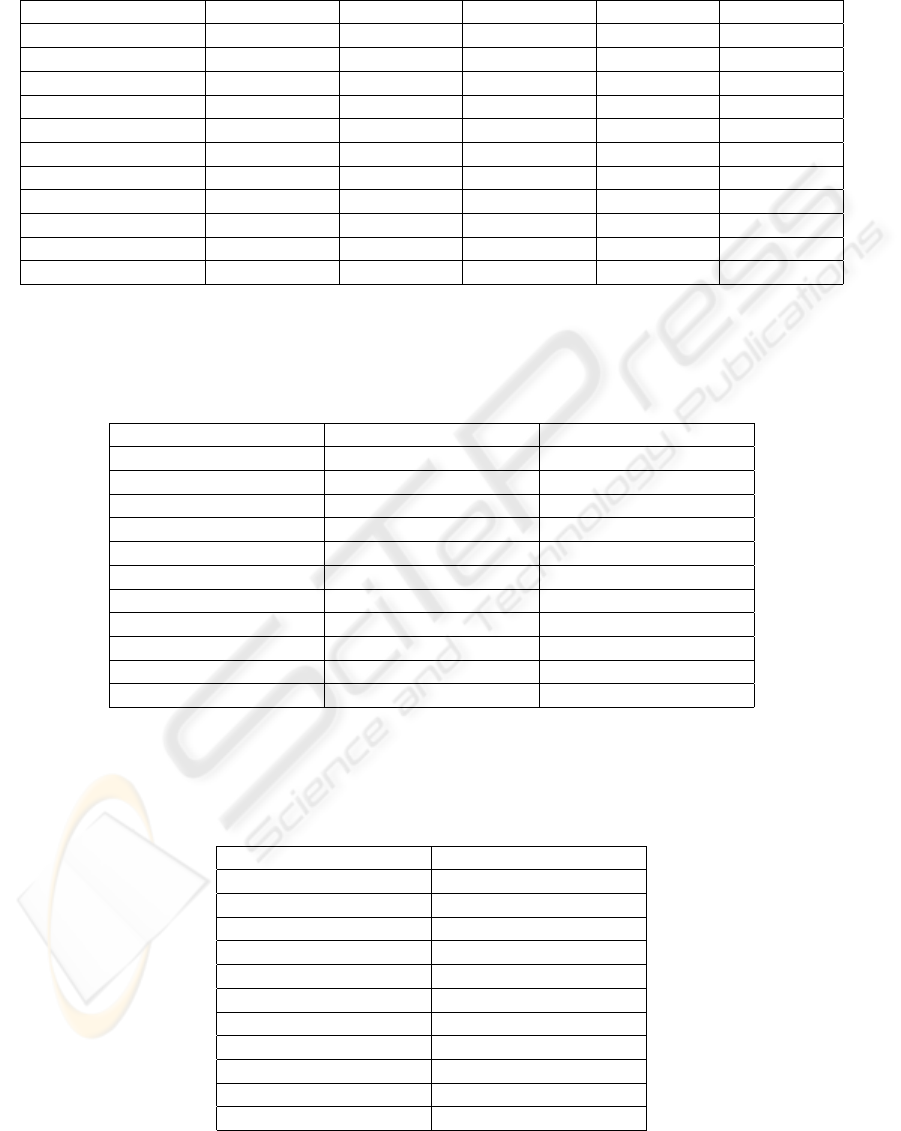
Table 1: MSE for the hybrid algorithms in the test sets.
Algorithm CATS1 CATS2 CATS3 CATS4 CATS5
GGA/BFGS (Lam.) 172.10 (-) 161.21 (-) 153.06 (-) 146.87 (-) 222.11 (-)
GGA/BFGS (Bal.) 168.69 (-) 167.56 (-) 155.56 (-) 145.85 (+) 210.07 (-)
SGA/BFGS (Lam.) 163.14 (-) 156.33 (-) 142.16 (+) 140.05 (-) 216.39 (-)
SGA/BFGS (Bal.) 159.78 (+) 155.16 (-) 141.80 (+) 137.02 (-) 214.10 (-)
MGA/BFGS (Lam.) 165.07 (-) 163.63 (-) 167.12 (-) 161.87 (-) 206.79 (-)
MGA/BFGS (Bal.) 167.81 (-) 165.12 (-) 165.33 (-) 165.44 (-) 204.34 (-)
CHC/BFGS (Lam.) 135497.00 (-) 87281.55 (-) 107627.70 (-) 47834.53 (-) 67331.09 (-)
CHC/BFGS (Bal.) 160.17 (-) 159.09 (+) 149.51 (-) 143.41 (+) 220.15 (-)
Scatter Search 161.93 (+) 158.84 (-) 156.48 (+) 141.60 (+) 276.44 (-)
BFGS 165.12 (-) 164.89 (-) 150.18 (-) 143.81 (+) 208.89 (-)
SGA 222.71 (-) 617.96 (-) 337.84 (-) 318.47 (-) 455.09 (-)
Table 2: Kruskal-Wallis test for the hybrid algorithms in the test sets.
CATS1 CATS2 CATS3
SGA/BFGS (Bal.) (x) SGA/BFGS (Bal.) (x) SGA/BFGS (Bal.) (x)
SGA/BFGS (Lam.) (x) SGA/BFGS (Lam.) (x) SGA/BFGS (Lam.) (x)
Scatter Search (x) CHC/BFGS (Bal.) (x) CHC/BFGS (Bal.) (x)
CHC/BFGS (Bal.) (x) Scatter Search (x) BFGS (-)
BFGS (x) GGA/BFGS (Lam.) (-) GGA/BFGS (Lam.) (-)
MGA/BFGS (Bal.) (-) GGA/BFGS (Bal.) (x) GGA/BFGS (Bal.) (x)
MGA/BFGS (Lam.) (x) MGA/BFGS (Lam.) (x) Scatter Search (x)
GGA/BFGS (Bal.) (x) MGA/BFGS (Bal.) (-) MGA/BFGS (Lam.) (x)
GGA/BFGS (Lam.) (-) BFGS (x) MGA/BFGS (Bal.) (-)
SGA (-) SGA (-) SGA (-)
CHC/BFGS (Lam.) (-) CHC/BFGS (Lam.) (-) CHC/BFGS (Lam.) (-)
Table 3: Kruskal-Wallis test for the hybrid algorithms in the test sets.
CATS4 CATS5
SGA/BFGS (Bal.) (x) MGA/BFGS (Bal.) (x)
SGA/BFGS (Lam.) (-) MGA/BFGS (Lam.) (x)
BFGS (x) GGA/BFGS (Bal.) (x)
CHC/BFGS (Bal.) (x) BFGS (x)
Scatter Search (x) SGA/BFGS (Bal.) (x)
GGA/BFGS (Bal.) (x) SGA/BFGS (Lam.) (x)
GGA/BFGS (Lam.) (-) CHC/BFGS (Bal.) (x)
MGA/BFGS (Lam.) (x) GGA/BFGS (Lam.) (-)
MGA/BFGS (Bal.) (-) Scatter Search (x)
SGA (-) SGA (-)
CHC/BFGS (Lam.) (-) CHC/BFGS (Lam.) (-)
PROBLEMS AND FEATURES OF EVOLUTIONARY ALGORITHMS TO BUILD HYBRID TRAINING METHODS
FOR RECURRENT NEURAL NETWORKS
211
