EMPLOYING SOFTWARE MULTI-AGENTS FOR SIMULATING

RADIOLOGICAL ACCIDENTS

Tadeu Augusto de Almeida Silva and Oscar Luiz Monteiro de Farias

Universidade do Estado do Rio de Janeiro & Instituto de Radioproteção e Dosimetria (IRD)

Programa de Pós-Graduação em Engenharia de Computação

Rua S.Francisco Xavier, 524, sala 5017, CEP 20550-900, Maracanã, Rio de Janeiro, RJ, Brasil

Keywords: Agents, Radiological Accident, GIS.

Abstract: Through agent based systems we can build scenarios of radiological accidents that enable us to evaluate the

consequences of accidental contaminations. The incidental release of radionuclides in an environment might

cause the contamination of areas and people. So, it is necessary to make use of tools that allow us to foretell

the effects of the exposition of the population and to evaluate the consequences and to suggest measures of

protection. In this paper we introduce the use of software multi-agents systems immersed in a geographical

representation of the world, as a viable option to simulate radiological accidents and assess doses.

1 INTRODUCTION

Radiological accidents can result in significant

radiation exposures of workers and of the public.

These accidents usually occur as a consequence

of human activities in military, industry, medicine,

agriculture and research, involving the use of

radiation and radioactive substances that cause

radiation exposure in addition to the natural

exposure. Study the impact of radiological accident

in society and learn the lessons for the future it is a

way to prevent further accidents.

So, planning immediate answers and actions to

emergency situations is a critical factor to establish

security policies. Simulation models incorporating

software agents are one of the tools that can be

successfully employed in these tasks. They can

mimic the “real world”, and the interaction among

people, materials and radioactive sources. Through

computational simulation of agent-based models,

people can perceive, with details, the effect of

radioactive contamination in case of accidents, what

makes easy the understanding of the risks involved

and the damages caused in such situations.

In this article we’ll show how to create an

environment where software agents simulate

radiological accidents. Our agents will have some

properties, as: mobility, reactivity and objectivity.

People and radioactive sources and elements will be

also represented by software agents, In this way,

through agent-based simulation, we intend to study,

analyse and manage these complex systems

(radiological accidents).

Here we use the following definition, of agent

(Franklin, Graesser, 1997): “A system situated within a

given environment, that senses that environment

through its perception mechanism and acts on that

environment and/or on other agents, as time flows,

in pursuit of its own agenda, plans or beliefs.

Eventually the agent´s perception/action mechanism

evolves with time”.

In this study it is necessary that multi-agent

systems can provide a computational platform where

the dynamic of spatio-temporal systems can be

analysed and the agents can interact ones with others

through communication mechanisms (Wooldridge,

2002) .

2 RADIOLOGICAL ACCIDENTS

Radiological accidents are accidents that occur in

nuclear or radioactive installations and are

characterized by the existence of intense fields of

not intentional radiation, not controlled release in the

environment of amounts of radioactive material, and

involve exposition or contamination of human

beings or the environment, being able to cause

serious damages or death.

436

Augusto de Almeida Silva T. and Luiz Monteiro de Farias O. (2007).

EMPLOYING SOFTWARE MULTI-AGENTS FOR SIMULATING RADIOLOGICAL ACCIDENTS.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 436-439

DOI: 10.5220/0002385904360439

 SciTePress

The incidental release of radionuclides in the

environment might cause the contamination of areas

and people. So, it is necessary to make use of tools

that allow us to foretell the effects of the exposition

of the population and to evaluate the consequences

and to suggest measures of protection (IAEA, 1996).

First of all, we need to identify the amount of

contaminated people, degree or dose of radiation

received and a more elaborate map (georeferenced

information) from the areas impacted (Agape, 2005).

A radiological accident can affect the public

transportation system, generate zones of exclusion

in the contaminated areas, leading to the

displacement of people, damage the water supply,

and overcrowd hospital services, causing serious

social problems (Agape, 2005).

For the evaluation of the dose received for

individuals it is necessary to take in consideration

the release rate of the radioactive source, its exact

distance from the exposed individuals, the existence

of materials (shield) between the radioactive source

and the exposed individuals, and the time of

exposition of the individuals. Through the

following formulas we can determine the dose:

A=A

λ.t

(1)

Where: A is the activity of a radioactive source, A

is the activity at time t=0, and λ

is the constant of

disintegration, meaning the rate in which

disintegration proceeds.

X = Γ.A / d

(2)

Where,

X = exposition rate, in R/h ( Roentgen / hour)

A = source activity, in Ci ( Curie )

d = distance between the source and the point of

measure, in meters.

 = a characteristic constant of each radioactive

source, also known as factor gamma, in (R.m

) /

(h.Ci)

over which

D = X.t

(3)

Where,

D = absorbed dose, in Gray (Gy)

X = exposition rate, in R/h

t = time, in hours (h)

DE = D.FQ

(4)

Where,

DE = dose equivalent , in Sievert (Sv)

D = absorbed dose, in Gray (Gy)

FQ = quality factor of radiation, for gamma

radiation FQ equals 1

3 ARCHITECTURE OF

AGENT-BASED SYSTEMS TO

SIMULATE RADIOLOGICAL

ACCIDENTS

The goal of our agent-based system is to furnish

useful information related to a given radiological

accident. This class of information is usually related

to: i) the quantity of persons that were esposed; ii)

the effective dose they received; iii) determination,

localization and extension of contaminated areas.

Not always it is possible to determine who

where the persons exposed, neither their exact

number. This would be the case, for example, of a

terrorist attack with a radioactive source in the

public system of transportation, for example in a

train or in a subway. Notwithstanding it is very

important for the public health system, to have a

estimate of the people involved and of the effective

dose they received, in order to calculate the medical

resources that will be need to face the problem, to

warn the population against the risks of exposure,

and also to manage the entire situation, all the risks

involved, descontamination procedures, etc.

Our model is based on the formula of radioactive

dispersion in the air (equation 2), leading in account

the radionuclide and its activity, the distance of the

people exposed to the radioactive element, the time

of exposition, as well as possible shields. We also

consider eventual movements of persons and of

radioactive sources. Both of them are represented by

very simple agents, People agents suffer the effects

of radioactive source agents, based on equation 2,

and these effects are registered on the state variables

of people agents. Shield effects could, as well, be

incorporated into the model.

The source agent has the following state

variables: i) The source Id; ii) Its position, given by

a tuple of coordinates (x, y, z); iii) Its activity A;

iv) The factor Γ for the specific source; v) The

quality factor (FQ), a factor used to weight the

absorbed dose with regard to its presumed biological

effectiveness. A typical agent, representative of a

person, has the following state variables: i) Person

Id; ii) Its position, given by a tuple of coordinates (x,

y, z); iii) Time of exposition; iv) Shield effect; v)

The absorbed dose; vi) The effective dose.

In our model we need also a representation for

the space, the environment from where our agents

take sensory inputs and produce as output actions,

that is, their movements. Normally Geographical

Information Systems (GIS) use raster or vector

structures to represent space in bi-dimensional

EMPLOYING SOFTWARE MULTI-AGENTS FOR SIMULATING RADIOLOGICAL ACCIDENTS

437

models. In some cases a third dimension is

represented through digital elevation models (dem)

of a terrain. Given a GIS spatial representation (a

shape file, for example), we’ll add to it software

agents and the structure of a dynamic spatial model,

in order to simulate the dynamic of radiological

accidents. The GIS spatial representation is the

environment or locus, where agents of our Agent-

Based Models will operate.

For each specific phenomenon, we are interested,

only, in particular information about the

environment. So, considering the geographical space

where the phenomenon develops, we need to filter

only the aspects of the environment we are

interested in, that is, the features that will compose

the environment as seen by the agents, and where all

the process will be simulated. This is not a difficult

task, for data is organized on GIS in different layers,

such that: utilities, river and lakes, roads and rails,

soil maps, land parcels, etc. We need to select only

the layers we are interested in. Objects that are not

of interest must be discharged, for an environment

full of superfluous objects would unnecessary

complicate the implementation and reduce the

simulation performance. So, depending on the

problem, we can simplify considerably the

simulation, as we´ll see below in our case study

(

Farias, Leite, 2005).

4 CASE STUDY: THE

RADIOLOGICAL ACCIDENT

AT COCHABAMBA, BOLÍVIA

We will take as our case study the radiological

accident occurred in Cochabamba, Bolivia, in 2002.

This accident was minutely documented and

physicaly reconstructed by the IAEA (IAEA, 2004),

and the assessment of doses estimated. So, we have

a valuable data to compare with the results of our

agent-based simulation and to validate our model.

In April 2002 an accident involving an industrial

radiography source containing

192

Ir occurred in

Cochabamba, Bolivia, some 400 km from the

capital, La Paz. The source, in a remote exposure

container, remained exposed within a guide tube,

although this was not known at the time. The

container, the guide tube and other equipment were

returned from Cochabamba to the headquarters of

the company concerned in La Paz as cargo on a

passenger bus. This bus carried a full load of

passengers for the journey of about eight hours from

Cochabamba to La Paz. The equipment was

subsequently collected by company employees and

transferred by taxi to their shielded facility. Routine

radiation measurements made there established that

the source was still exposed and actions were then

taken to return the source to its shielded container

(IAEA, 2004).

In our case study, due to the source

characteristics, the effect of the radiation was

relevant only to people situated a few meters from

the source, that is, for people inside the bus. If we

look at the exposition rate, absorbed dose and dose

equivalent (effective dose) formulas, we’ll see that

all these measures - given a specific source - are

dependent only of the relative position between the

source and the people exposed and of the time of

exposition. So, in this very special case, it doesn’t

matter the path followed by the source in its journey

from Cochabamba to La Paz. Assuming that all

passengers, after entering the bus, didn’t change

their seats, what is relevant to assess doses is: i) the

distance between each passenger and the radioactive

source that remained fix during the entire journey;

ii) the exposure time.

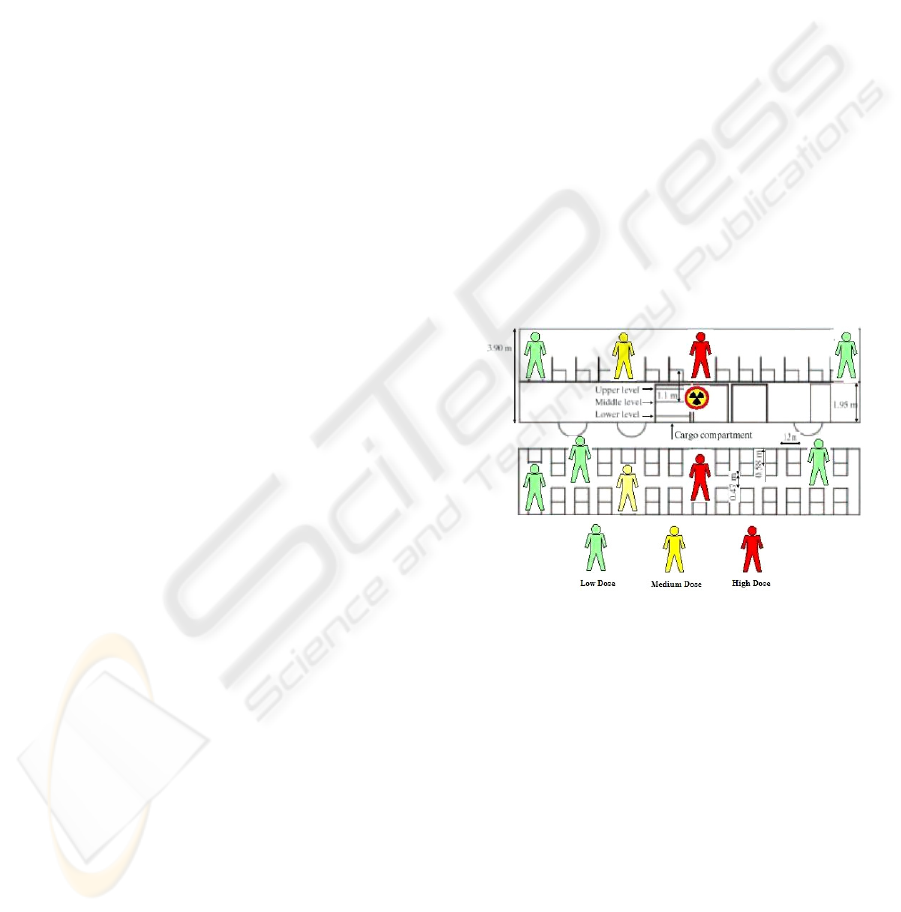
Figure 1: Bus passenger.

Figure 1. shows the relative distance between the

passengers and the source, as well a classification of

doses received.

“The time frame of the exposures of the bus

passengers is reasonably well defined. For most of

the passengers on the bus that day, this is an eight-

hour period from 16:00 to 24:00. There are some

variations on this; for example, the duration would

have been 30 minutes shorter for those passengers

picked up at Quilacollo and it would have been

longer for those passengers from Cochabamba who

spend some time on the bus before it departed. Also

some time would have been spent off the bus during

a meal stop

” (IAEA, 2004).

In our Agent-Based simulation we employed

essentially the same formula (equation 2) for doses

ICEIS 2007 - International Conference on Enterprise Information Systems

438

estimation. However, we summed 14 cm to the seat

heights, for the whole body dose may be better

represented at an eight of about one third of the way

up the torso (see table 1).

The received dose (d) for the passengers, after

reconstruction of the dose and technical analysis

conducted by an IAEA technical mission, was

calculated between a minimum 10mGy (~DE =

10mSv) to a 190 maximum mGy (~DE = 190 mSv)

for 8 hours of the bus trip (See table 2). The dose

received annually for the worldwide population due

to natural radiation is calculated in 1,12 mSv/year

and in the case of a source of

192

Ir, it is necessary

only 4 seconds of exposure to surpass the limit of

annual dose (1,12mSv/year).

As we can see from tables 1 and 2, the

simulation gave us upper limits for doses absorbed,

basically for not considering shield effects.

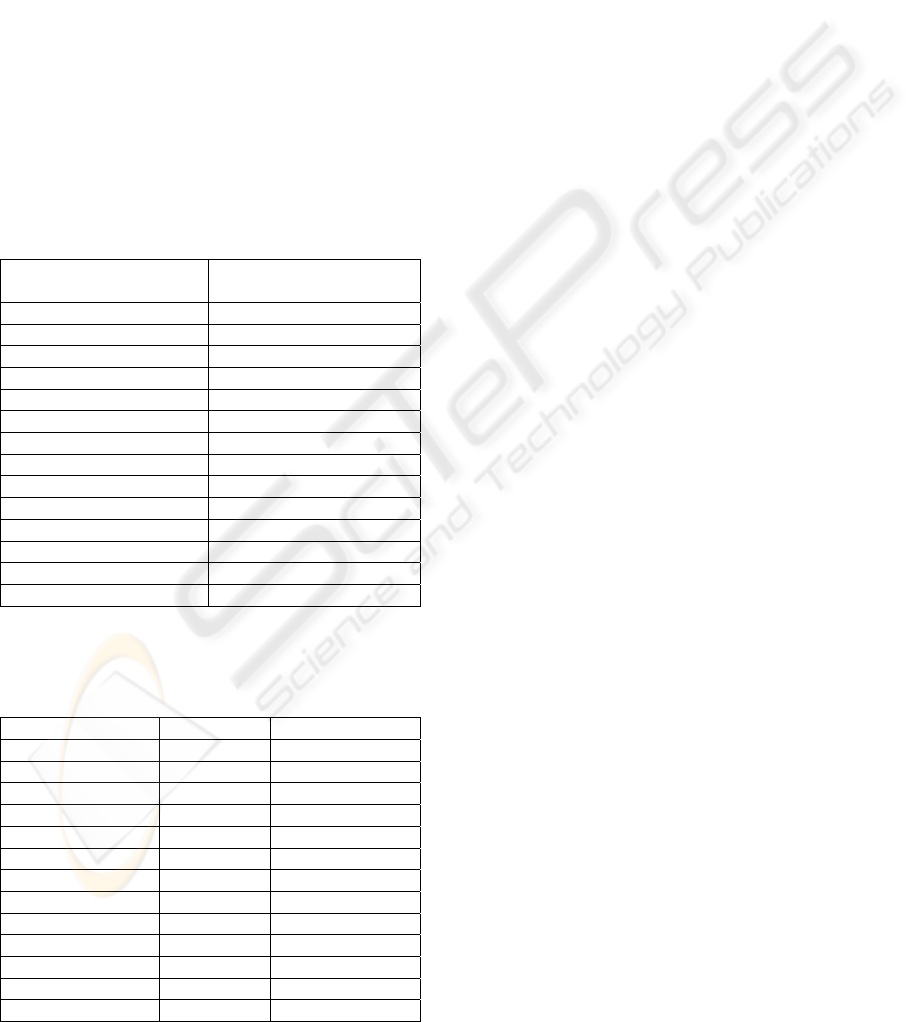
Table 1: Ranges of estimated doses (Gy) to the bus

passengers by Software Agent Simulation.

Seat number High Dose

(Agent simulation)

1–4 0.02

5–6 0.03

7–10 0.04

11–14 0.07

15–18 0.13

19–22 0.31

23–26 0.85

27–30 1.08

31–34 1.00

35–38 0.40

39–42 0.16

43–46 0.09

47–50 0.05

51–55 0.03

Table 2: Ranges of estimated doses (Gy) to the bus

passengers based on the dose reconstruction performed by

the IAEA team (IAEA, 2004).

Seat number Upper Lower

1–6 0.010 0.001

7-10 0.015 0.002

11-14 0.025 0.005

15-18 0.040 0.010

19-22 0.070 0.020

23-26 0.160 0.040

27-30 0.190 0.050

31-34 0.160 0.040

35-38 0.070 0.020

39-42 0.040 0.010

43-46 0.025 0.005

47-50 0.015 0.002

51-55 0.010 0.001

5 CONCLUSIONS

Trough this case study we could have a first idea of

the magnitude of the radiological accident and its

impact.

Simulating the number of people contaminated

by agent-based systems we can estimate the

absorbed doses, its spatial distribution and possible

physical consequences by the effect of the radiation.

The researcher can simulate a non-natural

radioactive dispersion, building an environment, in

a delimited area, where he can find parameters for

analysing and studying the phenomenon.

REFERENCES

Wooldridge, M. J., 2002. An Introduction to MultiAgent

Systems. John Wiley & Sons, Ltd, April.

Franklin, S. , Graesser A., 1997. Is it an agent, or just a

program?: a taxonomy for autonomous agents. In

Inteligents Agents III: Agent Theories, Architectures,

and Languages, edited by J. P. Muller, M. J.

Wooldridge, and N. R. Jennings, Berlin: Springer,

pp.21-35.

Farias, O. L. M, Leite, L. T, 2005. Simulation and

Control of Maritime Area through Multi-Agent

Systems and Geographical Information Systems . In:

International Conference on Intelligent Agents, Web

Technologies & Internet Commerce - IAWTIC 2005.

Vienna. Proceedings of the International Conference

on Intelligent Agents, Web Technologies and Internet

Commerce - IAWTIC'2005. Los Alamitos, California :

Edited by M. Mohammadian, v. 1. p. 734-738.

IAEA, 1996. Radiation Safety, Vienna, Austria.

Agape, A.M. , Arutyunyan, R.V., Yu.Kudrin, A., Eliseev,

A.M., 2005. Experience of past radiation accidents

and problems of response to possible dispersion of

radioactive material in urban conditions.

International Conference on the safety and security of

radioactive sources towards a global system for the

continuous control of sources throughout their life

cycle.

IAEA, 2004. The Radiological Accident in Cochabamba.

Vienna, Austria.

EMPLOYING SOFTWARE MULTI-AGENTS FOR SIMULATING RADIOLOGICAL ACCIDENTS

439