INFORMATION SYSTEM REQUIREMENT ANALYSIS

AND SPECIFICATION IN FOREST MANAGEMENT

PLANNING PROCESS

Salvis Dagis

Faculty of Information Technologies, Latvia University of Agriculture, Liela Street 2, Jelgava, Latvia

Keywords: UML, Process Modelling, Requirement analysis.

Abstract: Forests cover up to 45% of the territory of Latvia and forestry is the most significant export sector in Latvia.

The share of forestry in the country’s Gross Domestic Product is up to 14%. In order to manage the forests

economically efficiently it is necessary to plan the management activities for several decades in advance.

The forecasting of tree growth takes an important place within the forest management planning process.

In order to develop IT solution for the process of forest management planning, it is necessary to perform the

analysis of forestry sector, as a result of which the above models and also corresponding static structure are

developed. For their development, the Unified Modelling Language (UML) specification and notation are

used.

1 INTRODUCTION

Forestry is the leading sector of the national

economy of Latvia. The increase of its efficiency is

connected with the application of latest information

technologies in forest management and planning in

private and state forests. Taking into consideration

the real criteria, the planning of forest management

is a complicated and non-formalized process

therefore, in order to tackle this problem, it is

necessary to use IT solutions - such as object-

oriented modelling with the application of the

methods of artificial intelligence.

The necessity for the forecast of forest

development several decades in advance is

connected with the ensuring of sustainable forest

management planning (FMP). Since FMP process is

closely related to the time factor, the knowledge of

forest estimation data after a particular period of

time is an integral part of this process. Therefore

there are solutions needed for the forecasting of tree

growth process. The laws and regularities of the

growth of forest stands form the theoretical basis for

the forest management and are indispensable for the

solution of several practical issues: determination of

forest readiness (maturity), optimal felling cycle,

choice of felling systems and its intensity, as well as

target species for reforestation and afforestation, etc.

The aim of the paper is to develop IT solution for

the optimization of FMP process. The following

enabling objectives are set: the system analysis of

FMP processes; the modelling of FMP processes,

including tree growth motion prognoses.

2 MODELLING

FORMALIZATION OF FMP

PROCESS

Upon completion of the system analysis of FMP

processes, it turned out that the model of FMP

process (Use Case), as well as the corresponding

static structure, should be developed. A significant

part of the research is the modelling of FMP process,

as a result of which the model of tree growth process

should be implemented (embraced by FMP IS). The

model of forest stand growth process is related to the

actualization of the following estimation data: the

age of forest stand, average height and diameter, the

cross area of forest stand, the division of trees into

subclasses according to the diameter, the number of

tree stems per hectare, species composition and the

quality of timber.

574

Dagis S. (2007).

INFORMATION SYSTEM REQUIREMENT ANALYSIS AND SPECIFICATION IN FOREST MANAGEMENT PLANNING PROCESS.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - ISAS, pages 574-579

DOI: 10.5220/0002388505740579

 SciTePress

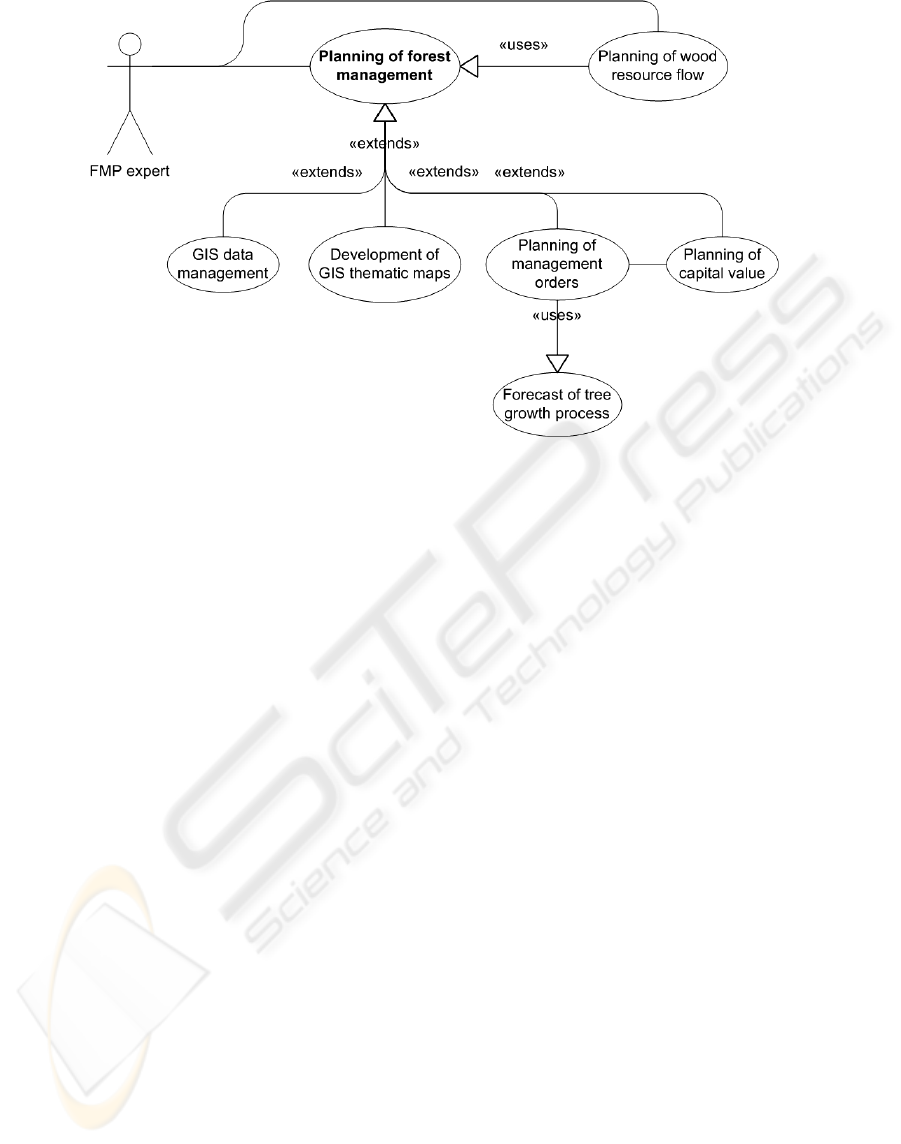
Figure 1: The dynamic model of FMP process.

2.1 The Dynamic and Static Models of

FMP

The first step in the development of the system is

defining requirements for the latter. As a result,

there is the preceding model developed. The model

is an excellent instrument for negotiation with the

potential user about the system from the user’s

position. It is defined what the system intends to

perform. The system requirements are the guidelines

for its testing and assessing during the entire

development process, as a result of which a

qualitative system is obtained.

The forest management planning is performed by

Actor – FMP expert (Fig. 1). This expert develops

strategic plans by means of FMP algorithms and

capital value algorithms. The above “Planning of

capital value” is the basis for strategic plans, because

the tactic and operational planning result from them.

It is closely related to the tactic planning (“planning

of management orders”), which suggests performing

the following activities in the forest: reforestation of

main felling, standing timber felling, forest stand,

cultivation of young stands, etc. During the process

of the planning of management orders, one should

observe the Regulations issued by the Cabinet of

Ministers, which contain restrictions on certain

management activities (the age and diameter of the

main felling, the maximum width and area of clear

cut, the cross area to be left after sanitary cut, and

other, regarding especially protected areas, etc.). A

significant part of the restrictions on the forest

management is related to the information analysis of

geographic information system (GIS). Forest

management plans, obtained at the operational

planning level, are used to plan the wood resource

flow (Oss, 2006) – it is where the transport cost is

calculated and the wood resource flow

recommended.

The above “GIS data management” ensures the

correct input, modifying and mapping of GIS data.

This is important because it supplements the

functionality of GIS with the logic of forest

territorial division (Dagis 2006a) and specific

functions of space analysis.

The “Development of GIS thematic maps”

envisage to facilitate the planning expert’s functions,

so that he knows the forest territories and their

detailed description better. If the expert uses

thematic maps, there is no need to see the estimation

data of each sub-plot. It is possible to interpret the

estimation data graphically, according to the

requested criteria and thus develop thematic maps.

When combining several thematic maps (the layers

of GIS thematic maps), the group of thematic maps

is formed. At this point, the data can be already

analyzed according to several groups of criteria (the

interlayer GIS data analysis).

The static models form the architectural basis of

system. The diagrams of UML classes show the

system classes with attributes and operations, as well

INFORMATION SYSTEM REQUIREMENT ANALYSIS AND SPECIFICATION IN FOREST MANAGEMENT

PLANNING PROCESS

575

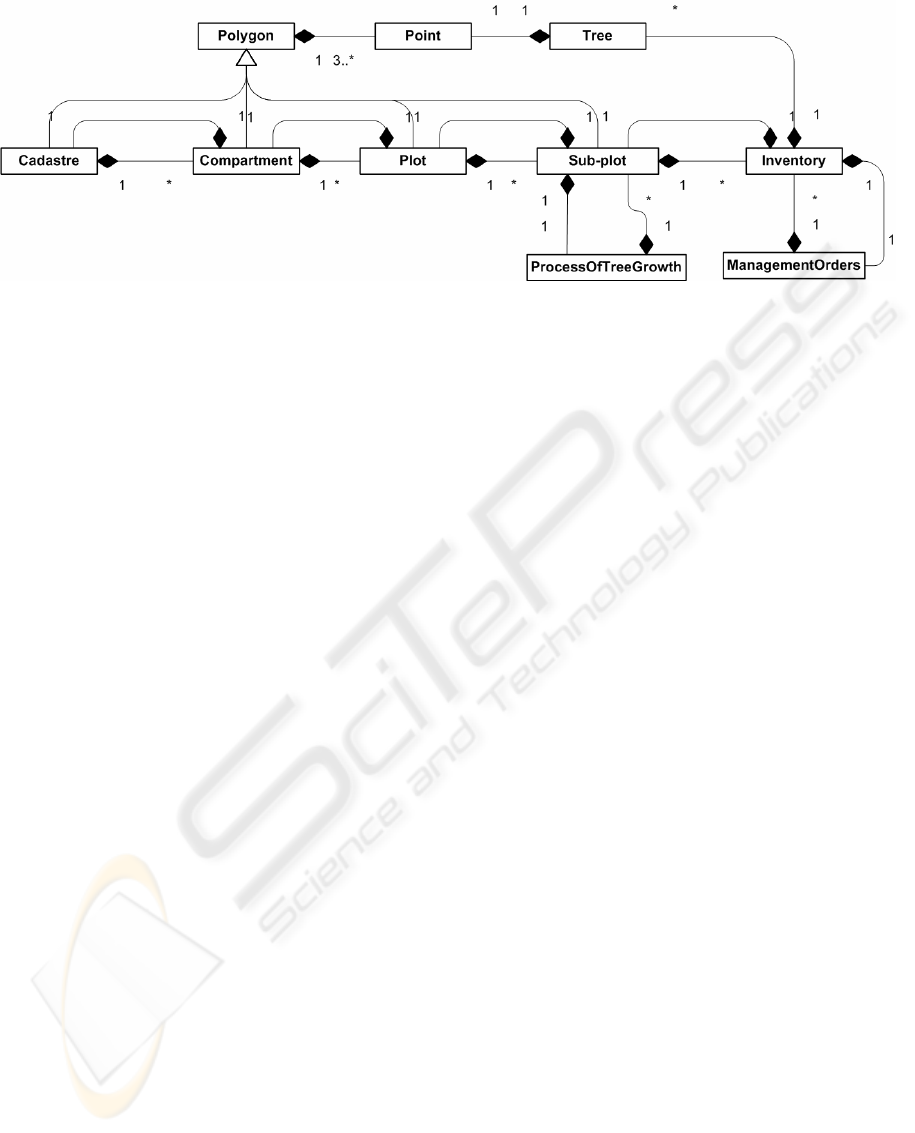
Figure 2: The static model of FMP process.

as the relations between classes. The diagrams of

classes are usually used to define the concepts of

research area, for the analysis of conceptual

requirements and the process of object-oriented

software development. In this case, the static model

shows the interaction of research objects and their

mutual relations. The essence of FMP process is the

management orders, which form the basis for the

planning of capital value, thus, the static structure of

the above is developed (Fig. 2).

In each Cadastre there is one or several

Compartments, each Compartment belonging

to only one Cadastre. Similar correlations exist

between Compartment and Plot, Plot and

Sub-plot. All these classes of territorial division

are inherited from the class Polygon. This ensures

the possibility for data analysis with the GIS

methods, which are from at least 3 or more points (x

and y coordinates). Sub-plot is the base unit of

forest territorial division, Inventory is related to

Sub-plot. One Sub-plot can have several

Inventories. Together with the

ManagementOrders, they form Sub-plot

history. Storage of the historical information in the

system gives opportunity to compare the forest

development and economic actions in time

dimension, which, in the FMP process, gives

adequate results. Inventory forms from inventory

or inventory update process. Inventory is a set of

trees, where each tree is geographically represented

by a point. Each tree has attributive information

(species, age, height, diameter).

In the process of management order planning,

FMP expert uses territorial plans and forest

estimation data. The activities that comprise this

process, basically are carried out using the territorial

elementary entities of forest – sub-plots (in special

cases they are combined or divided into several

Sub-plots). A Sub-plot is a forest territory

featuring trees with similar estimation indications

(Sile 2006). FMP process is complicated and

resources consuming, because a great number of

FMP criteria, Regulations, issued by the Cabinet of

Ministers, and forest owner’s aims should be taken

into account. The planning of management orders is

mostly based on the analysis of estimation data and

territorial restrictions. The estimation data should be

topical within the planning process. The estimator’s

responsibility is to actualize the estimation data

under real conditions once in 5-10 years, i.e. to visit

the particular territory of forest and to perform the

re-estimation. During these 5-10 years the

development of forest continues, but the estimation

data in the database do not change. It creates the

potential error in FMP results. In order to avoid such

error, it is necessary to update the estimation figures

(without involving the resources of estimators),

which in this case is modelled by the class

ProcessOfTreeGrowth. One Sub-plot has

only one tree growth motion (class

ProcessOfTreeGrowth), but one tree growth

motion can belong to several Sub-plots

2.2 Modelling of FMP Processes

The model is a simplified description or the

abstraction of reality. It is usually simplified,

because reality is too complicated to be copied

precisely. When developing simplified models, the

main factors of influence are taken into account,

while the insignificant ones are eliminated. When

modelling processes, one should take into

consideration the following basic principles: the

developed models should reflect the actual situation

precisely enough; the structure of models should be

ICEIS 2007 - International Conference on Enterprise Information Systems

576

the one, which could be substantiated and used for

the modeling of real processes. Mathematical or

quantitative models are developed, when it is

difficult and time-consuming to develop the physical

model. Within the decision support systems the

analysis is often performed numerically by means of

mathematical models. The main reasons to use the

mathematical models (Turban, 1988):

• They enable to analyze a great, and

sometimes unlimited, number of possible

solutions.

• They help to save time. The operations,

which in reality take several years, can be

performed in a shorter period of time using

computer.

• It is easier to manipulate the model (change

its parameters) than with a real system. It is

easier to carry out experiments, the results of

which do not affect the real system.

• The costs of errors, made during the

experiments, are relatively lower than of

those, made regarding real systems.

• The models enable to calculate the risk of

specific activities.

• The costs of modelling are relatively lower

than similar experimental costs of real

systems.

• It is easier to show the obtained results of

mathematical models graphically – easy to

understand for everybody.

One of the most commonly used actualization

mathematical models of forest stand estimation

indicators in Latvia does not provide the result

necessary for FMP process. For example, when

actualizing average height and diameter of forest

stand, the linear regression model of tree growth

process is used H(A+10) = a0 + a1 * H(A). It is

stated that this model can be used only for the period

of time, which is not longer than 10 years. Thus it

does not solve the planning problem, where the

estimation data should be actualized for the present

moment and several decades in advance. At present

widely applied model is linear and consists only of 2

parameters (a0 and a1), where the values are

determined by the expert. Parameter a0, as a matter

of fact, already shows the imperfection of the model,

because the dimensions of any growing thing (height

and diameter) at the age of 0 are equal to 0.

Parameter a1 indicates the rapidity of the increase of

starting value. This model functions very well for

the data actualization for a short period of time, i.e.

the non-linear phenomenon could be described

within the short interval by means of linear

coherence. However, there emerges a problem

concerning the use of these coefficients for the

particular forecasting of tree growth process for a

longer period of time, because the tree growth

process within the full growth cycle is characterized

by the non-linear coherence. Therefore, it would be

necessary to determine the coefficients of linear

equation repeatedly with a set step, if this model is

used for a different age of forest stand.

The laws of forest growth that we know at

present, do not fully reflect the essence of

phenomena, and they have stochastic nature. Taking

into consideration the great variety of nature, it is

rather difficult to find the functional coherence in it.

Therefore a law, defined mathematically, also

characterizes a separate object only approximately.

In order to describe any regularity in a mathematical

form (as a mathematical formula), it is necessary,

first of all, to find a general form of this

mathematical formula and then, using the

experimental data, calculate the parameters of this

formula. The level of modern computer engineering

(software provision) enables to calculate the

parameters of formulae without any difficulty, while

the informed choice of the general form of equation

is a yet unsolved problem. It is especially related to

the multiple stochastic coherences, which one often

comes across in the research in the area of modelling

growth process. In case with mathematical models, it

is necessary to describe the conditions, under which

these models are characterized by persistent

functioning and are able to provide correct results.

A research performed recently, (Dagis, 2006b)

concerns the mathematical models of tree growth

process, where the following non-linear regression

models of these process were studied:

y(t) = a·t

+ b·t

+ c·t (1)

y(t) = y

·e

-b·t

(2)

y(t) =a·t

/ (b

) (3)

The third polynomial level (1) is viewed, as it

provides good correlation coefficient within the

process of approximation. The polynomial

coefficient has no biological meaning and it does not

represent any growth model, therefore its application

is irrelevant. The exponential model (2) has

biological meaning, it models the limit of tree

growth in time: when increasing the age of tree

growth t, the speed of growth has a tendency

towards zero. But, unfortunately, when

approximating, the correlation coefficient is not as

good as it is in case with Power model (3). Power

model excellently approximates experimental data

with a good correlation coefficient. This

mathematical model was determined as the best one

for the further use to model the tree growth process.

INFORMATION SYSTEM REQUIREMENT ANALYSIS AND SPECIFICATION IN FOREST MANAGEMENT

PLANNING PROCESS

577

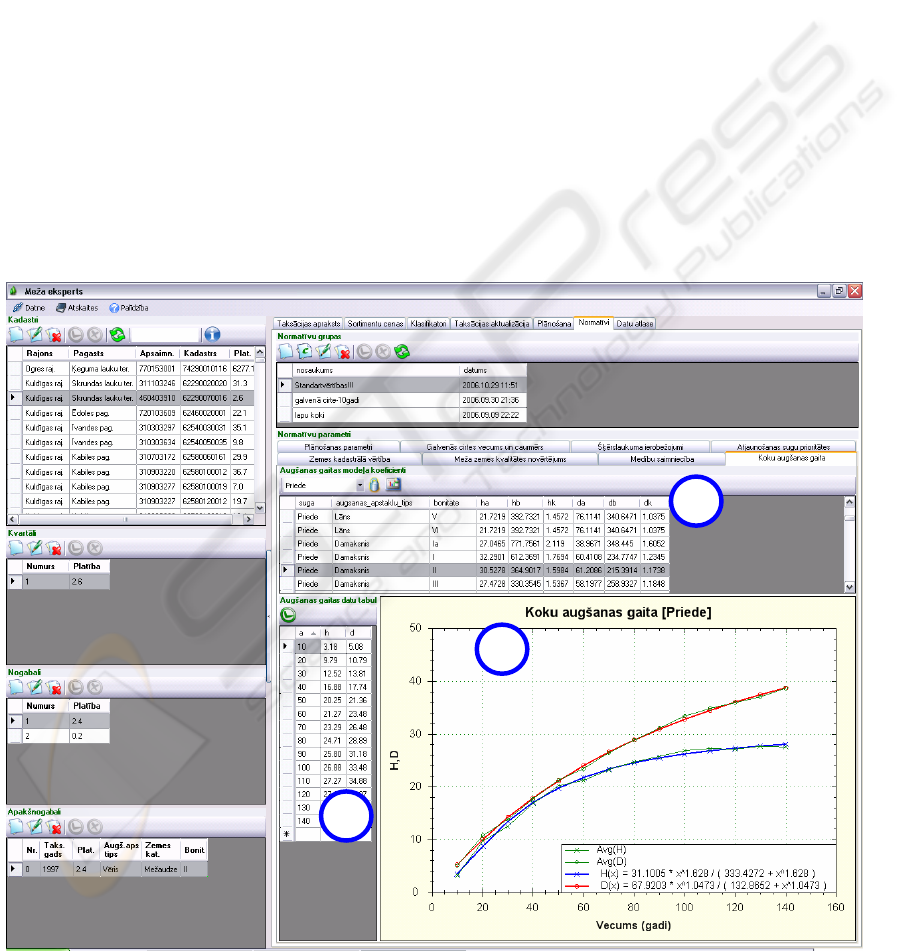
3 RESULTS

The static model of FMP process was implemented -

FMP IS “Forest expert”. This IS was developed as a

result of several research projects and at present

serves as an instrument of FMP process.

The implementation of forest territorial division

static structure is shown in Figure 3, where, on the

left, there is the forest territorial division (cadastres,

compartments, plots, sub-plots), but on the right –

the implementation of the above mentioned

mathematical Power model of tree growth process

with the real estimation data. These estimation data

are obtained from several districts of Latvia, with the

total area of 59,904 hectares, (41,056 sub-plots), the

prevailing species is pine (47% of total area), the

dominant types of growth conditions – pine forest

with Vacciniosa, Myrtillosa and Hylocomiosa forest.

Estimation data were obtained from 1999 till 2005.

These territories are mostly characterized by II

quality of locality (34% of total area), which is a

man-made division entity for the characterization of

forest stand productivity, determined by the tree

height at a particular age. Figures from 0 to 6

(usually – Roman numerals) are used to label the

quality of locality of stand. The highest quality of

locality is 0 or Ia, the lowest - 6.

In order to use the model of tree growth process,

it is necessary to specify the coefficients with the

input parameters, determined by the model. It is

necessary to choose the species, the type of growth

conditions and the quality of locality (Fig. 3, C). As

a result, the average contour line and diameter data

of forest stand, grouped by decades, are selected

from the available in the database (Fig. 3, A). On the

basis of the selected data, using Power model, the

coefficients of model are calculated, and the result is

shown as a graph (Fig. 3, B), where two curves

represent the real estimation data (tree height and

diameter) and another pair of curves shows the

approximated values of model.

Figure 3: IS implementation of the mathematical models of tree growth process.

ICEIS 2007 - International Conference on Enterprise Information Systems

578

This Power model functions under particular

conditions, i.e. the model characterizes the tree

growth process of chosen species under a particular

type of growth conditions and quality of locality,

therefore, it is necessary to calculate the coefficients

of mathematical model for all possible

combinations.

4 CONCLUSIONS

Using the dynamic model helped to define system

requirements for the execution of which the static

model was developed. One of the essential features

of the static model is the implementation of tree

growth by means of nonlinear mathematical model.

It was necessary to employ these models, because it

is impossible to perform experiments with a real

system – forest - within FMP process. Using

implemented mathematical model and adding to it

the statistically obtained coefficients, it is possible to

forecast the development of forest stands with

similar indications – in different types of growth

conditions and qualities of locality. The growth

process of trees is modelled with mathematical

equation y(t) =a·t

/ (b

), where the characteristic

is always increasing with 2 bending points,

therefore, it eliminates the occurrence of possible

incorrect data.

During the calculation process of mathematical

model coefficients, the following condition is to be

met: the data must be sufficient or, when grouping

data by decades, each decade should be represented

by at least 3 average estimation records – depending

on the limit of negligible forecast error. This

condition emerged, while testing model according to

particular estimation data, when it was stated that the

estimation data may have errors and deviations from

the average indicators, as long as there are particular

input parameters.

Such a model of growth process can be applied

to the analysis of difference in the forest growth

process of separate regions, as well as to the search

of incorrect, faulty estimation data in the existing

estimation database.

The static model of FMP process and

mathematical model of tree growth motion was

implemented (FMP IS “Forest expert”). Such a tree

growth motion forecast model can also be employed

in other states. For the complete ensuring of FMP

process, it is necessary to develop GIS module,

which would implement the territorial limitation of

FMP.

REFERENCES

Efraim Turban, 1988, Decision Support and Expert

Systems

Inita Sile, Sergejs Arhipovs, “The Development Of The

Precedent Model For The Latvia Forest Management

Planning Processes”, Proceedings, “8th International

Conference on Enterprise Information Systems”,

Cyprus, Paphos, 2006.

Janis Oss, "The model of wood resource flow",

Proceedings, "The 2006 European Simulation and

Modeling conference", Toulouse, France, 2006.

Salvis Dagis, Sergejs Arhipovs, “The static model of

Latvian forest management planning and capital value

estimating”, Proceedings, “8th International

Conference on Enterprise Information Systems”,

Cyprus, Paphos, 2006.

Salvis Dagis, Sergejs Arhipovs, Dagnis Dubrovskis - The

growth of trees motion mathematical models and their

adaptation the Latvia circumstances, Lithuania,

Kauno, 2006

INFORMATION SYSTEM REQUIREMENT ANALYSIS AND SPECIFICATION IN FOREST MANAGEMENT

PLANNING PROCESS

579