GROUP DECISION SYSTEMS FOR RANKING AND SELECTION

An Application to the Accreditation of Doping Control Laboratories

Xari Rovira, N

uria Agell

ESADE Universitat Ramon Llull, Av. Pedralbes 62, Barcelona, Spain

onica S

anchez, Francesc Prats

Universitat Polit

ecnica de Catalunya, Dept MA2, Jordi Girona, 1-3, Barcelona, Spain

Montserrat Ventura

Institut Municipal d’Investigaci

o M

edica (IMIM, IMAS), Doctor Aiguader, 80, Barcelona, Spain

Universitat Aut

onoma de Barcelona (UAB), Facultat de Medicina, Doctor Aiguader, 80, Barcelona, Spain

Keywords:

Qualitative reasoning, Group decision-making, Goal programming.

Abstract:

This paper presents a qualitative approach for representing and synthesising evaluations given by a team of

experts involved in selection or ranking processes. The paper aims at contributing to decision-making analysis

in the context of group decision making. A methodology is given for selecting and ranking several alternatives

in an accreditation process. Patterns or alternatives are evaluated by each expert in an ordinal scale. Qualitative

orders of magnitude spaces are the frame in which these ordinal scales are represented. A representation for the

different patterns by means of k-dimensional qualitative orders of magnitude labels is proposed, each of these

standing for the conjunction of k labels corresponding to the evaluations considered. A method is given for

ranking patterns based on comparing distances against a reference k-dimensional label. The proposed method

is applied in a real case in External Quality Assessment Schemes (EQAS) for Doping Control Laboratory

contexts.

1 INTRODUCTION

In group decision-making processes, the ranking or

selection of patterns depends on the judgments given

by the evaluators in the group. The group decision

method presented in this work is specially suitable

when aiming at an evaluation via qualitative ordinal

descriptions.

This work is a step further in terms of previous

works in the area of multi-criteria decision making

(Agell et al, 2006; Keeney, 1993) when information

is represented by absolute orders of magnitude la-

bels, such as ”very bad”, ”bad”, ”acceptable”, ”good”

and ”very good”. The proposed method is based on

the representation of the initial evaluators’ judgments

of each pattern via a k-dimensional label, which can

be seen as a hyper-rectangle, and its synthesis by

means of the distance to a reference k-dimensional

label. This in turn is based on a qualitative generalisa-

tion of a type of goal programming method known as

the reference point method for vectorial optimisation

and decision-making support (Gonza, 2001; Kallio,

1980).

In general, reference point methods for optimi-

sation in R

choose the points at a shorter distance

from a previously ﬁxed reference point as the opti-

mal alternative (the ”goal” to be reached) (Romero,

2001; Romero et al, 2001; Wier, 1980). In this

work, ranking in the set of existing patterns is per-

formed by selecting not a predetermined ﬁxed refer-

ence k-dimensional label, but a ”realistic” reference

for the problem to be solved: with respect to the nat-

ural order, the proposed reference hyper-rectangle is

the supreme of the set of available patterns, guar-

Rovira X., Agell N., Sánchez M., Prats F. and Ventura M. (2007).

GROUP DECISION SYSTEMS FOR RANKING AND SELECTION - An Application to the Accreditation of Doping Control Laboratories.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 82-87

DOI: 10.5220/0002389300820087

 SciTePress

anteeing consistency with the order between hyper-

rectangles. The distances between patterns and their

supreme give the ranking of patterns directly. More-

over, any problem of selection or accreditation of pat-

terns can be solved by using this ranking together with

a suitable threshold.

The proposed methodology may be of interest to

very different areas. Speciﬁcally, applications in can-

didate assessments (students in learning processes, re-

cruiting processes) as well as project management (ar-

chitectural, civil engineering and business projects)

can be considered. It may also be of interest in

decision-making processes in areas such as ﬁnance

and marketing.

The proposed method is applied in the evaluation

of data from an External Quality Assessment Scheme

(EQAS) of accredited doping control laboratories.

Laboratories involved in doping control have to be

accredited by both the World Anti-Doping Agency

(WADA) and by the national accreditation body fol-

lowing the ISO17025 quality standard (World Anti-

Doping Agency, 2004). This regulatory system is jus-

tiﬁed, on the one hand, to insure the highest quality

in analytical standards in beneﬁt of the athlete, and,

on the other hand, to harmonise quality standards in

laboratories regularly involved in legal disputes con-

cerning positive test results (i.e. a substance banned

by sport authorities). WADA accreditation is granted

after the evaluation of analytical data provided by lab-

oratories by an experts’ committee based on the in-

formation given to each expert, the judgments of each

evaluator and a further synthesis of these judgments.

Section 2 presents some features related to the

qualitative models of absolute orders of magnitude,

and Section 3 provides a qualitative representation

of patterns in a partially-ordered set. Section 4 in-

troduces the new group decision-making process by

deﬁnig a total order in the set of patterns in such a way

that the set of labels corresponding to the available

alternatives becomes a chain (ranking). The consis-

tency property for the ranking method is established.

In Section 5, the application to accreditation of dop-

ing control laboratories is given. Lastly, conclusions

and open problems are presented.

2 ABSOLUTE ORDERS OF

MAGNITUDE MODELS

The one-dimensional absolute orders of magnitude

model (Trave, 2003) works with a ﬁnite number of

qualitative labels corresponding to an ordinal scale of

measurement. The number of labels chosen to de-

scribe a real problem is not ﬁxed, but depends on the

characteristics of each represented variable.

Let’s consider an ordered ﬁnite set of basic labels

∗

= {B

,...,B

}, each one of them corresponding to

a linguistic term, in such a way that B

< ... < B

as for instance “very bad” < “bad” < “acceptable” <

“good” < “very good”.

The complete universe of description for the Or-

ders of Magnitude Space OM(n) is the set S:

S = S

∗

∪ {[B

] |B

∈ S

∗

,i < j},

where the label [B

] with i < j is deﬁned as the set

i+1

,...,B

The order in the set of basic labels S

∗

induces a

partial order ≤ in S deﬁned as:

] ≤ [B

] ⇐⇒ B

≤ B

and B

≤ B

. (1)

with the convention [B

] = {B

} = B

. This relation

is trivially an order relation in S, but a partial order,

since there are pairs of non-comparable labels.

3 PATTERN REPRESENTATION

IN A PARTIALLY ORDERED

SET

In the proposed group decision-making problem, each

pattern is characterized by the judgments of k eval-

uators, and these evaluations are given by means of

qualitative labels belonging to an orders of magni-

tude space. So, each pattern is represented by a k-

dimensional label, that is to say, a k-tuple of labels.

Let S be the orders of magnitude space with the

set of basic labels S

∗

The set of k-dimensional labels or patterns’ repre-

sentations E is deﬁned as:

E = S×

... ×S =

{

,...,E

) | E

∈ S ∀i = 1,...k

}

. (2)

Each k-dimensional label E = (E

,...,E

) is a set

of k qualitative labels (each one associated to an ex-

pert judgment) that deﬁne a pattern in such a way that,

on every component, the relation E

≤ E

means that

represents better results than E

This order in S is extended to the Cartesian prod-

uct E:

E = (E

,...,E

) ≤ E

′

= (E

′

,...,E

′

)

⇐⇒ E

≤ E

′

, ∀i = 1,...,k. (3)

E < E

′

, that is to say, E ≤ E

′

and E 6= E

′

, means

that pattern E

′

is better than pattern E.

This order relation in E is partial, since there are

pairs of non-comparable k-dimensional labels.

GROUP DECISION SYSTEMS FOR RANKING AND SELECTION - An Application to the Accreditation of Doping

Control Laboratories

E ≤ E

′

E  E

′

, E

′

 E

Figure 1: The partial order ≤ in E.

4 THE GROUP

DECISION-MAKING PROCESS

The proposed method for ranking or selection among

the existing patterns consists in :

• Fixing a distance d in E.

• Building a reference label

E: a proposition of con-

sistency determines that it has to be the supreme,

with respect to the order ≤, of the set of patterns

which are to be ranked.

• Assigning to each k-dimensional label E the value

d(E,

E); so, the patterns will be totally ordered as

a chain.

• This chain giving the ranking of the patterns di-

rectly. In an accreditation process, this chain,

along with a threshold, solves the problem.

• After this process, if a subset of the patterns is at

the same distance to

E, the same algorithm being

applied to this set, just beginning at the second

point.

4.1 A Distance in the Pattern

Representation Set

A method for computing distances between k-

dimensional labels is presented.

The ﬁrst step involves codifying the labels in S by

a location function (Agell et al, 2006). Through this

function, each element E

= [B

] in S is codiﬁed by

a pair (l

),l

)) of integers: l

) is the oppo-

site of the number of basic elements in S

∗

that are be-

tween B

and B

, that is to say, l

) = −(i− 1), and

) is the number of basic elements in S

∗

that are

between B

and B

, i.e., l

) = n − j. This pair of

numbers permits each element in S, where all differ-

ent levels of precision are considered, to be ”located”.

This “location” can be extended to any pattern de-

ﬁned by k orders of magnitude labels; the extension

to the set of k-dimensional labels E is:

L(E

,...,E

) = (l

),l

),...l

),l

)) (4)

which provides the relative position of a k-tuple of

qualitative labels with respect to the basis of E.

Then, a distance d between labels E,E

′

in S is de-

ﬁned via any metric R in R

and their codiﬁcations:

d(E, E

′

) = d((E

,...,E

),(E

′

,...,E

′

)) =

(L(E) −L(E

′

))

R(L(E) −L(E

′

)). (5)

This function inherits all properties of the distance in

4.2 Ranking of the Patterns

Starting from a distance d in E and a reference k-

dimensional label

E, a total order E will be deﬁned in

E, in such a way that the set of labels E

,...,E

cor-

responding to the available patterns becomes a chain

E ··· E E

, and so a ranking of the patterns is es-

tablished.

4.2.1 A Total Order in E

Let

E ∈ E be a k-dimensional label and let us call it

the reference label. Let d be the distance deﬁned in E

in Section 4.1. Then the following binary relation in

E  E

′

⇐⇒ d(E

′

E) ≤ d(E,

E) (6)

is a pre-order, i.e., it is reﬂexive and transitive.

This pre-order relation induces an equivalence re-

lation ≡ in E by means of:

E ≡ E

′

⇐⇒ [E  E

′

, E

′

 E]

⇐⇒ d(E

′

E) = d(E,

E). (7)

Then, in the quotient set E/≡ the following rela-

tion between equivalence classes:

class(E) E class(E

′

) ⇐⇒ E  E

′

⇐⇒ d(E

′

E) ≤ d(E,

E) (8)

is an order relation. It is trivially a total order.

In this way, given a set of patterns E

,...,E

these can be ordered as a chain with respect to their

proximity to the reference label: class(E

) E · · · E

class(E

If each class(E

), j = 1,...l, contains only the la-

bel E

, the process is ﬁnished and we obtain the rank-

ing E

⊳ · · · ⊳ E

. If there is some class(E

) with

more than one label, then the same process is applied

to the set of the labels belonging to class(E

), and

continued until the ﬁnal ranking E

⊳ · · · ⊳ E

obtained.

ICEIS 2007 - International Conference on Enterprise Information Systems

4.2.2 Consistency of the Ranking Method

The method of ranking via a distance to a reference

label previously selected is really necessary when the

order relation ≤ does not provide a total order in the

set of available patterns.

When the set {E

,...,E

} is totally ordered with

respect to ≤, that is to say, when a priori the patterns

are already ranked E

≤ ··· ≤ E

, then the proposed

method (via choosing of a suitable reference label)

has to reproduce the same ranking. This means that

the method has to be consistent.

Formally, the method will be consistent if the ref-

erence label

E is selected in such a way that:

(∀E

,...,E

∈ E)(E

≤ ··· ≤ E

=⇒

E ··· E E

) (9)

This requirement is equivalent to the following:

(∀E,E

′

∈ E)(E ≤ E

′

=⇒ EE E

′

) (10)

In effect, (9) =⇒ (10) is obvious. Reciprocally, if

(10) is satisﬁed, then when E

≤ ··· ≤ E

it sufﬁces

to apply (10) to each pair E

≤ E

i+1

Before establishing the way of choosing the refer-

ence label

E, in order for property of consistency to

be accomplished, let us compute the supreme of a set

of hyper-rectangles with respect to the partial order

≤ introduced in Section 3.

Given any E

,...,E

, let E

sup

be the supreme of

the set {E

,...,E

}, i.e., the minimum label in E

which satisﬁes E

≤ E

sup

,i = 1,··· ,l.

Its computation is as follows:

Let E

= (E

,...,E

), with E

= [B

] for all

h = 1,...,k, and for all r = 1,...,l. Then

sup

= sup{E

,...,E

} = (

,...,

where

= [max{B

,...,B

},max{B

,...,B

}], (11)

(see Figure 2).

sup{E

}

Figure 2: The supreme of a set {E

,...,E

Proposition 3 (of consistency) The ranking method is

consistent in the above sense if and only if, for any set

of patterns E

,...,E

, the reference label

E is chosen

as the supreme of the set {E

,...,E

Proof. If the label associated to any set of labels

is its supreme, statement (10) is trivial, because if

E ≤ E

′

then E

′

= sup{E,E

′

} =

E and d(E

′

E) = 0 ≤

d(E,

E), that is to say, EE E

′

To prove that it is necessary to choose the supreme

to assure the consistency, it sufﬁces to present as a

counterexample of (10) the case in which

E is not

the supreme. The easiest of these consists of the pair

E,E

′

, with E ≤ E

′

and

E = E. It is clear that E/E E

′

5 AN APPLICATION TO

ACCREDITATION OF DOPING

CONTROL LABORATORIES

There is considerable concern over the abuse of drugs

by athletes trying to improve their performance. Dop-

ing in sport is becoming increasingly sophisticated

and sampling methods and testing procedures vary

from one country to another. The absence of harmon-

isation in this area has led to an increasing number of

doping accusations being contested (Warmuth, 2002).

Establishing an external quality assurance scheme for

all Doping Control Laboratories is necessary to in-

crease the legal weight behind drugs tests and reduce

the number of positive drug tests being challenged in

the courts (Donike, 1992). Experimental data evalu-

ated in the present report were generated in the frame-

work of the EU funded project ALADIN 2002 (An-

alytical Laboratories for Antidoping Control: Inter-

national Network for External Quality Assessment),

coordinated by the Institut Municipal d’Investigaci

edica (IMIM) in Barcelona, in close collaboration

with the IOC laboratories in London (United King-

dom), Cologne (Germany) and Oslo (Norway), that

aims to develop the external quality assurance scheme

that would meet these needs. The group decision sys-

tem developed in this work is applied to summarise

the opinion of experts and to order the laboratories

involved in the study according to their quality.

5.1 Description of Data

Nine independent experts evaluated analytical data

provided by laboratories when analyzing samples

containing a banned substance (nandrolone) in sev-

eral rounds of the EQAS spread in four consecutive

years, according to their expertise. A total of 105 re-

ports generated by laboratories, were evaluated. Eval-

uations of each analytical report were rated as fol-

lows: Unacceptable; Insufﬁcient; Sufﬁcient; Good;

and Very Good. No intermediate scores were pos-

sible. All experts were management staff from four

GROUP DECISION SYSTEMS FOR RANKING AND SELECTION - An Application to the Accreditation of Doping

Control Laboratories

European IOC/WADA accredited anti-doping control

laboratories (King’s College London, United King-

dom; Hormone Laboratory in Oslo, Norway; Ger-

man Sports University in Cologne, Germany; and In-

stitut Municipal d’Investigaci

o M

edica in Barcelona,

Spain). All of the experts have excellent skills in the

analysis and evaluation of doping control samples and

they have more than ten years’ experience in this an-

alytical ﬁeld.

Each laboratory has initially been considered as

a 9-tuple of basic qualitative labels belonging to an

OM(5), where the basic elements are: B1= Unac-

ceptable, B2= Insufﬁcient, B3= Sufﬁcient, B4= Good

and B5= Very Good.The reference point -the ”opti-

mal laboratory”- is chosen as the maximum basic la-

bel assigned to all laboratories for each expert. Then

the distance, i.e., level of quality (LQ) from each pat-

tern to the optimal is used to rank the laboratories in

the sample. As shown in Section 4, LQ established a

total order in the set of laboratories, where the smaller

LQ is, the better The quality of the laboratory. As an

example, seven of the patterns are shown in Table 1, in

which distances to the optimal laboratory (LQ) and a

reﬁned order (RLQ) are included in the last columns.

As can be seen in Table 1, some patterns are

equidistant to the “optimal laboratory”. To avoid co-

incidence between distances as much as possible, and

to be able to discriminate laboratories, the group deci-

sion process is reapplied in each group with the same

level of quality, by deﬁning a new ad-hoc reference

point. In that sense, a reﬁned order of the initial set of

patterns (RLQ) is obtained. These can be seen in the

last column of Table 1 for the example considered.

It is important to notice that, although in this case

experts have been asked to evaluate each laboratory

with basic labels, this group decision methodology

can be considered with evaluations including differ-

ent levels of precision and even missing values.

5.2 Experiment and Results

According to the ratings assigned to the 105 reports

by the team of experts, these have been ﬁrst ordered

by LQ values. The distribution of the results obtained

is shown in Figure 3.

As it can be seen in Figure 3, there are 14 pairs

of indistinguishable laboratories with respect to their

distance to the ”optimal laboratory”, 7 groups of three

laboratories with the same LQ, 4 groups with four

laboratories equally ranked and 3 groups of ﬁve of

them. As an example, it can be considered the case

given in table 1 by the laboratories coded as #64, #65,

#55,#17,#70. These ﬁve laboratories have the same

LQ equal to 5,4, so they form one of the three groups

of ﬁve laboratories previously described. In a sec-

ond step, the 28 groups in which laboratories are not

distinguished are internally re-ranked and scored with

the RLQ value. Following the former example, table

1 shows the new values allowing a better distinction

in terms of their position to the ”optimal laboratory”.

This second step produces a ﬁnal order, making it pos-

sible to rank almost all the laboratories in the sam-

ple. At this point, if the group decision desired is a

binary classiﬁcation (in an accreditation process) ex-

perts will decide the LQ value to be considered as the

threshold.

Stem width: 1,00

Each leaf: 1 case (s)

Figure 3: Distribution of LQ values.

6 CONCLUSION AND FUTURE

RESEARCH

This paper proposes a methodology that synthesises

evaluations given by an experts’ committee. Evalua-

tions are considered in an ordinal scale, for this rea-

son a set of labels describing orders of magnitude is

considered. A group decision method is given in or-

der to rank the patterns based on comparing distances

to a reference k-dimensional label. The methodology

presented allows, on the one hand, the ordinal infor-

mation given by experts on the speciﬁc application to

be handled without previous normalisation, and, on

the other, the methods of “goal programming” to be

generalised without the need for previous knowledge

of the ideal goal.

The results applied to a real case show the appli-

cability of the methodology. In the experiment a set

of laboratories are evaluated by a group of experts

ICEIS 2007 - International Conference on Enterprise Information Systems

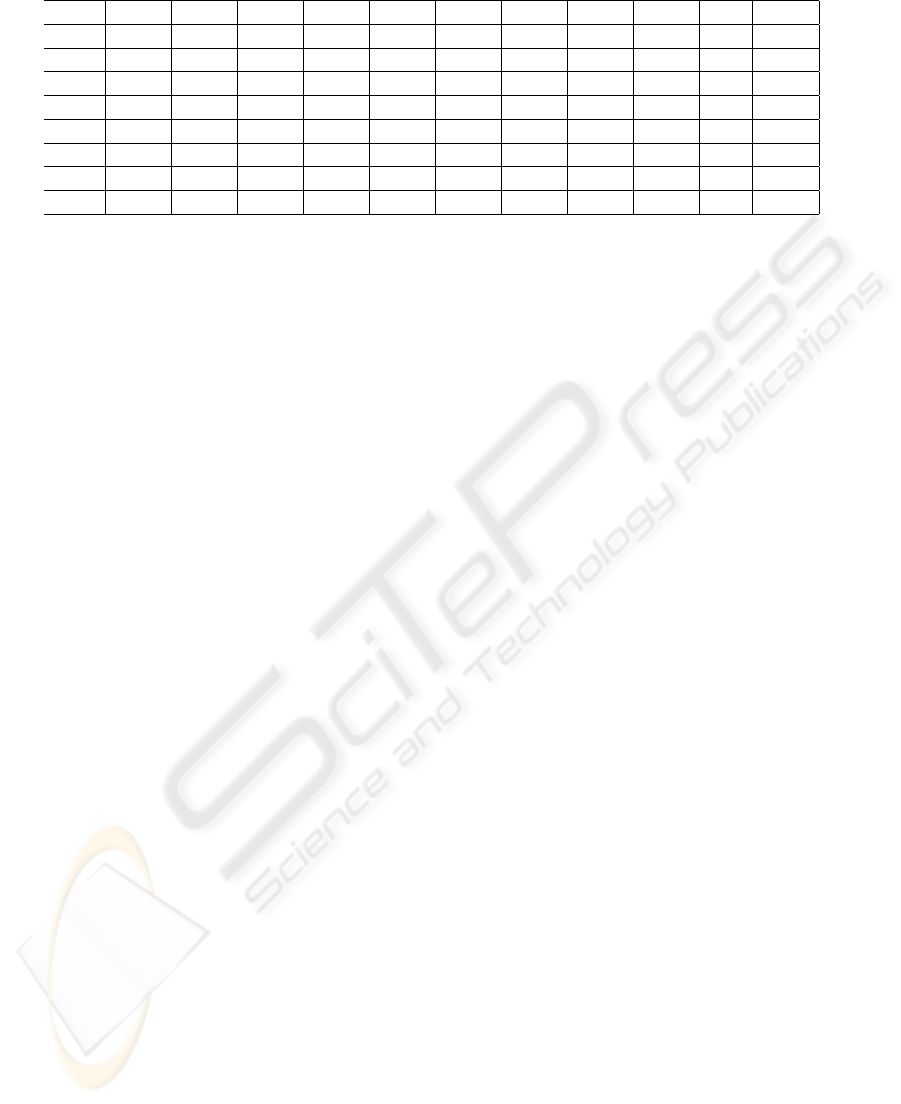
Table 1: Level of quality and Reﬁned level of quality.

code Exp1 Exp2 Exp3 Exp4 Exp5 Exp6 Exp7 Exp8 Exp9 LQ RLQ

105 B

3,4

74 B

3,7

45 B

4,0

64 B

5,4 2,8

65 B

5,4 2,8

55 B

5,4 4

17 B

5,4 4

70 B

5,4 4,5

that provide their individual inputs for some poste-

rior manipulation. It is important to point out that

the methodology presented allows imprecision in the

evaluations given by the experts to be considered.

As a future work the design of an automatic sys-

tem to perform the group decision process described

will be implemented. In addition, within the AURA

project framework, it is planned to build up an arti-

ﬁcial intelligence application that includes a learning

machine able to interpret and evaluate the laborato-

ries’ analytical reports and a software tool to imple-

ment the presented methodology.

ACKNOWLEDGEMENTS

This research has been partially supported by the

AURA research project (TIN2005-08873-C02-01 and

TIN2005-08873-C02-02), founded by the Spanish

Ministry of Science and Information Technology,

and by the EU Growth Programme (ALADIN 2002,

G7RT-CT-2000-05022). The authors would like to

thank Dr. Rafael de la Torre and Dr. Rosa Ventura at

Institut Municipal d’Investigaci

o M

edica (Barcelona)

for compiling the data used in this study and for their

helpful discussions and suggestions.

REFERENCES

Agell, N., S

anchez, M., Prats, F. & Rovira, X., 2006. Us-

ing Orders of Magnitude in Multi-attribute Decision-

making. In Proc. of the 20th International Workshop

on Qualitative Reasoning . Hanover, New Hampshire,

15-19.

Donike, M., 1992. Accreditation and Reaccreditation of

Laboratories by the IOC Medical Commission. In

First International Symposium on Current Issues of

Drug Abuse Testing.

Gonz

alez Pach

on, J., & Romero L

opez, C., 2001. ”Aggre-

gation of Partial Ordinal Rankings. An Interval Goal

Programming Approach”. Computers and Operations

Research. 28, 827-834.

Kallio, M., Lewandowski, A., & Orchard-Hays, W., 1980.

An Implementation of the Reference Point Approach

for Multi-Objective Optimization. In WP-80-35,

IIASA, Luxemburg.

Keeney, R.L., & Raiffa, H., 1993. Decisions with multi-

ple objectives preferences and value trade-offs. Cam-

bridge University Press.

Romero L

opez, C., 2001. Extended Lexicographic Goal

Programming: A Unifying Approach. The Interna-

tional Journal of Management Science, 29, 63-71.

Romero L

opez, C., Tamiz, M., & Jones, D., 2001. Com-

ments on Goal Programming, Pompromise Program-

ming and Reference Point Method Formulations:

Linkages and Utility Interpretations-A Reply. Journal

of the Operational Research Society, 52, 962-965.

Trav

e-Massuy

es, L., & Dague, P., 2003. Mod

eles et raison-

nements qualitatifs. Ed. Lavoisier, Hermes Science,

Paris, France.

Warmuth, R

atsch, G., Mathieson, M., Liao, J., & Lemmen,

C., 2002. ”Active Learning in the Drug Discovery

Process”. Advances in Neural Information Processing

Systems, 14. MIT Press.

Wierzbicki, A.P., 1980. The Use of Reference Objec-

tives in Multiobjective Optimization. In G. Fandel, T.

Gal (eds.): Multiple Criteria Decision Making; The-

ory and Applications, Lecture Notes in Economic and

Mathematical Systems. 177 Springer-Verlag, Berlin-

Heidelberg, 468-486.

World Anti-Doping Agency, 2004. The World Anti-Doping

Code. International Standard for Laboratories (ISL).

GROUP DECISION SYSTEMS FOR RANKING AND SELECTION - An Application to the Accreditation of Doping

Control Laboratories