IMPRECISE EMPIRICAL ONTOLOGY REFINEMENT

Application to Taxonomy Acquisition

ıt Nov

cek

DERI, National University of Ireland, Galway, IDA Business Park, Lower Dangan, Galway, Ireland

Keywords:

Ontology engineering, ontology learning, taxonomy acquisiton, uncertainty.

Abstract:

The signiﬁcance of uncertainty representation has become obvious in the Semantic Web community recently.

This paper presents new results of our research on uncertainty incorporation into ontologies created automat-

ically by means of Human Language Technologies. The research is related to OLE (Ontology LEarning) – a

project aimed at bottom-up generation and merging of ontologies. It utilises a proposal of expressive fuzzy

knowledge representation framework called ANUIC (Adaptive Net of Universally Interrelated Concepts). We

discuss our recent achievements in taxonomy acquisition and show how even simple application of the princi-

ples of ANUIC can improve the results of initial knowledge extraction methods.

1 INTRODUCTION

This paper builds on a novel representation of uncer-

tain knowledge in the scope of automatic ontology

acquisition, which was introduced in (Nov

cek and

Smr

z, 2006). The main objective of the ontology ac-

quisition platform OLE

is to implement a system that

is able to automatically create and update domain spe-

ciﬁc ontologies for a given domain. Ontologies are

used for many different tasks in the Semantic Web –

mainly for annotation of the web content, formal de-

scription of speciﬁc domains and reasoning on them.

As the amount of data on the Internet is vast and

dynamically growing and changing, we we empha-

sise an empirical approach to the ontology construc-

tion by means of bottom-up acquisition of concepts

from the domain-relevant resources (documents, web

pages, corpus data, etc.). The acquisition process

is incrementally boosted by the integration with the

knowledge already stored in the ontology.

The ontology engineering process is a difﬁcult

task. Manual efforts of collaborative ontology de-

sign (Gomez-Perez et al., 2004; Zhdanova et al.,

2005) lead to development of relatively precise and

complex ontologies, however, it is infeasible to cover

data intensive domains (e. g. medicine or computer

science) using only this approach to knowledge engi-

neering.

The project’s web page can be found at URL:

http:

//nlp.fi.muni.cz/projects/ole/

Therefore, automatic techniques (ontology learn-

ing (Buitelaar et al., 2005; Staab and Studer, 2004))

are needed to be applied in line with the collaborative

efforts. But they have another drawback – they are

not 100% correct, though they are generally broad in

coverage of the domain. There is obvious need for

tools that can reﬁne the possibly incorrect statements

in such ontologies before presenting them to users.

One way is to incorporate uncertainty into the learned

ontologies and select only the most important parts

according to the adopted uncertainty measure.

Besides the simple threshold-based reﬁnement of

the learned ontologies, there are also important cog-

nitive motivations of the utilisation of uncertainty in

our empiric ontologies that led us to the proposal of

a novel

ANUIC (Adaptive Net of Universally Interre-

ated Concepts) framework for representing uncertain

knowledge. This format can be easily applied in very

simple, yet effective reﬁnement of the results of on-

tology acquisition methods. The main contribution of

this paper is the presentation of initial results of appli-

cation of the ANUIC-based reﬁnement by integration

to taxonomy acquisition.

The structure of rest of the paper is as follows. We

brieﬂy recall the ANUIC model features in Section 2.

e go on describing the progress in our current re-

search in the meaning of new taxonomy acquisition

techniques implemented and more elaborate results

achieved (Sections 3 and 4). Section 5 brieﬂy resumes

related work. We conclude the paper in Section 6.

Novác

ek V. (2007).

IMPRECISE EMPIRICAL ONTOLOGY REFINEMENT - Application to Taxonomy Acquisition.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 31-38

DOI: 10.5220/0002391800310038

 SciTePress

2 DATA-DRIVEN ASSIGNMENT

OF FUZZY RELEVANCE

MEASURES IN ANUIC

Uncertain, and especially fuzzy semantics is consid-

ered as very important for the future development of

the Semantic Web (Sheth et al., 2005; Sanchez, 2006).

We work on development of such (formal) seman-

tics model within the

ANUIC framework. Currently,

a very initial proof of concept concerning the (auto-

matic) assignment

of reasonable fuzzy measures has

been implemented for our experiment in taxonomy

acquisition.

The implementation is based on a function that

assigns the relevance measure to a relation between

terms according to the frequency of the particular re-

lation in input data. The function deﬁnition is de-

scribed as follows.

Fuzzy appropriateness of a relation’s R element

, c

) ∈ R, where c

, c

are respective terms, is given

by a special function µ (derived from standard sig-

moid):

µ((c

, c

) ∈ R) =

1+ e

−s( f

((c

)∈R)−β)

where f

((c

, c

) ∈ R) =

f(O((c1,c2)∈R))

∑

c∈V

f(O((c1,c)∈R))

is the rela-

tive frequency of relation observations in input data

s is a parameter regulating the “steepness” of the func-

tion and β inﬂuences the placement of the inﬂexion

point. The domain of the function is real interval

(0, 1i (but only rational numbers obviously appear as

an input). The range is real interval (0, 1).

This function maps relative frequencies of respec-

tive observations in input data to the fuzzy appropri-

ateness measure of the relation. It can model various

natural characteristics of human mind like conserva-

tiveness, open-mindness (in the meaning of inﬂuence

of major or minor observations to the overall convic-

tion) and so forth

The function is continuous and thus can be im-

plemented in a very straightforward way. However, it

can easily imitate discontinuous jumps in the shape of

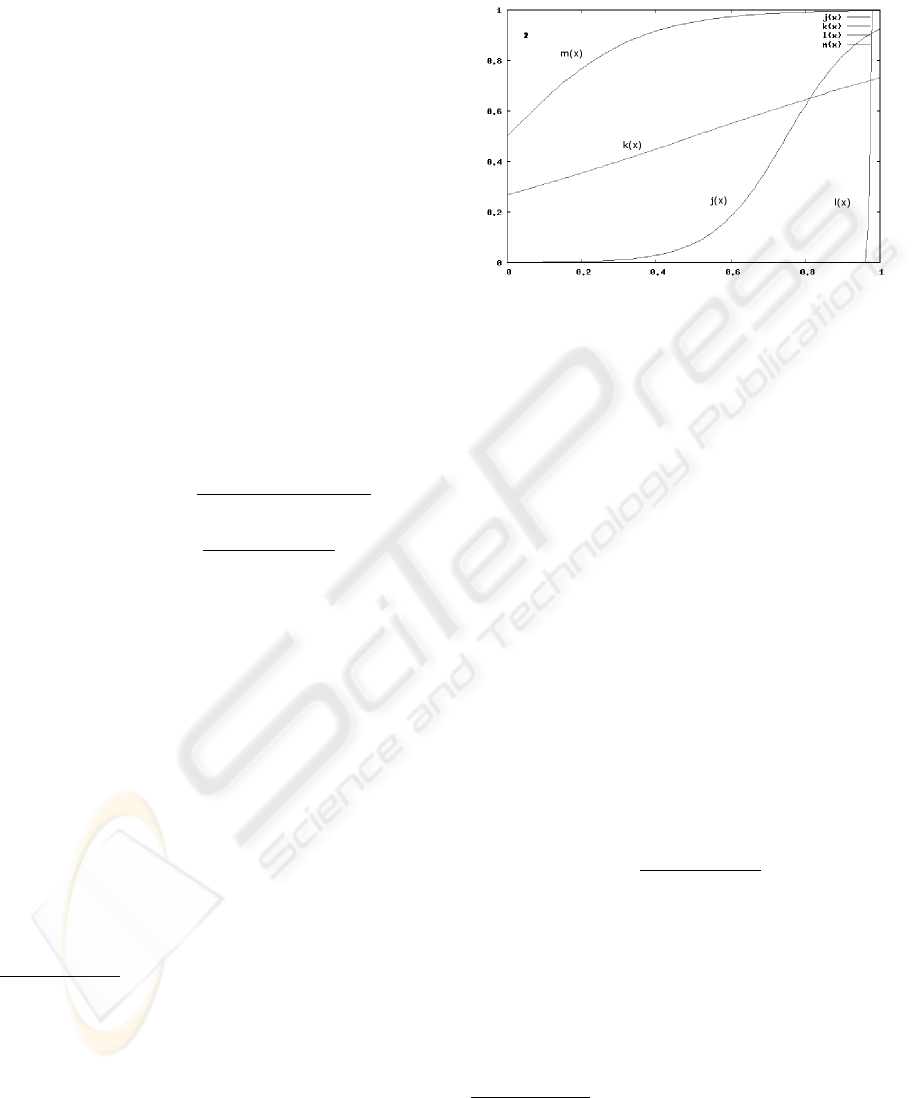
the curve, which is also very useful. Examples show-

Which was considered as an open problem to some ex-

tent in (Sheth et al., 2005).

This is rather an abstract, yet intuitive notation — the

O(Fact) expression stands for an observation of the Fact

in input data; the frequencies are absolute. The frequency

measure is not generally symmetric, as the relations them-

selves do not have to be symmetric.

One can, for example, ﬁx the meaning of a speciﬁc

group of terms and allow meaning variations for another

one.

ing shapes of the conviction function are displayed in

Figure 1

Figure 1: Examples of various shapes of the conviction

function.

One of the key properties of the

ANUIC format

is that it allows to naturally merge ontologies from

the same domain. When we have a large amount of

ontologies gained from a vast number of domain re-

sources, we can join them simply using their mutual

insertion into one complex

ANUIC structure. After

proper conﬁguration of the aforementioned function

parameters s, β, we obtain qualitatively different rep-

resentation of the domain – many formerly incorrect

relations are mostly marginalised, whereas the empir-

ically more valid relations obtain high relevance mea-

sures, signalising strong belief in their appropriate-

ness.

After several experiments with conﬁguration of

ANUIC parameters, we have found that a very good

heuristic for conﬁguration of the function parame-

ters is dynamic setting of the β inﬂexion point value.

The steepness parameter s was set to 100, which per-

formed best among various other settings.

The β for a term c and relation R is set as:

β =

|{ ˆc|(c, ˆc) ∈ R}|

Moreover, any relative frequency f higher than 0.5 is

adjusted by modifying the β parameter with 1− ( f −

0.5) expression. Only thus we obtain, for example,

natural conviction of (almost) 1 when we deal with

a single relation instance. Thus we can discriminate

very well between the relation instances with signiﬁ-

cant and insigniﬁcant frequencies due to the shape of

the conviction function

With the relative frequency and relevance measure on

the horizontal and vertical axes respectively.

Supposing that the higher the relation frequency is with

respect to the average relative frequency for relation edges

ICEIS 2007 - International Conference on Enterprise Information Systems

The process of integration of newly coming facts

is similar to the process of how people construct their

conceptual representations – ﬁrst they have almost

crisp evidence of a relation between objects (for ex-

ample that dogs have four legs). This opinion is

strengthened by further observations of four-legged

dogs, but one day they see a cripple dog having only

three legs. So they have to add another instance of the

“have-number-of-legs” relation, but with much more

decreased relevancy (unless they keep seeing other

and other different three-legged dogs). And this is a

simpliﬁed example of what we call continuous mean-

ing reﬁnement of conceptual models and what is hap-

pening also when the new resources are integrated

within the

ANUIC framework.

3 APPLICATION OF EMPIRICAL

REFINEMENT TO TAXONOMY

ACQUISITION

The technical description of application of our frame-

work in the taxonomy acquisition from English nat-

ural language texts is presented here

. We use the

well-known pattern-based technique (Hearst, 1992)

for creation of miniontologies from each input re-

source. These ontologies are

ANUIC-integrated then

in order to build a reference ontology that is exploited

by the consequent steps of complex taxonomy acqui-

sition. Section 3.1 elaborates our method based on ap-

proximate clustering that ensures signiﬁcant enhance-

ment in coverage. And eventually, the meta-algorithm

of conceptual reﬁnement is introduced in Section 3.2.

3.1 Clustering and Autonomous

Annotation

The clustering is very tempting in the scope of ac-

quisition of taxonomy of an ontology. The main idea

of this approach is to gain clusters of similar terms

and induce a hierarchical structure upon these terms

somehow. However, these approaches usually do not

offer a reliable automatic mechanism of annotation

of the resulting clusters that naturally correspond to

classes in an ontology.

coming from the c term, the more the relation is signiﬁcant

and vice versa.

We have concentrated on extraction of single general

terms in the presented experimental settings, but other tech-

niques of acquisition of more speciﬁc and multi-word terms

(like those in (Ryu and Choi, 2005)) can be easily incorpo-

rated as well.

We can obtain an initial domain ontology ontology

by integration of ontologies gained from particular re-

sources by pattern-based methods into the

ANUIC for-

mat (see Section 3.2 for details). Thus we obtain a

reference ontology that can be used for annotation of

clusters obtained from the same resources. The con-

tribution of such technique is obvious – we will dra-

matically increase the ontology coverage by incorpo-

ration of all signiﬁcant terms from the resources. We

have designed a method similar to k-means one-level

clustering, tuned to suit our demands in order to iden-

tify rough clusters in the input data.

3.1.1 Preprocessing Specialties

We require our platform to be scalable even for ex-

treme amounts of data. Therefore we are interested

also in efﬁciency of the clustering. The clustering

speed is signiﬁcantly inﬂuenced by the dimension of

the feature space.

We use quite a simple and standard metric of term

similarity given by a cosine distance between vec-

tors that represent their contexts. Given a set F =

{ f

, . . . , f

} of features, the vector V

= (v

, . . . , v

)

for term T is constructed this way:

• assign w

d−1

to v

, if feature f

is contained within

a vicinity of ⌈

⌉ from T; w ∈ (0, 1i is a prede-

ﬁned weight, CS is the relevant context size and d

is distance of the respective feature from T

;

• assign 0 to v

otherwise.

Following the main idea of the meta-algorithm pre-

sented in Section 3.2, we extract the initial concepts

from single resources of relatively small size and re-

ﬁne them further by empirical integration of the re-

sulting ontologies.

Therefore we can select features only from the

particular resources. We have tested several mea-

sures (like TF/IDF) for feature selection on the whole

domain as well as on the isolated resources, but we

have found out that a speciﬁc heuristics performs best

for our method. We simply discard hapax legomena

(terms with frequency equal to 1) from the resource’s

dictionary (without application of a stop-list, because

we would like to have the functional words in our

contexts as well). Thus we obtain a feature space

of dimension in range from 500 to 1, 500 for most

of the resources, which is satisfactory. The terms

When w = 1, the contexts are represented as bag of

words. When w < 1, their distance from term T is pro-

jected into the vector characteristics. The context size was

set to 14 – an average length of sentence in the resource

sets. Lower or higher context sizes were tried as well, but

without any signiﬁcant contribution. All the other parame-

ter settings used are further speciﬁed in Section 4.

IMPRECISE EMPIRICAL ONTOLOGY REFINEMENT - Application to Taxonomy Acquisition

themselves are extracted in a similar way – a gen-

eral English stop-list is applied and the terms with

frequency above a given threshold are considered as

terms. Frequency of 5 was found to be reasonable for

it does not eliminate any domain-speciﬁc words and

does not bring too many unwanted garbage-words in

most cases.

3.1.2 Simpliﬁed Rough Clustering

Several variants of k-means clustering are discussed

and brieﬂy analysed for example in (Kanungo et al.,

2002). General characteristic of all algorithms of this

kind is that they ﬁnd k points (centres) in the data

space that minimise average square distance of all

points in the data-set from these centres. Then the

clusters are usually deﬁned as a k-sized set of bal-

anced groups of points that are nearest to particular

centres.

Many algorithms ﬁnd a local minimum for the

problem in an iterative manner. We have found usual

implementation of k-means clustering unsuitable for

our reasons mainly due to their speed. We are not

very interested in optimality of our clusters. More-

over, the points in our data space are quite uniformly

distributed in most cases because of the restricted size

of the feature space and characteristics of natural lan-

guage that lay beyond the feature selection.

We have implemented a non-optimal (even lo-

cally), but very efﬁcient technique that provides us

with rough clustering of the initial resources that is

further utilised within the reﬁnement of ontologies

gained from particular resources

The method of simpliﬁed rough clustering is de-

scribed

in Algorithm 3 (given in Appendix).

3.1.3 Annotation

The consequent annotation of the clusters using the

reference ontology is sketched in Algorithm 1 (given

in Appendix).

3.2 Reﬁnement by Integration

The conceptual reﬁnement idea lies in integration of

small ontologies into bigger ones, smoothing many

The sub-optimality of clusters obtained by the tech-

nique is balanced by the efﬁciency and further empirical

reﬁnement in the resulting ontology model. However, the

technique presented here could be used for preparing rea-

sonable initial means and related reduction of iterations for

the classical k-means clustering methods, if needed.

Certain parts of the algorithm are put rather informally

due to simplicity of the description.

of the crisp and possibly incorrect relations by uncer-

tain empirical evidence from large number of obser-

vations. It is inspired by a simple analogy of human

mind and utilises the inherent dynamics and uncer-

tainty of the

ANUIC framework. Note that for the op-

timal performance of the

ANUIC-based integration, it

is needed to process at least tens of relevant resources

of a sufﬁcient size (hundreds or more words). We

should not await reasonable reﬁnement results when

providing only few documents with size of a couple of

sentences – even human learners cannot process such

small amounts of data in order to create a valuable

opinion about the domain’s conceptual structure.

Concrete application of the above mechanism to

the taxonomy acquisition is quite straightforward and

conforms to the abstract description in Algorithm 2

(given in Appendix).

We can easily update the domain ontology when

keeping the track of how a relation was obtained.

Thus we can still identify the more precise “refer-

ence” relations in the domain ontology D. We add

the new resource by processing it ﬁrst by the pattern-

based technique. Then we integrate the result into the

domain ontology and process the resource again by

clustering-based method, annotating the classes using

reference subset of D. The result of this step in then

integrated in D as well – the new resource is com-

pletely covered then.

4 SELECTED RESULTS OF

TAXONOMY ACQUISITION

In the following we describe some of the experiments

with taxonomy extraction in OLE and show their re-

sults. The improvement of the integration within the

ANUIC knowledge representation format is then illus-

trated in Section 4.2.

4.1 Extraction Phase and its Initial

Results

We tested the taxonomy acquisition on a sample of

3, 272 computer science articles, automatically down-

loaded from the web. The compound size of the re-

sources was 20, 405, 014 words. For the approximate

manual evaluation we randomly chose ﬁve ontologies

for respective resources from the whole set for each

run of a method.

Due to problems with evaluation of automatic

ontology acquisition (as expressed, for example,

in (Brewster et al., 2004)) we performed only a lim-

ited evaluation within the initial experiments. For

ICEIS 2007 - International Conference on Enterprise Information Systems

each selected ontology corresponding to a resource,

we computed precision as the ratio of “reasonable” re-

lations compared to all extracted relations

. The rea-

sonability of a relation was judged by a committee of

computer science experts and students after analysing

the respective resources.

The coverage was computed as the ratio of num-

ber of extracted signiﬁcant terms (nouns for the sim-

ple experimental settings) to all signiﬁcant terms

present in the resource. For all the measures of preci-

sion (Pr.) and coverage (Cov.), an average value was

computed. We present these results in Table 1, pro-

vided with respective average original resource size

and number of all concepts extracted.

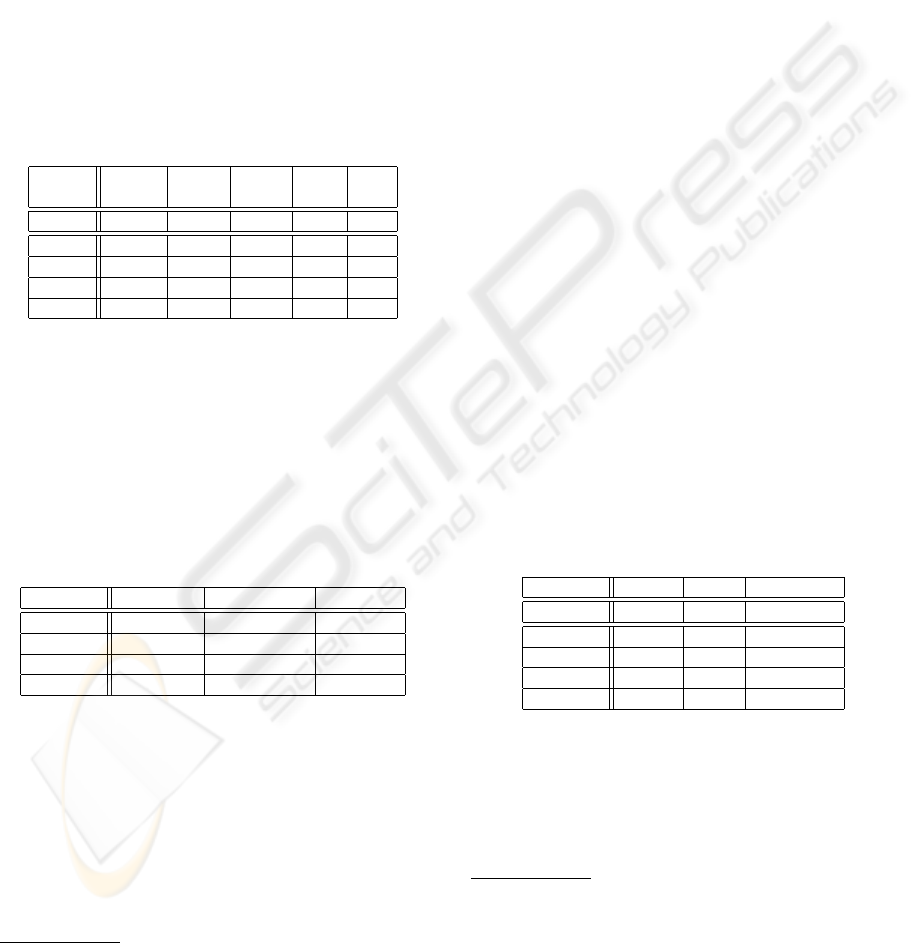
Table 1: Selected results of initial taxonomy extraction.

Method Res. sz. No. of No. of Pr. Cov.

(wrd.) conc. rel. (%) (%)

M1 4275 20.6 15.2 61.73 1.83

M2/S1 5777 138.4 1191.8 45.78 100

M2/S2 4669 106.2 494 33.11 100

M2/S3 4827 136.6 1336.2 46.13 100

M2/S4 5339 128.25 680 41.52 100

The M1 row contains results of pattern-based ex-

traction. The M2 rows contain results of clustering-

based method for respective parameter settings given

in Table 2. The rows’ headings present settings ID, in

the columns there are values of the respective param-

eters. The cluster size is used for derivation of the k

parameter for clustering algorithm.

Table 2: Settings for clustering-based method.

Settings ID Context size Position weight Cluster size

S1 14 1.0 10

S2 14 1.0 5

S3 14 0.7 10

S4 14 0.7 5

4.2 Improvement Obtained by

Uncertain Conceptual Reﬁnement

In order to produce reference ontology for the au-

tonomous cluster annotation, we generated ontologies

for each resource by pattern-based OLE module and

merged them into one

ANUIC structure. We used the

For the clustering-based acquisition only 50 randomly

selected relations were evaluated for each ontology, because

the average number of all relations was too high for manual

evaluation.

heuristics described in Section 3.2 for conﬁguration

of the parameters.

Using the

ANUIC-integration we gained a tax-

onomy with 5, 538 classes, 9, 842 individuals

and

61, 725 mutual is-a relations.

It is very hard to formally decide what is the repre-

sentation’s exact improvement when compared to the

knowledge stored in the former crisp ontologies. But

we can again give at least a rough picture – when we

considered only the relations with the highest fuzzy

relevance for a particular concept

, we can compute

an approximate ratio of “reasonable” relations simi-

lar to the one presented in Section 4.1. We computed

the ratio on a random sample of 50 relations from the

whole merged ontology and obtained the value 84 %,

which deﬁnitely shows an improvement.

The ontology gained by incorporation of results

of pattern-based method into

ANUIC was used as the

reference for clustering-based method. The results of

the

ANUIC merge of the source crisp ontologies for

both methods and various settings of the algorithms

are in Table 3 below.

We used the same merging parameters and crite-

ria of reasonability as for the creation and evaluation

of the reference ontology. Only the relations with the

highest conviction(s) were taken into account for eval-

uation. The precision computed on random sample of

50 relations from the merged ontology is given in the

latter

column. The average crisp precision for re-

spective source ontologies is in the Pr

former

column.

The improvement (in percents) is in the Improvement

column.

Table 3: Results of merging for clustering-based method.

Settings ID Pr

former

latter

Improvement

M1 61.73 84.0 136.08

M2/S1 45.78 65.52 143.12

M2/S2 33.11 65.38 197.46

M2/S3 46.13 63.16 136.92

M2/S4 41.52 64.07 154.31

The ontology with the best characteristics (gained

with S1 conﬁguration) was experimentally merged

with the reference ontology. Resulting ontology has

much higher range than the reference one – it contains

1, 584 classes

and 30, 815 individuals, intercon-

We empirically assume that a concept is an individual

as long as it has no hyponyms.

Which is by the way a very strong restriction, the range

of possible interpretations of the concrete conviction values

is much higher.

Some of the former classes were turned into individuals

– this is a direct consequence of the annotation algorithm.

IMPRECISE EMPIRICAL ONTOLOGY REFINEMENT - Application to Taxonomy Acquisition

nected by 1, 293, 998 relations in the taxonomy. The

approximate precision of the 50 randomly selected re-

lations with the highest conviction was 71.05 %. It is

of course slightly lower than the similar measure for

the reference ontology, but this is not a big drawback

when we consider the widely increased coverage of

the domain.

A sample from the resulting extended uncertain

domain ontology is given in Figure 2. The ovals rep-

resent classes, squares are individuals and arrows go

from sub-concept to its super-concept, labelled by re-

spective fuzzy relevance measures.

5 RELATED WORK

Our work is to some extent similar to the one pre-

sented in (Haase and V

olker, 2005) paper on uncer-

tainty handling in Text2Onto (Cimiano and V

olker,

2005). Text2Onto also utilises initial automated

knowledge extraction methods and integrates them

into so called Learned Ontology Model. It incorpo-

rates uncertain rating annotations of the gained re-

lations. A DL-consistent model is selected then as

a subset of the statements in the learned model ac-

cording to these annotations. On the other hand, we

deal with the inconsistencies internally and allow to

reason generally among all the gained knowledge un-

der different well-deﬁned perspectives. This provides

us with very valuable option of contextualised infer-

ences, among other things.

The reasoning perspectives of our paper are re-

lated to the work on fuzzy extension of OWL, which

is presented in (Stoilos et al., 2005). However, our

current research in automated

ANUIC-based reason-

ing with learned ontologies is somehow different from

this logical approaches and is motivated rather by the

more general AI paradigms of analogical (Paritosh,

2006; Hobbs and Gordon, 2005) and heuristic (Koki-

nov and French, 2003) reasoning. The transforma-

tions of

ANUIC into the current standard and fuzzy on-

tology representation formats (namely OWL (Bech-

hofer et al., 2004) and fuzzy-OWL (Stoilos et al.,

2005) have to be studied in more detail before we can

make proper conclusions and proceed with compar-

isons with traditional reasoning paradigms.

6 CONCLUSIONS AND FUTURE

WORK

The main contribution of this paper rests with the pre-

sented boost of initial ontology acquisition methods

by very simple application of the

ANUIC-based empir-

ical integration of learned knowledge. In this exper-

iment, we have provided an initial proof of concept

and groundwork for a novel ontology learning and

reasoning paradigm we are currently working on. The

full implementation of the related framework aims at

extension of ontology learning with robust, though

heuristic reasoning routines, that would enable rich

and meaningful inferences even for large learned on-

tologies. Thus we can help to shift on-line knowl-

edge acquisition, management and decision support

in data-intensive domains (such as medicine) to a

qualitatively different level.

Note that we have also implemented SOLE – a

web interface demonstrating the basic functionalities

of the current state of our OLE ontology acquisi-

tion framework. It processes documents (in plain

text, HTML, PDF or PostScript) uploaded by users

and creates (fuzzy) ontologies from them. It uses

the techniques described here. Users can also de-

ﬁne their own patterns for extraction of different se-

mantic relations than the taxonomical ones. The sys-

tem can be accessed at URL:

http://nlp.fi.muni.

cz/projects/ole/web/

. One can download a brief

manual for the system there. The preview credentials

for a testing public account with few pre-deﬁned rela-

tion patterns are test for user-name and test for pass-

word.

Our future work will focus on incorporation of re-

sults of another extraction methods to increase the re-

call and number of kinds of extracted relations. A

formal development and validation of a speciﬁc cal-

culus for

ANUIC-based reasoning engine is needed

then. The mutual correspondence and transformation

possibilities between ontologies in ANUIC format and

formats like OWL or fuzzy-OWL must be examined

as well, in order to thoroughly evaluate and compare

the framework to other similar tools and provide an

inter-operation layer by means of the Semantic Web

standards.

ACKNOWLEDGEMENTS

This work has been supported by the Academy

of Sciences of the Czech Republic, ‘Informa-

tion Society’ national research program, the

grant AV 1ET100300419, and by the EU IST

6th framework’s Network of Excellence ‘Knowledge

Web’ (FP6-507482). We would also like to thank

to Pavel Smr

z, who supported our research by his

general senior experience during the initial course of

our work within a master thesis.

ICEIS 2007 - International Conference on Enterprise Information Systems

Figure 2: Sample from the merged computer science ontology.

REFERENCES

Bechhofer, S., van Harmelen, F., Hendler, J., Horrocks, I.,

McGuinness, D. L., Patel-Schneider, P. F., and Stein,

L. A. (2004). OWL Web Ontology Language Refer-

ence. Available at (February 2006):

http://www.w3.

org/TR/owl-ref/

Brewster, C., Alani, H., Dasmahapatra, S., and Wilks, Y.

(2004). Data driven ontology evaluation. In Proceed-

ings of LREC 2004.

Buitelaar, P., Cimiano, P., and Magnini, B., editors (2005).

Ontology Learning from Text: Methods, Evaluation

and Applications. IOS Press.

Cimiano, P. and V

olker, J. (2005). Text2Onto - a framework

for ontology learning and data-driven change discov-

ery. In Proceedings of the NLDB 2005 Conference,

pages 227–238. Springer-Verlag.

Gomez-Perez, A., Fernandez-Lopez, M., and Corcho, O.

(2004). Ontological Engineering. Advanced Informa-

tion and Knowledge Processing. Springer-Verlag.

Haase, P. and V

olker, J. (2005). Ontology learning and rea-

soning - dealing with uncertainty and inconsistency.

In da Costa, P. C. G., Laskey, K. B., Laskey, K. J.,

and Pool, M., editors, Proceedings of the Workshop on

Uncertainty Reasoning for the Semantic Web (URSW),

pages 45–55.

Hearst, M. A. (1992). Automatic acquisition of hyponyms

from large text corpora. In Proceedings of the 14th

conference on Computational linguistics, pages 539–

545, Morristown, NJ, USA. Association for Compu-

tational Linguistics.

Hobbs, J. R. and Gordon, A. S. (2005). Toward a large-

scale formal theory of commonsense psychology for

metacognition. In Proceedings of AAAI Spring Sym-

posium on Metacognition in Computation, pages 49–

54, Stanford, CA. ACM.

Kanungo, T., Mount, D., Netanyahu, N., Piatko, C., Silver-

man, R., and Wu, A. (2002). An efﬁcient k-means

clustering algorithm: analysis and implementation.

Kokinov, B. and French, R. M. (2003). Computational mod-

els of analogy making. In Nadel, L., editor, Encyclo-

pedia of Conginitve Science, volume 1, pages 113–

118. Nature Publishing Group, London.

Nov

cek, V. and Smr

z, P. (2006). Empirical merging of

ontologies – a proposal of universal uncertainty repre-

sentation framework. In LNCS, volume 4011, pages

65–79. Springer-Verlag Berlin Heidelberg.

Paritosh, P. K. (2006). The heuristic reasoning manifesto.

In Proceedings of the 20th International Workshop on

Qualitative Reasoning.

Ryu, P.-M. and Choi, K.-S. (2005). An information-

theoretic approach to taxonomy extraction for on-

tology learning. In Buitelaar, P., Cimiano, P., and

Magnini, B., editors, Ontology Learning from Text:

Methods, Evaluation and Applications, pages 15–28.

IOS Press.

Sanchez, E., editor (2006). Fuzzy Logic and the Semantic

Web. Capturing Intelligence. Elsevier.

Sheth, A., Ramakrishnan, C., and Thomas, C. (2005). Se-

mantics for the semantic web: The implicit, the formal

and the powerful. International Journal on Semantic

Web & Information Systems, 1(1):1–18.

Staab, S. and Studer, R., editors (2004). Handbook on

Ontologies. International Handbooks on Information

Systems. Springer-Verlag.

Stoilos, G., Stamou, G., Tzouvaras, V., Pan, J., and Hor-

rocks, I. (2005). Fuzzy owl: Uncertainty and the se-

mantic web. International Workshop of OWL: Expe-

riences and Directions, Galway, 2005.

Zhdanova, A. V., Krummenacher, R., Henke, J., and Fensel,

D. (2005). Community–driven ontology management:

Deri case study. In Proceedings of IEEE/WIC/ACM

International Conference on Web Intelligence, pages

73–79. IEEE Computer Society Press.

IMPRECISE EMPIRICAL ONTOLOGY REFINEMENT - Application to Taxonomy Acquisition

APPENDIX

Algorithm 1 Cluster annotation with super-class

term.

Require: C — set of clusters

Require: t

hyperonymy conﬁdence threshold, 0.7 is reasonably discrimi-

native

Require: R reference ontology

Require: hyper(t,R, t

) — function that returns all hypernyms of t in R with

hypernymy relation relevance higher than t

Require: onto(C) — functions that returns an internal ontology representa-

tion equivalent to the annotated clusters

1: for c ∈ C do

2: H ←

0 {* hypernymic relation “stubs” *}

3: for term t ∈ c do

4: if t ∈ R then

5: h ← hyper(t, R,t

)

6: H ← H ∪ h

7: end if

8: end for

9: annotate all terms in c with the hypernyms from the set H

10: end for

11: return onto(C)

Algorithm 2 Empirical reﬁnement.

1: process the resources by the pattern-based method and produce a set of

ontologies S

2: merge the ontologies in S

into one ontology R

3: process the resources by the clustering-based method (Alg. 1 and Alg. 2)

using R as a reference ontology in Alg. 2 and produce set of ontologies

4: merge the ontologies in S

and produce ontology C

5: join the R and C in order to produce domain taxonomy in ontology D

6: return D

Algorithm 3 Simpliﬁed rough clustering.

Require: V — set of feature-vectors mapped to respective terms

Require: k — number of desired clusters

Require: r — number of optimisation repeats, value 5 was found to be suf-

ﬁcient

Require: centroid(V) — function that computes centroid of the vector set

Require: dist(u, v) — cosine distance of two vectors u,v

Require: pickBal(d

,V) — abstract (due to simplicity of the description)

function, which pops a subset S from set V; S is characterised by these

conditions: (1) all v ∈ S all the closest possible vectors to d

, and (2) all

the sets picked fromV are balanced in size after a sequence of pickBal()

applications that makes V empty

1: M

init

← random v ∈ V {* initial means *}

2: V

tmp

← V

3: repeat

4: c ← centroid(M

init

)

5: v ← u such that dist(u,c) is maximal for u ∈ V

tmp

6: M

init

← M

init

∪ {v}

7: V

tmp

← V

tmp

− {v}

8: until |M

init

| < k

9: FACT ← {} {* empty map *}

10: V

tmp

← V

11: j ← 0

12: for d

∈ M

init

13: S

balanced

← pickBal(d

tmp

)

14: j ← j + 1

15: FACT[ j] ← S

balanced

16: end for

17: C ←

18: for j ∈ FACT.keys() do

19: C ← C ∪ centroid(FACT[ j])

20: end for

21: VECT2SCORE ← {} {* empty map *}

22: for v ∈ V do

23: VECT2SCORE[v] ← {(c

, 0), . . . , (c

k−1

, k − 1)} such that

, . . . , c

k−1

} is a sequence of centroids from C ordered by the

increasing distance from v

24: end for

25: CLUST ←

0 {* clustering structure *}

26: S ← {} {* empty map *}

27: for j ∈ {1, . . . , r} do

28: S

tmp

← random shufﬂe of V

29: initialize clustering c

with clusters given by pivotal centroids from

30: sequentially process S

tmp

and assign each vector to the nearest avail-

able cluster from c

, keeping the clusters as balanced in size as pos-

sible

31: compute the score S[j] for the obtained clustering by summing up

the numbers pointed by respective centroids in VECT2SCORE for

each vector in each cluster in c

32: CLUST ← CLUST ∪ c

33: end for

34: return c

∈ CLUST with lowest score S[ j], s ∈ {1, . . . , r} associated

ICEIS 2007 - International Conference on Enterprise Information Systems