MATRIX BASED PROBLEM DETECTION IN THE APPLICATION

OF SOFTWARE PROCESS PATTERNS

Chintan Amrit and Jos Van Hillegersberg

Department of IS & CM, University of Twente, Enschede, The Netherlands

Keywords:

Software Engineering, Social Factors, Process Patterns.

Abstract:

Software development is rarely an individual effort and generally involves teams of developers. Such col-

laborations require proper communication and regular coordination among the team members. In addition,

coordination is required to sort out problems due to technical dependencies that exist when components of one

part of the architecture requires service s or data input from components of another part of the architecture. The

dynamic allocation of the different tasks to people results in various socio-technical structure clashes (STSCs).

These STSCs become more pronounced in an Agile Software Development environment and managerial in-

tervention is constantly required to alleviate problems due to STSCs. In this paper we propose a technique

based on dependency matrices that detects STSCs in the organizational process structure. We illustrate this

technique using two examples from Organizational and Process Pattern literature.

1 INTRODUCTION

While there are many ways to describe a patterns,

Christopher Alexander who originated the notion of

patterns in the ﬁeld of building architecture described

patterns as a recurring solution to a common prob-

lem in a given context and system of forces (Alexan-

der et al., 1977). In Software Engineering patterns

are attempts to describe successful solutions to com-

mon software problems (Schmidt et al., 1996). Soft-

ware Patterns reﬂect common conceptual structures

of these solutions and can be used repeatedly when

analyzing, designing and producing applications in a

particular context. Patterns represent the knowledge

and experience that underlie many redesign and re-

engineering efforts of developers who have struggled

to achieve greater reuse and ﬂexibility of their soft-

ware. The different types of patterns are:

• Design Patterns: Are simple and elegant solu-

tions to speciﬁc problems in object oriented de-

sign (Gamma et al., 1995).

• Analysis Patterns: Capture conceptual models in

an application domain in order to allow reuse

across applications (Fowler, 1997).

• Organizational Patterns: Describe the structure

and practices of human organizations (Coplien

and Harrison, 2004).

• Process Patterns: Describe the Software Design

Process (Coplien and Schmidt, 1995).

Patterns are most generally represented in natu-

ral language and are typically published in printed

catalogues. Pattern presentation is generally loosely

structured and consists of a series of ﬁelds each hav-

ing a meaning introduced via an informal deﬁnition

or description. An example of such a structure repre-

senting patterns can be found in (Gamma et al., 1995).

Identifying the problem areas related to process

patterns (Coplien and Schmidt, 1995; Coplien and

Harrison, 2004) (which we would refer to as Socio-

Technical Structure Clashes or STSC henceforth)

can prove difﬁcult for large distributed or collocated

teams working on large software projects. The rea-

son why the patterns are hard to implement is that the

problems, or STSCs in our case addressed by the pat-

terns are hard to detect, as purely manual techniques

are labour intensive. We contend that by automating

the process of STSC detection we can help monitor

a large software development process. Process moni-

316

Amrit C. and Van Hillegersberg J. (2007).

MATRIX BASED PROBLEM DETECTION IN THE APPLICATION OF SOFTWARE PROCESS PATTERNS.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - ISAS, pages 316-320

DOI: 10.5220/0002395503160320

 SciTePress

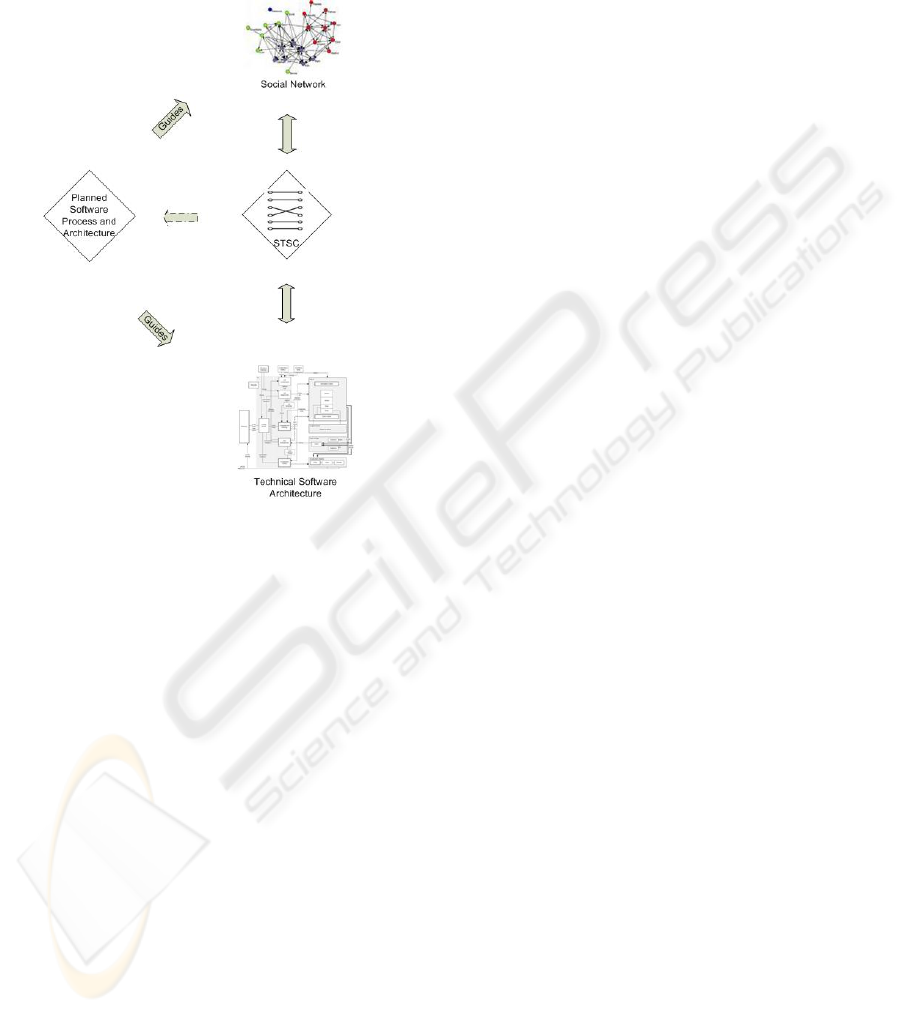
toring becomes essential in such an agile environment

in order to keep the development process in check.

Detection of such STSCs can help in reengineering

the informal design process model in order to improve

project planning (Fig. 1).

Figure 1: Planned Software Process refactoring using

Socio-Technical Structure Clashes.

One needs a proper formalism of STSC in order

to automate the process of problem detection and then

leave it the manager’s discretion, whether the particu-

lar pattern has to be applied. However, there has been

little research done in the area of formalisms of such

problem scenarios (STSCs).

In this paper we propose a technique that detects

STSCs and a metric to gauge the extent of the STSC.

In order to illustrate this technique we apply it to

two patterns related to software development in dis-

tributed or collocated teams.

The rest of the paper is organized as follows; Section

2 describes the construction process of the process de-

pendency matrices, Section 3 describes the matrix for-

mulation with the developing in pair’s pattern, Section

4 describes the matrix formulation with the Conway’s

law pattern and concluding remarks are given in Sec-

tion 5.

2 CONSTRUCTION OF THE

PROCESS DEPENDENCY

MATRICES

Dependency matrices have been used in Engineering

literature to represent the dependency between peo-

ple and tasks (Steven et al., 1994). Recent empirical

work uses DSMs to provide critical insights into the

relationship between product architecture and orga-

nizational structure. For example, Sosa et al (Sosa

et al., 2004) ﬁnd a strong tendency for design interac-

tions and team interactions to be aligned, and show

instances of misalignment are more likely to occur

across organizational and system boundaries. Li et

al. (Li et al., 2005) use dependency matrices to an-

alyze dependencies between components in a CBS

(Component Based System). Sullivan et al (Sullivan

et al., 2001) use DSMs to formally model (and value)

the concept of information hiding, the principle pro-

posed by Parnas to divide designs into modules (Par-

nas, 1972). Here we create what we call process de-

pendency matrices in order to represent the connec-

tions between software modules, software develop-

ers as well as the modules each developer is working

on. Only the modiﬁed modules are considered at any

point of time, as these are the modules which require

communication to resolve dependency issues, espe-

cially in an agile environment (Wagstrom and Herb-

sleb, 2006; Cataldo et al., 2006). In the notation used

here A[i, j] represents a matrix, while a

i j

represents

the (i, j)

element of the matrix. From the CVS (Con-

current Versioning System) we can obtain two kinds

of adjacency matrices. One is the m ∗ m adjacency

matrix SM[i, j] representing the software dependency

graph of the modiﬁed modules (Myers, 2003)(assum-

ing there are m modules) and the other an m ∗ n adja-

cency matrix SMA[i, j] representing the allocation of

modules to the developers (assuming there are n de-

velopers working on the m modules). The software

dependency matrix would represent:

• Function call dependency

• Inheritance dependency

• Aggregation dependency

The software dependency matrix would appear as:

SM[i, j] =







· · · sm







Which can be concisely represented as:

MATRIX BASED PROBLEM DETECTION IN THE APPLICATION OF SOFTWARE PROCESS PATTERNS

317

(sm

i j

) =



1 i f c

→ c

;

0 otherwise

Where c

are software modules, whereas each sm

i j

represents the relation between the modules as de-

scribed above. Similarly, the n ∗ m Software Module

Allocation adjacency matrix would appear as:

SMA[i, j ] =







sma

· · · sma

sma

· · · sma

sma

· · · sma







Where the rows represent the software developers

working on modules which are represented along the

columns. This matrix can be concisely represented as:

(sma

i j

) =



1 i f sd

→ c

;

0 otherwise

Where each sd

represents a software developer, while

each c

represents a software module. Hence, we see

that each sma

i j

represents the relation between them,

which is, in this case, whether the particular developer

is developing the module c

in question. The sym-

metric n∗n matrix SND[i, j] representing the work re-

lated communication network of the developers can

be represented as:

(snd

i j

) =



1 i f sd

→ sd

;

0 otherwise

That is each element snd

i j

of the matrix SND[i, j] has

a value of 1 if the i

person is talking to the j

person,

where each row of the SND[i, j] matrix corresponds

to the same developers as the rows of the SMA[i, j]

matrix. We now utilize these matrices in order to de-

scribe the problem scenarios of two process patterns.

3 DEVELOPING IN PAIR’S

PATTERN

This pattern deals with pairing compatible program-

mers together so that they can produce more to-

gether than they can working individually (Coplien

and Schmidt, 1995). Also there has been research

claiming that pair programming produces better prod-

ucts in less time (Williams et al., 2000). Further, it

is better for the software product when all its mod-

ules has two developers working on it, as when one

of them leaves the company the other has an idea of

what is to be done.

In our matrix based technique, we create a n ∗ t ma-

trix (PP[i, j]) which has all the software modules in

the matrix (SMA[i, j]) developed by at the most one

programmer. Hence, if t = 0 then it means all the

software modules are developed by two or more pro-

grammers. The matrix (PP[i, j]) gives an indication

of the possible problematic software modules; those

with only one programmer working on it as well as

those with no one currently responsible. We can ex-

press the (PP[i, j]) matrix as in eq (1).

(pp

i j

) =

sma

i j

,i f f

∑

k=1

sma

k j

< 2, ∀1 ≤ j ≤ m,1 ≤ i ≤ n

(1)

4 CONWAYS LAW PATTERN

”Organizations which design systems (...) are con-

strained to produce designs which are copies of

the communication structures of these organizations”

(Conway, 1968)

This pattern states that the structure of the system mir-

rors the structure of the organization that designed it.

The shaping forces behind this law are that, architec-

ture shapes the communication paths in an organiza-

tion and that formal organization structure shapes ar-

chitecture (Coplien and Schmidt, 1995; Herbsleb and

Grinter, 1999). Another way of looking at Conway’s

law is saying that dependencies between software

modules cause dependencies between the develop-

ers developing them. The dependencies between the

code modules maybe inheritance, aggregation or sim-

ple function calls from one module to another. These

dependencies create further dependencies among the

programmers who work on the particular modules

(Conway, 1968).

We use adjacency matrices to suggest a depen-

dency metric which can be used to measure depen-

dencies in allocations of software modules.

4.1 Conways Law Dependency Matrix

Construction

For the sake of this research we consider two kinds of

dependencies in the development of software:

1. Developers working on the same modules.

2. Developers working on modules which are mutu-

ally dependent themselves.

We propose an algorithm for the construction of

a n ∗ n adjacency matrix representing the dependency

ICEIS 2007 - International Conference on Enterprise Information Systems

318

between Software Developers based on eq (2).

(sdd

i j

) =











1 i f sma

∧ sma

= 1,

∀1 ≤ k ≤ m;

1 i f sma

∧ sma

∧ sm

= 1,

∀1 ≤ k ≤ m,1 ≤ l ≤ m;

0 otherwise

(2)

In the above construction of the software devel-

oper dependency matrix, the value of 1 is assigned

whenever there are more than one developer working

on the same software module. Also a 1 is assigned

whenever developers work on modules which share a

dependency.

The logical difference between the software de-

veloper dependency matrix (SDD[i, j]) and the ma-

trix representing the work related communication net-

work of the software developers (SND[i, j]) would

give us a n∗ n matrix (DDM[i, j]) which represents the

unresolved dependencies in the existing communica-

tion network of developers. This can be represented

as in eq (3).

(ddm

i j

) =



sdd

i j

∧ snd

i j



(3)

The summation of the logical difference between

the software developer dependency matrix (SDD[i, j])

and the matrix representing the work related social

network of the software developers (SND[i, j]) would

give us a metric which suggests the requirement of

greater communication among the software develop-

ers. As we are only considering undirected networks

the matrices (SDD[i, j]) and (SND[i, j]) are symmetri-

cal. So, the summation should be divided by 2 to get

the actual number of non-existent dependencies. This

can be described as a dependency metric as in eq (4).

depdendency metric = 1/2

∑

i=1, j=1

(sdd

i j

∧ snd

i j

)

(4)

Using these two matrices we construct the depen-

dency matrix of the developers using the following

algorithm:

To calculate the transitive dependencies we can

use Warshall’s algorithm (Warshall, 1962) (see

Appendix) for transitive closure of the matrix

(SDD[i, j]).

5 SPECIFYING PATTERN

SOLUTIONS

5.1 Gatekeeper Pattern

The Gatekeeper pattern (Pattern No. 23 (Coplien,

1994)) basically says that one needs to balance

communication with typically introverted engineer-

ing types. This role implies that the person dissemi-

nates leading and fringe information from outside the

project to project members. This role of being a Gate

Keeper is similar to being a coordinating member of

the team. The measure of the degree to which a team

member is a Gate Keeper is similar to measuring the

coordination ability of the person (Scott, 2000). Be-

tweenness refers to the frequency with which a node

falls between pairs of other nodes in the network.

6 CONCLUSION

In this paper we propose a technique for formal-

izing problems related to Socio-Technical Structure

Clashes or STSCs in organizations. Once these

STSCs have been identiﬁed, we can leave it to the

discretion of the responsible manager to apply the par-

ticular process pattern related to the problem in hand.

We have demonstrated this technique with two partic-

ular problems related to assignment of software mod-

ules to developers. The ﬁrst STSC is related to pair

programming, where there might be no developer or

just one developer involved in developing what might

be an important software module. If this particular

developer leaves the company then there could be de-

lays and unwanted associated costs.

The second STSC deals with dependencies in soft-

ware modules which create an intrinsic dependency

between programmers working on it. The assumption

in this STSC is that all the dependencies between soft-

ware modules incur the same cost. We could also use

the concept of Clustered Cost (MacCormack et al.,

ming) in order to attribute a different cost to the de-

pendency between developers due to modules that are

more closely clustered as compared to other modules.

Though past research in CSCW has focussed on these

dependencies (de Souza et al., 2004), they haven’t de-

scribed any technique to effectively identify the prob-

lem that they are trying to solve. We have described

a technique to identify these dependencies, as well

as a metric to calculate to measure the extent of the

problem, before trying to resolve the dependencies.

This dependency metric varies with time, as do all the

matrices represented. We could also plot this metric

and its changes with time to get a better idea of how

the project evolves. We have developed a tool called

PatoNet which implements some the algorithms de-

scribed in this paper. Future work could involve for-

malizing the problem structure of other process pat-

terns and thereby enabling an easier pattern applica-

tion.

MATRIX BASED PROBLEM DETECTION IN THE APPLICATION OF SOFTWARE PROCESS PATTERNS

319

REFERENCES

Alexander, C., Ishikawa, S., and Silverstein, L. A. (1977).

A Pattern Language. Oxford University Press, New

York.

Cataldo, M., Wagstrom, P. A., Herbsleb, J. D., and Car-

ley, K. M. (2006). Identiﬁcation of coordination re-

quirements: implications for the design of collabora-

tion and awareness tools. In CSCW ’06: Proceed-

ings of the 2006 20th anniversary conferen ce on Com-

puter supported cooperative work, pages 353–362,

New York, NY, USA. ACM Press.

Conway, M. (1968). How do committees invent. Datama-

tion, 14:28–31.

Coplien, J. O. and Schmidt, D. C. (1995). Pattern languages

of program design. ACM Press/Addison-Wesley Pub-

lishing Co., New York, NY, USA.

Coplien, James, O. (1994). A development process genera-

tive pattern language. pages 1–33.

Coplien, James, O. and Harrison, Neil, B. (2004). Or-

ganizational Patterns of Agile Software Development.

Prentice-Hall, Inc., Upper Saddle River, NJ, USA.

de Souza, Cleidson, R. B., Redmiles, D., Cheng, L.-T.,

Millen, D., and Patterson, J. (2004). Sometimes you

need to see through walls: a ﬁeld study of application

programming interfaces. In CSCW ’04: Proceedings

of the 2004 ACM conference on Computer supported

cooperative work, pages 63–71, New York, NY, USA.

ACM Press.

Fowler, M. (1997). Analysis Patterns: Reusable Object

Models. Addison Wesley, Reading MA.

Gamma, E., Helm, R., Johnson, R., and Vlissides, J. (1995).

Design Patterns: Elements of Resuable Object Ori-

ented Software. Addison Wesley, MA.

Herbsleb, James, D. and Grinter, Rebecca, E. (1999). Ar-

chitectures, coordination, and distance: Conway’s law

and beyond. IEEE Softw., 16(5):63–70.

Li, B., Zhou, Y., Wang, Y., and Mo, J. (2005). Matrix-

based component dependence representation and its

applications in software quality assurance. SIGPLAN

Not., 40(11):29–36.

MacCormack, A., Rusnak, J., and Baldwin, C. (forthcom-

ing). Exploring the structure of complex software de-

signs: An empirical study of open source and propri-

etary code. Management Science.

Myers, Christopher, R. (2003). Software systems as com-

plex networks: Structure, function, and evolvability

of software collaboration graphs. Physical Review

E (Statistical, Nonlinear, and Soft Matter Physics),

68(4):046116.

Parnas, D. L. (1972). On the criteria to be used in de-

composing systems into modules. Commun. ACM,

15(12):1053–1058.

Schmidt, D., Fayad, M., and Johnson, R. E. (1996). Soft-

ware patterns. Communication of the ACM, 39:37–39.

Scott, J. (2000). Social Network Analysis: a handbook.

Sage Publications Inc.

Sosa, M. E., Eppinger, S. D., and Rowles, C. M. (2004).

The misalignment of product architecture and organi-

zational structure in complex product development. J

Manage. Sci., 50(12):1674–1689.

Steven, D. E., Daniel, E. W., Robert, P. S., and David, A. G.

(1994). A model-based method for organizing tasks

in product development. Research in Engineering De-

sign, V6(1):1–13. 10.1007/BF01588087.

Sullivan, K. J., Griswold, W. G., Cai, Y., and Hallen, B.

(2001). The structure and value of modularity in soft-

ware design. In ESEC/FSE-9: Proceedings of the

8th European software engineering conference held

jointly with 9th ACM SIGSOFT international sympo-

sium on Foundations of software engineering, pages

99–108, New York, NY, USA. ACM Press.

Wagstrom, P. and Herbsleb, James, D. (2006). Dependency

forecasting in the distributed agile organization. Com-

mun. ACM, 49(10):55–56.

Warshall, S. (1962). A theorem on boolean matrices. J.

ACM, 9(1):11–12.

Williams, L., Kessler, Robert, R., Cunningham, W., and Jef-

fries, R. (2000). Strengthening the case for pair pro-

gramming. IEEE Softw., 17(4):19–25.

APPENDIX

WARSHALL’S ALGORITHM

Warshalls Algorithm of transitive closure. Given di-

rected graph G = (V,E), represented by an adjacency

matrix A[i, j], where A[i, j] = 1 if (i, j) is in E, com-

pute the matrix P, where P[i, j] is 1 if there is a length

greater than or equal to 1 from i to j.

Warshall(int N, bool[1..n,1..n] A, bool[1..n,1..n] P)

{

int i,j,k;

for(i=0; i<N;i++)

for(j=0; j<N; j++)

P[i,j]=A[i,j]

for(k=0; k<N; k++)

for(i=0;i<N; i++)

for(j=0; j<N; j++)

if(!P[i,j]) P[i,j]=P[i,k]&&P[k,j];

}

ICEIS 2007 - International Conference on Enterprise Information Systems

320