
RULE BASED STABILITY CRITERIA FOR COALITION
FORMATION UNDER UNCERTAINTY
Chi-Kong Chan and Ho-Fung Leung
Department of Computer Science and Engineering
The Chinese University of Hong Kong
Hong Kong
Keywords:
Coalition Formation, Stability, Uncertainty.
Abstract:
Efficiency and stability are two important concepts in coalition formation analysis. One common assumption
in many well-known criteria such as the core and Pareto- efficiency is that there exists a publicly known value
for each coalition or sub-coalition. However, in software agent applications, this assumption is often not true as
the agents rarely know the exact coalition values for certain. Instead, agents have to rely on whatever evidence
they can observe, and evaluate those evidence according to their private information base on past experience.
There are two sources of uncertainty here. First, such private information is often uncertain in nature or may
even be self-conflicting. Second, the agents, which are heterogeneous and autonomous, may have different
conflict resolution strategies. Such uncertainties make the traditional approaches unfit for many real-world
problems, except perhaps, in idealized scenarios. In this paper, we extend the core and Pareto optimality
criteria by proposing a new rule based stability concepts under uncertain environment: the CU-Core.
1 INTRODUCTION
Cooperation is one important feature of multi-agents
systems. For example, agents in a semi-competitive
environment often need to form coalitions in order to
achieve tasks that cannot be done alone, or to maxi-
mize their own payoff via mutually benefiting agree-
ments. Many coalition formation mechanisms have
been proposed in the past (Blankenburg and Klusch,
2004; Sandholm, 1999; Ketchpel, 1994). In order to
analyze the stability and efficiency of such coalitional
games, many models have been developed, especially
in cooperative game theory (Osborne and Rubinstein,
1994; Scarf, 1967).
In a coalitional game, each coalition is associated
with a set of feasible allocations or consequences,
which are the outcome of the game as a result of the
agents’ joint action. One classic solution concept in
cooperative game theory is the core (Gillies, 1959;
Osborne and Rubinstein, 1994), which defines that a
certain allocation for a coalition is stable (i.e, in the
core) if no individual members or groups of mem-
bers can deviate from the original coalition and ob-
tain a more preferable outcome for each of the devi-
ating members. The core either requires the specifi-
cation of publicly known values of each possible allo-
cation for all coalition and sub-coalitions, or, in non-
transferable utility games, the agents’ preferences re-
garding each possible consequences obtainable by the
coalition. In both cases, the values or the preferences
are supposed to be known for certain.
In many software agent problems, we are not able
to attach such an exact value or preferences for ev-
ery coalitional game that we analyze, as there are of-
ten uncertainties regarding the achievable outcomes
of a coalition: two agents cooperating to solve a cer-
tain task may not know for certain whether their plan
will be successful or not; an agent’s preference may
depend on the future value of some unknown envi-
ronment parameters. However, such uncertainty does
not defer coalitions to be formed in the real world.
Instead of evaluating a proposed coalition by pre-
defined preferences or publicly known values as done
in traditional approaches, agents tend to rely on vari-
ous available information from their previous experi-
ence to predict the future outcome, based on whatever
information they can currently observe.
As an example, consider a buyer coalition prob-
lem (Yamamoto and Sycara, 2001; He and Ioerger,
2004) where several agents are negotiating to form
coalitions to buy items of good quality from some on-
line sellers (for example, they may form groups in or-
der to obtain volume discounts). Typically, the only
observable attributes regarding an item being sold on-
171
Chan C. and Leung H. (2007).
RULE BASED STABILITY CRITERIA FOR COALITION FORMATION UNDER UNCERTAINTY.
In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 171-177
DOI: 10.5220/0002397401710177
Copyright
c
SciTePress

line is the item’s product name, brand-name, item’s
location and the seller’s name, whereas the quality of
the item is not observable (or not verifiable) at the
time of purchase. One thing that the agents can do
in this uncertain situation is to match those attribute
values against the quality of other items in their pre-
vious purchase experience. For example, the buyer
may want to consider the quality of previously bought
items from the same brand and the same seller. This
way, each agent can have an estimation of the qual-
ity of the current item, which in turn influences the
agent’s decision of whether to join the buyer coalition
or not. Thus, to each agent, the problem now becomes
a series of classification problems: given the observ-
able item attributes, an agent must classify each pos-
sible coalition as either “preferred” or “not preferred”
where “preferred” means that the agents believe there
is no better options. From this point of view, such a
coalition is stable if only if every member of the coali-
tion “prefers” it.
Several extensions of the core have been proposed
in order to model coalitional games with uncertainty,
for instance, a stochastic payoff approach is proposed
in (Suijs et al., 1999) and a Bayesian core proposed in
(Chalkiadakis and Boutilier, 2004). However, while
these works provide good theoretical foundation on
stochastic cooperative games, they are not suitable to
handle problems such as the buyer coalition game de-
scribed above, as the samples (i.e., the agent’s pur-
chase experience) are often too sparse to provide
any meaningful estimation of the probability distri-
butions, which these approaches rely on. So instead,
we are taking a rule based approach. In this approach,
each agent is assumed to hava some private knowl-
edge which can be used to generate rules. However,
private knowledge are not always without uncertainty
(for example, two similar items in the buying his-
tory may have different quality), resulting in rules that
may conflict with each other. Thus the stability of a
coalition game depends not only on the observable at-
tributes and the decision rules of each agent, but also
on how such conflicts are resolved by each agent.
Because of this, we argue that it is not sufficient
to describe such coalitions as simply ”stable” (i.e,
in the core) or not, as done in the core-based ap-
proaches. Instead, we propose a new stability crite-
ria, the CU-core. The CU-core divides the obtain-
able consequences of a coalition into three stabil-
ity classes: those that are certainly stable (c-core),
those that may be stable (u-core), depending on the
agents’ conflict resolution strategies, and those that
are certainly not stable. We believe the proposed con-
cepts can provide useful solution concepts for this
emerging type of coalition games, which we call non-
Table 1: Preference of agents in Example 1.
A
1
A
2
A
3
A
4
Good Movie Movie Movie Movie
Average Movie Movie Tennis Tennis
Bad Tennis Tennis Tennis Tennis
transferable utility games with uncertainty.
The remaining of this paper is organized as fol-
lows. Section 2 illustrates the main ideas by dis-
cussing a coalition formation problem that is not well
handled by the traditional core-based approaches.
Section 3 discusses some related background con-
cepts. Section 4 defines a type of game which we la-
beled non-transferable utility game with uncertainty.
A rule based agent decision model is defined in sec-
tion 5. Section 6 defines the new stability concepts
of CU-core. Some potential applications of the pro-
posed concepts are discussed in section 7. Section 8
lists some related works. After that, we conclude.
2 AN MOTIVATING EXAMPLE
In this section we study an example that cannot be
handled by the core-based approaches.
Example 1. Four agents A
1
to A
4
are planning to do
one of two possible activities: they either go to play
tennis or they go to watch a science fiction (S.F.)
movie produced by a director named Steven Spiel-
berg. Suppose the preference of each agent depends
on one factor only, the quality of the movie, which
can either be good, average or bad. Their exact pref-
erences are described in table 1. If the movie is good,
then all four agents prefer the movie over tennis. On
the contrary, if the movie is bad, then all four agents
prefer tennis over movie. However, if the quality is
average, then A
1
and A
2
prefer the movie, but A
3
and
A
4
prefer to play tennis instead. Also, assuming all
else being equal, the agents prefer to attend an activity
in a group (i.e., coalition) that is as large as possible.
For example, a tennis coalition of four agents is pre-
ferred over two tennis coalitions of two tennis players
each. We also assume that all agents in the same coali-
tion perform the same activity, and that should any
agents decide to play tennis, they must go in groups
of even number of players.
There are difficulties in analyzing this game us-
ing the traditional core based approaches. First, it is
not possible to assign a transferable coalition value to
each possible allocation or consequence of each sub-
coalition: while the agents know their preferences in
ICEIS 2007 - International Conference on Enterprise Information Systems
172
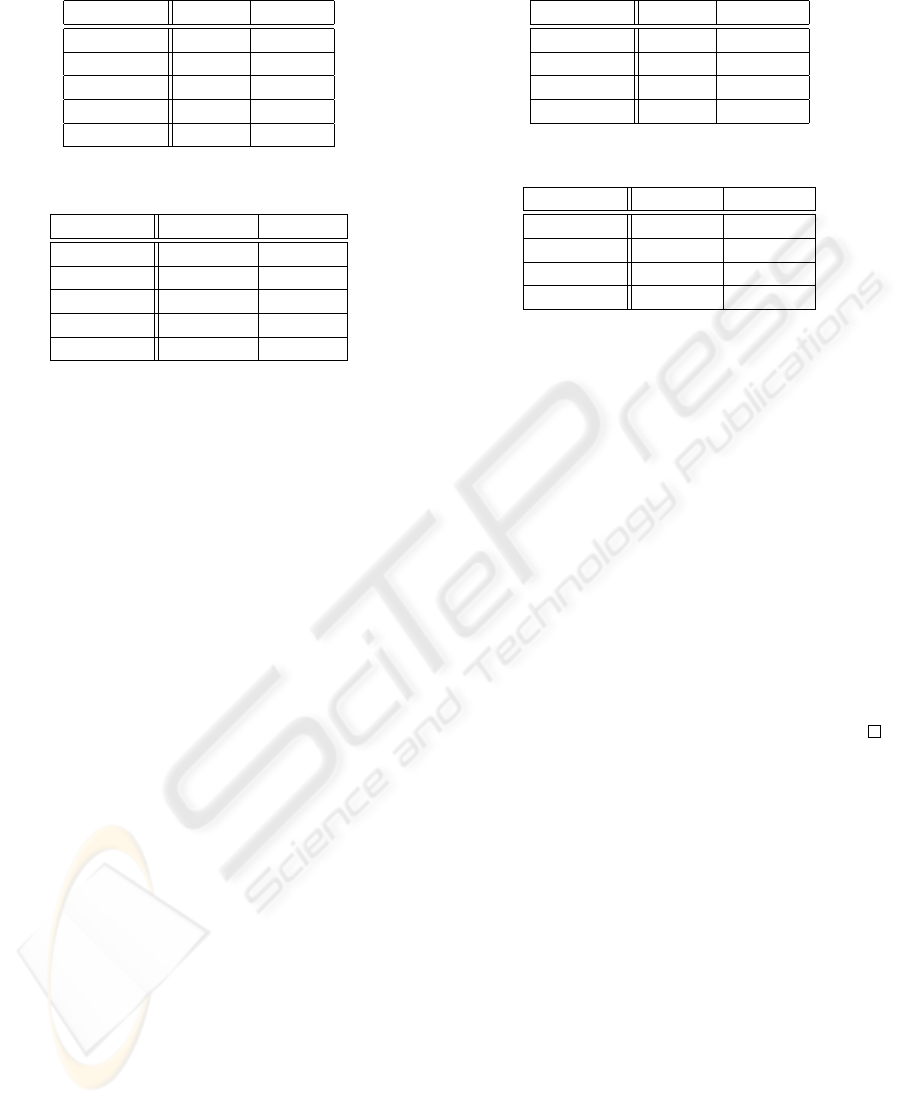
Table 2: Decision table of A
1
.
Director Type Quality
Spielberg S.F. Good
Spielberg Drama Good
Spielberg S.F. Good
Copploa Drama Good
Tempa Action Bad
Table 3: Decision table of A
2
.
Director Type Quality
Spielberg S.F. Good
Spielberg S.F. Good
Lau Crime Good
Tempa Comedy Bad
Cameron Romance Average
each of the three possible quality-dependent scenar-
ios, little is known about the exact private value (or
utility) that each agent places on each outcome.
But the main problem here is that even those pref-
erences are uncertain and depend on the quality of
the movie, which is unknown at the time of negoti-
ation. Now, suppose that the agents keep records of
the movies they have seen before as shown in table
2 to table 5. Each table records the director, movie
type and quality of the movies of an agent’s viewing
history and the agent uses it to predict the quality of
current movie. For example, agent A
1
will have the
opinion that the current movie (an S.F. movie directed
by Spielberg) will probably be good since the quali-
ties of all similar cases in his experience (table 2) are
good.
However, even with such extra information, it is
still hard to apply the traditional core-based game
analysis to this game because the outcome will still
depend on how the experiences are interpreted by the
individual agents.
Let us first consider a two agents movie coalition
{A
1
, A
2
}. This case is straightforward enough: both
agents will have the opinion that the movie should be
good, since the qualities of all previous Spielberg’s
S.F. movies in their experience have been good, and,
according to their preference in table 1, movie is pre-
ferred over tennis in this case. So if both agents make
their decision purely based on their experience, the
coalition would certainly be stable. Similarly, any
tennis coalition involving either A
1
or A
2
will cer-
tainly fall apart as both agents have a better option.
However, a {A
1
, A
2
, A
3
, A
4
} movie coalition is
more problematic as there are conflicting entries in
the viewing history of A
3
and A
4
. In this case, both A
3
Table 4: Decision table of A
3
.
Director Type Quality
Spielberg S.F. Average
Spielberg S.F. Good
Lucas S.F. Good
King Drama Bad
Table 5: Decision table of A
4
.
Director Type Quality
Spielberg S.F. Good
Spielberg S.F. Average
King Comedy Average
Mora Action Bad
and A
4
can only conclude from their experience that
the quality of the current movie may either be “good”
or “average”, yet according to their preference, both
agents will stay in the coalition only if the quality is
good. Therefore the stability of this coalition depends
on how the conflicts are resolved by the two agents.
Thus we see that the traditional core-based coali-
tion stability concepts, which classify all solutions as
either being in the core or not, are insufficient to de-
scribe games such as this one. Instead, we need a new
model that can classify coalitions into different lev-
els of stability. On one extreme, we have the certainly
stable coalitions such as the {A
1
, A
2
} movie coalition.
On the other extreme, we have the certainly not stable
coalition of {A
1
, A
2
} tennis coalition, and somewhere
in between, we have the conditionally stable movie
coalition of {A
1
, A
2
, A
3
, A
4
}.
The game discussed in Example 1 is a type of
game called non-transferable utility games with un-
certainty (NTUU games). Yet, to our knowledge,
there are currently few coalition formation algorithms
proposed for such type of games. One reason for
that could be the current lack of useful solution con-
cepts. As mentioned above, the probabilistic based
solution concepts are unsuitable for this type of games
for two reasons. First, these existing works focus
mainly on games with transferable utilities. Second,
there are cases where a probabilistic model is not suit-
able, such as multi-agent cooperation games where
the samples (agent’s experience) are too sparse to pro-
vide any meaningful estimation of the probability dis-
tributions (as seen in Example 1), or in applications
where the agents employ rule-based reasoning and
where knowledge is kept in form of decision rules or
in decision tables, which is the case in many A.I. sys-
tems. For these reasons, we are proposing a new so-
lution concepts that is suitable for NTUU games in
RULE BASED STABILITY CRITERIA FOR COALITION FORMATION UNDER UNCERTAINTY
173

general, and we believe the model can fill a gap in the
current approaches.
3 BACKGROUND: NTU GAMES
A coalition game with non-transferable utility (NTU
games) can be described as follows. A set of agents
N = {1,. . . , n} is called a coalition, and each sub-
set S ⊆ N is called a sub-coalition. Each coalition
and sub-coalition is associated with a set of feasible
consequences, which are the possible outcomes that
can be achieved as a result of some joint-action of
the members of that coalition (or sub-coalition). For
example, the consequence of a buyer coalition game
may be the number of goods received by each member
of the sub-coalition and the amount they pay, whereas
the set of feasible consequences are those that con-
form to the selling price of the items. Each agent
has a preference relation on the set of feasible con-
sequences such that for any two feasible consequence
x
1
and x
2
, we have x
1
i
x
2
iff x
1
is no less preferred
than x
2
to that agent i.
More formally, we can define an NTU game by
a tuple g =< N, X,V,(
i
) >, where, N = {1, . . . , n}
is the set of agents (a coalition). X is the set of con-
sequences. V : 2
N
→ 2
X
is a function that map each
sub-coalition S ⊆ N to a set of feasible consequence
V(S) ⊆ X.
i
is the i-th agent’s preference relation.
The core of an NTU game is then defined as the
set of consequences such that no sub-coalition S ⊆
N can defect by finding an alternative consequence
where each member of the sub-coalition S would pre-
fer the alternative consequence. That is, a conse-
quence x ∈ V(N) is in the core if there does not exist
a sub-coalition S ⊆ N and an alternative consequence
y ∈ V(N) such that y
i
x∀ i ∈ S.
4 NTU GAMES WITH
UNCERTAINTY
Traditional game theory concepts such as NTU games
and the core are insufficient in modeling the game in
Example 1. The reason is that we are actually facing a
new type of game where the outcome is uncertain. We
call this new type of game Non-transferable Utility
Games with Uncertainty (NTUU games).
We propose a model for this type of games as
illustrated in figure 1. An NTUU game is defined
by a tuple g =< N, E, (I
i
), H, X, (P
i
) > as follows.
N = {1, . . . n} is the set of agents, which is called a
coalition. X is a set of feasible consequences, i.e., out-
Agent n
Preference
Experience
Preferences
Observable Attributes (Evidence)
Preference
Experience
Agent 1
Hidden Attribute
(The state)
Environment Attributes
. . .
XFeasible Consequence
PRules
BOpinions
IRules
PRules
BOpinions
Rules I
E
Preferences
CU-CORE
Figure 1: Non-transferable utility game with uncertainty.
comes that can be achieved as a result of some joint-
action of the members of that coalition. E = {(a
1
=
v
1
) ∧ (a
2
= v
2
) ∧ ··· ∧ (a
k
= v
k
)} is the evidence that
are observable by each agent, where each a
i
is the
name of an observable environmental attribute and v
i
its current value. H is a currently non-observable at-
tribute called the state, with V
H
being its allowed set
of values. Without loss of generality, we can always
assume there is only one non-observable attribute. (If
there are more than one such attributes, we can simple
define the state to be a tuple of the hidden attributes).
The state is the attribute that affects the agents prefer-
ence. (I
i
) is the i-th agents’ experiences, where each
I
i
= (I
1
i
, I
2
i
, . . . , I
r
i
) is a collection of the agents experi-
ence rules. Each experience rule I
j
i
is of the form
(a
1
= v
1
) ∧ (a
2
= v
2
) ∧ ··· ∧ (a
k
= v
k
) ⇒ d
r
where each a
i
corresponds to the name of an environ-
mental variable and v
i
its value, d
r
∈ V
H
corresponds
to a value of the state. Each rule represents one in-
stance of an agent’s previous experience in dealing
with problems similar to the current one. P
i
is the i-th
agent’s set of preference rules. Each preference rule
has the form:
{d
1
, d
2
, . . . , d
m
} ⇒ x ≻
i
x
′
where d
i
∈ V
H
denotes a possible value of the state,
and x and x
′
are feasible consequences.
As an example, consider the game in Exam-
ple 1, where four agents are discussing to form
coalitions to either see a Spielberg’s S.F movie
or to play tennis. It can be modeled as follows:
in this example, we have N = {A
1
, A
2
, A
3
, A
4
}
being the set of agents. Some of the feasible
consequence X for this coalition are
(tennis,
tennis, tennis, tennis), (tennis, tennis,
ICEIS 2007 - International Conference on Enterprise Information Systems
174

movie, movie), (movie, movie, movie,
movie)
... etc. The evidence E in this case is
{
(director=Spielberg)
∧
(type=S.F.)
}, and the
state H is the quality of the movie, whose possible
values V
H
are {
good, average, bad
}, but its value
for the current game is to be determined.
In order to estimate the value of the hidden state,
each agent is equipped some experience which is a
collection of experience rules I
i
. Here the left hand
side (L.H.S.) of the rule corresponds to a previously
observed evidence, and the right hand side (R.H.S.)
corresponds to the value of the state that occurred.
For instance, the experience of agent A
3
(table 4) can
be represented by the following experience rules:
ER1. (director = Spielberg) ∧(type = S.F.) ⇒ average
ER2. (director = Spielberg) ∧(type = S.F.) ⇒ good
ER3. (director = Lucas) ∧ (type = S.F.) ⇒ good
ER4. (director = King) ∧ (type = Drama) ⇒ bad
Note that rule ER1 and rule ER2 are in conflict
with each other. Also, any duplicating rules are re-
moved for simplicity.
We model the i-th agent’s preference by a
set of preference rules P
i
. As an example,
suppose we are given the two consequences
x
1
= (
tennis, tennis, tennis, tennis
) and
x
2
= (
movie, movie, movie, movie
), we have the
following preference rules for A
3
:
P1. {good} ⇒ x
2
≻
3
x
1
P2. {average} ⇒ x
1
≻
3
x
2
P3. {bad} ⇒ x
1
≻
3
x
2
P4. {average,bad} ⇒ x
1
≻
3
x
2
In particular, the last rule reads: “In the cases that
I (agent A
3
) have reason to believe the quality is either
average or bad but I am not sure which is the case, I
would say that x
1
is better than x
2
.”
5 OPINION AND AGENT
PREFERENCES
Before we present the CU-core, we need to discuss
two concepts: agent’s opinion and agent’s preference.
Given the evidence regarding the current game,
and a set of experience rules representing an agent’s
past experience, an agent derives its opinion as fol-
lows. The agent first matches the evidence against the
L.H.S. of the experience rules such that any matching
rules are “fired”, and the corresponding values of the
state, as suggested by the R.H.S. of the rules, become
members of the opinions of the agents. Thus, contin-
uing from the previous example, where we have evi-
dence E = {(director = Spielberg) ∧ (type = S.F)}
and the experience of agent A
3
are represented by the
rules ER1 to ER4, we see that rule ER1 and rule ER2
are fired, and the corresponding opinion of the agent
A
3
is therefore B
3
={
average, good
}. Note that this
does not intend to mean A
3
believes the probability of
any other state value other than “average” or “good”
must be zero. In most applications including our ex-
amples, the obtained samples (i.e, the agents’ experi-
ence) are far too sparse to provide any meaningful as-
sessment to the probabilistic distribution of the state
values. Rather, the opinion B
3
={
average, good
}
should be understood as “From my (i.e, agent A
3
’s)
limited (self-conflicting) experience so far, I have rea-
son to believe the state is either average or good”.
As mentioned in previous section, the preferences
of each agent are captured by a set of preference
rules. Continue from above discussion where we
have x
1
=
(tennis, tennis, tennis, tennis)
and x
2
=
(movie, movie, movie, movie)
, and the
preference rules of A
3
are the four rules P1 to P4. In
order to decide which preference rules are fired, we
first check if any of the L.H.S. of the preference rules
matches the opinion. After that, if no matching is
found, we look for partial matching that matches a
subset of the opinion. For example, given the opinion
of A
3
which is {
average, good
}, since no matching
is found, we look for partial matchings, which are P1
and P2 in this case and both rules are fired. In this
case, the preference of the agent is said to be in con-
flict as the R.H.S. of the two fired rules do not con-
tain the same value. For comparison, suppose instead
that the opinion is {
average, bad
}, then in this case,
rule P4 is fired, but not P1 and P3, as the more general
rule P4 overrides them. The reason for this is to allow
the agent a chance to explicitly specify more general
preference rules to handle any possible conflict that he
may foresee. More precisely, we have the following
definition:
Definition 5.1 (Agent’s preferences given opinion).
Given any two consequences x
i
and x
j
and opinion B
i
of agent i, we define x
i
≻
B
i
x
j
, iff ∃D ⊆ B
i
such that
D ⇒ x
i
≻
i
x
j
and that ∄D
′
⊇ D and D
′
⊆ B
i
such that
D
′
⇒ x
j
≻
i
x
i
Again, it should be noted that it is possible to have
both x
i
≻
B
i
x
j
and x
j
≻
B
i
x
i
. In such cases, the agent’s
preferences are in conflict, and one uncertainty in de-
termining the stability of a coalition is how such con-
flicts are resolved by the agents.
RULE BASED STABILITY CRITERIA FOR COALITION FORMATION UNDER UNCERTAINTY
175

6 CU-CORE
We can now define the coalition stability criteria. The
result is denoted by a new concepts, namely the CU-
core. The CU-core of a coalition is defined by two
sets, namely the set of conditionally stable solutions
(c-core) and the set of unconditionally stable solutions
(u-core). The main idea is as follows: we say a con-
sequence x is definitely objected by a sub-coalition if
there is another consequence y such that every mem-
ber in the sub-coalition would certainly prefer x over
y. We say a consequence x is potentially objected by
a sub-coalition if there is an alternate consequence y
such that every member in the sub-coalition may pre-
fer x over y, as suggested by their preference rules and
opinions. We say a consequence is in the u-core if it
has no definite or potential objection, and we say a
consequence is in the c-core if it has no definite ob-
jection.
Definition 6.1.1 (Conditionally Stable Solutions).
The c-core of a coalition is the set of feasible con-
sequence X
ccore
, such that for each x ∈ X
ccore
, there
does not exist another feasible consequence x
′
∈ X
and a sub-coalition C
′
⊆ N, such that we have x
′
≻
B
i
x
holds but not x ≻
B
i
x
′
for each member i ∈ C
′
.
Definition 6.1.2 (Unconditionally Stable Solutions).
The u-core of a coalition is the set of feasible con-
sequence X
ucore
, such that for each x ∈ X
ucore
, there
does not exist another feasible consequence x
′
∈ X
and a sub-coalition C
′
⊆ N, such that we have x
′
≻
B
i
x
for each member i ∈ C
′
.
In Example 1, for the n
1
= {A
1
, A
2
} coali-
tion, the consequence x
1
= (
movie, movie
) is
in both u-core and c-core, whereas the x
2
=
(
tennis, tennis
) consequence is in neither core.
For the n
2
= {A1, A2, A3, A4} coalition, the con-
sequence x
3
= (
movie, movie, movie, movie
)
consequence is in c-core only, whereas x
4
=
(
tennis, tennis, tennis, tennis
) is in neither
core. Thus we see that the (n
1
, x
1
) solution is the most
stable among the four, and is therefore a good candi-
date solution that should be considered by coalition
formation mechanisms, while (n
1
, x
2
) and (n
2
, x
3
) are
the least stable and should be rejected.
In general, we have the follow result:
Theorem 1. For a given coalition, any consequence
that is in the u-core is also in the c-core.
Proof. This follows directly from the definitions 6.1.1
and 6.1.2
7 APPLICATION AREAS
In this section, we summarize several application
areas where we believe the proposed CU-core can
provide a useful solution concept.
Applications in non-transferable utility game
While the existing probabilistic approaches define
stability concepts on an important class of uncertain
coalition game with transferable utility, there are
many applications where it is more natural to describe
the game in terms of agents’ preference instead of
transferable utilities. For example, in Example 1,
it would be sufficient for an agent to simply state
“I prefer movie over tennis if the movie is good.”
instead of stating “My utility for the movie is 0.5,
whereas my utility for tennis is 0.2, given that the
quality is good.” And even if the utilities are stated in
the latter way, they are likely not transferable utilities.
The problem here is, of course, the probabilistic
approaches cannot be easily applied to this more
general class of non-transferable utility games.
Agents with case-based decision model
As mentioned above, not all decision systems
are probabilistic in nature. For instance, case base
reasoning (CBR) is an important decision making
approach in many artificial intelligent systems (Plaza
and Mcginty, 2005). In a typical CBR system, a case
base with known outcome is maintained. To solve
a new problem, the attributes of the new problem
is compared against the known cases in the case
base. A best match is found and the outcome of that
best match is then used as the proposed solution for
the new problem. CBR is typically used where the
problem space is large so that there are not sufficient
samples to provide a reasonable probabilistic model
for the whole problem space, as required by the
probabilistic approaches. The stability concept we
proposed is much more suitable for multi-agent
applications employing such decision models.
8 RELATED WORKS
We discuss some related works in this section. A
Bayesian-core concept is proposed in (Chalkiadakis
and Boutilier, 2004) where the agents are assumed to
belong to various types which are unknown to other
agents. The agents are required to estimate the value
of potential coalitions by maintaining a Bayesian be-
ICEIS 2007 - International Conference on Enterprise Information Systems
176

lief system regarding the possible types of their po-
tential partners and update their beliefs in a reinforce-
ment learning based approach in repeated games sce-
nario. As mentioned above, our work differs from
theirs in that we do not pre-assume any probabilis-
tic models in particular, and that our model assumes
the more general problem of non-transferable utilities
games, instead of transferable one.
A solution concept for coalition game with
stochastic payoff is presented in (Suijs et al., 1999). In
this approach, the payoffs (i.e., the consequences) are
assumed to be stochastic variables, and agents pref-
erences over those stochastic variables are used to de-
termine the stability of a coalition. Thus, their work is
on stochastic games, whereas our focus is on a more
general class of non-transferable utility game that are
not necessarily probabilistic in nature.
A mechanism for forming coalition under uncer-
tainty is proposed in (Kraus et al., 2003; Kraus et al.,
2004). In these two works, a multi-rounds mecha-
nism is proposed where, in each round, the agents are
arranged in a certain order and they make coalition
formation proposals or accept proposals in that order.
The mechanism repeats until each agent belongs to a
coalition. Again, the difference is that their approach
is based on the assumption of transferable utility and
the kernel is used as the stability concept, which is not
our assumption.
9 CONCLUSION
Classical coalition formation concepts in game the-
ory are deterministic in nature. That is, they as-
sume the value of each coalition to be publicly known
for certain. However this assumption is not practi-
cal in many software agent applications where intel-
ligent agents have to rely on whatever evidences they
can perceive or their past experience to estimate such
coalition values. The probabilistic approaches pro-
vide a good alternative in many cases, but are not suit-
able in some multi-agent applications where the sam-
ples are sparse and where the agents utility are non-
transferable. In this paper, we propose a new type of
game which we label non-transferable utility games
with uncertainty, and provide a new concept for de-
scribing the stability of coalitions under uncertainties,
namely, the CU-core. By doing so, we are able to
provide useful stability concepts for this new type of
game which otherwise cannot be handled using the
classic deterministic approaches or the probabilistic
approaches. We believe our model provide a useful
tool in evaluating coalition formation algorithms for
cooperative games under uncertainty.
REFERENCES
Blankenburg, B. and Klusch, M. (2004). Pon safe ker-
nel stable coalition forming among agents. In Pro-
ceedings of the Third International Joint Conference
on Autonomous Agents and Multiagent Systems, vol-
ume 2, pages 580–587.
Chalkiadakis, G. and Boutilier, C. (2004). Bayesian rein-
forcement learning for coalition formation under un-
certainty. In Proceedings of the Third International
Joint Conference on Autonomous Agents and Multia-
gent Systems, pages 1090–1097.
Gillies, D. B. (1959). Solutions to general non-zero-sum
games. InTucker, A. W. and Luce, R. D., editors, Con-
tributions to the Theory of Games Volume IV. Prince-
ton University Press.
He, L. and Ioerger, T. (2004). Combining bundle search
with buyer coalition formation in electronic markets:
A distributed approach through negotiation. In Pro-
ceedings of the Third International Joint Conference
on Autonomous Agents and Multiagent Systems, pages
1440–1441.
Ketchpel, S. (1994). Forming coalitions in the face of uncer-
tain rewards. In Proceedings of National Conference
on Artificial Intelligence (AAAI-94), pages 414–419.
Kraus, S., Shehory, O., and Taase, G. (2003). Coalition for-
mation with uncertain heterogeneous information. In
Proceedings of the Third International Joint Confer-
ence on Autonomous Agents and Multiagent Systems,
pages 1–8.
Kraus, S., Shehory, O., and Taase, G. (2004). The advan-
tages of compromising in coalition formation with in-
complete information. In Proceedings of the Third In-
ternational Joint Conference on Autonomous Agents
and Multiagent Systems, pages 588–595.
Osborne, M. J. and Rubinstein, A. (1994). A Course in
Game Theory. The MIT Press.
Plaza, E. and Mcginty, L. (2005). Distributed case-
based reasoning. The knowledge Engineering Review,
00:01-4.
Sandholm, T. (1999). Distributed rational decision making.
In Weiss, G., editor, Multiagent Systems A Modern
Approach to Distributed Artificial Intelligence. The
MIT Press.
Scarf, H. (1967). The core of n person game. Econometrica,
35(1):50–59.
Suijs, J., Borm, P., Waegenaere, A. D., and Tijs, S. (1999).
Cooperative games with stochastic payoffs. European
Journal of Operational Reseach, 133.
Yamamoto, J. and Sycara, K. (2001). A stable and efficient
buyer coalition formation scheme for e-marketplaces.
In Proceedings of the Fifth International Conference
on Autonomous Agents, pages 576–583.
RULE BASED STABILITY CRITERIA FOR COALITION FORMATION UNDER UNCERTAINTY
177
