REACTIVE COMMONSENSE REASONING

Towards Semantic Coordination with High-level Speciﬁcations

Michael Cebulla

Institut f

ur Softwaretechnik und Theoretische Informatik, Technische Universit

at Berlin

Franklinstraße 28/29, 10587 Berlin, Germany

Keywords:

Context-Awareness, Commonsense Reasoning, Semantic Coordination.

Abstract:

In contemporary distributed applications questions concerning coordination have become increasingly urgent.

There is a trade-off however to be made between the need for a highly reactive behavior and the need for

semantically rich high level abstractions. Especially w.r.t. context-aware applications where various systems

have to act together and come to coordinated conclusions the need for powerful semantic abstractions is

evident. In our argument we start with a calculus for highly reactive behavior. Then we introduce stepwise

two extensions w.r.t. the representation of semantic relationships. The ﬁrst extension concerns the integration

of description logics in order to represent statements about the current situation. The main extension however

concerns the integration of classiﬁcations (also known as formal contexts). By integrating these highly abstract

notions into our membrane-based calculus we make a proposal for the support of common sense reasoning

during runtime. The main purpose of the resulting framework is to provide a generic notion of context which is

accessible for a rigorous computational treatment during runtime. We claim that this proposal is a contribution

to the robustness of systems behavior and context-awareness.

1 INTRODUCTION

In this paper we make an attempt to bridge the gap

between highly reactive behavior during runtime and

the need for highly abstract and meaningful concepts

for context-awareness. Especially we propose to inte-

grate highly abstract forms of commonsense reason-

ing (Barwise and Seligman, 1997; Ganter and Wille,

1997) with membrane computing (P

aun, 2000) in or-

der to support a way of runtime reasoning whose

robustness is comparable to human reasoning. By

this proposal we extend previous suggestions con-

cerning concepts for high-level and intuitive speciﬁ-

cations (Pepper et al., 2002). Our general intent is

directed towards a generic treatment of contextual in-

ﬂuences during runtime.

While classiﬁcations and formal contexts heav-

ily rely on universal algebra and category the-

ory (Goguen, 2005) we propose an operational foun-

dation using membrane computing. In this paper we

focus on the treatment of quotients of classiﬁcations

w.r.t. speciﬁc invariants. Quotients are formal con-

structs which provide powerful support for common

sense reasoning. Using these mechanisms systems

can make inferences about the current situation dur-

ing runtime. In order to ﬁnd out whether an invariant

holds in the current situation the system has to derive

the quotient of the classiﬁcation describing the cur-

rent situation and a speciﬁc invariant. This invariant

then can be considered as a request. If the quotient is

not empty the invariant holds.

Related Work. Important and inﬂuential treatments

of the notion of context are (McCarthy, 1997; Sowa,

2000). Even more rigorous treatments can be found

in (Barwise and Seligman, 1997; Ganter and Wille,

1997; Goguen, 2005). Our discussion is basically in-

spired by (Barwise and Seligman, 1997) shifting the

focus to an operational treatment of runtime infer-

ences.

In the following we brieﬂy describe the formal

foundations of our approach in Sections 2- 4. Then

we describe the notions of invariants and quotients

and discuss their algorithmic treatment in our frame-

113

Cebulla M. (2007).

REACTIVE COMMONSENSE REASONING - Towards Semantic Coordination with High-level Speciﬁcations.

In Proceedings of the Ninth International Conference on Enterprise Information Systems - AIDSS, pages 113-118

DOI: 10.5220/0002408201130118

 SciTePress

Figure 1: Intuition: Membrane System (Bernardini, 2005).

work. We claim that this approach is quite powerful

since it supports the reasoning about different types

of relations in different types of logics. Examples are

various types of modal and behavioral logics. In or-

der to give an impression of the power of the approach

we take an example from the literature which is quite

relevant for questions concerning coordination in dis-

tributed systems.

2 MEMBRANE COMPUTING

In this Section we describe membrane-based P-

systems (P

aun, 2000) as building blocks for the de-

scription of complex systems. Thus a transition P-

system is basically deﬁned as a constraint store whose

behavior is described by CHAM-like transition rules

for multiset rewriting (Ban

atre and Metayer, 1993).

P-Systems are deﬁned on membrane structures as fol-

lows (slightly adapted from (P

aun, 2000; Bernardini,

2005)):

Deﬁnition 1 (P-System) A P-system of degree m is

deﬁned as a tuple

Π = hV,C, µ,w

,... ,w

,(R

,ρ

),. .. ,(R

,ρ

),i

where V is an alphabet of symbols (called objects),

C ⊆ V is a subset called catalysts, µ is a membrane

structure, w

,.. .,w

are fuzzy multisets of objects

from V, R

,.. .,R

are sets of transformation rules as-

sociated with the regions, ρ

are the priority relations

between these rules and i

is the output membrane. 2

The symbols ofV are treated as molecules ﬂoating

in a speciﬁc solution. These (sub-)solutions are also

referred to as regions (cf. Figure 1). Regions are asso-

ciated with a membrane which contains them. Addi-

tionally transformation rules are associated to regions

which deﬁne local behavior.

Adaptivity, Self-Optimization. We chose this

highly reactive semantic model as the basis of our

process description because we feel that it is appro-

priate for the description of unexpected behavior. Es-

pecially, environmental changes or unexpected con-

textual inﬂuences can be modeled by introducing new

molecules into the solution. Thus, the actual state of

a P-system is described by the states of its regions.

The terms in these regions can be processed using the

transition rules or can be propagated to other regions

by diffusion through porous membranes.

Rules. Rules in P-systems are of the following form

aun, 2000):

Deﬁnition 2 (Rules) Rules in P-systems are of the

form u → v with u ∈ V

and v ∈ (V × Tar)

∗

, where

Tar = {here,in,out}. 2

While u in this kind of rules is a multiset overC, v

is a pair whose ﬁrst element is an element of C while

the second element is taken from {here,in,out}. The

latter keywords (also called target commands) specify

the direction into which v has to be moved. Rules are

associated with regions. In each step of the behavior

of a P-system a transition takes place which consists

of the application of all applicable rules in all regions.

The rules are applied in a non-deterministic and max-

imal parallel manner.

Remark. In our discussion we silenlty introduce a

fuzzy version of P-systems.

3 FUZZY DESCRIPTION LOGICS

For the fuzziﬁcation of description logics fuzzy sets

(Zadeh, 1965) are introduced into the semantics in-

stead of the crisp sets used in the traditional seman-

tics cf. (Baader and Nutt, 2003). For more detailed

discussion of these issues cf. e.g. (Straccia, 2001;

odobler et al., 2003).

Deﬁnition 3 (Fuzzy Interpretation) A fuzzy inter-

pretation is a pair

I = (∆

,·

), where ∆

is, as for the

crisp case, the domain whereas ·

is an interpretation

function mapping

1. individuals as for the crisp case, i.e. a

6= b

, if

a 6= b;

2. a conceptC into a membership functionC

: ∆

→

[0,1];

3. a role R into a membership function R

: ∆

∆

→ [0,1].

ICEIS 2007 - International Conference on Enterprise Information Systems

114

If C is a concept then C

will be interpreted as the

membership degree function of the fuzzy concept C

w.r.t.

I . Thus if d ∈ ∆

is an object of the domain ∆

then C

(d) gives us the degree of being the object d

an element of the fuzzy concept C under the interpre-

tation

I (Straccia, 2001). For some selected construc-

tors which were considered for description logics the

interpretation function ·

has to satisfy the following

equations:

⊤

(d) = 1

⊥

(d) = 0

(C⊓ D)

(d) = min(C

(d),D

(d))

(C⊔ D)

(d) = max(C

(d),D

(d))

(¬C)

(d) = 1−C

(d)

(∀R.C)

(d) = inf

′

∈∆

{max(1− R

(d,d

′

),C

′

)}

(∃R.C)

(d) = sup

′

∈∆

{min(R

(d,d

′

),C

′

)}

(∀T.C)

(d) = inf

′

∈∆

{max(1− T

(d,o),C

(o)}

(∃T.C)

(d) = sup

′

∈∆

{min(T

(d,o),C

(o)}

(qR.C)

(d) = {d|d ∈ ∆

,|{d

′

|R(d,d

′

) > 0}| ≥ q}

(mod

R.C)

(d) = {d|d ∈ ∆

,mod(|{d

′

|R(d,d

′

) > 0}|) ≥ q}

Quotient-based Reasoning. Deviating from com-

mon approaches based on description logics we do

not focus on model-based reasoning about satisﬁa-

bility or subsumption. This is the reason why we

do not rely on tableaux-based reasoning and thus do

not have to face the resulting computational complex-

ity (Baader and Nutt, 2003). In contrast we pro-

pose an automata-based approach for reasoning about

the conformance of systems w.r.t. certain invariants.

Speciﬁcations are considered invariants for which the

quotients are computed by tuple automata. Note that

we have our restrict our attention to the treatment of

crisp invariants in this paper due to space limitations.

It is well-known that this type of invariant can be con-

sidered as a special case of fuzziness.

4 CLASSIFICATIONS: FORMAL

CONTEXTS

In this Section we brieﬂy describe the integration of

high-level modeling into the reactive calculus.

4.1 Information Systems

The abstract notion of information systems has been

introduced by (Barwise and Seligman, 1997) as ab-

stract description of components in distributed sys-

tems.

Information Systems. Information systems are de-

ﬁned by classiﬁcations.

Deﬁnition 4 (Classiﬁcation) A classiﬁcation A =

htok(A),typ(A),|=

i is a triple where tok(A) is a set

of tokens (object), type(A) is a set of types classifying

tokens, and |=

is a binary relation between tok(A)

and typ(A). 2

The notion of classiﬁcation can be represented

by P-systems. We establish this connection in order

to provide an operational semantics for knowledge-

based reasoning. We exploit in this representation the

similarities between classiﬁcations, knowledge bases

(e.g. for description logics) and formal contexts. Gen-

erally the following components are used (we ignore

the terminological differences between the notions

from different approaches):

Types. The sets of concepts and of roles constitute

the vocabulary of the type language. The alphabet

V from the deﬁnition of P-systems consists from

the set C of concepts and the set R of roles. Intu-

itively these sets contain the vocabulary (i.e. the

signature) which can be used in the current con-

text.

Individuals. Names for individuals which are also

part of the TBox in case of knowledge bases are

treated as tokens in classiﬁcations. In our ap-

proach based on P-systems a set of individual

names is part of the type language.

Classiﬁcation Relation. In the case of knowledge

bases this relation is described by the expressions

in the ABox. Basically it deﬁnes which types are

applicable to which individuals.

Simulation. Under operational criteria we represent

classiﬁcations as P-systems P

. Basically a classi-

ﬁcation is enclosed by a membrane. On the back-

ground of our discussion we distinguish three subsys-

tems in P

: a signature, a set of axioms, and a set of

sentences. These entities are mapped to components

from P-systems.

Deﬁnition 5 (Classiﬁcation P-System P

) The P-

System for the representation of classiﬁcations P

deﬁned by the tuple hV,L, µ,w

,Ri whereV = C∪R∪I

is the terminology of the classiﬁcation (i.e. the sig-

nature or the type set or the TBox), the label set

L = C∪R. The initial membrane structure µ = [

[

]

contains an empty membrane representing an ABox.

Example 1 (Simple Classiﬁcation.) We use a table

for the classiﬁcation of patients according to gender

resulting in the DL-expressions in the bottom part of

Figure 2. ♦

REACTIVE COMMONSENSE REASONING - Towards Semantic Coordination with High-Level Specifications

115

msc x x x

fem x x

msc(p

)msc(p

)fem(p

)

fem(p

)msc(p

)

Figure 2: Classiﬁcation of Patients w.r.t. Gender.

The same situation is represented by the following

P-system:

Deﬁnition 6 (P-system P

) The P-System P

is de-

ﬁned by the tuple hV,L,µ,w

,Ri where

V = {msc, fem}∪ {p

, p

}

is the terminology of the classiﬁcation (i.e. the signa-

ture or the type set or the TBox), the label set L =

C ∪ R. The initial membrane structure µ = [

[

]

contains the multiset

v = [msc(p

),msc(p

), fem(p

),msc(p

)].

4.2 Derivation, Closure

As is well known from the literature classiﬁcations

and formal contexts are essentially the same. The

concepts (in DL-terminology) which are contained in

the type language can be treated as the attributes of

formal contexts while individuals take the role of to-

kens. In FCA-terminology the notions of formal con-

cepts is related to closed theories (Goguen, 2005). In

this Subsection a computational approach to some ba-

sic inference mechanisms is discussed which is used

a a foundation of the quotient-based mechanisms in

Subsection 4.3.

Derivation. As a ﬁrst step we have to describe the

computation of the derivation operator (Ganter and

Wille, 1997). This operator describes the relation be-

tween signatures and models and induces a Galois

connection (Goguen, 2005).

Deﬁnition 7 (Derivation) For a set A⊆ G of individ-

uals the derivation is deﬁned by:

′

:= {m ∈ M|gIm for all g ∈ A}.

for the set of B ⊆ M of attributes:

′

:= {g ∈ G|gIm for all g ∈ A}

where I is the classiﬁcation relation. 2

Again we deﬁne this operator by membrane ma-

nipulations.

Figure 3: Derivation.

Simulation. Thus for a set of attribute names B all

instances have to be collected which satisfy these at-

tribute names in a membrane which is labeled with

′

. The resulting membrane is the intersection of all

membranes which represent concepts contained in B.

[

′

]

′

[

→ [

′

[

,C ∈ B

[

′

[

→ [

′

a∩ b]

′

[

,C ∈ B

An exemplary computation is shown in Figure 3.

The complementary deﬁnition for the derivation op-

erator on sets of instances we use a similar procedure

which operates on the ﬂipped classiﬁcation, cf. (Bar-

wise and Seligman, 1997).

4.3 Quotients of Classiﬁcations

In this Section we describe the computation of quo-

tients which is very important and opens many possi-

bilities of application. As a running example we de-

scribe the reasoning about modalities which can be

mapped to the computation of quotients for classiﬁ-

cations and invariants. The relation of the invariant

then represents the accessibility relation of the Kripke

semantics (Hughes and Cresswell, 1996).

Deﬁnition 8 (Invariant) An invariant I = hΣ,Ri is a

pair of a set of types Σ and a relation R between a set

of tokens from the classiﬁcation. 2

Intuitively we claim that the accessibility relation

of a modal logics is represented by R while the tokens

may be considered as possible worlds. The knowl-

edge which is contained in a classiﬁcation is then ex-

pressed by the set of types Σ which holds in every

possible world. More formally the knowledge which

is contained in a classiﬁcation is represented by the

quotient of the classiﬁcation.

Deﬁnition 9 (Quotient of a Classiﬁcation) Let I =

hΣ,Ri be an invariant on the classiﬁcation A. The

quotient of A by I, written A/I, is the classiﬁcation

with types Σ, whose tokens are the R-equivalence

classes of tokens in A, and with [a]

A/I

α(α ∈ Σ)

iff a |=

α. 2

ICEIS 2007 - International Conference on Enterprise Information Systems

116

There is a close correspondence between the no-

tion of quotient in (Barwise and Seligman, 1997) and

the notion of derivation (of intents) in (Ganter and

Wille, 1997). We thus see an intent as a special case

of invariant (Barwise and Seligman, 1997). One way

to state this correspondence is to claim that an intent

is an invariant (with an unspeciﬁed relation).

Remark. It is possible to model different kinds of

knowledge deﬁning different properties of the rela-

tion R (e.g. reﬂexivity, symmetry and transitivity).

As is well known each of these different types of rela-

tions induce different types of modal logics (Hughes

and Cresswell, 1996). Although the original deﬁni-

tion of invariants assumes equivalence relations we

decided to admit also other types of relations. In these

cases the quotients cannot be considered as equiva-

lence classes anymore.

Example 2 (Quotients of Modalities.) Again we

rely on tables in order to specify situations. We

use a table for the description of classiﬁcation and

another table in order to describe relations (cf. Fig-

ure 4). Again these tables can be easily translated

into expressions from description logics. Note that

we give only one half of the speciﬁcation for the

relations since we assume that they are symmetric.

The situation described in the tables corresponds

to the muddy children puzzle as treated by (Fagin

et al., 1996). A tabular notation is provided for the

easy description of such a situation. The ﬁrst table

describes the set of possible worlds s

which are

characterized by expressions built from the attributes

, where m

denotes the fact that child i has a muddy

forehead. The relations r

described by table 2 on the

other hand describes which world is accessible for

agent i in a given world.

Invariants. We are able to specify invariants hΣ,Ri

on this structure where Σ ⊆ {m1,m2,m3} and R ⊆

{r1, r2,r3}. Using the syntax of description logics

(and exploiting semantic correspondences to the logic

we can express some interesting properties as in-

variants .

∃r1.m1 ⇔ m1 is possible for A

∀r1.m1 ⇔ m1 is necessary for A

By using expressive description logics we are able

to describe more complex modal properties.

∃(r1∪ r2).m1 ⇔ m1 is possible for A

and A

∀(r1∪ r2).m1 ⇔ m1 is distributed knowledge.

∀(r1◦ r2).m1 ⇔ A

knows that A

knows m1

♦

m1 m2 m3

s2 x

s3 x

s4 x x

s5 x

s6 x x

s7 x x

s8 x x x

s1 s2 s3 s4 s5 s6 s7 s8

s2 r3

s3 r2

s4 r2 r3

s5 r1

s6 r1 r3

s7 r1 r2

s8 r1 r2 r3

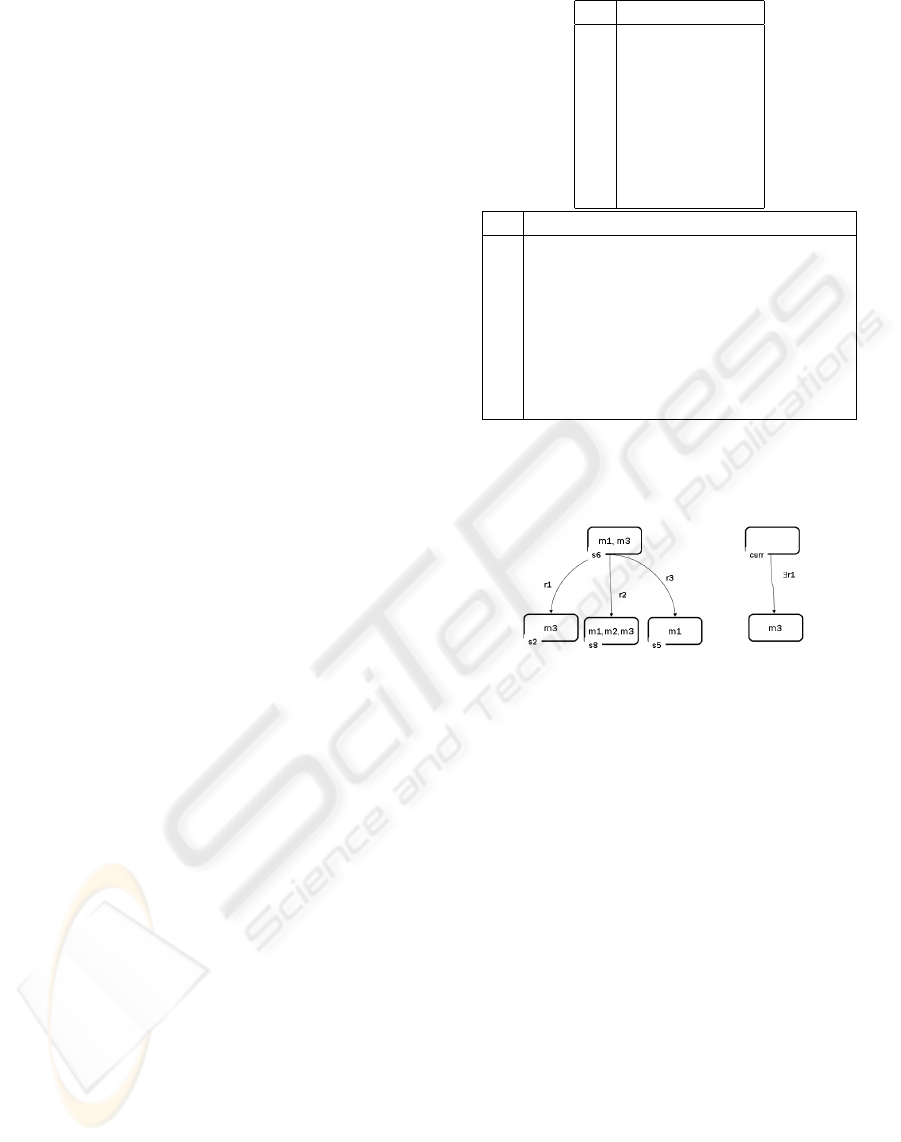
Figure 4: Three Modalities.

Figure 5: Membrane representation of Kripke structures.

Discussion. By the integration of these three meth-

ods in our framework we get an ensemble of intu-

itive speciﬁcation methods which are domain-speciﬁc

and easy to use. Especially for the usage of

domain-experts we propose the usage of tables (as is

widespread in FCA and IFF-theory).

Simulation. In order to treat relations of invariants

in our framework we transform the corresponding ex-

pressions into a membrane-based representation. For

this sake we consider Kripke structures as ﬂipped

classiﬁcations (Barwise and Seligman, 1997). These

are characterized by the fact that the membranes are

labeled by the names of the tokens (i.e. the possible

worlds) while the type names are ﬂoating in the so-

lution. Intuitively each membrane contains the types

which are satisﬁed in the world whose name is used a

label for the membrane. Relations between the worlds

are represented by membrane channels between the

membranes.

For the algorithmic treatment we extensively use

REACTIVE COMMONSENSE REASONING - Towards Semantic Coordination with High-Level Specifications

117

the fact that we can consider speciﬁcations (classiﬁca-

tions as well as invariants) as tree-like term structures.

For example both the systems speciﬁcation as well

as the viewpoint speciﬁcations can be represented in

such a way (cf. Figure 5). Thus the quotient can be

computed by a simple tuple tree automaton which can

be deﬁned using rules of P-systems. For the sake of

brevity we have to skip the details of the algorithmic

treatment.

5 CONCLUSION

Our research is directed towards an integration of

highly reactive behavior on one hand and the support

of common sense reasoning which relies on power-

ful semantic abstractions on the other hand. In this

paper we proposed an approach which contains no-

tions from information ﬂow, formal concept analysis,

description logics and membrane computing in order

to attain this goal. In this paper the speciﬁc contri-

bution is represented by the introduction of classiﬁ-

cations, invariants and quotients into the calculus of

membrane computing. This can be considered as a

foundation for the integration of more complex ab-

stractions.

REFERENCES

Baader, F. and Nutt, W. (2003). Basic description logics.

In Baader, F., Calvanese, D., McGuinness, D., Nardi,

D., and Patel-Schneider, P., editors, The Description

Logic Handbook. Cambridge University Press, Cam-

bridge, U.K.

Ban

atre, J. and Metayer, D. L. (1993). Programming by

multiset transformation. Communications of the ACM,

36:98–111.

Barwise, J. and Seligman, J. (1997). Information Flow: the

logic of distributed Systems. Cambridge Univ. Press.

Bernardini, F. (2005). Membrane Systems for Molecular

Computing and Biological Modelling. PhD thesis,

University of Shefﬁeld.

Fagin, R., Halpern, J. Y., Moses, Y., and Vardi, M. Y.

(1996). Reasoning about Knowledge. The MIT Press,

Cambridge, Mass.

Ganter, B. and Wille, R. (1997). Formal Concept Analysis.

Mathematical Foundations. Springer: Berlin, Heidel-

berg.

Goguen, J. (2005). Information integration in institutions.

In Memorial Volume for Jon Barwise. Indiana Univer-

sity Press, Indiana.

odobler, S., St

orr, H.-P., and Khang, T. D. (2003). The

fuzzy description logic alc

with hedge algebras as

concept modiﬁers. International Journal of Advanced

Computational Intelligence and Intelligent Informat-

ics, 7(3):294–305.

Hughes, G. and Cresswell, M. (1996). A New Introduction

to Modal Logic. Routledge.

McCarthy, J. (1997). Formalizing context (expanded notes).

In Aliseda, A., van Glabbeek, R., and Westerstahl, D.,

editors, Computing Natural Language. Stanford Uni-

versity.

aun, G. (2000). Introduction to membrane computing.

Journal of Computer and System Science, 61(1):108–

143.

Pepper, P., Cebulla, M., Didrich, K., and Grieskamp, W.

(2002). From program languages to software lan-

guages. The Journal of Systems and Software, 60.

Sowa, J. F. (2000). Knowledge Representation. Logi-

cal, Philosophical, and Computational Foudnations.

Brooks/Cole, Paciﬁc Grove.

Straccia, U. (2001). Reasoning with fuzzy description logic.

Journal of Artiﬁcial Intelligence Research, 14:137–

166.

Zadeh, L. A. (1965). Fuzzy sets. Information and Control,

8(3):338–353.

ICEIS 2007 - International Conference on Enterprise Information Systems

118