
Consistency of Loosely Coupled Inter-organizational
Workflows with Multilevel Security Features
Nirmal Gamia and Boleslaw Mikolajczak
Computer and Information Science Department, University of Massachusetts
285 Old Westport Road,MA 02747, USA
Abstract. The paper presents an algorithm to verify consistency of Inter-
Organizational Workflows (IOWF) with Multi-level Security (MLS) features.
The algorithm verifies whether the implementation of Inter-Organizational
Workflow with Multi-level Security features meets the specification. The
algorithm reduces the workflows of participating organizations using the
reduction rules while preserving the communication patterns between
organizations. The paper presents an algorithm to identify redundant implicit
places in the IOWF with MLS features. We conclude that IOWF with MLS
features is k-consistent with Message Sequence Chart (MSC) if the number and
order of messages passed between organizations in reduced IOWF with MLS
features is same as that in original MSC.
1 Introduction
The motivation for this paper stems from the need of companies involved in e-
commerce to have secure and correct inter-organizational workflows. The Internet,
which is the primary medium for conducting e-commerce, is by design an open non-
secure medium. Inter-Organizational Workflows allow data sharing and work
coordination at the global level as the globalisation of business becomes a common
practice. However, the prolific use of inter-organizational workflows for critical and
strategic applications makes security an essential and integral part. Another major
problem with inter-organizational workflow is that they often use heterogeneous and
distributed hardware and software systems to execute a given workflow. This gives
rise to decentralized security policies and mechanisms that need to be managed.
Inter-organizational workflows merged with multilevel security features provide
the necessary security. However sophisticated techniques are required to review,
analyse, and test this approach for correct behavior because presence of errors can
result in serious consequences [5].
Inter-Organizational Workflow (IOWF) becomes important as it provides solution
for data sharing, heterogeneity in resources and work coordination at global level.
However, a secured computing infrastructure like Multilevel Security (MLS) is
needed to support today’s vast businesses. In this paper Message Sequence Charts
(MSC) are used to specify the positive and negative interactions between
organizations. Petri nets are used to model workflows in each organization. IOWF is
obtained by using message sequence charts and workflows of each organization.
Gamia N. and Mikolajczak B. (2007).
Consistency of Loosely Coupled Inter-organizational Workflows with Multilevel Security Features.
In Proceedings of the 5th International Workshop on Modelling, Simulation, Verification and Validation of Enterprise Information Systems, pages 53-62
DOI: 10.5220/0002413300530062
Copyright
c
SciTePress

2 Inter-organizational Workflows
E-commerce is the process of managing online financial transactions by individuals
and companies. This includes consumer and business-to-business transactions. The
focus of e-commerce is on the systems and procedures whereby financial documents
and information of all types is exchanged.
2.1 IOWF Architectures
This section presents conceptual architectures for supporting inter-organizational
workflows [10]. Capacity sharing architecture assumes centralized control. Even
though the execution of tasks is distributed over the resources of several business
partners, the routing of workflow is under the control of one workflow manager.
Chained execution architecture involves splitting of the workflow process into a
number of disjoint sub-processes that are executed by different participating business
partners in a sequential order. Subcontracting architecture involves one business
partner, which subcontracts sub-processes to other business partners. For the top-level
business partner the subcontracted sub-processes appear to be atomic. Case transfer
architecture (CTA) comprises of each business partner having a copy of the workflow
process description, i.e., the process specification is replicated. It is assumed that each
of the business partners uses the same process definition. Extended case transfer
architecture (ECTA) allows local variations in process definition, i.e., at a specific
location the process may be extended with additional tasks. It is important that the
extensions allow for the proper transfer of cases. Loosely coupled architecture (LCA)
consists of the process being cut into pieces, which may be active in parallel. Also the
definition of each of the sub-processes is local, i.e. the environment does not know the
process. Only the protocol used to communicate is public for the other business
partners. This allows individual organization, in a distributed system, to change
without affecting or requiring change in any other part of the system.
For IOWF we need an architecture that is decentralized, flexible with respect to
local workflow specification, supports hierarchical and non-hierarchical control
distribution, allows parallel execution of workflow and supports distributed
collaboration. Loosely coupled architecture supports all this requirements.
2.2 Multilevel Security
It is a concept involving mandatory access control (MAC), i.e. the system enforces
security policy regardless of the actions of system users or administrators. Multi-level
Security (MLS) systems [7] strive to enforce the security restrictions with incredibly
high reliability so as to not leak any data at all. Any two-security levels can be
compared based upon their clearance levels and classification levels. Given two
security levels, first their clearance levels are compared. If the clearance levels are
different then hierarchical ordering of clearance levels is used to determine which
security level has higher precedence over the other. This is followed by comparison of
their classification levels to determine the reading and writing rights. For example in
54

Figure 1, if we have to compare two security labels T{A, B} and S{A} then we first
conclude that T{A,B} has higher precedence than S{A} based on hierarchical
ordering of classification levels. Then we compare classification levels of two given
security labels. We conclude that T{A,B} can read data labeled S{A} since it contains
the A compartment. If we have to compare security labels T{} and S{A} then we first
conclude that T{} has higher precedence than S{A} based on hierarchical ordering of
classification levels. Then we compare classification levels of two given security
labels. We conclude that T{} cannot read data labeled S{A} since it does not contain
the A compartment.
If clearance levels are same then the classification levels determine the higher
precedence as well as the reading and writing rights. For example in Figure 1, if we
have to compare two security labels T{A,B} and T{A} then based upon classification
levels we conclude that T{A,B} has higher precedence than T{A} and T{A,B} can
read data labeled T{A}.
Algorithm: Merging MLS into IOWF
Input: IOWF
Output: IOWF with MLS features
1. Identify a set of subjects A={A
1
, A
2
,...,A
p
}, where p ≥1 for any of the workflows.
2. Determine a set of hierarchical clearance levels {X
1
, X
2
,...,X
m
} for subjects, where
1 ≤ m ≤ p and X
j
has higher precedence than X
i
for j > i.
3. Identify a set of objects B={B
1
, B
2
, ... ,B
q
} where q ≥ 0 in the same workflow.
4. Determine a set of classification levels {Y
1
, Y
2
,... Y
n
} for objects depending upon
its sensitivity, where 0 ≤ n ≤ q.
5. Combine clearance levels and classification levels to obtain security lattice with
security labels S
k
= X
i
{Y
1
, Y
2
, ... Y
j
} where i ≤ m, j ≤ n, k ≤ m2
n
, as nodes.
6. Assign security labels to subjects and objects taking into account Bell-LaPadula
security model and the working of the participating workflow, to form a security
lattice of applicable security labels. If A is a set of all subjects and S is the set of all
security labels, then there exists a many-to-one onto function f
1
: A → S. If B is a set
of all objects and S is the set of all security labels, then there exists a many-to-one
onto function f
2
: B → S.
7. Repeat steps 1 to 6 for all organizations.
8. Combine security lattices of participating organizations taking into account which
security label can read which other security label, to obtain security lattice for the
whole IOWF. If S
1
and S
2
are two security labels such that S
1
can read S
2
then
introduce an arrow from S
1
to S
2
in the security lattice indicating reading rights.
9. Compare security label of subject with security label of object it is trying to access.
Grant access only if the subject is cleared to access that object, otherwise deny access.
2.3 Bell-LaPadula Security Model
The Bell-LaPadula Model [2], also called the multi-level model, was originally
proposed by in 1970s. It is a formal state transition model of computer security policy
that describes a set of access control rules. In this formal model, the entities in a
computer system are divided into abstract sets of subjects and objects. A "subject" is
somebody (user) who wants access to an "object" (information, data file, system). The
concept of a secure state is defined, and it is proven that each state transition
55

preserves security by moving from secure state to secure state, thereby inductively
proving that the system is secure.
The concept of a secure state is defined by two properties: the simple security (ss)
property and the *-property.
(1) ss-property allows all low-level information to be available at a higher level. It
restricts high-level information to be available at a lower level. A subject is allowed to
read an object only if former security label is identical or higher than latter’s security
label (no read up).
(2) *-property ensures there is no write down. A subject with a higher security
label should not write an object of lower security label. There is a risk of Trojan horse
attack if this is allowed. This security policy prevents the ability of higher security
label subject to put higher security label information to lower security label
information that is equivalent of declassifying information.
Within an organization there are various subjects with hierarchical security levels
ranging from high to low level. Also most organizations have various classification
levels for information, depending upon its sensitivity. Bell-LaPadula security model
requires identification of subjects and objects in the system and assigning security
labels to them. This can be easily done because of the way organizations are
composed. Thus we use Bell-LaPadula model to incorporate multilevel security in
IOWF.
3 Consistency of IOWF with MLS
In IOWFs each business partner has a private workflow process that is connected to
the workflow processes of some of the other partners. It involves communication
between the workflows of all participating organizations. Error in design of IOWF are
thus difficult to detect and can result in some serious consequences. Therefore, there
is need to detect the correctness of the IOWF. There are two concepts to verify the
correctness of IOWF, namely soundness and consistency. A workflow is sound if and
only if, for any case, the process terminates properly, i.e., termination is guaranteed,
there are no dangling tasks and there is no deadlock in the workflow [9]. Consistency
[8] deals with verifying whether the implementation of IOWF meets the specification.
In this paper we address consistency issues of loosely coupled IOWFs.
3.1 Consistency
In order to specify the interaction between the various participating organizations
within an IOWF, Message Sequence Charts (MSCs) are used. MSCs provide partial
order of messages in an IOWF. Therefore IOWF should be designed in such a way
that it should be consistent [8] with the MSC. MSC can be defined as follows [9]:
A message sequence chart is a tuple MSC=(I, M
A
, M
S
, from, to, {
i
≤
}
It∈
)
- I is a finite set of instances (business partners),
- M
A
is a finite set of asynchronous messages,
- M
S
is a finite set of synchronous messages,
56

- M
A
∩ M
S
= Ø and M = M
A
U M
S
is the set of messages,
- to and from are functions from M to I,
- for each i in I: ≤
i
is a partial order on {?m |m in M
A
Λ to(m) = i} U {!m | m in M
A
Λ from(m) = i} U {!?m | m in M
S
Λ i in {to(m), from(m)}}.
Relation between IOWF, MSCs and Local Workflows can be informally expressed
by the following equation
IOWF = MSCs + Local Workflows
According to this equation, if we have local workflows and the specification of
communication patterns between them, we can derive the IOWF. By checking the
consistency of an IOWF we can determine whether the implementation meets the
specification i.e. the MSCs [10].
It is usually difficult to describe all the communication patterns in an IOWF using
MSCs. In most cases only communication patterns are given in terms of limited set of
MSC. In general MSCs and implemented IOWF do deviate from each other. The
participating organizations have to observe these deviations to look whether they are
acceptable or not. Non-acceptable differences can result in modification of IOWF.
As there can be number of admissible patterns, it can be more efficient to specify
negative MSC. Negative MSC corresponds to the communication pattern that should
not occur. In case when negative MSC and MSC coincide then it results in an
inconsistency as there is a pattern that is both acceptable and non acceptable. Such
inconsistency should be removed.
As there can be a number of MSCs describing the behaviour of IOWF verification
of consistency becomes a tough task. This leads to concept of k-consistency where k
is the number of different communicational patterns described by the given MSCs. In
1-consistency it is assumed that all the participating organizations in IOWF adhere to
one predefined communication pattern. Concept of 1-consistency is defined as
follows [10]:
Let IOWF = (PN
1
, PN
2
, ...,PN
n
, P
AC
, AC, T
SC
, SC) be an inter-organizational
workflow and let MSC= (I, M
A
, M
S
, from, to, ,{
i
≤
}
It∈
)) be a message sequence
chart. IOWF is 1-consistent with respect to MSC if and only if
(i) P
AC
= M
A
and T
SC
= M
S
,
(ii) u(IOWF) = (P
U
, T
U
, F
U
) is the unfolding of IOWF with source place denoted as i.
For each t
1
, t
2
in T
U
: if there is a firing sequence starting in state i which fires
transition t
1
before transition t
2
, then
An IOWF is said to be k-consistent with respect to the MSC
(i) If the message names used in positive MSCs are the same as the names of
communication links between the workflows and the order of execution of tasks in
IOWF is the same as that in MSC, and
(ii) It is not be possible to execute any of the scenarios specified in the negative
MSCs.
1-consistency can be verified by generating all possible firing sequences and
checking whether partial order ≤
MSC
is not violated by any of these sequences. Partial
order ≤
MSC
is be defined as follows:
57

Let MSC = (I, M
A
, M
S
, from, to, {
i
≤
}
It∈
) be a message sequence chart such that
≤
inst
= ≤
i
,
≤
oi
= {(!m, ?m) | m in M
A
)},
≤
MSC
= (≤
inst
U ≤
o
)
+
.
≤
MSC
is a transitive closure of partial order between the production and consumption
of asynchronous messages (≤
oi
) and the partial order within the workflow instances
≤
inst
. A MSC is said to be inconsistent if ≤
MSC
does not define a partial order.
3.2 Implicit Places
In order to check the consistency of IOWF, instead of checking all possible firing
sequence the concept of implicit places is used to avoid the problem of state
explosion. A place in a net system is a constraint on the firing of its output transitions.
If the removal of a place does not change the behaviour of the original net system,
that place represents a redundancy [3] in the system and can be removed. A place
whose removal preserves the behaviour of the system is called an implicit place, also
called a redundant place [6]. An implicit or redundant place always contains sufficient
tokens to allow for the firing of transitions connected to it. Behaviour of a net system
implies sequences of fireable transitions and marking of places in the net system. The
behaviour of the net system can be represented by the reachability graph.
Implicit places allow for the efficient verification of consistency. The generalized
concept of implicit place set can be described as follows:
Let (PN, M) be a marked Petri net with PN=(P, T, F) and P
1 ⊆
P. P
1
is an implicit
place set if and only if for every reachable state M’ and any transition t in T: if each
place in (●t\P
I
) contains a token in state M’, then each place in (●t∩P
I
) contains a
token in M’. Place p in P is an implicit place if and only if {p} is an implicit place set.
Implicit place does not influence the behaviour of the workflow. This means that
reachability graphs of workflows with implicit places and without implicit places are
the same. Removal of implicit places is significant especially in larger workflows.
If p is not the only input place of its output transition, then p may be implicit. If a
transition has only one input place then that input place cannot be implicit, because in
order for the transition to fire, the input place must be present and eventually be
marked. In other words, we need to analyse only those input places for which the
connected transitions have more than one input place.
Hence we first need to identify transitions with more than one input place and
form a set T
P
of such transitions. Next we form a set of input places to any transition
in T
P
and denote it as P
P
. Now we are ready to define the concept of implicit place.
Let (PN, M) be a marked Petri net with PN=(P, T, F) with P
P ⊆
P and T
P ⊆
T
such that T
P
is a set of transitions with more the one input place and P
P
is set of places
corresponding to ●T
P
. If there is a path from ●p
i
excluding p
i
to any one of the other
places corresponding to identical rows in Pre [P
P
, T
P
] then p
i
is implicit. Below we
present an algorithm to identify implicit places in a workflow.
58

Algorithm: Identification of Implicit Places
Input: Petri Net representation of a workflow
Output: Petri Net representation of the workflow without implicit places
1. For a given workflow identify a set T
p
={t
1
, t
2
,...,t
n
} where n ≥ 0 of transitions with
more the one input place.
2. Identify a set P
p
={p
1
, p
2
,...,p
m
} where m ≥ n of input places corresponding to
transitions in the above set T
p
.
3. If there is a path from ●p
i
excluding p
i
to any one of the other places
corresponding to identical rows in Pre[P
p
, T
p
] then p
i
is implicit.
4. Repeat steps 1 to 3 for all places corresponding to identical rows in Pre[P
p
, T
p
].
Algorithm: Verification of Consistency of IOWF with MLS Features
Input: Petri Net representation of IOWF with MLS features
Output: Boolean (is k-consistent or not k-consistent)
1. For all transitions having more than one input places not connected to any other
transitions, replace these input places by a single input place.
2. In IOWF with MLS features, apply reduction rules to reduce local workflow
structure without modifying places and transition that correspond to messages
passed between local workflows.
3. Unfold the reduced IOWF obtained after steps 1 and 2.
4. Identify and remove all implicit places.
Fig. 1. Workflow without implicit places.
5. Repeat steps 1 to 4 till it is not possible to reduce the local structure any further.
6. Check to see if name, number and order of messages passed between local
workflows are same as that in the positive MSCs.
7. Check to see if it is not possible to execute any of the negative MSCs.
8. If result of step 6 and step 7 is positive then conclude IOWF is k-consistent with
MSCs else conclude IOWF is not k-consistent with MSCs.
We now compare the workflow in Figure 3 with the MSCs. We need to check if it is
possible to execute all positive scenarios in the above model. We do this by checking
that name, number and order of messages passed between local workflows is same as
that in the positive message sequence charts. At times it is possible to fire two
different transitions. For example, a token is placed in the place ‘Tires order’ when
‘Send tire order’ fires. This enables transitions ‘Timeout’ and ‘Receive tire order’. If
59

transition ‘Timeout’ fires then a token is removed from ‘Tires order’ place and a
token is placed in ‘Tire order ready’ place. This enables transition ‘Send tire order’
again. In this scenario, tire order is sent first, followed by occurrence of a timeout,
which is followed by resending of the tire order. This scenario is depicted in message
sequence chart shown in Figure 2. If ‘Receive tires order’ transition is fired then any
of the remaining three positive scenarios can occur. Three transitions ‘Send
unavailable’, ‘Suggest modification’ and ‘Send tire order acknowledgement’ are
enabled. Depending upon which transition fires, any one of the remaining three
positive scenarios can occur. Lets say, transition ‘Send tire order acknowledgement’
fires then scenario corresponding to message sequence chart shown in Figure 2
occurs.
Fig. 2. MSC with successful ordering.
From Figure 3 we also note that there is no message passing between
organizations that facilitate order cancelling or sending of order updates. Once the
Tire Company receives tires order and begins processing the order, it is not possible
to ship the built tires without sending tire order acknowledgement. This rules out the
scenario with no acknowledgment. Lastly, it is not possible for Tire Company to send
acknowledgement or ship built tires without receiving the tires order. Thus it is
possible to execute all positive scenarios and prevent all negative scenarios from
occurring in the model shown in Figure 3. We can say that IOWF is k-consistent with
the provided message sequence charts.
4 Conclusions
We developed algorithms to verify consistency of IOWF with MLS features
composed of n local workflows. We also have shown that given one or more positive
MSCs that specify the communication between business partners, it is possible to
verify whether the IOWF is k-consistent with the MSCs. For k-consistency the
concept of reduction rules and the algorithm to identify implicit places were used.
Using algorithms presented companies involved in e-commerce can analyse and test
IOWF for correct behaviour. Future work will aim at using Hierarchical and Coloured
Petri nets for representation of even more complex IOWF.
60

References
1. Atluri V. and Huang W.K., “An Authorization Model for Workflows”, Proc. of the Fifth
European Symposium on Research in Computer Security, Rome, Italy, LNCS, No.1146,
Springer-Verlag, pp. 44-64, 1996.
2. Atluri V. and Huang W.K., “An Extended Petri Net Model for Supporting Workflows in a
Multilevel Secure Environment”, Proc. of the IFIP Working Conference on Database
Security, pp. 199–216, 1996.
3. Berthelot G., “Transformations and Decomposition of Nets”, In Advances in Petri Nets
1986 Part I: Petri Nets, central models and their properties, Lecture Notes in Computer
Science, Volume 254, pp. 360–376. Springer-Verlag, Berlin, 1987.
4. Clark D.D. and Wilson D.R., “A Comparison of Commercial and Military Computer
Security Policies”, In Proceedings of IEEE Symposium on security and Privacy, pp. 184-
194, 1987.
5. Gami, N., Mikolajczak, B., “Integration of Multilevel Security Features Into Loosely
Coupled Inter-Organizational Workflows”, Proc. of the Int. Conference on Information
Technology New Generations, ITNG’ 2007, Las Vegas, NV, April 12-15, 2007.
6. Girault, C., Valk R., “Petri Nets for Systems Engineering: a Guide to Modelling,
Verification, and Applications”, Springer, pp. 278-281, 2003.
7. Knorr K., “Multilevel Security and Information Flow in Petri Net Workflows”, Proc. of the
11th Conference on Advanced Information Systems Engineering, Heidelberg, Germany,
2001.
8. Li X., Hu J., Bu L., Zhao J. and Zheng G., “Consistency Checking of Concurrent Models
for Scenario-Based Specifications”, Proc. of 12th International SDL Forum, Grimstad,
Norway, pp. 298-312, 2005.
9. W.M.P. van der Aalst, “Inter-organizational Workflows: An Approach based on Message
Sequence Charts and Petri Nets”, Systems Analysis - Modelling - Simulation, pp. 335-367,
1999.
10. W.M.P. van der Aalst, “Process-oriented architecture for electronic commerce and inter-
organizational workflow”, Information Systems, pp. 639-671, 2000.
61
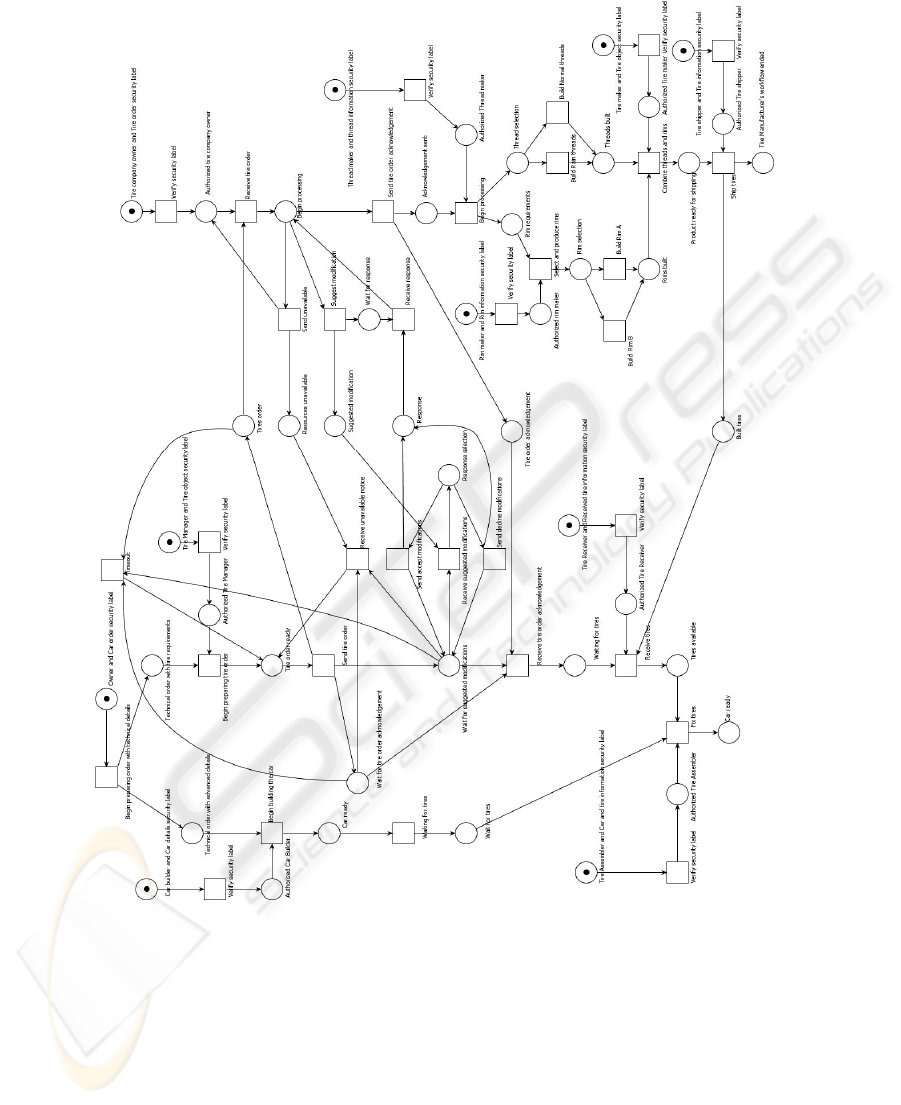
Fig. 3. IOWF with MLS for Car and Tire companies.
62
