
Using Wavelets based Feature Extraction and Relevance
Weighted LDA for Face Recognition
Khalid Chougdali, Mohamed Jedra and Nouredine Zahid
Laboratory of conception and systems, Faculty of Science Agdal
Rabat, Morocco
Abstract. In this work, we propose an efficient face recognition system which
has two steps. Firstly we take 2D wavelet coefficients as a representation of faces
images. Secondly, for recognition module we present a new variant on Linear
Discriminant Analysis (LDA). This algorithm combines the advantages of the re-
cent LDA enhancements namely relevance weighted LDA and QR decomposition
matrix analysis. Experiments on two well known facial databases show the effec-
tiveness of the proposed method. Comparisons with other LDA-based methods
show that our method improves the LDA classification performance.
1 Introduction
Face recognition has become a very active research area in the last decade due to the
interest in video surveillance, access control and security. Although there are many al-
gorithms for face recognition which work well in constrained environments, various
changes in face images present a great challenge, and a face recognition system must
be robust with respect to the much variability of face images such as facial expression,
pose and illumination. To handle with this problem it is important to choose a suit-
able representation of face images. In this paper we propose to use a multilevel two
dimensional (2D) discrete wavelet transform (DWT) [1] to decompose face images and
choose the lowest resolution subband coefficients for robust face representation with re-
gard to lighting changes and ability of extracting important facial features while keeping
computational complexity low. This facial features are taken as entry of an LDA [2] al-
gorithm to find the optimal projection so that the ratio of the traces of the between-class
and the within-class scatter matrices of the projected samples reaches its maximum.
However, a critical issue using LDA, particularly in face recognition area, is the Small
Sample Size (SSS) Problem. To overcome this limitation many LDA-based methods
have been proposed. Among them, the most popular one is to use principal components
analysis (PCA) as a pre-processing step aiming to reduce the dimensionality prior to
performing LDA [3], [4]. Recently, Ye et al [5] have presented the so-called LDA/QR
algorithm as an alternative way to handle the SSS Problem by using QR decomposi-
tion. Moreover, [6] has been shown that the class separability criterion that classical
LDA maximize is not necessarily representative of classification accuracy and the re-
sulting projection will preserve the distances of already well-separated classes while
Chougdali K., Jedra M. and Zahid N. (2007).
Using Wavelets based Feature Extraction and Relevance Weighted LDA for Face Recognition.
In Proceedings of the 7th International Workshop on Pattern Recognition in Information Systems, pages 183-188
DOI: 10.5220/0002413601830188
Copyright
c
SciTePress

causing unnecessarily overlap of neighbouring classes. To solve this problem Loog et
al [6] have proposed an extended criterion by introducing a weighting scheme in the es-
timation of between class scatter matrix. From the similar standpoint [8] have extended
this concept to estimate the within class scatter matrix by introducing the inter-class
relationships as relevance weights. He has presented an LDA enhancements algorithm
namely relevance weighted LDA (RW-LDA) by replacing the unweighted scatter ma-
trices through the weighted scatter matrices in the classical LDA method. Still, this
algorithm cannot directly applied for face recognition because of the singularity of the
weighted within class scatter matrix. In this paper we propose a solution to this problem
by introducing a QR decomposition matrix analysis on RW-LDA and make it applicable
for face recognition. . The rest of the paper is organized as follows: In the next section,
we briefly review related work on some LDA based methods for linear dimension re-
duction. Section 3 introduces the new proposed algorithm. Experiments and discussions
are presented in Section 4. We draw the conclusion in Section 5.
2 Related Works
Firstly some assumptions and definitions will be presented. Given data matrix X ∈
IR
d×n
, classical LDA aims to find a transformation matrix W = [w
1
,...,w
`
] ∈ IR
d×`
,
that maps each column x
i
of X, for 1 ≤i ≤ n, in the d−dimensional space to a vector y
i
in the `−dimensional space as follows:
W : x
i
∈ IR
d
→ y
i
= W
t
x
i
∈ IR
`
(` < d).
Assume that the original data in X is partitioned into c classes. X
i
∈ IR
d×n
i
is the
data matrix containing only the data points from the i
th
class, where n
i
is the size of the
i
th
class and n =
∑
c
i=1
n
i
. An optimal transformation W that preserves the given cluster
structure can be approximated by finding a solution of the following criterion:
J(w) = trace((W
t
S
w
W )
−1
(W
t
S
b
W )). (1)
Where,
S
b
=
c
∑
i=1
p
i
(m
i
−m)(m
i
−m)
t
= H
b
H
t
b
. (2)
S
w
=
c
∑
i=1
p
i
n
i
∑
j=1
(x
i j
−m
i
)(x
i j
−m
i
)
t
= H
w
H
t
w
. (3)
e
i
= (1, . . . , 1) ∈ IR
d×c
, m
i
denotes the mean of class i with prior probability p
i
=
n
i
n
and m is the total mean; x
i j
is the d−dimensional pattern j from class i. The classi-
cal LDA criterion in (1) is not optimal with respect to minimizing the classification
error rate in the lower dimensional space. He tends to overemphasize the classes that
are more separable in the input feature space. As a result, the classification ability will
be impaired. To deal with this problem, Loog et al. [6] have proposed to introduce a
weighting function to the discriminant criterion, where a weighted between-class scat-
ter matrix is defined to replace the conventional between-class scatter matrix. Classes
184

that are closer to each other in the output space, and thus can potentially impair the clas-
sification performance, should be more heavily weighted in the input space. According
to [6], weighted between-class scatter matrix
ˆ
S
b
can be defined as:
ˆ
S
b
=
c−1
∑
i=1
c
∑
j=i+1
w(d
i j
)p
i
p
j
(m
i
−m
j
)(m
i
−m
j
)
t
. (4)
Where p
i
and p
j
are the class priors, d
i j
is the Euclidean distance between the means of
class i and class j. The weighting function w(d
i j
) is generally a monotonically decreas-
ing function defined as in [7]:
w(d
i j
) = d
−2h
i j
with d
i j
=
m
i
−m
j
, h ∈ ℵ. (5)
Recently, [8] has extended the concept of weighting to estimate a within-class scat-
ter matrix. Thus by introducing a so-called relevance weights, a weighted within-class
scatter matrix
ˆ
S
w
is defined to replace a conventional within-class scatter matrix:
ˆ
S
w
=
c−1
∑
i=1
p
i
r
i
n
i
∑
j=1
(x
i j
−m
i
)(x
i j
−m
i
)
t
with r
i
=
∑
j6=i
1
w(d
i j
)
. (6)
Using the weighted scatter matrices
ˆ
S
b
and
ˆ
S
w
the criterion in (1) is weighted and the
resulting algorithm is referred to as relevance weighted LDA (RW-LDA).
3 The Proposed Algorithm
It is easy to verify that when a small sample size problem takes place, such as in the face
recognition area, both S
w
and
ˆ
S
w
are singular and then RW-LDA cannot be used directly.
To overcome this problem, we propose to use QR decomposition matrix analysis [9] as
in LDA/QR but with the modified expressions of H
b
and H
w
defined as follows:
ˆ
H
b
=
α
12
(m
1
−m
2
),...,α
(c−1)c
(m
c−1
−m
c
)
. (7)
ˆ
H
w
= [β
1
(X
1
−m
1
e
1
),...,β
c
(X
c
−m
c
e
c
)]. (8)
So that
ˆ
S
b
=
ˆ
H
b
ˆ
H
t
b
and
ˆ
S
w
=
ˆ
H
w
ˆ
H
t
w
, where α
i j
=
p
p
i
p
j
w(d
i j
) and β
i
=
√
p
i
r
i
. with a
weighting function w(d
i j
) = ((m
i
−m
j
)
t
(m
i
−m
j
))
−h
, h ∈ ℵ.
The steps for the proposed RW-LDA/QR algorithm are presented by the following
pseudo code:
4 Experimental Results
The proposed method is tested by two group experiments corresponding to ORL[10]
and Yale[11] faces databases. The test protocol is the same in the both experiments.
First Group: The ORL face database consists of images from c = 40 different peo-
ple, using 10 images from each person, for a total of 400 images. Firstly we down
185
Input: Data matrix X, h.
Output: Discriminant projection matrix W .
1. Compute the mean of each class i, m
i
and the mean of all the classes m.
2. Construct
ˆ
H
b
,
ˆ
H
w
from (9) and (10).
3. Perform QR decomposition
ˆ
H
b
:
ˆ
H
b
= QR.
4. Compute
˜
S
b
= Q
t
ˆ
S
b
Q and
˜
S
w
= Q
t
ˆ
S
w
Q.
5. Compute the t eigenvectors g
i
of (
˜
S
b
)
−1
˜
S
w
with increasing eigenvalues, where t = rank(
ˆ
H
b
).
The projection matrix is W = QG with G = [g
1
,. . . , g
t
].
sample all images to 56x46 pixels without any other pre-processing. For the test proto-
col we randomly take k images from each class as the training data, with k ∈
{
2,...,9
}
,
and leave the rest 10 −k images as the probe. The Nearest Neighbour algorithm was
employed with Euclidean distance for classification. Such test is run ten times and we
take the average of the results for comparison. At the training phase, we represent each
image by a raster scan vector of the intensity value as the column of the input data
matrix X. Moreover, to choose the value of the parameter h in the weighting function,
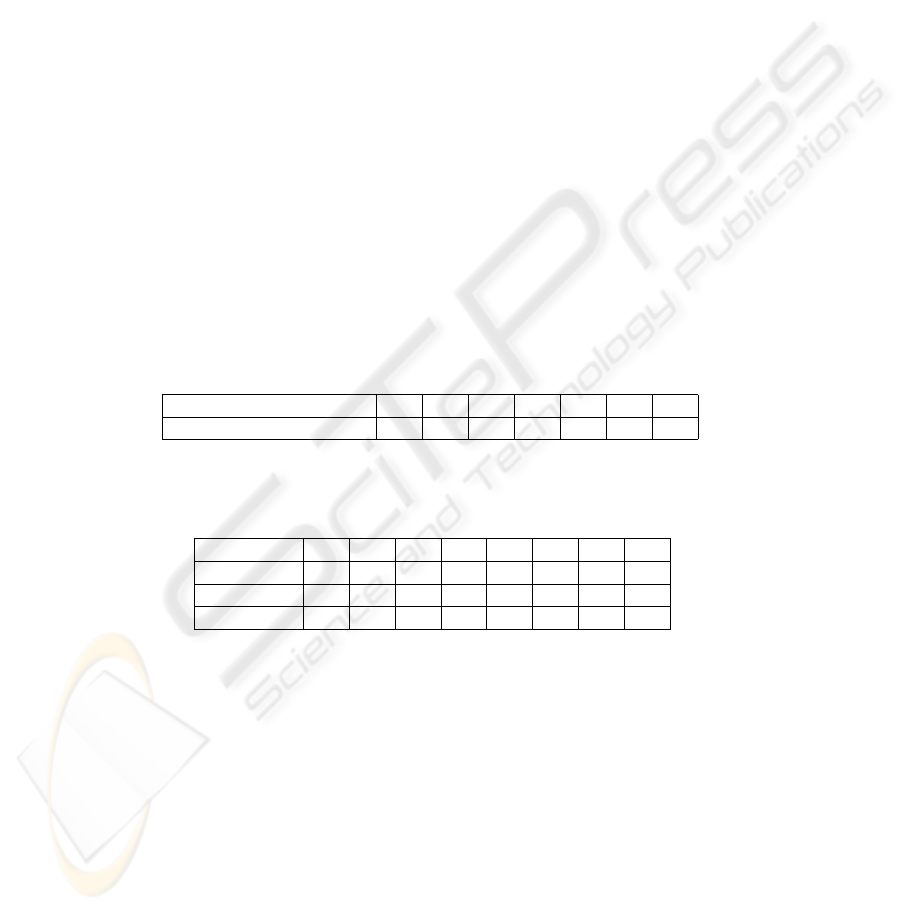
we have calculate the recognition rate with vary within the range from 1 to 7. Table 1
shows the results over the variation of h, from which the value h = 4 achieves the max
recognition rate. Hence, for the rest of paper we take h = 4. Average recognition rate
for each of the three algorithms is reported in Table 2.
Table 1. Recognition rates for different h in RW-LDA/QR.
h 1 2 3 4 5 6 7
Recognition Rates (percent) 81,90 82,20 82,78 83,62 81,46 80,84 80,09
Table 2. Recognition rates (percent)for the ORL dabase.
k 2 3 4 5 6 7 8 9
Fisherface 76,06 86,78 92,95 94,15 95,06 95,75 96,37 97,05
LDA/QR 81,43 90,60 93,20 96,37 96,30 97,50 98,08 99,00
RW-LDA/QR 83,62 92,00 95,20 96,25 97,75 98,91 99,00 99,75
From these results we see that the proposed method RW-LDA/QR performs better
performance. In other word, we present the results using wavelets transform as fea-
ture extraction. Original images used here have a 112x92 size. The columns of the data
matrix are generated by the lowest frequency subimages (LL) from 2D wavelet decom-
position on the original images of database.
Table 3 shows the comparisons result of the algorithms with one-level Haar wavelet
decomposition. Table 4 list the results with Haar wavelets at level 2.
It is noted that there are a weak increase in the Recognition rate for LDA/QR but not
a great change for RW-LDA/QR with the use of the one-level 2D Haar wavelet trans-
form. In addition, one sees in Table 3 that starting from level 2 of the decomposition in
186

Table 3. Recognition rates using one-level 2D Haar wavelet transform.
k 2 3 4 5 6 7 8 9
LDA/QR 81,43 90,60 93,20 96,37 96,30 97,50 98,08 99,00
RW-LDA/QR 83,62 92,00 95,20 96,25 97,75 98,91 99,00 99,75
Table 4. Recognition rates using tow-level 2D Haar wavelet transform.
k 2 3 4 5 6 7 8 9
DWT+LDA/QR 66,56 79,82 86,12 90,40 94,18 95,66 97,00 98,00
DWT+RW-LDA/QR 71,65 82,25 89,12 92,80 95,87 97,16 97,37 98,50
wavelet, the performance of algorithms LDA/QR and RW-LDA/QR are degraded with
superiority for RW-LDA/QR compared to LDA/QR.
Second Group: The Yale face database consists of images from different people,
using 11 images from each person, for a total of 165 images. For simplicity of computa-
tions, we have downsampled the images to 50x50 pixels. Firstly we have performed the
Fisherface, LDA/QR an RW-LDA/QR on Yale database without wavelet features. Sec-
ondely, using two-level 2D Harr wavelet transform we have performed DWT+LDA/QR
and DWT+RW-LDA/QR algorithms. Fig.1 depicts the recognition rate of all algotihms.
Hence, as we can see it on Fig.1, the use of wavelets features improves the performance
of LDA/QR and RW-LDA/QR algorithms, especially on Yale database that contains
images with variations on illumination.
Fig. 1. Recognition rate for yale database.
187

5 Conclusion
In this paper, we presented a novel method for face recognition. Our method outper-
forms others LDA based methods on ORL database and it performs acceptable result
for Yale database. The use of wavelets as feature extraction improves the performance
of the algorithms presented in this paper. However all algorithms presented in this paper
are linear methods. Since facial variations are mostly non linear, LDA, LDA/QR and
RW-LDA/QR projections could only provide suboptimal solutions. On future work we
plan to extend the algorithm presented in this paper by introducing kernel methods to
take account of this drawback.
References
1. S.G.Mallat, ”A theory for multiresolution signal decomposition: the wavelet representation”,
IEEE Tran on Pattern Analysis and Machine Intelligence, vol.11, no.7, pp674-693, Jul.1989.
2. K.Fukunaga, Introduction to Statistical Pattern Recognition, Academic Press, New York,
1990.
3. P.Belhumeur,J.P. Hespanha and D.J.Kriegman, ”Eigenface vs. Fisherface: Recognition using
class specific linear projection” IEEE Trans. on PAMI, vol.17(9),pp.711-720, 1997.
4. D. L. Swets, J. Weng, ”Using discriminant eigenfeatures for image retrieval”, IEEE Trans.
on PAMI, vol 18 (8), pp. 831-836, 1996.
5. J. Ye, Q. Li ”LDA/QR: an efficient and effective dimension reduction algorithm and its the-
oretical foundation” Pattern Recognition, vol. 37(4), pp. 851-854, 2004.
6. M. Loog, R. P.W.Duin, R Hacb-Umbach, ”Multiclass linear dimension reduction by
weighted pairwise Fisher criteria”, IEEE Trans. on PAMI, vol 23, pp.762-766, 2001.
7. R.Rotlikar, R.Kothari, ”Fractional-Step dimentionality reduction ”, IEEE Trans. on PAMI,
vol 22, pp.623-627, 2000.
8. E. K Tang, P. N. Suganthan, X. Yao, A. K. Qin, ”Linear dimensionality reduction using
relevance weighted LDA”, Pattern recognition, vol. 38, pp.485-493, 2005.
9. G. H. Golub, C. F. V. Loan, Matrix Computation, 3rd Edition, the Johns Hopkins University
Press, Baltimore, MD, USA, 1996.
10. ORL.Web.site: http://www.cl.cam.ac.uk/research/DTG/attarchive/
11. Yale.Web.site: http://cvc.yale.edu/projects/yalefaces/yalefaces.html
188
