A Weight Vector Feature for 3D Shape Matching

Yingliang Lu

, Kunihiko Kaneko

and Akifumi Makinouchi

Graduate School of Information Science and Electrical Engineering, Kyushu University

Fukuoka, Japan

Department of Information and Network Engineering, Kurume Institute of Technology

Fukuoka, Japan

Abstract. In the present paper, we introduce a novel segment weight vector to

matching 3D objects rapidly. We split a 3D object into parts according to its

topology, and make up the extracted the thickness feature of each part as a

feature vector of the 3D object. Furthermore, we present a new solution for

improving the accuracy of the similarity queries. Since the proposed method is

based on partial features, it is particularly suited to searching objects having

distinct part structures and is invariant to part architecture.

1 Introduction

Since 3D models are increasingly created and designed using computer graphics,

computer vision, CAD medical imaging, and a variety of other applications, a large

number of 3D models are being shared and offered on the Web. Large databases of

3D models, such as the Princeton Shape Benchmark Database [10], the 3D Cafe

repository [21], and Aim@Shape network [13], are now publicly available. These

datasets are made up of contributions from the CAD community, computer graphic

artists, and the scientific visualization community. The problem of searching for a

specific shape in a large database of 3D models is an important area of research. Text

descriptors associated with 3D shapes can be used to drive the search process [20], as

is the case for 2D images [23]. However, text descriptions may not be available and

may not apply for part-matching or similarity-based matching. Several content-based

3D shape retrieval algorithms have been proposed [3] [4] [5] [8] [19].

For the purpose of content-based 3D object retrieval, various features of 3D

objects have been proposed [1] [5] [8] [19] [9]. However, these features are global

features. That is, they describe the geometry or topology information of a 3D object

using one feature. The shock graph comparison based retrieval method described in a

previous paper [7] is based only on the topologic information of the shape. An

approach based on a new geometric index structure is suggested in [3]. The basic idea

of this solution is to use the concept of hierarchical approximations of the 3D objects

to speed up the search process. However, this is still based on global features. An

efficient geometrical and partial similarity based method is needed to retrieve 3D

objects.

In the present paper, we propose a novel feature vector of a 3D object. This feature

vector is based on geometrical information rather than on topological information

Lu Y., Kaneko K. and Makinouchi A. (2007).

A Weight Vector Feature for 3D Shape Matching.

In Proceedings of the 7th International Workshop on Pattern Recognition in Information Systems, pages 69-78

DOI: 10.5220/0002414700690078

 SciTePress

alone. The vector is herein referred to as the Segment Weight Vector (SWV). The

SWV is more effective and flexible than the Curve-Skeleton Thickness Histogram

(CSTH) [6] on partially based object matching. Furthermore, we propose a novel

method to search similar objects from 3D object database using the feature. We refine

the result with a filter using the Segment Thickness Histogram (STH) of the curve-

skeleton. In our proposal, a number of similar 3D objects are retrieved from a 3D

object model database if the volume features of the parts of the key object are similar

to any part of the potential candidate 3D objects. The similar objects are inserted into

the candidate pool. As an accuracy improvement step, the 3D objects will be removed

from the candidate pool if the CSTH of the processing part of the key object is not

similar to any CSTHs of the potential candidate object. Therefore, the proposed

method can also be easily implemented on other multi-branch complex graph

matching applications if there are different heavy values on the curves.

The remainder of the present paper is organized as follows. Section 2 provides an

overview of research related to skeleton generation and content-based retrieval. In

Section 3, we describe a feature vector (SWV) of 3D objects based on the topology of

their curve-skeletons and partial geometries. In addition, we describe the Segment

Thickness Histogram (STH) of the curve-skeleton. In Section 4, we describe the novel

algorithm and a similar 3D object retrieval method based on the SWVs and STHs, as

mentioned in Section 3, of the 3D object. The performance test results of different

strategies and a discussion thereof are presented in Section 5. Finally, in Section 6, we

conclude the paper and present ideas for future study.

2 Related Work

A number of different approaches have been proposed for the matching problem.

Using a simplified description of a 3D model, usually in one or two dimensions (also

known as a shape signature), the 3D matching can be implemented by comparing

these different signatures. The dimensional reduction and the simple nature of these

shape descriptors make them ideal for applications involving searching in large

databases of 3D models. Osada et al. in [19] proposed the use of a shape distribution,

sampled from one of many shape functions, as the shape signature. Among the shape

functions, the distance between two random points on the surface proved to be the

most effective for retrieving similar shapes. In [24], a shape descriptor based on 2D

views (images rendered from uniformly sampled positions on the viewing sphere),

called the Light Field Descriptor, performed better than descriptors that use the 3D

properties of the object. In [14], Kazhdan et al. propose a shape description based on a

spherical harmonic representation. Kriegel et al. [1] present an approach for

describing voxelized objects. The cover sequence model approximates a voxelized 3D

object using a sequence of grid primitives (called covers), which are basically large

parallelepipeds. Lau et al. [2] surveyed some representative research on 3D model

retrieval, focusing their analysis on feature matching. Existing methods are divided

into three groups: geometry-based, frequency-based, and topology-based.

Unfortunately, these previous methods cannot deal with partial matching. Another

popular approach to shape analysis and matching is based on comparing graph

representations of shape. Nicu et al. [9] developed a many-to-many matching

algorithm to compute shape similarity on the topologic information of the curve-

skeleton. Sundar et al. [5] developed a shape retrieval system based on the skeleton

graph of the shape. These previous methods focus only on the topologic information

of the shape. Unfortunately, the most important shape information (i.e., geometric

information) is neglected. Moreover, using a graph to match shapes is more costly. Lu

et al. [6] proposed a novel shape feature of a 3D model, called the Curve-Skeleton

Thickness Histogram (CSTH). The CSTH is based on the geometric information of

the shape but only describes the matching algorithm of one segment on the curve-

skeleton of a shape model. However, there was no discussion as to how to match two

3D models that have multiple segments on their curve-skeleton.

In [5] [9], curve-skeletons are a 1D subset of the medial surface of a 3D object and

have recently been used in shape similarity matching. A number of algorithms and

applications based on curve-skeletons have developed in the last decade. Topological

thinning methods [15] can directly produce a curve-skeleton that stores the topologic

information of objects. Unfortunately, these algorithms are resolution-dependent and

lose the geometric information of objects. Distance transform methods [12] use the

distance field of volume data to extract the skeleton. Unfortunately, these methods do

not produce a 1D representation directly. Using these methods requires some

significant post-processing. However, some geometric information on the extracted

voxel is maintained.

Various types of fields generated by functions are used to extract curve-skeletons.

They can produce nice curves on medial sheets. The potential at a point interior to the

object is determined as a sum of potentials generated by point charges on the

boundary of the object. Such functions include the electrostatic field function [16] and

the visible repulsive force function [17]. The skeleton points are found by determining

the “sinks” of the field and connecting them using a force following algorithm [11] or

minimizing the energy of an active contour [18], which are used to generate an initial

skeleton in the present paper.

3 Feature Extraction

In this section, we briefly describe the method used to build the thickness of a curve-

skeleton from 3D polygonal models. For details, please refer to Reference [6].

3.1 Skeleton Extraction

A number of methods of skeleton extraction have been reported [11] [12]. The

electrostatic field function [11] can extract well-behaved curves on medial sheets.

Even though the result is connected, the extracted curves are divided into a number of

segments based on electrostatic concentration. However, we need to split the skeleton

into parts based on topology rather than on electrostatic concentration. In Reference

[6], the initial curve-skeleton based on the method in [11] is first extracted. The

distance transform (DT) algorithm [12] was then used to compute the DT of all voxels

on the extracted curve-skeleton (Fig. 2). Finally, in Reference [6], all of the curve-

skeletons of the object were assumed to be connected and to have no branches. Then,

a similarity computation method of 3D object models based on the curve-skeletons

thickness distribution of the entire object model was introduced.

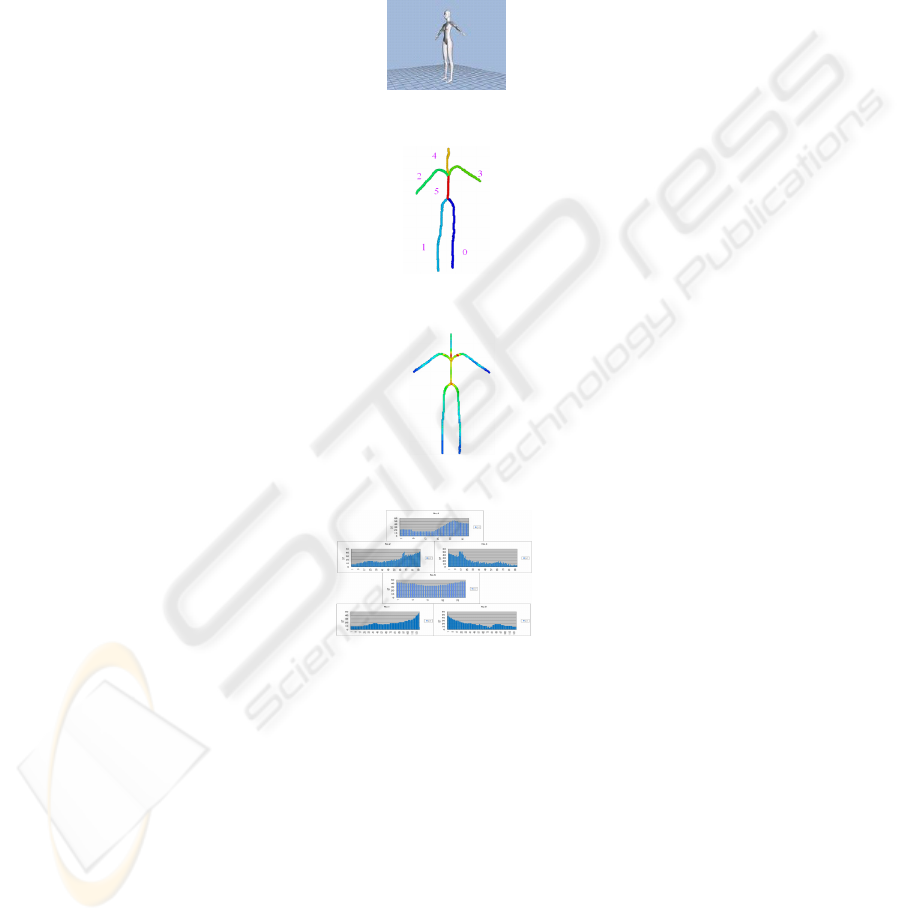
Fig. 1. Three-dimensional model used to extract the skeleton.

Fig. 2. Curve-skeleton with thickness of the 3D model in Fig. 1.

Fig. 3. Segments of the curve-skeleton after splitting the curve-skeleton in Fig. 2.

Generally, there must be several branches on the curve-skeleton of a complex

object (Fig. 1). First, we merge all of the parts separated from the curve-skeleton into

a continuous curve. The continuous curve is then broken into parts according to its

topology (Fig. 3).

3.2 Segment Weight Vector

We herein propose a new partial feature based 3D object feature to represent a part of

a 3D model for similarity measurement. The partial feature of each 3D object is

defined by the volume size of its segment thickness histogram (Fig. 7). We compute

the weight value of all of the parts, which correspond to the segments of the curve-

skeleton. Furthermore, we use these weight values to assemble a vector called the

SWV (as mentioned in Section 1) to represent the global feature of the 3D model.

In order to generate the SWV, we first compute the volume size of each part of

each 3D object using the following formula:

∫

(1)

where

w is the weight of a segment on the curve-skeleton, which represents a

geometrical feature of the part of the corresponding 3D object to which the segment

belongs, and T

represents the thickness of a segment at position x, which indicates

the position of a voxel on the segment.

Second, in order to obtain a SWV representation that is invariant with the order of

the 3D model parts for similarity matching, a sorting step is needed. We sort the

weight of parts of a 3D object by descent. The sorted values make up the SWV of a

3D object.

SWV =

),,,(

110 −n

www L

(2)

where

w represents the weight of the i-th segment, and

110 −

≥≥≥

www L .

Therefore, in order to obtain an SWV that is invariant with the scale of a 3D model

for similarity matching, a normalization step is needed. We normalize the vector by

its maximum value, as follows:

/ www

(3)

where i represents the index of

w in a sorted SWV, and

110 −

≥≥≥

www L ,

]1,1[ −∈ ni

. The normalized and sorted SWV is denoted as SWV ,

),,,,1(

−

wwwSWV L .

(4)

3.3 Normalization of the Segment Thickness

In order to obtain the Segment Thickness Histogram (STH) representation that is

invariant with the scale of a 3D model for similarity measurement, a normalization

step is needed. The horizontal axis of the distribution should be normalized with a

fixed value. Moreover, the vertical axis should be zoomed by a ratio that is equal to

the zoom ratio of horizontal normalization. Using the normalization strategy, we use

the variation of each STH of the object as a feature of the object. Furthermore, in this

method, we treat the proportion of the length of a segment and the thickness

distribution along with the segment as a component of the feature.

4 Searching Algorithm

After the SWVs of the 3D models are constructed, we need a dissimilarity measure in

order to compare two 3D models. In this section, we describe how to compare two

SWVs and how to retrieve 3D objects from a database by their partial geometrical

features.

In our implementation, we have performed an experiment using a simple

dissimilarity measure based on the L

norms function with n = 2. We used the

following formula:

()

issimilarity X Y=−

∑

(5)

where X

and Y

represent the i-th elements in two SWVs.

Our main idea is based on the fact that two objects are similar if all of their

corresponding parts are geometrically similar. Thus, if the volumes and thicknesses

the histograms of two 3D objects are similar for each segment of their curve-skeletons,

then the two 3D objects may be similar.

However, the similar segment thickness histograms retrieval is a multidimensional

database problem. We developed a new algorithm to improve the retrieval

performance. First, we find 3D models from the database by matching the SWVs.

Therefore, we need to use a similar object retrieval strategy that uses STHs to

improve the retrieval accuracy.

In order to retrieve the most similar objects, we first sort the 3D objects by their

SWV similarity. In our implementation, we retrieve only the 3D objects of which the

total numbers of segments (number of elements in their SWVs) are the same. We then

sort the retrieved result set based on the similarity of their SWVs and select only the

top m objects for the next step.

Second, we use STHs of the selected 3D objects to improve the accuracy of the

retrievals. We retrieve the most similar n segments from the selected 3D object set.

This 3D object set includes only the m objects output in the first step. In addition,

each of the n retrieved segments belongs to different 3D objects. The retrieved result

is shown in Table 1. In the table, KS indicates the key object with an m-segment

curve-skeleton, and KS.SG

is the segment that has the largest STH volume. In

addition, CS

.SG

indicates that the segment SG

is on the curve-skeleton of the CS

object. Finally, the most similar 3D objects are found from Table 1 using SQL. The

3D objects having the largest number of similar segments are reported as the result of

3D object retrieval. In addition, the final step is to find the 3D objects that they have

the most amounts in the candidate pool of Table 1.

Table 1. Candidate pool of the key object.

Key Candidate pool

KS.SG

.SG

⋯

.SG

KS.SG

.SG

⋯

.SG

⋮ ⋮ ⋮ ⋮

KS.SG

.SG

⋯

.SG

5 Experiment and Discussion

In order to test the proposed feasibility of the similar object retrieval strategy, we

implement the present algorithms on a Linux system by C++ and PostgreSQL. We set

the resolution of the volume data as

200200200

in the volume voxelization

procedure. We used the Princeton shape database [10] as the test data in the present

study. We found that the proposed method works well for similar object retrieval

based on the geometrical feature of partial bodies.

Although there are 1,814 3D objects in the Princeton shape database, we only

generated 1,453 curve-skeletons of 1,453 3D models from the database because the

skeleton-making algorithm cannot generate a curve-skeleton from some 3D models.

In addition, the generated 1,453 curve-skeletons include 51,952 segments in our test

database.

The key object (Fig. 4) of test has six segments on its curve-skeleton (Fig. 5).

These segments belong to a head (number of segments: 4), a trunk of a body (number

of segments: 5), and four limbs (numbers of segments: 0, 1, 2, and 3). Since each

segment has its own thickness histogram, the key object has six independent thickness

histograms (Fig. 7).

Fig. 4. Key model used to search the 3D model database.

Fig. 5. Segment number of the curve-skeleton of the key model in Fig. 4.

Fig. 6. Curve-skeleton with thickness of the key model in Fig. 4.

Fig. 7. Thickness distribution graph on the segments of the curve-skeleton of the key model in

Fig. 4.

In order to test the feasibility of the similar object retrieval strategy proposed

herein, we implement the proposed algorithms in two ways.

First, we test the similar object retrieval strategy only by STHs. The results are shown

in Fig. 8. In addition, in order to find no more than 30 objects using a segment of a

key object (Fig. 4), we set the parameter n (number of maximum retrieval results) as

30 for the experiments. Our filtering program retrieves 30 objects by each STH of the

key object and then inserts these objects into the temporary table. In order to find the

objects of which the STHs match the key object for the head, the trunk of the body,

and the four limbs, we need to find the best objects from each result set of the six

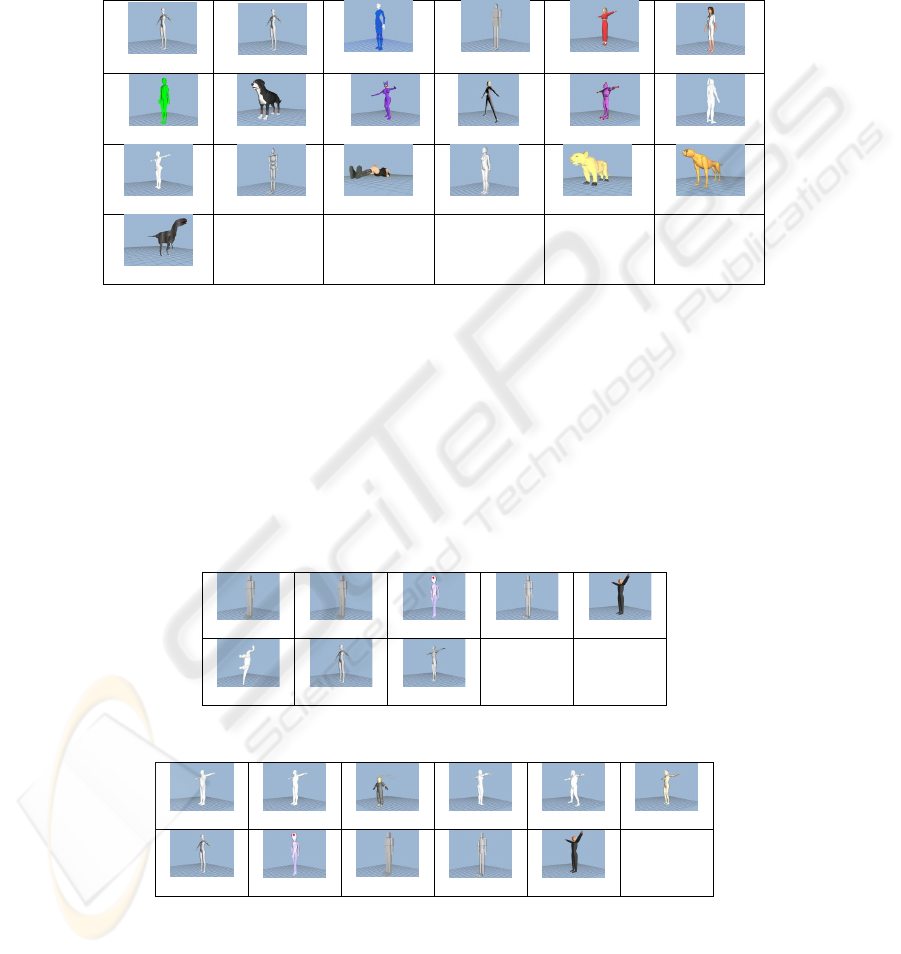
parts. We obtain eighteen objects in which each of the six key parts has a matching

part. Figure 8 shows a number of result objects of the object retrieval test and reveals

that the proposed method can find similar objects and retrieve the models that have

parts that are similar to the key object (e.g., result 7 in Fig. 8). The part of the tail of

result 7 does not have a part that is similar to the key object, and therefore cannot be

reported based on global features.

Key

Result 1

Result 2 Result 3 Result 4

Result 5

Result6 Result 7 Result 8 Result 9 Result 10 Result11

Result 12 Result 13 Result 14 Result 15 Result 16 Result17

Result 18

Fig. 8. Results of retrieval by the dissimilarity of the Segment Thickness Histograms only.

We test the similar object retrieval by partial geometry. In addition, we retrieve 3D

objects from a database using their SWV similarity. Furthermore, we use the STH

similarity to improve the retrieval accuracy. The results retrieved by different keys are

shown in Figs. 9 and 10.

Finally, we also compare the retrieval performance of the two methods mentioned

above. We test the retrieval performance by the different key objects (m221, m202,

m213, m224, m233, m258 in the Princeton shape database). The result, shown in Fig.

11, indicates that the second method can be used to more quickly obtain the result set.

In addition, the second method can retrieve a more accurate result set from the test

database.

Key Result 1 Result 2 Result 3 Result 4

Result 5 Result 6 Result 7

Fig. 9. Results of retrieval by the dissimilarity of Segment Weight Vector initially.

Key

Result 1 Result 2 Result 3 Result 4

Result5

Result 6

Result 7

Result 8

Result 9 Result 10

Fig. 10. Results of retrieval by the dissimilarity of Segment Weight Vector initially.

Fig. 11. Retrieval performance comparison of the two methods mentioned above.

6 Conclusions and Future Studies

We novel proposed a partial feature named SWV to retrieve 3D model by their partial

similarity. In addition, the 3D object retrieval method proposed in the present paper is

based on partial geometry similarity between 3D objects. First, the proposed method

extracts a curve-skeleton with thickness. Second, we compute the dissimilarity of the

SWV (mentioned in Section 1) and propose a novel 3D object retrieval strategy using

the computed dissimilarity. Third, we compute the dissimilarity of the Segment

Thickness Histograms (STHs) of each part with respect to the objects. Finally, we use

the dissimilarity of STHs to improve the accuracy of the retrieval. It is possible to

effectively retrieve 3D models by partial similarity in the present experiments.

Since these SWVs and STHs are extracted from 3D objects using the geometrical

information of a 3D object, the 3D objects can be compared based on geometrical

information rather than on topologic information alone. Since each of the elements of

the SWV and the STH are a partial feature of a 3D object, both the SWV and the STH

can compare two 3D objects based on their partial features, rather than on their global

features alone. Good efficiency and good results were obtained in the present

experiments using the proposed method.

References

1. Hans-Peter Kriegel , Stefan Brecheisen , Peer Kröger , Martin Pfeifle , Matthias Schubert,

Using sets of feature vectors for similarity search on voxelized CAD objects, Proceedings

of the 2003 ACM SIGMOD international conference on Management of data, June 09-12,

2003, San Diego, California.

2. R.W.H. Lau and B. Wong, “Web-Based 3D Geometry Model Retrieval,” World Wide Web

Journal, Kluwer Academic Publishers, 5(3):193-206, 2002.

3. D. Keim. “Efficient Geometry-based Similarity Search of 3D Spatial Databases”. In Proc.

ACM SIGMOD Int. Conf. on Management of Data (SIGMOD'99), Philadelphia, PA, pages

419-430, 1999.

4. F. Korn, N. Sidiropoulos, C. Faloutsos, E. Siegel, and Z. Protopapas. “Fast Nearest

Neighbor Search in Medical Image Databases”. In Proc. 22th Int. Conf. on Very Large

Databases (VLDB'96), pages 215-226, 1996.

5. H. Sundar, D. Silver, N. Gagvani, and S. Dickenson: Skeleton based shape matching and

retrieval SMI 2003, pages 130-139,2003

6. Y. Lu, K. Kaneko and A. Makinouchi: 3D Shape Matching Using Curve-Skeletons with

Thickness, 1st Int. Workshop on Shapes and Semantics, June 2006

7. K. Siddiqi, A. Shokoufandeh, S. Dickinson, and S. Zucker: Shock graphs and shape

matching International Journal of Computer Vision, 30:1-24,1999

8. M. Hilaga, Y. Shinagawa, T. Kohmura, and T. Kunii: Topology Matching for Fully

Automatic Similarity Estimation of 3D Shapes ACM SIGGRAPH 2001 Proceedings, 2001

9. Nicu D. Cornea, M. Fatih Demirci, Deborah Silver, Ali Shokoufandeh, Sven J. Dickinson,

Paul B. Kantor: 3D Object Retrieval using Many-to-many Matching of Curve Skeletons

International Conference on Shape Modeling and Applications SMI 2005. MIT, Boston,

MA. June 15-17,2005

10. P. Shilane, M. K. P. Min, and T. Funkhouser: The princeton shape benchmark Shape

Modeling International, Genoa, Italy, June, 2004

11. N. Cornea, D. Silver, X. Yuan, R. Balasubramanian: Computing Hierarchical Curve-

Skeletons of 3D Objects The Visual Computer, Vol. 21, No. 11, pp. 945-955,2005

12. N. Gagvani and D. Silver: Parameter controlled volume thinning Graphical Models and

Image Processing, 61(3): 149-164,1999

13. AIM@SHAPE Network of Excellence, ( http://www.aimatshape.net/ ).

14. M. Kazhdan, T. Funkhouser, and S. Rusinkiewicz: Rotation invariant spherical harmonic

representation of 3d shape descriptors In Symposium on Geometry Processing, pages 167-

175,2003

15. Toyofumi Saito, Satoshi Banjo and Jun-ichiro Toriwaki: An improvement of three

dimensional thinning method using a skeleton based on the Euclidean distance

transformation - a method to control spurious branches, IEICE Trans. on Inf. and Syst.,

Japan, J84-D-II, 8, pp.1628-1635 (2001.8)

16. T. Grigorishin, Y.H. Yang. Skeletonization: An Electrostatic Field-Based Approach Pattern

Analysis and App., 1:163-177,1998

17. F. Wu, W. Ma, P. Liou, R. Liang, M. Ouhyoung: Skeleton Extraction of 3D Objects with

Visible Repulsive Force Eurographics Symp. On Geometry Processing, 2003

18. W. Ma, F. Wu, M. Ouhyoung: Skeleton Extraction of 3D Objects with Radial Basis

Functions IEEE SMA, 2003.

19. R. Osada, T. Funkhouser, B. Chazelle, and D. Dobkin: Matching 3D Models with Shape

Distributions Shape Modeling International, Genova, Italy, May,2001

20. Princeton Shape Retrieval and Analysis: 3D Model Search

http://shape.cs.princeton.edu/search.html

21. 3D Cafe: http://www.3dcafe.com/asp/freestuff.asp

23. Google Image Search: http://www.google.com/

24. Chen, D.Y., Ouhyoung, M., Tian, X.P., Shen, Y.T., Ouhyoung, M.: On visual similarity

based 3D model retrieval. In: Proc. Eurographics, Granada, Spain (2003)