ANALYSIS OF BUSINESS PROCESS FLEXIBILITY AT

DIFFERENT LEVELS OF ABSTRACTION

Marite Kirikova, Renate Strazdina, Janis Grundspenkis

Department of Systems Theory and Design, Riga Technical University, Latvia

Janis Osis

Department of Applied Computer Sciences,, Riga Technical University, Latvia

Keywords: Business process, topological functioning model, cycle analysis, flexibility.

Abstract: Business process flexibility is understood as capability of the process to be changed without replacing it

completely. This implies that there should be one part of the process that may be changed and another part

of the process (process core) that should not be changed. The challenge of business process analysis is the

detection and separation of these process subparts. One of the possible ways to meet this challenge is

through use of topological functional modeling and utilization of graph theory methods, such as paths and

cycle detection in a digraph at different levels of abstraction. The cycles that are found at several levels of

abstraction may help detecting the core of the business process while other cycles may point to the

changeable parts of the process.

1 INTRODUCTION

Today’s organizations are generally operating in an

increasingly turbulent environment (Cao et al.,

2003). Business process flexibility is one of the

possible responses to the challenges posed by these

conditions. For instance, organizational theory views

individual modern organizations as members of an

inter-organizational network (Hatch, 1997); hence,

changes occurring in other network members may

require a matching adjustment in the particular

organization. Such adjustments may affect various

sub-systems of the organization, say, goals sub-

system, process sub-system, structure or resource

sub-systems (Sprice and Kirikova, 2005). The focus

of this paper is on business processes adjustments.

We will examine this topic from a process flexibility

point of view.

For the purposes of this paper flexibility will be

defined as the ability to attain the stated results of a

business process even where the environment in

which the business process is occurring has changed.

At the same time there are constraints on how

flexible a particular business process may become

before it turns into an entirely different one (Regev

et al., 2006). From a systems theory point of view a

flexible business process features feedback

capability ensuring that when the process result

differs from what is expected due to changes in the

environment, the process is adjusted until the

expected result is attained. In this paper we will

apply topological functional modeling for analysis

of business process flexibility at different levels of

abstractions. The purpose of this analysis is to reveal

the most important part of the process which may

constitute the non-changeable core. Identification of

process core could provide means for effective

decision making with respect to enterprise

information systems development.

The paper is structured as follows: Section 2

briefly illustrates the state of the art in business

process flexibility analysis performed by different

researchers; in Section 3 the basics of topological

functioning model development and cycle oriented

interpretation of flexibility are discussed; in Section

4 the approach discussed in Section 3 is applied to a

business sub-process analysis at different levels of

abstraction (the application is illustrated by a small

industrial example); and in Section 5 we discuss

implications of our approach to enterprise

389

Kirikova M., Strazdina R., Grundspenkis J. and Osis J. (2007).

ANALYSIS OF BUSINESS PROCESS FLEXIBILITY AT DIFFERENT LEVELS OF ABSTRACTION.

In Proceedings of the Ninth International Conference on Enterprise Information Systems, pages 389-396

 SciTePress

information systems development and point to

intended further research questions.

2 THE ISSUE OF BUSINESS

PROCESS FLEXIBILITY

The main purpose of every information system is

supporting a range of particular business processes.

As business processes should be capable of adjusting

reasonably swiftly to changes in the external

environment, such processes ought to, by definition,

be flexible (Regev et al., 2006). That also means that

if an information system is to support specific

business processes continuously it should be flexible

as well. Developing flexible information systems has

been the subject of extensive research (Daoudi and

Nurcan, 2006); however, an unambiguous definition

of a flexible business process has not been provided

so far. As a consequence, developing information

systems supporting such processes is a non-trivial

task.

There are different definitions of flexibility;

however most of them focus on the ability to

respond to external changes in an appropriate period

of time using a reasonable amount of resources

(Regev et al.,(2006), Daoudi and Nurcan, (2006),

(Snowdon, et al., (2006)). For instance, according to

Regev (Regev et al., 2006), since flexibility is the

capability to change, it can be classified with respect

to the types of changes it enables. Snowdon et al.

(Snowdon, et al., 2006) writes that flexibility is the

‘ability of a firm’s processes and systems to respond

quickly to changes in the business environment. It

includes the capacity to accommodate shifts in

consumer demand, in competitors’ strategies, in rate

of growth, and in suppliers’ deals and shipment

problems’.

Even so, the meaning of the term ‘flexibility’

varies from research to research. A taxonomy of

business process flexibility has been developed in an

attempt to decrease this ambiguity (Regev et al.,

2006). The taxonomy includes three dimensions:

The abstraction level of change (business process

type and process instances); the subject of change

(functional perspective, operational perspective,

behavioral perspective, informational perspective,

organizational perspective); and the properties of

change (the extent, the duration, the swiftness and

the anticipation of change). On the other hand there

are authors who believe business process flexibility

can be examined from three points of view that

differ from those listed in Regev’s (Regev et al.,

2006) taxonomy: Characteristics of the stimulus that

generates the requirements for business process

flexibility; business process flexibility itself; and the

strategies and tactics employed to achieve business

process flexibility (Regev et al., 2006). Snowdon et

al. (Snowdon, et al., 2006) defines that flexibility

can be categorized in terms of three factors: Type of

flexibility (arising from the variety of different

information types); volume flexibility (arising from

the amount of information types to be dealt with);

and structural flexibility (arising from the need to

operate in different ways).

Summarizing the different approaches described

above we come to the conclusion that business

process flexibility should be considered from two

aspects: The external dimension containing factors

that define the necessity for such flexibility and the

need to apply it; and the internal dimension which

defines the subject of change, the extent of change,

and the strategy for achieving such changes.

Several researchers (Regev et al., (2006),

Snowdon, et al., (2006), Kumar and Narasipuram,

2006)) conclude that business process changes may

be related to the structure of the particular process,

data processed, resources and technologies used, and

legal aspects.

An analysis was carried out by other authors on

the extent of change with the following results:

Business process flexibility suffers from the

dilemma that whenever some part of a process is

made flexible, some other part is made inflexible

(Regev and Wegmann, 2006). The key point to

flexibility, therefore, is to know when and what to

change and when and what not to change (Regev

and Wegmann, 2006).

The purpose of our paper is to contribute to

better understanding of the abovementioned

dilemma and to solve the problem of identification

of that part of business process which “is not to be

changed” (Regev and Wegmann, 2006).

3 THE ISSUE OF BUSINESS

PROCESS FLEXIBILITY

As it was discussed in the previous section, the key

point to flexibility is to know when and what to

change and when and what not to change (Regev

and Wegmann, 2006). At the moment there are no

other suggestions how to resolve this dilemma than

agreeing on this issue by using some consensus-

building methods, for instance Enterprise

Knowledge Development method (Bubenko, et al.,

ICEIS 2007 - International Conference on Enterprise Information Systems

390

(2001), Kirikova, (2000)). However, due to the fact

that such decisions have an effect not only on the

strategic level of the enterprise but indirectly pose

requirements for changes in enterprise information

systems it is necessary to find more formal

approaches of flexibility analysis to check the

impact of strategic level decisions on the business

processes and hence to the enterprise information

systems development. Further in this paper we

present our first findings in an attempt to apply

topological functional modeling to analysis of

business process flexibility with the purpose to

detect core (non-changeable) and changeable parts

of business processes under consideration.

Topological Functioning Model (TFM) can be

viewed as a business model that abstracts details

which are abundantly specific for the given

viewpoint. A TFM is an expressive and powerful

instrument for clear presentation and formal analysis

of system operating and an environment the system

operates within.

The TFM has a rigorous mathematical

foundation. It is represented in the form of a

topological space (X, Θ), where X is a finite set of

functional features of the system under

consideration, and Θ is a topology that satisfies the

axioms of topological structures and is represented

in the form of a directed graph. A necessary

condition for topological space construction is a

meaningful and exhaustive verbal, graphical, or

mathematical system description. The adequacy of

the model describing functioning of a particular

system can be achieved by analyzing the

mathematical properties of such an abstract object

(Osis, (1969), Osis, (2006)).

A TFM has topological (connectedness, closure,

neighborhood, and continuous mapping) and

functional (cause-effect relations, cycle structure,

and inputs and outputs) characteristics. In

accordance with systems theory every business and

technical system is a subsystem of the environment.

Besides that the common thing for all systems’

(technical, business, or biological) operations should

be the main feedback which can be visualized as an

oriented cycle. Therefore, it is stated that at least one

directed closed loop must be present in every

topological model of system functioning. It

visualizes the “main” functionality that has vital

importance for the system life. Usually it is even an

expanded hierarchy of cycles. Therefore, proper

cycle analysis is necessary in a TFM construction

because it makes thorough analysis of system

operations and communication with the environment

possible.

On the other hand, from the point of view of

systems theory process P is a set of related activities

that transforms particular inputs I into particular

outputs Y, to achieve a particular objective O

(Skyttner, 1996). When the process under the

consideration is a business process (BP) the

objective O may be expressed in terms of process

BP business mission. Business mission of a process

is the reason why the process exists, i.e. the reason

why the process is beneficial for other processes.

This means that synergy between input given by the

external process and capability of the BP under

consideration brings a particular value to the

external process and to the BP. The value generated

by a repeatable BP must be substantial enough to

ensure its ability to function, i.e. to attract inputs I

and to provide corresponding outputs Y more than

once. Thus each situation when Y produced by BP is

such that it can cause new instance of I to arrive at

the “gates” of BP is considered a productive output

of BP. We will call the moment of this arrival an

external return of instance i (Figure 1). An example

of such return could be a satisfied customer coming

back to the barber’s shop, as well as customer

appearance causing the arrival of another person.

The main cycles (or hierarchy of cycles) in TMF are

those that point to the activities that ensure the

capability of the business process to handle and

cause external returns of input instances.

The issue of flexibility of business process arises

when it permits handling of inputs where at least one

input instance is different concerning at least one

property relevant to the process. The process is

considered flexible if it can handle input instances

that are not ideal with respect to the basic value

creating method(s) of BP (see the bold path – the

sequence of arcs and nodes of the digraph, in Figure

1). This means that the process has at least one

extension that helps to not lose a non-ideal instance

of input without providing value for it (see cycles –

closed sequences of arcs and nodes, in Figure 1). A

well known example of such extension is a

procedure of repeated examination in the university

process that gives another chance to students to

enrich their knowledge. Thus internal return of

instances may help to yield external return of

instances. However, if a process is too busy with its

extensions it may be a sign that either there is a need

to switch to a different method of value creation

where a currently non-ideal instance is considered as

ideal or discover the reasons of wrong proportion

between ideal and non ideal input instances.

ANALYSIS OF BUSINESS PROCESS FLEXIBILITY AT DIFFERENT LEVELS OF ABSTRACTION

391

Figure 1: External and internal return of input instances.

It is essential to understand that the visibility of

paths and cycles in the digraph depends on the level

of abstraction and detail of systems analysis, as well

as on the subsystems chosen for consideration. For

instance, in Figure 1 the main method of value

creation is depicted by the path; however, when

changing the viewpoint of consideration, this path

would be seen as a constituent of the main cycle of a

particular business process BP. To investigate the

applicability of TMF for business process flexibility

analysis a field experiment was performed using

business process models developed for an

international telecommunications company. Part of

the experiment is briefly discussed in the next

section.

4 THE ISSUE OF BUSINESS

PROCESS FLEXIBILITY

For TMF to be suitable for business process

flexibility analysis it should detect the same main

cycle(s) at different levels of abstraction. We

experimented at two levels of abstraction. At the

higher level of abstraction only a story about a small

sub-process told by a practitioner was used. On the

lower level of abstraction the business process

model of the same sub-process was utilized.

Modeling at each abstraction level is discussed in

Sections 4.1 and 4.2 accordingly. A comparison of

modeling results is given in Section 4.3.

4.1 Topological Modeling on the Basis

of the Process Description

At the higher level of abstraction the TFM of the

sub-process receiving data from a multitude of

sources and running a validity check on such data

(see Figure 2a) was analyzed without imposing any

predefined analysis framework on it. The analysis is

described in Subsections 4.1.1-3.

4.1.1 Definition of Functional

Characteristics

At the higher level of abstraction the first step on

TFM construction is the definition of functional

characteristics of the process. In our experiment the

definition was based on word analysis and consisted

of the following activities (Asnina and Osis, 2006):

(1) Definition of objects and their properties from

the problem domain description that is performed by

noun analysis, i.e. by establishing meaningful nouns

and their direct objects as handling synonyms and

homonyms; (2) Identification of external systems

(objects that are not subordinated to the system

rules) and partially-dependent systems (objects that

are partially subordinated to the system rules, e.g.

system workers’ roles); and (3) Definition of

functional features performed by verb analysis in the

problem domain description, i.e. by identifying

meaningful verbs.

In the sub-process description (Figure 2a) nouns

are shown in italic, verbs are shown in bold, and

action pre- (or post-) conditions are underlined. The

identified objects (or concepts) are as follows: (1)

internal objects: the process (synonym: entire

process), a script, a human operator (synonym:

operator), the information transfer, the data

download activity, (data) entirety, data validation

(synonym: validation), the full set of data,

consistency, contents, a manual download process,

the possibility, an automated process, a manual one

(process); (2) external objects – input objects:

process; data at the locations (synonyms are: input

data from certain sources, each input data location,

all the input data, the downloaded data, such input

data storage locations), data stored in an external

system; (3) external object – output object: result –

data matching in all locations.

…

External

return of the

instance

Internal

return of the

instance

ICEIS 2007 - International Conference on Enterprise Information Systems

392

Functional features identified from the fragment

are the following (given in the form: action, object,

(condition), and responsible entity):

1. Commencing the process by the script; 2.

Entering of data at the locations; 3. Collecting data

from the locations by the script; 4. Checking

downloading of data at all locations by the script; 5.

Checking completeness of data at the locations by a

human operator; 6. Re-launching data download by

the human operator; 7. Receiving the full set of data

by the human operator; 8. Commencing validation

by a script; 9. Entering of data stored in an external

system by the script; 10. Downloading of data stored

in an external system by the script; 11. Checking

data at the locations with data stored in an external

system for consistency by the script; 12. Checking

data at the locations with data stored in an external

system for contents by the script; 13. Establishing of

a mismatch by the script; 14.Starting a manual

download process for data at the locations with

mismatch by the human operator; 15. Repeating the

download process for data at the locations with

mismatch by the human operator; 16. Checking the

result – data matching in all locations by the human

operator.

4.1.2 Introduction of the Topology

Introduction of topology Θ is the next step. This

means establishing of cause and effect relations

between functional features. Cause-and-effect

relations are represented as arcs of a digraph that are

orientated from a cause node to an effect node. The

main properties of cause-and-effect relations are the

following: a) a cause chronologically precedes an

effect; b) a cause can be sufficient or necessary

(complete or partial, correspondingly); it is assumed

that there are necessary causes in the topological

functioning model because risks of the system

functioning can be unknown during the analysis; c) a

cause not only precedes an effect and always is

followed by it, it causes and is condition on an

effect; d) the causality is universal, i.e. it exists in

any problem domain even if it is not evident for a

human. A structure of cause-and-effect relations can

form a causal chain wherein each relation is

important.

The cause-and-effect relations between the

functional features identified from the sub-process

description are illustrated by means of the TFM in

Figure 2b.

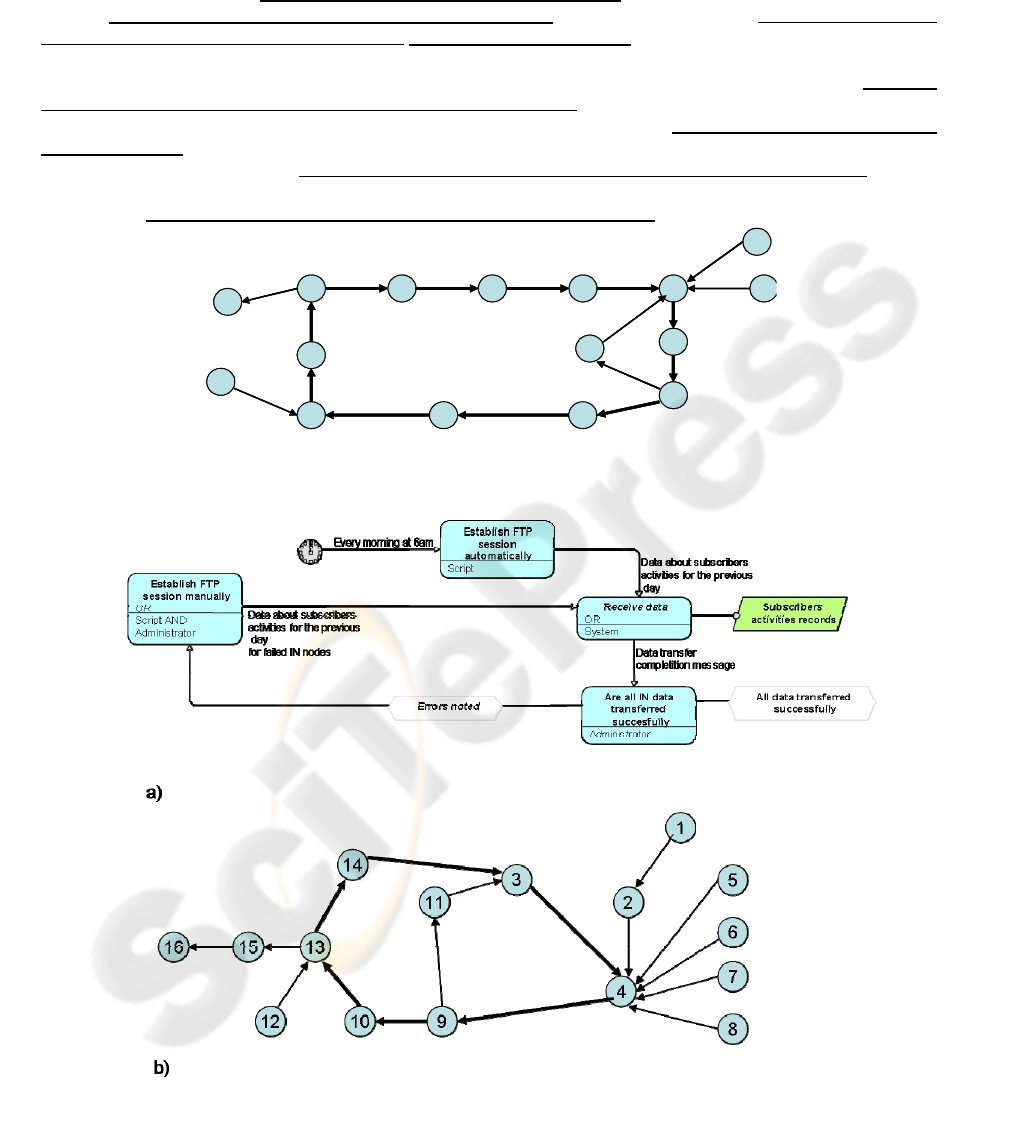
Figure 2b clearly shows that cause-and-effect

relations form functioning cycles. All cycles and

subcycles should be carefully analyzed in order to

completely identify existing functionality of the

system. The main cycle of system functioning (i.e.

functionality that is vitally necessary for system life)

must be found and analyzed before starting further

analysis. In the example, the main functional cycle is

defined by the expert, and includes the following

functional features “3, 4, 5, 7, 8, 10, 11, 12, 13, 14,

15, 3” (bold lines in Figure 2b). As an example of

the first order sub-cycle is a cycle that includes the

functional features “3, 4, 5, 6, 3”.

4.2 Business Process Model in

GRAPES BM

In the approach demonstrated in the previous section

there was no clear separation between such issues as

data, activity, and performer. At the lower level of

business process analysis we used business process

representation in the business process modelling

language GRAPES BM (Kalnins, 1996) which

provides clear separation of mentioned issues. The

business process model fragment in GRAPES BM

corresponding to the description given in Figure 2a

was cut out of the larger process model for the

purposes of the experiment. A small part of this

fragment is shown in Figure 3a.

The GRAPES BM business process model

shows the cause-and-effect relationships between the

tasks of business process to be performed. Thus the

digraph corresponding to the business process model

was obtained by following the inputs and outputs of

the tasks and task-triggering conditions in the

business process model. No distinction was made

with respect to the contents of the information flows.

All of them were considered as a flow of one

substance (Grundspenkis, 1983). The digraph

obtained by reflecting tasks as nodes of the digraph

and information flows as links between them is

reflected in Figure 3b. The graph contains the main

cycle of systems functioning consisting of nodes “3,

4, 9, 10, 13, 14, 3”, and contains a sub-cycle “3, 4, 9,

11, 3”. Note: the numbers of nodes in digraphs

reflected in Figure 2b and Figure 3b do not

correspond each to other, because the graphs were

made by different researchers and granularity of

knowledge about the system reflected in each node

differs considerably from one approach to another.

ANALYSIS OF BUSINESS PROCESS FLEXIBILITY AT DIFFERENT LEVELS OF ABSTRACTION

393

The process commences when a script is launched at a pre-defined time collecting input data from a certain set of

sources. Once the script has downloaded data from al the locations

, a human operator checks whether the information

transfer was complete for each input data location. If it turns out to be incomplete the data download activity is re-launched

manually as many times as is necessary for the operator to verify that all the input data have been received in their entirety.

This verification cycle is the most important component of the process as data validation cannot be commenced unless the

full set of data is received. Once all the input data has been downloaded, validation checks commence. The downloaded

data is checked for consistency and contents with data stored in an external system. In case the data do not coincide in

those two locations a manual download process is repeated for such input data storage locations where a mismatch is

identified. The process terminates when the downloaded data and the data stored in the external system coincide.

Flexibility

of the process is manifested through the possibility of changing an automated process into a manual one and repeating the

entire process if the expected result – data matching in all locations – is not achieved.

Figure 2: Topological modeling at a high level of abstraction: a) source text; b) TFM.

Figure 3: Modeling at abstraction level prescribed by GRAPES BM: a) part of the business process model fragment in

GRAPES BM, b) obtained TMF.

12 13 14 15 3

810

12 13 14 15 3

810

ICEIS 2007 - International Conference on Enterprise Information Systems

394

4.3 Comparison of Modeling Results

The main result of the experiment is that at both

levels of abstraction the main cycle and the sub-

cycle of systems functioning were found.

Theoretically the number of cycles at the lower level

of abstraction could exceed the number of cycles at

higher level of abstraction because, in general, it

shows the business process at a higher level of

detail. In our case the number of cycles was the

same, probably because only a very small fragment

of the business process model was considered. The

meaning correspondence analysis of nodes in Figure

2b and Figure 3b was done to indicate whether both

graphs refer to the same main cycle with respect to

reality. The analysis confirmed that in both graphs

the same main functionality of the business sub-

process under the consideration was found.

The obtained results allow drawing a

hypothesis that TMF at a higher level of abstraction

may be used as a tool for detecting the unchangeable

core of the process. The paths and the cycles that are

outside the main cycle may be analyzed and

designed to achieve the desired level of flexibility.

The sub-process discussed in Sections 4.1 and

4.2 is a flexibility provider for the system in a larger

context containing the script which sometimes

succeeds to get complete and correct information

and sometimes does not. The business value of the

sub-process is to provide trust for the script so that it

could be useful for other processes in a larger

systems context. All nodes of the main cycles are

needed to provide the trust. If we wish to analyze the

flexibility of the sub-process itself, the structure of

the graph related to the main cycle must be

considered and a deeper level of detail chosen for

the nodes of the main cycle. This type of analysis is

beyond the scope of this paper.

4 CONCLUSIONS

Possibility to identify the core processes in a

business process model provides considerable

opportunities with respect to enterprise information

system development. Some of them are as follows:

• Reliability and security issues of core processes

support may be considered at a higher level of

detail than for non-core processes.

• Core processes may be considered as a high

priority candidates in requirements prioritization.

• Different development methods can be used for

core and non-core processes, e.g. more rigid

methods for core processes and more agile ones

for non-core processes.

• Not just business but also software core

processes may be taken into consideration in

making enterprise information systems

development decisions.

One of the ways to determine which tasks or sub-

processes belong to the core of the business process

is through use of topological functioning model

development at different levels of abstraction. The

first steps of application of this approach show that it

promises tangible results. However this modeling

exercise involves a considerable amount of human

knowledge and effort, therefore supporting tools

such as business process model transformation to a

digraph, digraph comparison methods for digraphs

with different level of node granularity, digraph

analysis methods taking into consideration several

business input substances, business process

visualization tools as well as appropriate consensus

building methods could be useful in further

development of the approach.

REFERENCES

Asnina, E., Osis, J., 2006. The Computation Independent

Viewpoint: A Formal Method of Topological

Functioning Model Construction. In: Scientific

Proceedings of Riga Technical University, Series –

Computer Science (5), Vol. 26. RTU. Riga. p. 21.–32.

Bubenko, J.A. jr, Persson, A., Stirna, J., 2001. User Guide

of the Knowledge Management Approach Using

Enterprise Knowledge Patterns. In: Deliverable D3,

IST Programme project Nr. IST-2000-28401. Dept. of

Computer and Systems Sciences, Royal Institute of

Technology, Stockholm, Sweden. Retrieved January

16, 2006, from

http://www.dsv.su.se/~js/ekd_user_guide.html

Cao, G., Clarke, S., Lehaney, B., 2003. Diversity

Management in Organizational Change: Towards a

Systemic Framework. In: Systems Research and

Behavioral Science, Vol. 20. John Wiley & Sons.

p.231.-242.

Daoudi, F., Nurcan, S., 2006. A Benchmarking

Framework for Methods to Design Flexible Business

Processes. In: Software Process Improvement and

Practice. John Wiley & Sons.

Grundspenkis J., 1983. The synthesis and analysis of

structure in computer aided design. In: Proceedings of

The 1st International Conference on Computer

Applications in Production and Engineering, North-

Holland Publ.Comp. p.301.-316.

Hatch, M.J., 1997. Organization Theory: Modern,

Symbolic, and Postmodern Perspectives, Oxford

University Press. New York.

ANALYSIS OF BUSINESS PROCESS FLEXIBILITY AT DIFFERENT LEVELS OF ABSTRACTION

395

Kalnins, A., Barzdins, J., Auzins, A., Etmane, I., Kalis, A.,

Podnieks, K., Tenteris, J., Vilums, E., Zarins, A.,

1996. Business Modeling Language GRAPES-BM

and Related CASE Tools. In: Proceedings of the

Second International Baltic Workshop "Databases and

Information Systems", Vol.2. Tallinn. p.3.-16.

Kirikova M., 2000. Explanatory capability of enterprise

models. In: Data &Knowledge Engineering 33.

p.119.-136.

Kumar, K., Narasipuram, M.M. Defining Requirements for

Business Process Flexibility. Retrieved January 16,

2006, from

http://lamswww.epfl.ch/conference/bpmds06/program/

Kumar_7.pdf

Osis, J., 1969. Topological Model of System Functioning.

In: Automatics and Computer Science, J. Latvian of

Acad. of Sciences, Nr. 6. Riga, Latvia. p. 44.-50. (in

Russian)

Osis, J., 2006. Formal Computation Independent Model

within the MDA Life Cycle. In: International

Transactions on Systems Science and Applications,

Vol. 1, Nr. 2. Xiaglow Institute, Glasgow, UK. p.159.–

166.

Regev,G., Wegmann, A. Business Process Flexibility:

Weick’s Organizational Theory to the Rescue.

Retrieved January 16, 2006, from

http://lamswww.epfl.ch/conference/bpmds06/program/

Regev_13.pdf

Regev, G., Soffer, P., Schmidt, R. Taxonomy of

Flexibility in Business Processes. Retrieved January

16, 2006, from

http://lamswww.epfl.ch/conference/bpmds06/taxbpfle

Skyttner, L., 1996. General Systems Theory An

Introduction, Antony Rowe. Chippenham, Wiltshire,

Great Britain.

Snowdon, R.A. (et al.), 2006. On the Architecture and

Form of Flexible Process Support. In: Software

Process Improvement and Practice. John Wiley &

Sons.

Sprice, R., Kirikova, M., 2005. Feasibility study: New

knowledge demands in turbulent business world. In:

Nilsson, G. (eds.): Information Systems Development -

Bridging the Gap between Academia and Industry,

Vol.1. Springer. p.131.-142.

ICEIS 2007 - International Conference on Enterprise Information Systems

396