
Semantic Relation Modeling and Representation for
Problem-Solving Ontology-based Linguistic Resources:
Issues and Proposals
Francisco Alvarez
1
, Antonio Vaquero
2
, Fernando Sáenz
2
and Manuel de Buenaga
3
1
Universidad Autónoma de Sinaloa, Ángel Flores y Vicente Riva Palacios
s/n, C.P. 80000, Culiacán, Sinaloa, México
2
Universidad Complutense de Madrid, Facultad de Informática
Departamento de Ingeniería del Software e Inteligencia Artificial
C/ Prof. José García Santesmases, s/n, E-28040, Madrid, Spain
3
Universidad Europea de Madrid, Departamento de Sistemas Informáticos
28670 Villaviciosa de Odón. Madrid, Spain
Abstract. Semantic relations are an important element in the construction of
ontologies and models of problem domains. Nevertheless, they remain under-
specified. This is a pervasive problem in Software Engineering and Artificial
Intelligence. Consequently, we find semantic links that can have multiple
interpretations in ontologies that support information systems, semantic data
models with abstractions that are not enough to capture the relation richness of
problem domains, and improperly structured taxonomies. However, if provided
with precise semantics, some of these problems can be avoided, and meaningful
operations can be performed on them. In this paper we present some insightful
issues about the modeling and representation of semantic relations that include
the available taxonomy structuring methodologies as well as the initiatives
aiming to provide relations with precise semantics. Furthermore, we explain
and propose the notion of control and verification of relations as a means to
properly structure ontologies.
1 Introduction
It has been suggested that ontologies can provide benefits for almost any knowledge
based information system. Among these suggested benefits is the ability to reuse an
ontology developed for one task in another task. However, there is one neglected
aspect that severely compromises the reusability and integration of ontologies:
semantic relations. Although they hold together the entities that represent a domain
and shape its structure, semantic relations have not been given the attention they
deserve. The focus has been on concepts, their properties and the operations that can
be performed on them, rather than on the semantics of relations.
Hence, in order to avoid some of the problems that arise from this neglectful
attitude, semantic relations (whether taxonomic or not) must be provided with fine-
grained semantics. This is an important issue, in particular for the development of
Alvarez F., Vaquero A., Sáenz F. and de Buenaga M. (2007).
Semantic Relation Modeling and Representation for Problem-Solving Ontology-based Linguistic Resources: Issues and Proposals.
In Proceedings of the 4th International Workshop on Natural Language Processing and Cognitive Science, pages 59-70
DOI: 10.5220/0002422700590070
Copyright
c
SciTePress

problem-solving ontology-based information systems. Tackling a precise task inside a
given domain requires precise semantics, not only at the concept level but also at the
relation level, that is, we should be able to describe relations in the same breadth of
detail as concepts.
As part of the SINAMED and ISIS projects [1], we have pointed out in [2, 3] the
need to: a) provide the relations used in ontologies with definite semantics and b) to
develop ontology-based linguistic resources (OBLR) following a software
engineering approach. Nonetheless, although a set of ideas has been proposed for the
representation of relations and their semantics, the results of our research stem mainly
from an analysis of “task-neutral” linguistic resources (LR) presented in [4].
In this paper, we present an analysis of the state-of-the-art in the representation of
semantic relations in Software Engineering (SE) and Artificial Intelligence (AI),
including the available methodologies to structure taxonomies. Our goal is to gain a
better insight of this normally neglected topic, underline its importance for the
development of information systems, and determine if the available technology is
well-suited to provide semantic relations with the level of granularity that problem-
solving ontology-based information systems need. Furthermore, we aim at covering
some of the blanks left in the current research regarding the representation of relations
and their semantics, and its possible application to the construction of domain and
task dependent ontologies and OBLR.
The rest of the paper is organized as follows. In section 2, the limitations of SE
techniques in the representation of relations are described. In section 3, the overstress
of concepts in detriment of relation representation in AI and taxonomy structuring
methodologies is shown. In section 4, the current initiatives to provide relations with
explicit semantics are presented. In Section 5, control and verification is introduced as
a meaningful operation based on the intrinsic semantics of relations. Finally, in
section 6, some conclusions and future work are outlined.
2 Semantic Relations in Software Engineering
Semantic relations (relationships in the SE vocabulary) are a key component of vital
design artefacts such as Entity-Relationship (E-R) models and object-class diagrams
(OCD). However, they only capture a limited set of relationships, leaving much of the
domain’s relationship structure out of the design [5].
In the E-R model [6] the model of the problem is represented by identifying its
entities, properties and relationships. In this model, relationships are classified among
entities as binary, n-ary, or recursive. Nonetheless, although they are depicted on the
E-R diagram, the amount of information they convey is rather limited, that is, the
model itself only provides minimal information describing the relationships (i.e.
mainly the cardinality among entities).
In OCD [7, 8], objects are organized by their similarities into classes that describe
a set of objects having the same attributes and behavior patterns. In these models,
relationships among classes can be classified under three basic categories denoting: a)
generalization-specialization; b) whole-part/aggregation and c) an association among
otherwise unrelated classes.
60

In OCD, generalization and aggregation types of relationships are strongly defined
among classes. Nevertheless, all other types of relationships that exist in the problem
domain are lumped into the association category and depicted by a name connecting
the classes. These names only indicate that a dependency exists but do not explicitly
indicate how. Thus, association relationships are identified more implicitly than
explicitly. Furthermore, the distinction between aggregation and association is often a
matter of state rather than a difference on semantics [9].
In the UML [10] relationships suffer from the same under-specification. The UML
categorizes relationships under five categories: association, aggregation (denoting a
part-of relationship), dependency, generalization-specialization (denoting an is-a
relationship) and realization. As with OCD relationship classification, generalization
and aggregation relationships are strongly defined among classes. However,
association, dependency and realize relationships have to be identified by looking at
the sequence and collaboration diagrams. Furthermore, only a label is used to indicate
that these relationships exist. Thus, as in OCD, they are identified more implicitly
than explicitly.
Although we have described just a few semantic data models here, several others
suffer from the same problem: namely minimal information describing relationships.
As can be seen, relations are neglected in favor of object or entity representation.
However, as it will be shown next, this is not inherent to SE; it is also a pervasive
phenomenon in AI.
3 Semantic Relations in Artificial Intelligence
In AI, we find that knowledge representation formalisms (e.g. DAML and OWL) are
intended to describe the terminology of a domain in terms of classes/concepts
describing sets of individuals and properties/roles relating these [11]. However,
although in the above formalisms is possible to make statements about a set of
concepts, such as to declaratively specify that two classes are disjoint; analogous
declarative statements are not possible for relations. This also comprises the
assignment of properties, while concepts are assigned with as many properties as
needed, the same level of precision cannot be applied to semantic relations.
Furthermore, the modeling effort is done through the construction of subsumption
hierarchies among the defined classes and properties, that is, taxonomic reasoning is
restricted to a generalization-based one. This is partially caused by the lack of
conclusive mechanisms to reason along other types of relations [12], and because,
generalization was initially regarded as the primary mechanism for mastering the
complexity of domains.
Consequently, there is a subsumption overload that has led to the misuse,
confusion and conflation of semantic relations due to the lack of analysis to: a)
distinguish between the different relations to be used in the representation of a domain
and b) precise the semantics of these relations. For instance, without such an analysis
what we have are ontological resources that have very general or under-specified
relations that cannot be adequately interpreted [13], resources whose relations are
subject to multiple interpretations [11], resources where the semantics of the relations
are not fine-grained enough as to allow to differentiate between two relations that are
61

close in meaning but are not the same (e.g. the is-a and hypernym relations [14]), and
improperly structured taxonomies.
For instance, in SNOMED-RT (a clinical terminology developed by the College of
American Pathologists), the concept “testis” subsumes (correctly) the concepts “left
testis”, “right testis” and “undescended testis”, but also “both testes”. We could accept
“both testes” as being part-of another concept (e.g. “Testes”) denoting the
mereological sum of the left and right testes, but hardly as being a “Testis”. In this
case, the mistake is introduced manually by one of the ontology developers who
incorrectly assigned a direct is-a link. Figure 1 shows this mistake.
Fig. 1. Wrong Modeling Choice.
Similarly and again in SNOMED-RT, “Hair” subsumes (correctly) “Vellus Hair”
and “Terminal Hair”, but also “Hair Shaft”. However, a quick look in a dictionary
will tell us that “Hair Shaft” is not a kind of “Hair” but part-of it.
This kind of problems has received most of the attention in AI. However, as it will
be seen, the available approaches for taxonomy structuring focus more on concepts
and their properties rather than on relations and their semantics. Moreover, although
the ontology structuring problems represent a serious obstacle in the development and
integration of ontological resources, there are only two proposals that actually deal
with it: The OntoClean [15] and [16] methodologies. These methodologies are similar
but at the same time, as it will be seen below, follow opposite approaches to attain the
same goal.
3.1 The Metaphysical Approach of OntoClean
OntoClean is grounded on the philosophical and metaphysical ideas of essentialism
[17] that state that for any specific kind of entity (e.g. a tiger), it is theoretically
possible to specify a finite list of properties (e.g. the rigidity, identity and unity
metaproperties of OntoClean) all of which any entity must have to belong to a
specific group or natural kind (e.g. see the table of properties and the taxonomy of
kinds in [15].
It is also influenced by the ideas of psychological essentialism [18] that enunciate
that the world is divided into essences from which preset associated properties can be
inferred (e.g. the metaproperties mentioned above), and that these properties play a
key role in our everyday reasoning and categorization tasks by backing-up our
inferences about kind membership.
Hence, OntoClean can be understood as a reasoning heuristic and inference system
that establishes that the compatibility between the metaproperties defining the essence
of concepts determine if a concept can subsume another and vice versa.
62
Nevertheless, a global theory of reference and categorization, independent of any
domain and task, like the one OntoClean provides is not possible. Recent work in
cultural psychology has shown systematic cognitive differences between East Asians
and Westerners, and some work indicates that this extends to intuitions about
philosophical cases [19].
Furthermore, it is interesting to note that just like in OCD and the UML, the
generalization (is-a) and aggregation (part-of) relations are strongly defined in
OntoClean. This is done through an axiomatization (see the set of definitions in [15])
that presents itself as an absolute truth. However, just like OCD, any other relation
that falls out of the scope of the methodology cannot be described nor controlled.
Hence, the limited set of abstractions wherewith OntoClean pretends to master the
complexity of any domain and structure an ontology is not enough. Figure 2 shows
the OntoClean approach.
Fig. 2. The OntoClean Approach.
3.2 The Linguistic Approach of Archonte
Archonte relies on the work of [20] that states that even for well-defined domains, the
norms that fix the meaning of a word and of its reference (e.g. its concept) cannot be
foreseen, and that the meaning of words is immanent to a given situation and context
of usage. Archonte claims to provide concepts with a domain and task-dependent
meaning by means of the similarities and differences that a linguistic unit has with
other neighboring units in the same context of usage, and that this differences and
similarities can be found by analyzing a corpus
This method requires the use of terminological extraction tools to discover
candidate concepts from the corpus. Once this is done, it uses a set of principles [16]
to create and structure a backbone taxonomy where the differences and similarities
between concepts are expressed in natural language. This is much in the spirit of the
taxonomies found in machine-readable dictionaries. Nonetheless, while these
taxonomies are twisted, Archonte provides a manual method to create properly
structured linguistic taxonomies from words with the aid of an expert.
The principles are the following: a) similarity with parent (SWP); b) similarity with
siblings (SWS); c) difference with siblings (DWS) and d) difference with parent
(DWP). Since these principles are attached to concepts, herein lies the similarity with
OntoClean. In order to structure an ontology, concepts (not relations) must have a set
63

of (meta) properties that determine if a semantic link can exist between any two
concepts. Nonetheless, although Archonte claims to be domain and task-dependent, it
is clear that it is only domain-dependent. Concepts and relations are obtained by
processing a domain-dependent corpus, but the corpus itself is independent of any
task, as well as the set of properties used to arrange the concepts. Figure 3 illustrates
the Archonte approach.
Fig. 3. The Archonte Approach.
Given the evidence, we claim that structuring an ontology cannot be done relying
on the properties of concepts. The aforementioned task must be done by putting the
entire semantic load on the relations. In the next section, we will try to clarify this last
point.
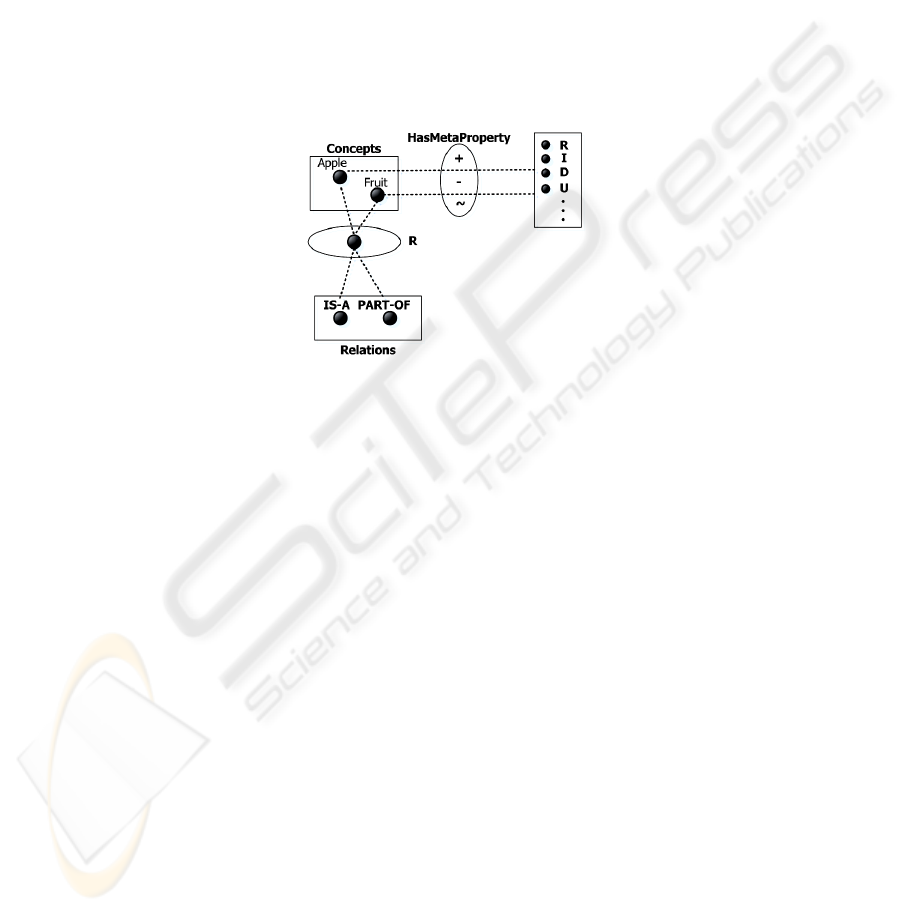
4 Refining and Describing Semantic Relations
In [4] we do an analysis of “task-neutral” LR and point out the need to provide
relations with intrinsic semantics in order to prevent the taxonomic flaws of these
resources, and in [2, 3] we propose to divide the semantics of relations into algebraic
and intrinsic properties and to apply the principles of SE to the development of
OBLR. Nonetheless, several things were left out.
First, do SE and AI provide the tools to supply semantic relations with the level of
granularity that is needed for the development of software engineered, domain and
task-dependent OBLR? Second, do taxonomy structuring methodologies actually deal
with the contents of the semantic link around which the backbone taxonomy is
constructed? Third, although the algebraic properties of relations can be well
understood in our proposal [2], the intrinsic properties are left unspecified. Hence,
what could these intrinsic properties be? What is the meaning they could convey?
What would they be useful for?
Sections 2 and 3 provide an answer for the first two questions. As for the third one,
relation element theory (RET) provides an answer. As explained in [21], RET is an
effort to provide an exhaustive as possible classification (under the form of a
taxonomy) of binary semantic relations (here, the reader must notice the resemblance
between RET and the relationship classification of OCD), on the basis of the nature of
the relation between a parent or domain concept and a child or range concept.
However, although it would be very difficult to derive an exhaustive and universally
agreed upon taxonomy of relations, a set of relation elements or relation primitives
64

are proposed that could be used to describe and refine the semantics of a relation
between two entities. These elements are the following: Composable, Connected,
Functional, Homeomerous, Intangible, Intrinsic, Near, Separable, Structural and
Temporal.
A possible application of these primitives would allow countering the polysemy
and synonymy of relations within a same knowledge domain or context. For instance,
a relation part-of relating an entity Engine to another entity Car could be defined
synonymously in another ontology as “physicalParts”, but a machine without prior
definitions cannot infer that these two relations are identical. Moreover, providing that
we have a suitable algebra, there is the possibility of doing plausible inference [21] by
using the semantic primitives of relations to infer new relation instances between sets
of entities.
However, although the use of the aforementioned set of primitives can clarify the
underlying semantics of relations, and meaningful operations can be performed with
them, it seems that these primitives conflate several properties that should be
separately and explicitly represented as part of the semantics of a single relation or
they simply ignore these properties despite the fact that, as it will be seen below, these
properties stem from the definition of the primitive itself.
4.1 Algebraic and Intrinsic Properties of Relations
First, the primitive Connected indicates that the domain element is temporally or
physically connected to the range element either directly or transitively. Here,
direction and transitivity are conflated into one single primitive and made inherent to
the primitive itself. This is a mistake, because for a given domain, a relation can be
directed and transitive or directed and non-transitive, as demonstrated by [22] in their
analysis of semantic relations in the medical domain.
For instance, Perforation-of-Appendix implies a perforation of the Intestine
because Appendix is part-of Intestine, but Appendicitis (Inflammation of the
Appendix) does not imply an inflammation of the Intestine. Similarly, Glomerulus is
part-of Kidney, and Appendix is part-of Intestine. However, although
Glomerulonephritis (an inflammation of the Glomerulus) is-a Nephritis (an
inflammation of the kidney), an Appendicitis is not an Enteritis (inflammation of the
Intestine).
Second, the primitive Intangible denotes that the relation that links the domain and
range elements is hierarchical with regard to ownership or mental inclusion. However,
it is well-known that hierarchical relations (e.g. is-a and part-of), can have a set of
algebraic properties (e.g. asymmetry, irreflexivity, transitivity, etc.) that are useful to
make valid syllogistic inferences. Nonetheless, it is unknown (as it is not explicitly
stated) if the primitive comprises any of these properties or others.
Third, the Structural primitive specifies that the domain and range elements have a
hierarchical relationship in which the domain element is below the range element in
the hierarchy. Basically, what this primitive is telling us is that the range subsumes
the domain or vice versa. Nevertheless, as with the Intangible primitive the set of
algebraic properties related to hierarchical relations are simply ignored.
In spite of this, [21] argues that the scope of these primitives could be restricted to
a knowledge domain of interest or to a context within a knowledge domain, in order
65

to avoid the complications that arise when aiming for a universal set of primitives that
could describe every relation in every domain. RET, just like OCD, UML, OntoClean
and Archonte, seeks universality by using a small set of abstractions to model a
domain.
In [2], we propose to represent semantic relations in terms of intrinsic and
algebraic properties. We achieve several objectives by partitioning the semantics of
relations this way: a) to separate those properties needed to make syllogistic
inferences (e.g. transitivity) from any domain or task dependent properties (as it will
be seen below); b) to avoid making any property or primitive a general definitional
property of a relation; c) to allow making fine-grained distinctions for each relation
independently of any knowledge representation language.
Nevertheless, it has to be clearly stated that, as opposed to RET, we do not aim for
an exhaustive classification of relations nor do we propose a universal set of
properties through which any relation can be represented. We just propose to
represent relations with well-defined semantics up to the granularity that is needed for
the task at hand.
Therefore, for a given domain and task, each relation must be provided with a set
of properties defining its semantics. Thus, we have algebraic properties that are
domain-independent and intrinsic properties that are domain-dependent and task-
dependent. This is necessary for modeling non-formal domains like medicine where
we not only need to define relations with a simple tag, but also to qualify or precise
the relations that link a part and a whole, a child and a parent, etc. with additional
attributes. Some examples taken from the medical domain might help to clarify our
point.
4.1.1 Modeling Relations in the Medical Domain
In the medical domain, the part-of relation not only states that A is part of B, it also
needs a set of properties to precise its meaning within a given context. For example,
parts of an organ can be shared (they belong to several anatomical entities) or
unshared (they belong to a single anatomical entity). Blood vessels and nerves that
branch within a muscle must be considered a part-of that muscle and of the vascular
or neural trees to which they belong. In contrast, the fleshy part-of the muscle (made
of muscle tissue) and the tendon (made of connective tissue) are unshared.
Similarly, the “adjacent to” relation not only expresses that A is adjacent to B, it
also must have a set of attributes defining the adjacency: left, right, inferior, posterior,
etc. In figure 4, we can see an example of this. The brachialis is “adjacent to” the
bicep tendon but is located behind (posterior to) it. The same applies to any other
relation that is necessary to model a domain.
Furthermore, we must “artificially” subdivide a domain according to the demands
of a given task. Hence, if for a given anatomical structure, we want to record the site
of an injury with precision we must further subdivide it in terms of concepts and
relations, in order to capture the granularity of this task.
For instance, as can be seen in figure 4, the biceps muscle has several anatomical
parts that are structurally distinct from one another (i.e. a long head, a short head, a
belly, a tendon). Nonetheless, if we want to record the site of an injury with precision
in this structure, we must distinguish the intracapsular part of the tendon of the long
66
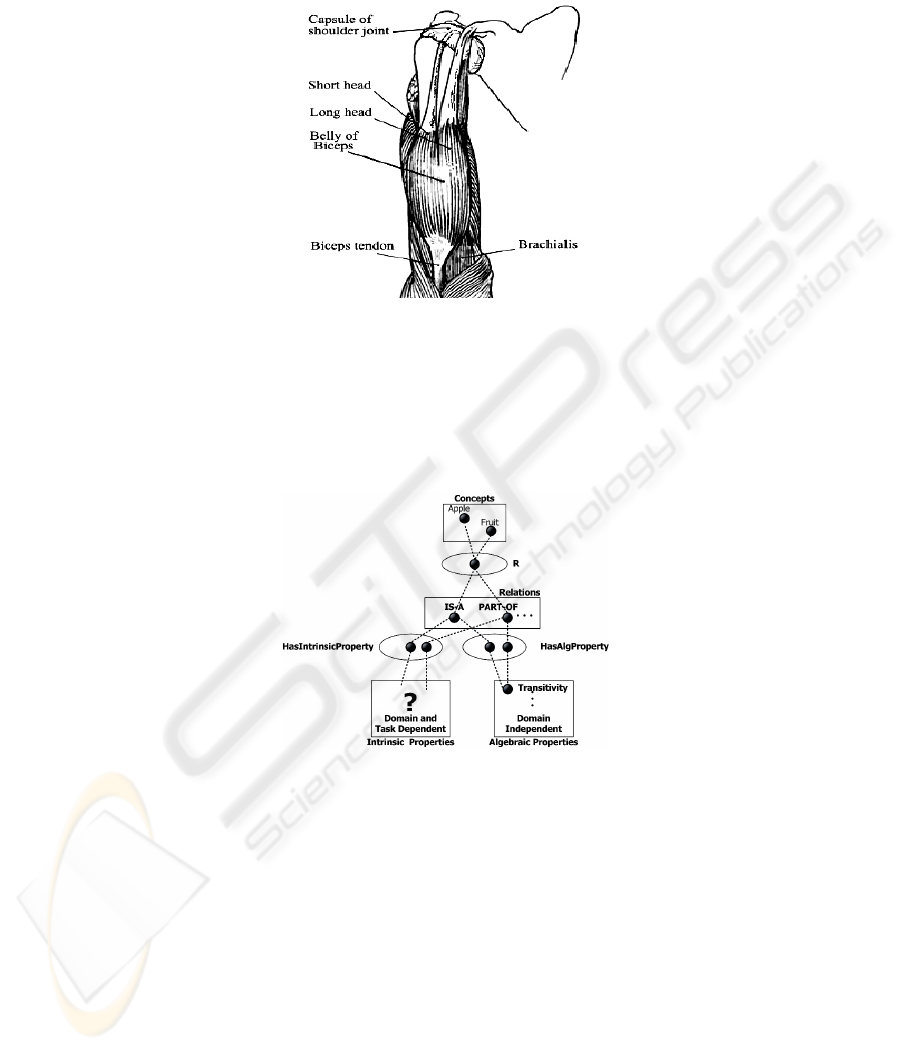
head of the biceps (which is enclosed within the capsule of the shoulder joint) from
the extracapsular part of the same tendon.
Fig. 4. The Biceps and its Parts.
This is precisely what OntoClean, Archonte, RET and even description logics
cannot provide: the fine-grained distinctions that a problem-solving task in a given
domain requires in terms of relation representation, because the nature and number of
relations covering any domain and task is impossible to foresee. Figure 5 shows the
proposed approach for relation representation.
Fig. 5. Algebraic and Intrinsic Properties of Relations.
Based on these ideas we introduce the notion of control and verification of
semantic relations, a notion that we will try to clarify in the following section.
5 Control and Verification of Semantic Relations
Of the many difficulties in building a useful knowledge-based system (KBS),
verification is one of the greatest challenges, and as we automate even more and more
tasks the need for verification becomes even more crucial [23].
67

As far as semantic relations are concerned, control and verification entails that for
a given domain and task, a set of conditions must be established to test whether two
concepts can be linked by a given relation. Nevertheless, this can only be enforced but
through the use of relations with well-defined semantics highly dependent on the
domain and task.
The goal is to properly structure an ontology by using a set of properties that can
act as domain constraints, without resorting to the metaphysical universality or to the
text-dependent generality of the available taxonomy structuring methods, as they do
not take into account the semantics of relations nor the task for which an ontology is
being built. Consequently, a complete set of relations must be identified and
documented early at the development process by doing an analysis of the domain and
the task to be carried out. Moreover, for each relation, its set of intrinsic and algebraic
properties must be established as well.
Let us suppose that we are trying to develop an ontology to support a legal
information system to “assess claims for immigration” in “Schengen signatory
countries”. Our domain analysis might show that only the is-a relation is needed to
model the problem domain with the following properties: a) asymmetry, reflexivity
and transitivity as algebraic properties; b) has borders, has constitution and has central
government as domain-dependent intrinsic properties; and c) signed treaty of
adhesion and signed Schengen agreement as task-dependent intrinsic properties.
Based on these properties, the system could ask meaningful questions to the ontology
developer in order to prevent inappropriate modeling choices. Figure 6 illustrates
this.
Fig. 6. A Domain Modeled with a Single Relation.
Fig. 7. A Plausible Modeling Choice.
With this approach, wrong modeling choices like the one in figure 1 can be
avoided and plausible representations like the one in figure 7 (for the testis example in
68

section 3) can be obtained. Nevertheless, the concepts and relations shown in this
figure, as discussed in the previous section, would represent facts about the domain,
and some would be needed to support a given task.
6 Conclusions and Future Work
Semantic relations are an important part in the construction of the model of a problem
domain in SE and AI. However, they have been neglected in favor of concepts or
entities.
In SE, semantic data models have an emphasis on entity representation.
Relationship representation is done through a. small set of fundamental abstractions
and when a relationship falls outside their scope it is loosely defined and represented
by a tag, or lumped under a category that does not account for its semantics.
In AI, the level of semantic precision in terms of properties and attributes, as well
as the operations that can be performed on semantic relations is surprisingly low. AI
does not provide any tools for the description and refinement of semantic links up to
the granularity needed for the task or problem at hand. Moreover, although the under-
specification of semantic links has been pointed out for main OBLR [4, 11], few
initiatives [2, 21] exist that aim at providing not only a richer semantics to these links
but also to propose specific operations that can be performed on them.
From the operations that can be performed on semantic relations, we are interested
in control and verification, as we believe it would allow the kind verification (at least
for semantic relations in ontologies in general) that [23] argues that KBS need.
Furthermore, their enforcement through the properties of relations would allow to
properly structure an ontology. We claim that this structuring is dependent not only
on the domain but also on the task for which the resource is being built; as it is the
context of the task (a specific application) the one that allows fixing the pertinent
meaning features of concepts and relations.
Finally, we propose the inclusion of control and verification of semantic relations
as part of a methodological framework for the development of OBLR with relational
databases. By doing this we go, qualitatively, further than any other efforts [24] that
have used relational databases to build a LR with a Mikrokosmos-like philosophy and
structure [25] for specific applications. We are currently in the stage of: a) building a
text corpus for the domain of Pneumonia; and b) developing a tool based on the one
described in [24] in order to include the ideas mentioned here. Our final goal is to
develop an OBLR that will be used as part of a summarization and categorization
system.
References
1. Buenaga, M. et al. The SINAMED and ISIS Projects: Applying Text Mining Techniques to
Improve Access to a Medical Digital Library. LNCS 4172, pp. 548-551, 2006.
2. Vaquero, A. et al. Conceptual Design for Domain and Task Specific Ontology-Based
Linguistic Resources. LNCS 4275, pp. 658-668. 2006.
69

3. Vaquero, A. et al. Thinking Precedes Action: Using Software Engineering for the
Development of a Terminology Database to Improve Access to Biomedical Docu-
mentation. LNCS 4345, pp. 207-218. 2006.
4. Vaquero, A. Álvarez, F. and Sáenz, F. A Review of Common Problems in Linguistic
Resources and a New Way to Represent Ontological Relationships. Electronic Journal of
the Argentine Society for Informatics and Operations Research, Vol. 7(1), ISSN 1514 -
6774, pp. 1-11. 2007.
5. Yoo, J., Catanio, J. and Ravi, P. Relationship Analysis in Requirements Engineering.
Requirements Engineering, Vol. 9(4), pp. 238-247. 2004.
6. Chen, P. The Entity-Relationship Model – Toward a Unified View of Data. ACM
Transactions on Database Systems 1(1). 1976.
7. Booch, G. Object-Oriented Development. IEEE Transactions on Software Engineering
12(12). 1986.
8. Rumbaugh, J. 1991. Object-Oriented Modeling and Design. Prentice-Hall, New Jersey.
9. Steimann, F., Gößner, J. and Mück, T. On the Key Role of Composition in Object-Oriented
Model-ing. LNCS 2863, pp. 106–120, 2003.
10. Booch, G., Rumbaugh, J & Jacobson, I. The Unified Modeling Language User Guide.
Addison Wesley. 1999.
11. Kashyap, V. and Borgida, A. Representing the UMLS® Semantic Network using OWL.
LNCS 2870, pp. 1-16. 2003.
12. Schulz et al. From Knowledge Import to Knowl-edge Finishing: Automatic Acquisition and
Semiau-tomatic Refinement of Medical Knowledge. In Proc. of the 12th Banff Knowledge
Acquisition for Knowl-edge-Based Systems Workshop - KAW'99. 1999.
13. Nirenburg, S. et al. Ontological Semantic Text Processing in the Biomedical Domain.
Working Pa-per #03-05, Institute for Language and Information Technologies, University
of Maryland. 2005.
14. Hirst G. Ontology and the Lexicon. In Staab & Studer (eds), Handbook on Ontologies,
Springer-Verlag, pp. 209-230. 2004.
15. Welty, C. & Guarino, N. Supporting Ontological Analysis of Taxonomic Relationships.
Data and Knowledge Engineering, Vol. 39(1) Elsevier. 2001.
16. Bachimont, B., Isaac, A., Troncy, R. Semantic Commitment for Designing Ontologies: A
Proposal. LNCS 2473, pp. 114-119. 2002.
17. Barrett, H.C. On the Functional Origins of Essentialism. Mind and Society 3(2), pp. 1-30.
2001.
18. Medin, D. & Ortony, A. Psychological Essentialism. In S. Vosniadou & A. Ortony (eds.)
Similarity and Analogical Reasoning. Cambridge University Press, pp. 179-195. 1989.
19. Machery, E. et al. Semantics Cross-Cultural Style. Cognition 92, pp.B1-B12. 2004.
20. Rastier, F., Cavazza, M., Abeillé, A. Sémantique pour l'analyse. De la linguistique à
l'informatique, Masson. 1994.
21. Russomanno, D. A Plausible Inference Prototype for the Semantic Web. Journal of
Intelligent Informa-tion Systems, Vol. 26(3), pp.227-246. 2006.
22. Hahn, U., Schulz, S., Romacker, M. 1999. Part-whole Reasoning: A Case Study in Medical
Ontology Engi-neering. Intelligent Systems and their applications, Vol. 14(5), pp.59-67,
IEEE Computer Society.
23. Hicks, R.C. 2003. Knowledge-Based Management Sys-tem-Tools for Creating Verified
Intelligent Systems. Knowledge Based Systems 16, pp. 165-171.
24. Moreno, A. and Pérez, C. 2000. Reusing the Mikrokos-mos Ontology for Concept-Based
Multilingual Ter-minology Databases. In Proc. of the 2nd LREC, pp. 1061-1067.
25. Viegas, E. et al. 1999. Semantics in Action. In P. Saint-Dizier (ed.), Predicative Forms in
Natural Language and in Lexical Knowledge Bases, Kluwer, pp. 1-33.
70
