
Recognition of Multiple Objects with Adaptive
Correlation Filters
Marco I. Pinedo-García
1
, Victor H. Diaz-Ramirez
2
and Vitaly Kober
2
1
Electronics and Telecomunication Department, CICESE, Km. 107 carretera
Tijuana-Ensenada B.C., CP22860, Mexico
2
Computer Science Department, CICESE, Km. 107 carretera
Tijuana-Ensenada B. C. CP22860, Mexico
Abstract. A new method for reliable optical pattern recognition of multiple ob-
jects in a cluttered background and consequent classification of the detected ob-
jects is proposed. The method is based on an adaptive composite correlation fil-
ter. The filter is designed with the help of an iterative algorithm exploiting a
modified version of synthetic discriminant function filter. The impulse response
of the filter contains information needed to localize and classify objects belong-
ing different classes. Computer simulation results obtained with the proposed
method are compared with those of known correlation based techniques in
terms of performance criteria for recognition and classification of objects.
1 Introduction
A number of techniques and algorithms based on different criteria have been pro-
posed to solve effectively one of the two different recognition tasks: detection of
targets and classification of given objects. However, in real applications often these
two problems cannot be separately considered. For instance, several objects and their
geometrically distorted versions are embedded into a cluttered noisy background.
Basically, heuristic digital systems based neural networks and evolutionary algo-
rithms use two-step processing: segmentation and classification. Such the systems are
not able correctly to detect and perform segmentation of distorted objects, which are
embedded in cluttered noisy scenes. Correlation-based methods possess a good
mathematical basis to detect and localize (estimation of the target position) objects.
Many correlation filters optimized with respect to different detection criteria have
been proposed [1]. Note that detection and classification of multiple objects are com-
putation-intensive processing tasks. Correlation filters can be implemented optically
or by the use of hybrid (optodigital) systems at a high rate [2]. Optical correlators are
inherently shift invariant, producing correlation peaks that indicate both presence and
location of input objects. In order to detect and classify objects with the use of corre-
lation operation the following methods are proposed: (i) time-sequenced filtering [3],
in which multiple filters (one for each version of the input object) are sequenced
rapidly in and out of the filter plane, yielding a sequence of output correlation re-
I. Pinedo-García M., H. Diaz-Ramirez V. and Kober V. (2007).
Recognition of Multiple Objects with Adaptive Correlation Filters.
In Proceedings of the 7th International Workshop on Pattern Recognition in Information Systems, pages 199-206
DOI: 10.5220/0002423201990206
Copyright
c
SciTePress

sponses; (ii) space multiplexed [4] or spatial frequency multiplexed [5] filtering, in
which all filters are presented simultaneously in the filter plane, yielding an array of
multiple correlation responses; (iii) combination filtering, in which several filters are
combined to form a composite filter that yields a detectable output correlation re-
sponse for any set of input objects [6]. The last method may be utilized to construct a
bank of composite filters that can be used as time-sequenced or multiplexed filters.
Note that time-sequenced and space-multiplexed filtering requires a large number of
correlations, because a single filter for each object and each its distorted version is
used. To reduce the number of filters Braunecker et al. [7] proposed to carry out only
(
)
2
log N correlations by forming primitive composite filters from similar patterns,
where N is the number of patterns to be recognized,. A drawback of this method is
that it works only with binary images. Billert and Singher [8] suggested to reduce the
number of correlations by employing different composite filters, each of them is able
to recognize a set of training images. The filters possess a good tolerance to additive
noise at the input scene. Nevertheless, the filters work well only with binary-
segmented images.
One of the most important performance criteria in pattern recognition is the dis-
crimination capability (DC), or how well a filter detects and discriminates different
classes of objects. Yaroslavsky [9] suggested a correlation filter with a minimum
probability of anomalous errors (false alarms) and called it the optimal filter (OF).
The disadvantage of the OF in optical implementation is its extremely low light effi-
ciency. A filter with maximum light efficiency is the phase-only filter (POF) [10].
The POF produces sharp correlation peaks but possesses a poor performance in terms
of the DC for noisy and cluttered scenes. An attractive approach to distortion-
invariant pattern recognition is based on synthetic discriminant functions (SDF) filters
[11]. A conventional SDF filter is composed by a linear combination of training im-
ages. It is able to control only one point at the correlation plane for each training
image. As a result, the SDF filters often have a low discrimination capability. Maha-
lanobis, et al, [12] suggested the minimum average correlation energy (MACE) filter.
The MACE filter produces sharp correlation peaks by minimizing the average of
correlation energy in the correlation plane. However, the MACE filter is not tolerant
to input noise, and it is more sensitive to interclass variations than other composite
filters. The main efforts in correlation filter research are focused to the problem of
recognition and localization of objects, and commonly ignoring the problem of classi-
fication. This paper is devoted to the design of new correlation filters for solving the
following two problems: reliable recognition and correct classification of all desired
objects, which are embedded into a cluttered noisy background. These problems may
be solved with the help of adaptive correlation filters [13], [14]. In order to obtain the
impulse response of an adaptive filter an iterative algorithm is used. At each iteration,
the algorithm suppresses the highest sidelobe at the correlation plane. Therefore, it
increases monotonically the DC until a prespecified value is reached. The object
classification is carried out using the phase information at the origin of the correlation
peak for each target. The proposed method requires only one correlation to detect and
classify all needed objects. This paper is organized as follows. Section 2 presents a
basic description of pattern recognition based on conventional SDF filters, as well as
a modified SDF approach proposed for object classification. The proposed algorithm
200

of the adaptive filter design is given in Section 3. Computer simulation results ob-
tained with the proposed filter are presented and discussed in Section 4. Finally, Sec-
tion 5 summarizes our conclusions.
2 Pattern Recognition and Classification with SDF Filters
Assume that we have a set of objects (including distorted versions) to be recognized.
For simplicity, we consider a two-class recognition problem. Let us define the true
class as different versions of an object to be recognized. The false class consists of all
non-desired objects to be rejected including a cluttered background. The impulse
response of a SDF filter is as a linear combination of training images. Let {s
i
(x, y) |i =
1, . . . , N} be a set of linearly independent training images each with M pixels. The
SDF filter in a matrix-vector notation can be expressed as follows:
h = S a,
(1)
where S is a matrix with N columns and M rows, and its ith-column is given by the
vector version of s
i
(x,y), a represents a column vector of the weighting coefficients
{a
i
|i = 1, . . . ,N}. The vector a must be determined in order to satisfy the following
constraints:
c = S
+
h.
(2)
Here, the superscript ”+” means conjugate transpose. Substituting Eq. (1) into Eq. (2),
and if the matrix R = (S
+
S) is non-singular, the vector solution of the equation system
is given by
a = (S
+
S)
-1
c,
(3)
and finally, the filter vector is
(
)
1−
=
+
hSSS c.
(4)
To recognize distorted versions of the desired class and to reject all objects of the
false-class, we set up the elements of c corresponding to the desired and non-desired
objects to unity and zero, respectively,
c = [1, 1, …, 1, 0, 0, …, 0]
T
.
(5)
This approach can be easily extended to any number of classes.
2.1 Pattern Classification with a Modified SDF Filter
In order to design a SDF filter for multiclass pattern recognition, we can set up for
each class different real values in the vector c. These values must be within the range
of [0, 1]. However, the use of values less than unity in the vector c for different true-
classes affects severely the discrimination capability. In other words, the correlation
peaks of objects belonging to a true-class will be lower than the maximum value. This
201

means that false alarms become very likely. We propose to set the filter output as
complex values in a unitary circle as follows:
c = {exp(i β
j
) | j = 1,…, K; β
j
Є R},
(6)
where K is the number of true-classes. In this way, we can obtain the maximum inten-
sity correlation peak for each target-object. Note that information about the classes is
contained in the phase distribution of the complex correlation plane at the coordinates
of the maximum intensities. Using such a filter for multiclass pattern recognition, we
expect that the correlation peak intensities of targets will be close to unity for all true-
classes, whereas the cross-correlation peak intensities of non-desired objects will be
close to zero, i.e.,
c = [exp(i β
1
), …, exp(i β
K
), 0,…, 0]
T
. (7)
3 Design of Adaptive Correlation Filters for Pattern Recognition
and Classification
Commonly, correlation filters are designed to be optimum with respect different per-
formance criteria. The discrimination capability is one of the most important metrics.
It is defined as the ability to a filter to distinguish a target among other different ob-
jects. The DC can be expressed as follows:
()
()
2
2
0, 0
1
0, 0
B
T
C
DC
C
=−
,
(8)
where |C
B
|
2
is the maximum intensity in the correlation plane over the area of a back-
ground to be rejected, and |C
T
|
2
is the maximum intensity in the correlation plane over
the target position. The area of target position is determined in the close vicinity of
the actual target location. The area of background is complementary to the area of the
target position. The impulse response of an adaptive correlation filter can be obtained
with the help of an iterative algorithm shown in Fig. 1. The proposed algorithm is
given as follows.
1. Assign all targets (including distorted versions) belonging to various true-classes
to different regions in a unitary circle according to Eq. (6).
2. Create a SDF filter trained only with targets (including distorted versions) using
Eqs. (4) and (7).
3. Carry out independently correlations between the adaptive SDF filter and all ob-
jects including the background.
4. Calculate DC using Eq. (8).
5. If DC is greater or equal to the desired value, the procedure is finished, else go to
the next step.
202
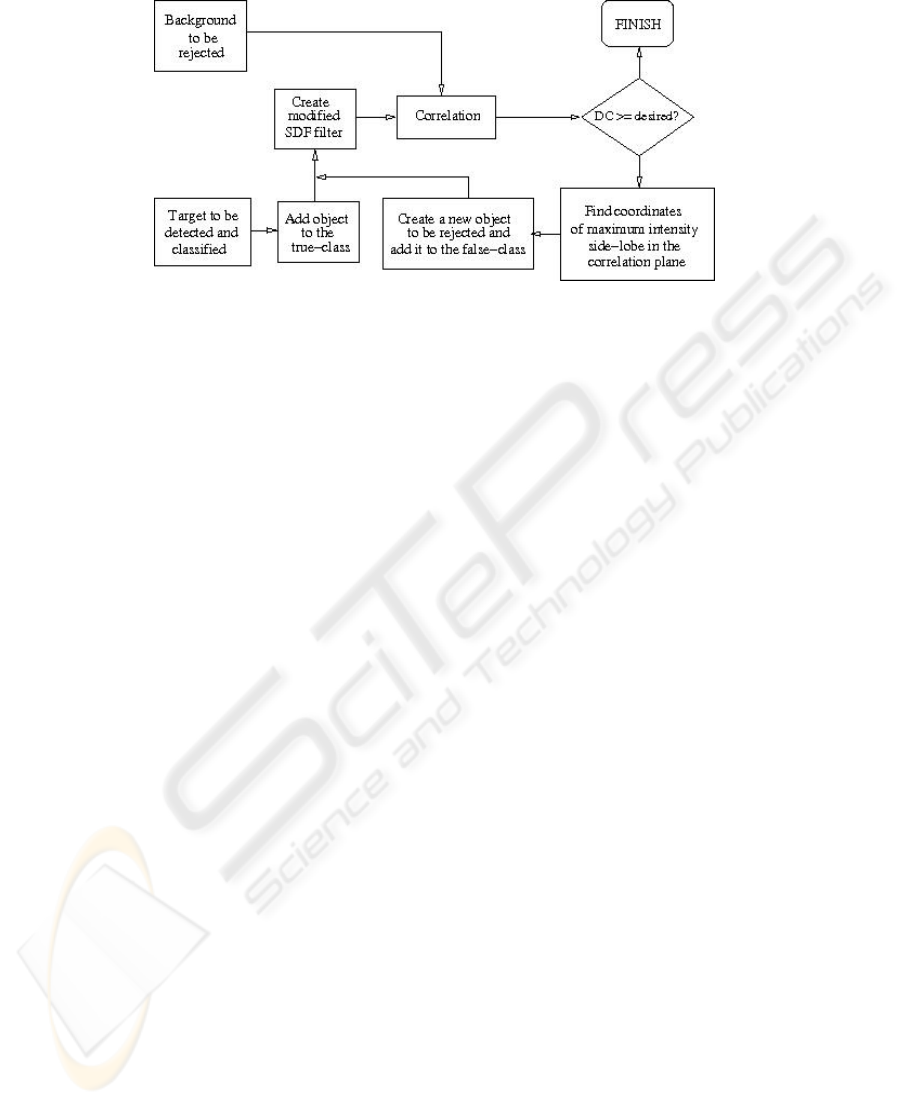
Fig. 1. Block-diagram of the iterative algorithm for the filter design.
6. Create a new object to be rejected. The origin of the object is taken at the coordi-
nates of maximum intensity in the correlation plane. The region of support of the
new object is the union of shapes of all targets. This new object is included into the
false-class.
7. Create a new adaptive SDF filter utilizing the multiclass recognition problem. The
true-classes contain all targets and the false-class consists of objects to be rejected.
Go to step 2.
4 Computer Simulations
In this section, results obtained with the adaptive SDF filter are presented. Fig. 2
shows an input scene containing three different fish-targets (t1, t2, t3). Four geomet-
rically distorted versions for each target were used. We utilized two versions rotated
with -5 and 5 degrees, and two versions scaled by factors of 0.9 and 1.1. All images
used in simulations are monochrome with a signal range of [0, 255]. The size of the
images is 256x256 pixels. The targets are located at unknown coordinates in an in-
homogeneous background. The goal of our simulation is to design an adaptive SDF
filter that is able to recognize the target (and its geometrically distorted versions) and
correctly classifies them.
We compare the performance of the proposed filter in terms discrimination capability
and classification efficiency with a modified time-sequenced method [3] employing
banks of the following filters: the matched spatial filter (MSF) [15], the POF, the OF,
and the SDF. The postprocessing algorithm for classification of all objects can be
illustrated with three objects as follows: (i) design a correlation filter F1 to detect t1
and to reject t2 and t3; (ii) design a filter F2 to detect t2 and to reject t1 and t3; (iii)
design a filter to detect t3 and to reject t1 and t2; (iv) carry out the correlation be-
tween the input scene and F1, F2, and F3 obtaining the correlation planes C1, C2, and
C3, respectively; (v) localize the maximum intensity values in each correlation plane
203

(a) (b)
Fig. 2. (a) Test input scene, and (b) three targets.
obtaining
1C
M
AX ,
2C
M
AX , and
3C
M
AX ; (vi) if
213CCC
M
AX MAX MAX
<
> , then
the input object is t1, if
123CC C
M
AX MAX MAX
<
> , then input objects is t2, finally,
if
132CC C
M
AX MAX MAX<>, then input object is t3. Note that this technique re-
quires the number of correlations equal to the number of patterns. In our simulation
the procedure of detection and classification based on the MSF, the POF, and the OF
requires 5 correlations for each target, whereas the method using the SDF filters re-
quires one correlation per a target.
We start of the design of the adaptive filter (AF) with assignment centers of classi-
fication regions in a unitary circle for t1, t2, and t3 (including distorted versions) as 0,
60, and 120 degrees respectively. Next, the proposed iterative algorithm is used. The
performance of the filter during the design process versus the iteration index is shown
in Fig. 3. The DC value of 0.9 was reached after 15 iterations. The correlation plane
obtained with the adaptive filter for the test scene is shown in Fig. 4. We can see
three sharp correlation peaks at locations of the targets. The phase information of the
correlation peaks correctly indicates classes of corresponding objects. The computer
simulation results are given in Table 1.
Table 1. Performance of correlation filters in terms of DC, number of correctly detected
classes, and complexity.
MSF
POF OF SDF
AF
DC
-0.9 -0.2 0.58 0.36 0.85
Number of correctly detected
classes
0 0 2 1 3
Number of required correlations 15 15 15 3 1
Line 1 provides the performance of each tested filter with respect to the DC. The
negative values of the DC indicate that a tested filter fails to recognize the target. The
classification performance of the filters is given in line 2 of Table 1. The computa-
tional complexity of the tested techniques in terms of required correlations is shown
204

in line 3 of Table 1. It can be seen that the proposed method yields the best perform-
ance with respect to detection, classification, and complexity. The AF adapts well to
patterns to be recognized and classified, and to a known background to be rejected.
Fig. 3. Performance of the adaptive SDF filter in the filter design process.
To guarantee statistically correct results, 30 statistical trails of the experiment for
different positions of the targets were performed. With 95% confidence, the DC of
the AF is equal to 0.85 ± 0.03, and the phase estimations at the origin of the correla-
tion peaks for t1, t2, and t3 are equal to 0±5 degrees, 60±4 degrees, and 120.5±2.5
degrees, respectively. This means that all targets can be reliably recognized and clas-
sified.
(a) (b)
Fig. 4. (a) Correlation plane for the test scene obtained with the adaptive filter, (b) normalized
intensity distribution.
205

5 Conclusions
A new method based on an adaptive approach and SDF filters was proposed to im-
prove recognition and classification of multiple targets embedded into a known clut-
tered background. It was shown that the proposed iterative algorithm generates an
adaptive filter, which is able to take control over whole correlation plane. With the
help of computer simulation, we showed that the proposed filters recognize and clas-
sify correctly distorted objects belonging to different classes.
References
1 B. V. K. Vijaya Kumar, L. Hassebrook: Performance measures for correlation filters. Appl,
Opt. 29 (1990) 2997-3006
2 C. S. Weaver, J. W. Goodman: Technique for optically convolving two functions. Appl.
Opt. 5 (1966) 1248-1249
3 H. J. Caulfield, W. T. Maloney: Improved discrimination in optical character recognition.
Appl. Opt. 8 (1969) 2354-2356
4 K. G. Leib, R. A. Bondurant, S. Hsiao, R.Wohlers, R. Herold: Aerial reconnaissance film
screening using optical matched-filter image-correlator technology. Appl. Opt. 17 (1978)
2892-2899
5 A. Vanderlugt, F. B. Rotz, A. Klooster, Jr.: Character-Reading by Optical Spatial Filtering.
In: J. T. Tippett, D. A. Berkowitz, L. C. Clapp, C. Koester, and A. Vanderburg, Jr., (eds.):
Optical and Electro-optical Information Processing, MTT Press, Cambridge (1965) 125-
141
6 Z. Bahri, B. V. K. Vijaya Kumar: Generalized synthetic discriminant functions. JOSA A 5
(1988) 562-571
7 B. Braunecker, R. Hauck, A. Lohmann: Optical Character Recognition Based on Nonre-
dundant Correlation Measurements. Appl. Opt. 18 (1979) 2746-2753
8 O. Billert, L. Singher: Adaptive multiple filtering. Opt. Eng. 41 (2002) 55-68
9 L. P. Yaroslavsky: The theory of optimal methods for localization of objects in pictures. In:
E. Wolf, (ed.): Pogress in Optics, Vol. XXXII, Elsevier North-Holland (1993) 145-201
10 J. L. Horner, P.D. Gianino: Phase-only matched filtering. Appl. Opt. 23 (1984) 812-816
11 C. F. Hester, D. Casasent: Multivariant technique for multiclass pattern recognition. Appl.
Opt. 19 (1980) 1758–1761
12 A. Mahalanobis, B. V. K. Vijaya Kumar, D. Cassasent: Minimum average correlation
filters. Appl. Opt. 26 (1987) 3633-3640
13 J. A. Gonzalez-Fraga, V. Kober, J. Alvarez-Borrego: Adaptive synthetic discriminant
function filter for pattern recognition. Opt. Eng. 45 (2006) 0570051-05700510
14 V. H. Diaz-Ramirez, V. Kober, J. Alvarez-Borrego: Pattern recognition with an adaptive
joint transform correlator. Appl. Opt. 45 (2006) 5929-5941
15 A. Vanderlugt: Signal detection by complex filtering. IEEE Trans. Inf. Theory 10 (1964)
139-145
206
