Ontology and E-Learning

Fabio Clarizia, Francesco Colace and Massimo De Santo

DIIIE – Università di Salerno, Via Ponte don Melillo, 1 I-84084, Fisciano (SA), Italy

Abstract. In the last decade the evolution on educational technologies forced

an extraordinary interest in new methods for delivering learning content to

learners. Distance education represents today an effective way for supporting

and sometimes substituting the traditional formative processes, thanks to the

technological improvements achieved in the field in recent years. However the

role of technology has often been overestimated and on the other hand the

amount of information students can obtain from the Internet is huge and they

can easily be confused. Teachers can also be disconcerted by this quantity of

contents and they are often unable to suggest the correct contents to their stu-

dents. In the open scientific literature, it is widely recognized that an important

factor of this success is related with the capability of customizing the learning

process for the specific needs of a given learner. This feature is still far to have

been reached and there is a real interest for investigating new approaches and

tools to adapt the formative process on specific individual needs. In this sce-

nario, the introduction of ontology formalism can improve the quality of forma-

tive process, allowing the introduction of new and effective services. Ontolo-

gies can lead to important improvements in the definition of courses knowledge

domain, in the generation of adapted learning path and in the assessment phase.

This paper provides an initial discussion of the role of ontologies in the context

of e-learning. We discuss such improvements related to the introduction of on-

tologies formalism in the E-Learning field and we present a novel algorithm for

ontology building through the use of Bayesian Networks. Finally, we show its

application in the assessment process and some experimental results.

1 Introduction

The development of adaptable and intelligent educational systems is widely consid-

ered one of the great challenges in scientific research. Among key elements for build-

ing advanced training systems, an important role is played by methodologies chosen

for knowledge representation. For example, the introduction of standardized tools for

defining a set of well-structured concepts can highly improve interoperability and

information sharing between complex systems. In literature, a set of concepts and

their relationships is commonly called ontology [1]. We can summarize the merits of

ontology as following: ontology provides a common vocabulary, and an explication

of what has been often left implicit. Obviously the systematization of knowledge and

the standardization is the backbone of knowledge within a knowledge-based system.

On the other hand a metamodel functionality specifies the concepts and relations

among them, which are used as the main building blocks. Ontology is one of the most

Clarizia F., Colace F. and De Santo M. (2007).

Ontology and E-Learning.

In Proceedings of the 4th International Workshop on Computer Supported Activity Coordination, pages 87-98

DOI: 10.5220/0002424400870098

 SciTePress

effective tools for formalizing the knowledge shared by groups of people. In the E-

Learning realm, ontology can easily manage the knowledge domain of a course and

allow a more detailed organization and adaptation of the learning path of students

[2][3]. Nevertheless, ontology building process is neither trivial nor easy [4]: “build-

ing ontologies is difficult, time consuming and expensive” [15]. Several researchers

have tried to justify a scientific way for developing ontologies. Perez and Benjamins

[30] propose design criteria and a set of principles that have been proved useful in the

development of ontologies: Clarity and Objectivity, Completeness, maximum mono-

tonic extensibility, Minimal ontological commitments, Ontological Distinction Prin-

ciple, Diversification of hierarchies, modularity, minimization of the semantic dis-

tance and standardization of names. These principles provide general guidelines for

the development of an ontology, which consists of Concepts, Relations, func-

tions/processes, axioms and instances. A “skeletal” methodology for building ontolo-

gies has been proposed and tested in [16]. This attempt to formalize the building

process through the definition of the following steps:

• Identify purpose

• Build ontology

o Ontology capture

o Ontology coding

o Ontology integration

• Evaluate ontology

• Document ontology

So we can define three sub-steps in the build ontology process [17]:

• Ontology capture: is the identification and definition of key concepts and re-

lationships in the domain of interest that refer to such concepts

• Ontology coding: deals with formalizing such definitions and relationships

in some formal language

• Ontology integration: deals with associating key concepts and terms in the

ontology with concepts and terms in the ontology with concepts and terms of

other ontologies; that is, incorporating concepts and terms from other do-

mains

According to the previous thoughts, the ontology building process is a craft rather

than engineering activity [28]. By way of illustration, let us discuss the common case

of the use of ontologies for representing the subjects of a course and the relationships

among them. When asked to describe their course, teachers regularly provide very

intricate ontologies representations, so having to manage that are neither easy to in-

terpret nor to use. Very often, relations among the concepts and their semantic values

look more similar to complex puzzles than to useful working tools. It is easy to imag-

ine the consequent difficulty in checking the validity of such descriptions. One way to

face the quoted problem is to make available to the user automated tools for building

and validating ontologies [5][6]. In literature many tools are available to accomplish

most aspects of ontology development. In particular much research has been carried

out to investigate the use of ontology to represent data. Source data can be stored in

an unstructured, semi-structured, or fully structured format (e.g. textual documents or

database schemata). Editing tools such as Protégé 2000 [18] and OILEd [19] have

been developed to help users create and edit ontology. However, it is a very difficult

and cumbersome task to manually derive ontology from data. Other approaches aim

to tackle this problem through the learning of ontology from free text [20], semi-

structured data (e.g., HTML or XML), or structured data from a database [21]. To

generate ontology from textual data, text processing techniques such as natural lan-

guage processing (NLP) combined with association rule mining [22], statistical mod-

eling [23], and clustering [24] have been applied to generate ontology. We have to

say that there are not any methodologies to use the huge structured data that are ac-

cumulated for a long time. In this paper, we propose an original method for ontology

building that can be applied to knowledge domain related to University Curricula. In

fact, many E-Learning systems are based on ontologies. Some papers describe an

authoring tool based on ontologies to [25] support the development of domain and

task ontologies and [26] support and perform (semi) automatic courseware authoring

activities. In particular the main assumption of this paper is that in such a context we

have a powerful source of evidence: the evaluation tests performed at the end of the

course. Usually, teachers design evaluation tests taking into careful account the se-

quencing and preparatory links of course subjects. So, in our opinion, those tests and

the answers given to them by students can be used to individuate the ontology of the

course. To this aim, we show how to use Bayesian Networks for easily mapping on-

tologies and present a novel algorithm for building “lightweight” ontologies through

them. Furthermore, we illustrate the application of this method in the assessment

phase. Namely, we realized a tool that builds the best assessment strategy according

to the information inferred by the analysis of questionnaires. The paper is organized

as follows: in Section 2 and 3, we give some details on ontologies and their mapping

through Bayesian Networks. In section 4 we describe the proposed approach for the

ontologies building process. In section 5 we provide the motivations and the details of

assessment tool based on ontology and Bayesian Networks. Finally, in the last section

we draw conclusions.

2 Ontology

The concept of ontology is originally taken from philosophy where it means a sys-

tematic explanation of being. In recent years, however, this concept has been intro-

duced and used in different contexts, thereby playing a predominant role in knowl-

edge engineering and in artificial intelligence [7]. In 1991, Neches stated that ontol-

ogy defines the basic terms and relations comprising the vocabulary of a topic area, as

well as the rules for combining terms and relations to define extensions to the vo-

cabulary [1]. Later on, Gruber, in the context of knowledge sharing, used the term to

refer to an explicit specification of a conceptualization [8]. Mizoguchi summarized

the merits of ontology as following: “Ontology provides a common vocabulary, and

an explication of what has been often left implicit”. According to Mizoguchi, the

systematization of knowledge and the standardization constitutes the backbone of

knowledge within a knowledge-based system. He also pointed out that a metamodel

functionality specifies the concepts and relations among them, which are used as the

main building blocks. Ontology engineering has contributed several interesting as-

pects to modelling. Maedche and Staab [27] stressed that ontologies could be consid-

ered as “metadata schemas providing a controlled vocabulary of concepts”. An inter-

esting clarification of the philosophical term ontology is provided by [29]. This paper

summarized several common definitions of ontology and tried to elaborate further the

main consideration that ontology is a specification of a conceptualization. According

to this approach ontology could be depicted as a philosophical discipline:

• An informal conceptual system

• A formal semantic account

• A specification of a “conceptualization”

• As a representation of a conceptual system via a logical theory

o characterized by specific formal properties

o characterized only by its specific purposes

• As the vocabulary used by a logical theory

• As a (meta-level) specification of a logical theory

In the field of computer science, ontology represents a tool useful to the learning

processes that are typical of artificial intelligence. In fact, the use of ontologies is

rapidly growing thanks to the significant functions they are carrying out in informa-

tion systems, semantic web and knowledge-based systems. The current attention to

ontologies paid by the AI community also arises from its recent interest in content

theories, an interest that is greater than the one in mechanism theories. In this regard,

Chandrasekaran [7] makes a clear distinction between these theories by asserting that,

though mechanisms are important since they are proposed as the secret of making

intelligent machines, they can not do much without a good content theory of the do-

main on which they have to work. Besides, once a good content theory is available,

many different mechanisms can be used to implement effective systems, all using

essentially the same content. Following this point of view, ontologies are content

theories, since their principal contribution consists in identifying specific classes of

objects and relations existing in some knowledge domains [9]. Ontological analysis,

therefore, clarifies knowledge structures: given a domain, its ontology represents the

heart of any knowledge representation system for that domain. Another reason for

creating and developing ontology is the possibility of sharing and reusing knowledge

domain among people or software agents. In general, ontology is a complex structure

made up of a series of elements, each of which is composed of a kind of Relation and

a series of related Concepts. An ontology in the context of e-learning means hat we

admit the presence of an (unspecified) conceptual system, which we may assume to

underlie a particular knowledge base. This is the common hypothesis in E-Learning

implementations. For example, as far as concerning University Courses, by means of

an ontology built by the teacher, it will be possible to describe the knowledge do-

main, the subjects constituting it, the relations among the various subjects, as well as

methodologies and means with which they are presented. These explicit specifica-

tions help users to understand what specific terms signify in a given domain [2] and

reduce terminological and conceptual ambiguity. The content of an ontology depends

both on the amount of information and on the degree of formality that is used to ex-

press it. Generally, we distinguish two main types of ontologies: lightweight and

heavyweight [3]. A lightweight ontology is a structured representation of knowledge,

which ranges from a simple enumeration of terms to a graph or taxonomy where the

concepts are arranged in a hierarchy with a simple (specialization, is-a) relationship

between them. Heavyweight ontology adds more meaning to this structure by provid-

ing axioms and broader descriptions of the knowledge. In this paper, we will adopt

the lightweight approach keeping in mind this definition of ontology: “ontology may

take a variety of forms, but it will necessarily include a vocabulary of terms and some

specification of their meaning. This includes definitions and an indication of how

concepts are inter-related which collectively impose a structure on the domain and

constrain the possible interpretations of terms” [10]. In the next section we will show

an approach to the representation of ontology by the use of Bayesian networks for-

malism.

2.1 Ontology and Bayesian Networks

As previously said in this section, we will describe how Bayesian Networks can be

used “to map” and “to represent” an ontology. Bayesian Networks have been success-

fully used to model knowledge under conditions of uncertainty within expert systems,

and methods have been developed from data combination and expert system knowl-

edge in order to learn them [11]. Bayesian Networks represent a “hot” topic in the

research field; the interested reader can find some interesting good surveys in [12],

[13]. In this paper a key role is played by the learning process of Bayesian Networks.

It has two important advantages: firstly, it is easy to encode knowledge of an expert

and such knowledge can be used to improve learning efficiency and accuracy. Sec-

ondly, nodes and arcs of the learned Bayesian network are recognizable links and

causal relationships. So users can understand and exploit more easily the knowledge

encoded in the representation. A Bayesian network is a graph-based model encoding

the joint probability distribution of a set of random variables X

{ ,..., }XX

. It is

composed by:

• A directed acyclic graph S (called structure) where each node is associated

with one random variable

and each arc represents the conditional de-

pendence among the nodes that it joints

• A set P of local probability distributions, each of which is associated with a

random variable

and conditioned by the variables corresponding to the

source nodes of the arcs entering the node with which

is associated. The

lack of an arc between two nodes involves conditional independence. On the

other hand, the presence of an arc from the node

to the node

repre-

sents that

is considered a direct cause of

Given a structure S and the local probability distributions of each node

p|()X

where

represents the set of parent nodes of

, the joint probability distribution

()X

is obtained from:

() ( | )

XpXPa

∏

and it is evident that the couple (S, P) encodes

p()X

unequivocally (on the hypothesis of conditional independence of the

given

the

) [11].

In order to build a Bayesian Network for a given set of variables, we have to de-

fine some arcs from the causal states to the other ones that represent their direct ef-

fects obtaining a network that accurately describes the conditional independence

relations among the variables. The aim of this paper is the introduction of an algo-

rithm, based on the formalism of the Bayesian networks, able to infer the

propaedeutic relationships among different subjects (in other terms the ontology)

belonging to the knowledge domain of a university curricula. The first step of this

algorithm is the introduction of a mapping between Ontology and Bayesian Network.

In our ontology model, nodes represent the subjects belonging to the knowledge do-

main (the course) while the arcs mean a propaedeutic relationship among the nodes.

We can map this ontology graph in a Bayesian Network in the following way: the

Bayesian Network nodes model the subjects belonging to the course Knowledge

Domain and the knowledge of subject by students while arcs in the same way mean

the propaedeutic relationships among the nodes. Given the previous mapping strat-

egy, our aim is to define the ontology used by teacher in his/her course. Obviously,

we must define data type and data set for this approach. As previously said, student’s

answers to the evaluation tests represent a source of implicit evidence. In fact, teach-

ers through the end-of-course evaluation tests not only assess student’s knowledge for

every subject, but describe the course ontology and outline the propaedeutic aspects

that relate subjects each other. On the basis of these considerations, teachers have

designed the final test of the first-level course on Computer Science at the Engineer-

ing Faculty of the University of Salerno and the final test of the first-level course on

Introduction to Computer Science at the Languages Faculty of the University of

Salerno. We must outline that this process was very long and hard for teachers. The

result of this process is shown in Figure 1. Each node of the networks has two states

and shows the probability that a generic learner knows the subject associated with the

same node. We supposed that each node can assume only the following two states

(random Bernoullian variable): state ‘Yes’: complete knowledge of the subject and

state ‘Not’: total ignorance on the subject. The student level of knowledge could be

evaluated on the basis of the answers given to the questions (a set of questions is

proposed for each subject).

Ontology #2

Ontology #1

Ontology #3

Fig. 1. Proposed ontology for the first-level course on Computer Science (Ontology #1)

and Introduction to Computer Science (Ontology #2 and Ontology #3).

3 An Algorithm for Ontology Learning

As previously said, the teacher has difficulties sketching the relationships among the

course subjects and their propaedeutic connections. A source of indirect evidence that

can be employed for reconstructing“a-posteriori” ontology can be represented by the

end-of-course evaluation tests. On the basis of the ontology presented in Figure 1,

some multiple-choice questionnaires have been realized. The previously described

graph represents the ontologies, but can also be used as a Bayesian Network for the

inference process. The student’s level of knowledge is evaluated on the basis of the

answers given to the questions. The presence of missing values, in other words the

state of some variable can not be observable, has not been foreseen. This hypothesis

can be obtained imposing that the student have answer to all the questions and con-

sidering a missing answer as a wrong one. Through a process of Bayesian inference

conducted on the previously described networks, the candidate ontologies have been

learned from data. The inference algorithm used in our experiments is the one called

“junction-tree” introduced by Finn V. Jensen in [14]. For the inferential process, we

have used data coming from five hundred questionnaires for the first ontology and

three hundred questionnaires for the second and third ones. So, we have to estimate

the strength of propaedeutic relationship between two arguments after the learning of

the network. The presence of an arc between two nodes in the Bayesian network can

be interpreted as the existence of a causality relationship between the variables asso-

ciated to the same nodes. It is important to define a function able to evaluate this

strength. For the nodes that belong to a Bayesian network a good dependence indica-

tor is the cross-entropy function so defined:

∑

bPaP

baP

baPBAEC

)()(

),(

log),(),.(.

where A and B are nodes of the Bayesian network and a and b are the states of each

node. According to cross entropy definition, we can say that A and B are independent

if and only if C.E.(A, B) is equal to 0. However, often we do not have the real prob-

ability distribution of the full network but only an empirical evaluation of it coming

from data analysis. In this sense, it is incorrect to consider as condition of independ-

ence C.E.(A,B) = 0 and we can suppose A independent from B when C.E.(A,B)<e,

where e>0 is an arbitrary threshold near to zero. The cross entropy function can also

quantify the dependency weight between the nodes. In fact, an high value of

C.E.(A,B) means a very strong preparatory relation between the two nodes. In order

to suppose that at least the father-child nodes links proposed by the teacher is correct,

we submitted the data coming from the questionnaires to statistical tests, typical of

Bayesian network structural learning algorithms that are able to establish from them

the correct father-child nodes arrangement. This tests result confirmed that the ar-

rangement proposed by teachers is correct. After this validation, we set as input to the

Bayesian network the data coming from the questionnaires in order to obtain the

probability values associated to the various states of the nodes. With these values we

calculated the cross entropy values among all the single states of the net. Namely, the

cross entropy has been calculated not only for the arcs proposed by the teacher but

also for all the brother nodes.

Figure 2 shows the obtained results. On the left side of the Figure, we can see the

cross entropy values for the correct arcs that represent propaedeutic connection be-

tween two topics, while on the right side (after the blank column) we can see the

cross entropy values for the incorrect arcs. In general, we can say that the arcs desig-

nated by teachers show a greater cross entropy values than other arcs so to confirm

the teacher ontology design. We want also outline that in the case of ontology #1, an

arc P(8|6) having a cross entropy value in the range of correct arcs is reported. Given

that examined data show the existence of a significant value of cross entropy between

these nodes the teacher, according this model, has to refine his original ontology

proposal.

a) Ontology #1

b) Ontology #2

c) Ontology #3

Fig. 2: (a,b,c) Obtained Results on reference set ontologies.

4 An Assessment Tool based on the Ontology Framework

In this section, we will describe in detail the architecture of an assessment tool based

on ontology framework previously described. We designed our tool keeping in mind

the main needs of students and teachers. From a technological point of view we de-

signed the tool according these constraints: Web based approach - Aesthetic and

minimalist design - Flexibility and efficiency of use - Help users recognize, diagnose,

and recover from errors. In the first phase of the designing we pointed out the actors

of the system and the use cases. We identified three typologies of actors in the sys-

tem: Administrators, Teachers and Students. Each of these figures has a well defined

role and tasks. In particular Administrators can introduce new courses, describe new

ontologies and manage the accesses to the tool. Teachers can design the reference

ontology, describe the learning objects and the questions linked to the nodes of ontol-

ogy. Teachers can also manage the reports of every student in order to better super-

vise the learning process. Students can use tool in three different ways: Exam, Nor-

mal test, Bayesian test. In the Exam way our tool arranges a classical final test exam

according to the teacher’s strategy. In particular teacher can choose the question’s

number for every subject and the scoring for every question. At the end of the exam

the system produces a report analyzing the performance of student in every subject.

The normal test approach can be used during some module of the course. In particular

it can help student to learn better the various learning objects.

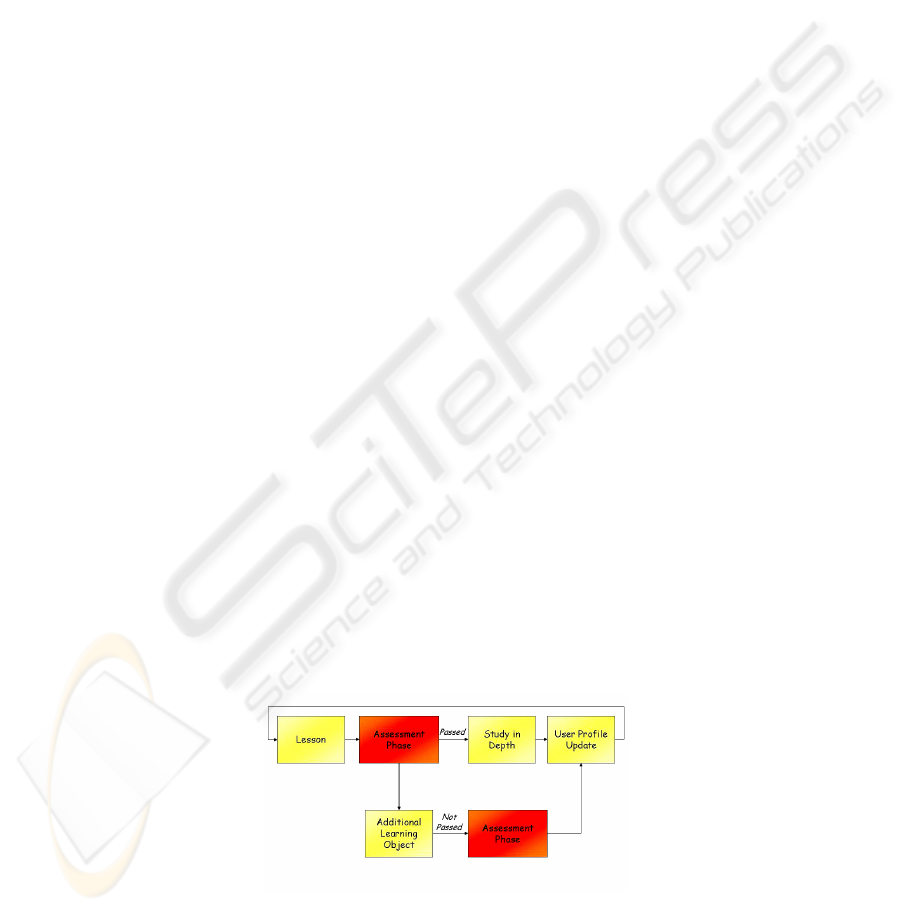
The more interesting service offered by our tool is the Bayesian test. This service

makes the most of the matching between ontology and Bayesian network. In fact the

first step is the introduction of a mapping strategy between Ontology and Bayesian

Network. In our ontology model nodes represent the subjects belonging to the knowl-

edge domain of the course and the arcs mean a preparatory relationship among the

nodes. In this way we can map the ontology graph in a Bayesian network in the fol-

lowing way: the nodes of Bayesian Network model the subjects belonging to the

course. The states (two: yes and not) of nodes represent the knowledge of student in

the subject. The arcs mean the propaedeutic relationships among the nodes. In other

words a node of Bayesian network-ontology represents the Knowledge domain of a

course and quantizes student’s knowledge of this node. First of all the system select a

set of questions associated to every network node. At the end of this first phase sys-

tem, through a Bayesian approach infers what subjects the students knows better than

others. In fact through the Bayesian analysis the system can measure the percentage

of correct answer in a subject. In particular it can predict the percentage of correct

answer to a subject after a correct (or not) answer to questions related to propaedeutic

subjects. At this point it can apply various strategies: for example it can select and

propose to the student the question with the smaller percentage of correct answer. At

the end of Bayesian test a detailed report on the knowledge of student in the various

subjects is sent to teacher and to student himself. In particular after the Bayesian test

the system proposes to the student some learning object for deepening some subjects.

At the same time tool proposes to the teacher a periodic report with the analysis of

performances of various students in every subject. In this way teacher can understand

easily where students need more help. At the end of Bayesian Test the system up-

dates the user profile of students and builds its new adapted learning path of the full

course. The system updates also the values of ontology’s links according to the

method introduced in this paper.

5 Experimental Results

In order to test the effectiveness of our tool we used it during the course of Introduc-

tion to Computer Science at Foreign Literature and Language Faculty of University of

Salerno. This course is composed by seven modules: Introduction to PC Architecture,

Introduction to Operative System, Microsoft Word, Microsoft Excel, Microsoft Ac-

cess, Microsoft Power Point, and Internet. The organization of every module and is

depicted in figure 3.

Fig. 3. Organization of every module.

On the basis of the considerations of previous section, teacher designed the refer-

ence ontology. Each node of the networks has two states and shows the probability

that a generic learner knows the subject associated with the same node. We have

supposed that each node can assume only the following two states (random Bernoul-

lian variable): state ‘Yes’: complete knowledge of the subject and state ‘Not’: total

ignorance on the subject. The student level of knowledge could be evaluated on the

basis of the answers given to the questions (a set of questions is proposed for each

subject). At the ends of the course students have to get through a final examination’s

test composed by forty questions. The questions belong to every subject of knowl-

edge domain. The number of student’s course was about 50 and at the starting of the

course we arranged them in two groups (named blue and red). The first group had a

classical support to course activities and used only the normal test approach while the

second one used also all functionalities of the tool as didactic support. At the begin-

ning of the course teachers designed every module’s ontology in order to organize the

contents and an assessment test. The results are in the table 1. The aim of this test is

to allow a first description of student through a metadata structure. In this way teach-

ers can obtain information about the initial knowledge level of students. This infor-

mation is very useful in order to describe for the first time the student profile. At this

point the system organized for the student of red group a support material for every

module of course. In particular it selects the most suitable contents through a match-

ing between the metadata of learning objects and the description of the student. As

previously said during the course the students of the two groups attended to the les-

sons and used the virtual teacher tool. In particular students of red group at the end of

every module sustained a Bayesian Test. At the end of course students had their final

course exam. In the tables we depicted the results:

Table. 1. Results of Assessment Tool. The meaning of range are: [0-10]: inadequate, [11-15]:

poor progress, [16-20]: adequate, [21-25]: good, [26-30]: very good.

Blue Group Red Group

Assessment Test Students Assessment Test Students

0-10 10 0-10 12

11-15 11 11-15 10

16-20 9 16-20 8

21-25 3 21-25 3

26-30 3 26-30 2

Total 36 Total 35

Table. 2. Results of Final Test.

Blue Group Red Group

Final Test Students Final Test Students

0-10 4 0-10 3

11-15 9 11-15 5

16-20 8 16-20 6

21-25 10 21-25 12

26-30 5 26-30 9

Total 36 Total 35

If we analyze the difference between the assessment and the final exam (table 1

and 2) we can note that the percentage of students that get through the assessment test

is 37% in the red group and 42% in the blue group while in the case of the final ex-

amination the percentage is 77% in the red group and 64% in the blue group. We can

note as more students of red group get through the final exam and improve their per-

formance respect the assessment test (about 40%). In particular we can note that the

students of the blue group have a minor improvement (about 22%) than the students

of the red group. At the same time the percentage of red group’s students that have a

mark in the range 26-30 is higher than in the case of blue group: 26% to 8%. In order

to collect more information about the effectiveness of our tool at the end of course we

submitted a questionnaire to every student. In the questionnaire we asked the effec-

tiveness of Bayesian test and of learning objects furnished by system at the end of the

test. The 87 % of students said that the support of Virtual Teacher tool was very im-

portant in the learning process. In particular the 73% of students declared that the

supporting learning object helped them in a better knowledge of the various subjects.

6 Conclusions

In this paper, we have presented a method for learning curricula ontologies. In par-

ticular, our approach is based on Bayesian networks. Thanks to their characteristics,

these networks can be used to model and evaluate the conditional dependencies

among the nodes of ontology on the basis of the data obtained from student tests. An

experimental evaluation of the proposed method has been performed using real stu-

dent data. We integrated the proposed method in a tool for the assessment of students

during a learning process. This tool is based on the use of ontology and Bayesian

Network. In particular through the matching between ontology and Bayesian Network

our tool allow an effective tutoring and a better adaptation of learning process to

demands of students. The assessment based on Bayesian approach allows as deeper

analysis of student’s knowledge.

References

1. Neches R., Fikes R. E., Finin T., Gruber T. R., Senator T., Swartout W. R., Enabling Tech-

nology for Knowledge Sharing, AI Magazine, 12(3):36-56, 1991

2. Uschold M., Gruninger M., Ontologies: Principles, Methods and Applications, Knowledge

Engineering Review, volume 11, number 2, June 1992.

3. Gomez-Perez, A.; Corcho, O., Ontology languages for the Semantic Web, Intelligent Sys-

tems, IEEE Volume 17, Issue 1, Jan/Feb 2002 Page(s):54 – 60

4. Staab, S., Schnurr, H. P., Studer, R. Sure, Y., Knowledge Processes and Ontologies, IEEE

Intelligent Systems 16(1), January/Febrary 2001

5. Guarino, N., Welty, C., Evaluating ontological decisions with OntoClean, Communications

of the ACM, 45(2), 2002

6. Fernandez-Lopez, M., Gomez-Lopez, A., Pazos-Sierra, A., Building a Chemical Ontology

Using METHONTOLOGY and the Ontology Design Environment, IEEE Intelligent Sys-

tems and their applications,1999

7. Chandrasekaran, B., Josephson, J.R., Benjamins, R., What are ontologies, and why do we

need them?, IEEE Intelligent Systems, 14(2), 1999

8. Gruber, T.R, Translation approach to portable ontology specification, Knowledge Acquisi-

tion 5, 1993

9. Maedche A., Staab S., Ontology Learning for the Semantic Web, IEEE Intelligent Systems,

vol. 16 no. 2, Mar/Apr 2001, 72-79

10. Uschold M., R. Jasper, A Framework for Understanding and Classifying Ontology Appli-

cations, IJCAI99 Workshop on Ontologies and Problem Solving Methods, Stockholm, 1999.

11. Heckermann, D., Bayesian Networks for Data Mining, Journal of Knowledge Discovery

and Data Mining 1(1), Kluwer Academic Publishers, 1997

12. Singh, M., Valtorta, M., Construction of Bayesian Network Structures from Data: a Brief

Survey and an Efficient Algorithm, International Journal of Approximate Reasoning, 12, 1995

13. Heckerman, D., Geiger, D., Chickering, D., Learning Bayesian Network: the Combination

of Knowledge and Statistical Data, Machine Learning, 20, 1995

14. Jensen, F., An Introduction to Bayesian Networks, Springer – Verlag, New York, 1998

15. Gruninger, M, Lee, J., “Ontology applications and Design”, Introductory article to a special

issue on Ontology Engineering, Communications of the ACM, 45(2), 42-47, February,

2002

16. Uschold M., King M., Towards a methodology for building ontologies, IJCAI95, Montreal,

1995

17. R. Prieto Diaz, A faceted approach to building ontologies, Information Reuse and Integra-

tion, 2003. IRI 2003. IEEE International Conference on , 27-29 Oct. 2003, On page(s):

458- 465

18. N. Noy and D. L. McGuinness, Ontology Development 101: A Guide to Creating Your

First Ontology Dept. Mech. Ind. Eng., Univ. Toronto, Toronto, ON, Canada, Rep. SMI-

2001-0880, 2001.

19. S. Bechhofer, I. Horrocks, P. Patel-Schneider, and S. Tessaris, “A proposal for a descrip-

tion logic interface,” in Proc. Int.Workshop Description Logics, 1999, pp. 33–36.

20. A. Maedche and S. Staab, “Mining ontologies from text,” EKAW-2000—12th International

Conference on Knowledge Engineering and Knowledge Management. Juan-les-Pins,

France, LNAI, Springer, 2000.

21. A. Doan, J. Madhavan, P. Domingos, and A. Y. Halevy, “Learning to map between ontolo-

gies on the semantic web,” in Proc. 11th Int.World Wide Web Conf. (WWW2002), Hono-

lulu, HI, 2002, pp. 662–673.

22. A. Maedche and S. Staab, “Ontology Learning for the SemanticWeb,” IEEE Intell. Syst.

(special issue on the semantic web), vol. 16, no. 2, pp. 72–79, Mar.–Apr. 2001.

23. A. Faatz and R. Steinmetz, “Ontology enrichment with texts from the WWW,” in Proc.

Semantic Web Mining Second Workshop (ECML/PKDD-2002), Finland, 2002.

24. G. Bisson and C. Nedellec, “Designing clustering methods for ontology building: the Mo’K

workbench,” in Proc. 14th Eur. Conf. Artificial Intelligence Workshop Ontology Learning

(ECAI’00), S. Staab, A. Maedche, C. Nedellec, and P. WiemerHasting, Eds., Germany, 2000.

25. Aroyo, L., et al , 2002 (1). A layered approach towards domain authoring support, Interna-

tional Conference on Artificial Intelligence (ICAI’02), Las Vegas, USA.

26. Aroyo, L., et al, 2002 (2). Courseware authoring tasks ontology, International Conference

on Computers in Education (ICCE’02), Auckland, New Zealand.

27. Maedche, A. and S. Staab (2001). “Ontology learning for the semantic web”, IEEE Intelli-

gent Systems, Vol 16, No 2, pp: 72-79.

28. Gruber, T. R. (1995). 'Towards principles for the design of ontologies used for knowledge

sharing', International Journal of Human-Computer Studies Vol 43, no 5/6, pp: 907- 928.

29. Guarino N. and P. Giareta (1995). 'Ontologies and knowledge bases: Towards a termino-

logical clarification', In Mars, N., Editor, IOS Press, p. 25-32.

30. Perez and Benjamins (1999), 'Overview of Knowledge Sharing and Reuse Components:

Ontologies and Problem-Solving Methods', In the Proceedings of IJCAI-99 Workshop on

Ontologies and Problem-Solving Methods (KRR5), Stockholm, Sweden.