
On the Relationship between Confidentiality Measures:
Entropy and Guesswork
Reine Lundin, Thijs Holleboom and Stefan Lindskog
Department of Computer Science
Karlstad University, Sweden
Abstract. In this paper, we investigate in detail the relationship between entropy
and guesswork. The aim of the study is to lay the ground for future efficiency
comparison of guessing strategies. After a short discussion of the two measures,
and the differences between them, the formal definitions are given. Then, a redef-
inition of guesswork is made, since the measure is not completely accurate. The
change is a minor modification in the last term of the sum expressing guesswork.
Finally, two theorems are stated. The first states that the redefined guesswork is
equal to the concept of cross entropy, and the second states, as a consequence of
the first theorem, that the redefined guesswork is equal to the sum of the entropy
and the relative entropy.
1 Introduction
Computer security is a branch of computer science, where the goal is to protect enti-
ties from being unauthorized tampered with. The three most well-known goals in the
field are confidentiality, integrity, and availability. Confidentiality is the prevention of
unauthorized disclosure of information, integrity is the prevention of unauthorized mod-
ification of information, and availability is the prevention of unauthorized withholding
of information or resources. Collectively they are known as ”CIA”.
A key problem with computer security is that it is hard to measure and therefore
hard to evaluate. In many situations we have not even agreed on, or defined, generally
accepted security attributes [1], making it impossible to measure security since we do
not know what to measure on. Furthermore, when we actually have agreed on defi-
nitions for security attributes, like in the common criteria [2], the measures are often
qualitative, i.e., based on experience, and do not carry enough information about its
values to allow formal analysis. Hence, quantitative security measures are desirable,
making it possible to perform an analytical and more exact description of security.
Two proposed, quantitative confidentiality measure are entropy [3] and guesswork
[4,5]. Entropy is the famous and classical security measure of uncertainty that originally
was suggested by Shannon in 1944. He defined it as the average amount of information
of a random variable. Guesswork, on the other hand, gives the minimum expected num-
ber of guesses in an optimal brute force attack. The relationship between entropy and
guesswork has been under consideration for a while, and a connection has only been
found in terms of bounds [4, 5].
Lundin R., Holleboom T. and Lindskog S. (2007).
On the Relationship between Confidentiality Measures: Entropy and Guesswork.
In Proceedings of the 5th International Workshop on Security in Information Systems, pages 135-144
DOI: 10.5220/0002426901350144
Copyright
c
SciTePress

In this paper, the relationship between entropy and guesswork is investigated in
detail. After a redefinition of guesswork, since the measure is not completely accurate,
the relationship or result is stated in two theorems. The first theorem states that the
redefined guesswork is equal to the concept of cross entropy, and the second theorem
states, as a consequence of the first theorem, that the redefined guesswork is equal to
the sum of the entropy and the relative entropy.
The rest of the paper is organized as follows. In Section 2, guessing strategies for
entropy and guesswork is presented. The relationship between entropy and guesswork
is investigated in Section 3. Finally, Section 4 concludes the paper.
2 Entropy, Guesswork, and Guessing
Guessing the correct value of a random variable X, can be seen as a game of two
players. Player one chooses a secret value from a given set of possible values, and
player two tries to guess the correct value, using a strategy. From the known information
about the game, such as the probability distribution of the search space or conditions
of the guessing process, a set of strategies or actions, are possible. In the continuation,
the probability distribution of the search space is assumed to be known. Furthermore,
from the set of strategies we normally want to use an optimal guessing strategy, that
minimizes the needed number of questions to find the value of X. This is the focus of
game theory [6], i.e., how to best play the game.
In order to compare the efficiency between different strategies, possibly having dif-
ferent information about the game, measures that give the expected number of guesses
to find the correct value are needed. Two such measures are entropy and guesswork.
Entropy gives the minimum number of expected questions, when we have the possibil-
ity to ask questions of the form Q
1
=”Is X ∈ A?”, for any set A of the search space. A
variant of this question, that for example is used in the bisection method to find a root
of a continuous function in an interval, is ”Is X > a?”. Guesswork, on the other hand,
gives the minimum expected number of questions when we have the possibility to ask
questions of the form Q
2
=”Is X = x
i
?”.
For guesswork, the optimality (minimum number of questions) comes from the fact
that we can arrange the probabilities of the values x
i
in non-increasing probability order,
and then start testing them. For entropy, the optimality comes from the fact that entropy
gives the minimum average code length for compression [7], and that a sequence of yes
or no questions is equivalent to a binary code. A way to construct such a set of optimal
questions is to use the Huffman algorithm [7]. In the following, we use guesswork and
entropy for both the name of the measure and the optimal strategy that is connected to
the measure.
The difference between guesswork and entropy resides in the information of the
two questions, Q
1
and Q
2
. For Q
1
we are allowed to group several values into a set
of values, and test if the correct value is in that set. For Q
2
we are only allowed to
test one value at a time. Hence, Q
1
uses the divide and conquer strategy, binary search,
and Q
2
uses the one at a time strategy, linear search. Furthermore, Q
2
is actually a
special case of Q
1
, since Q
2
can be rewritten as ”Is X ∈ A = {x
i
}?” for any set
136
A of the search space. This indicates that entropy is always smaller than (or equal to)
guesswork, something that will be obvious in the next section.
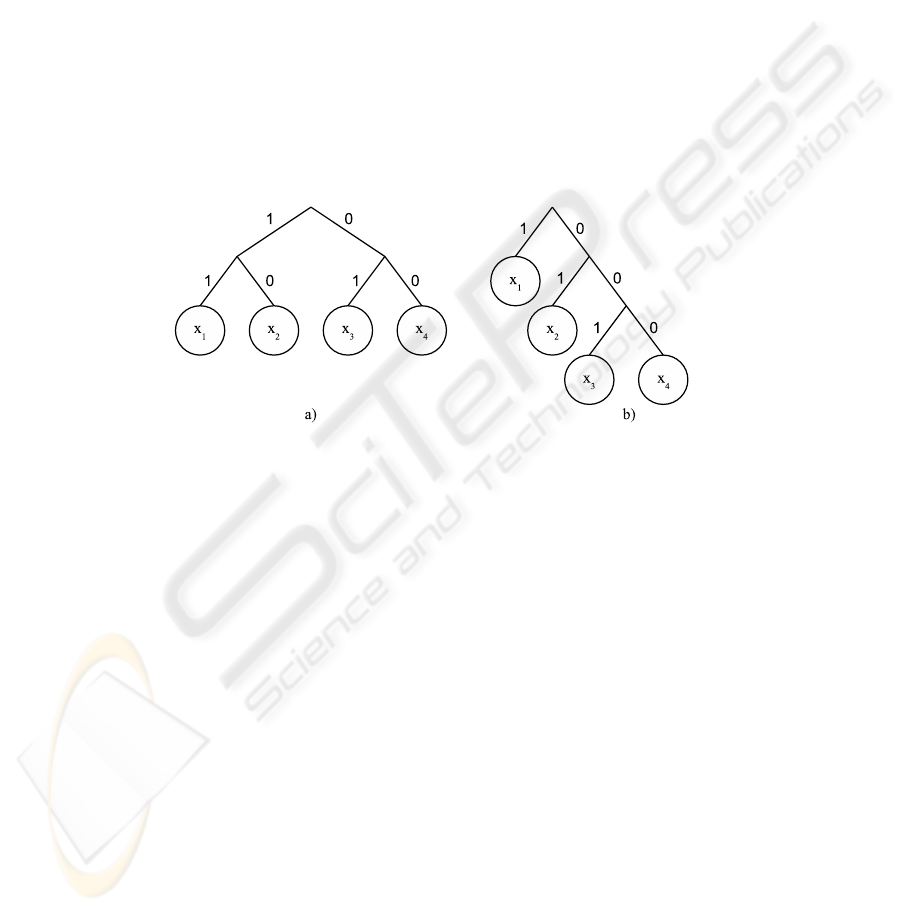
When searching for the correct value, the chosen strategy gives rise to a search
tree. This is illustrated in Fig. 1 when we have the search space χ = {x
1
, x
2
, x
3
, x
4
}
with the probabilities p(x
1
) = 0.4, p(x
2
) = 0.2, p(x
3
) = 0.2, and p(x
4
) = 0.2. The
search tree for entropy (using Huffman) is shown in a), with codes x
1
= 11, x
2
= 10,
x
1
= 01, and x
4
= 00, and for guesswork in b), with codes x
1
= 1, x
2
= 01,
x
1
= 001, and x
4
= 000. To make things more clear, the first question for entropy is
”Is X ∈ A = {x
1
, x
2
}?” , and the first question for guesswork is ”Is X = x
1
?”. This is
the same, in both cases, as to ask ”Is the first bit set to one?”. This procedure continues
with the second bit, and so on, until the correct value is found. In Fig. 1, we also see how
entropy and guesswork balances the search tree. Entropy balances the tree by dividing
the remaining probabilities as equal as possible between the branches, while guesswork
creates the tree totally unbalanced. This is similar to the behaviours of binary and linear
search.
Fig.1. The search tree for a) entropy, using Huffman, and b) guesswork.
3 The Relationship between Entropy and Guesswork
In this section, background information as well as formal definitions of information
entropy, relative entropy, cross entropy and guesswork is given. Then, a minor mod-
ification in the definition of guesswork is made, since the measure is not completely
accurate. Finally, two theorems are stated. The first theorem states that the redefined
guesswork is equal to the concept of cross entropy, and the second theorem states, as
a consequence of the first theorem, that the redefined guesswork is equal to the sum of
the entropy and the relative entropy.
3.1 Background
In [4], Massey showed that a trivial upper bound for guesswork in terms of entropy does
not exist. He showed this, by using an infinite probability distribution where guesswork
becomes arbitrary large, while at the same time entropy tends to zero. Pliam in his PhD
thesis [5], argued that due to this entropy may not be a good measure of guessability for
137

brute force attacks. Instead, he proposed the use of guesswork, or a measure based on
variational distance, as new possible measures of guessability.
As Massey in [4], the authors in [8] presented a slightly different example to show
the same. Let the probability distribution be, p
1
= 1 − b/n and p
2
= . . . = p
n
=
b/(n
2
− n). Then W (p) = 1 + b/2, constantly, and H(p) → 0, when n → ∞. Hence,
again we have a distribution where guesswork can become arbitrary large, while the
entropy tends to zero.
Even though guesswork does not have an upper bound in terms of entropy, Massey
[4] showed that guesswork, however, has a lower bound in terms of entropy
2
H(p)−2
+ 1 ≤ W (p) (1)
when H(p) ≥ 2. This result were derived by using standard calculus of variation to find
that a geometric probability distribution maximizes the entropy for a constant value of
the guesswork.
3.2 Formal Definitions
In this subsection the formal definitions of information entropy, relative entropy, cross
entropy and guesswork is given.
Information Entropy. Information or Shannon’s entropy [3], often simply referred
to as entropy, is the classical measure of uncertainty that was originally suggested by
Shannon in 1944. He defined it as the average amount of information from a discrete
random variable.
Definition 1. The entropy H(p) of a probability distribution p = (p
1
, . . . , p
n
) is de-
fined as
H(p) = −
n
X
i=1
p
i
log
2
(p
i
) (2)
It is assumed that the higher the entropy of a random variable is, the harder it is on the
average to guess its value. This is an assumption that has shown to be inconsistent with
guesswork [4,5]. The maximum value of the entropy, with no boundary conditions,
is obtained for the uniform probability distribution u, and H(u) = log
2
(n), [7]
1
. In
computer science and information theory the base of the logarithm is taken to be two,
measured in bits, and in mathematics and physics the base is taken to be e, measured in
nats.
Relative Entropy. The relative entropy [7], or Kullback Leibler distance, measures the
distance between two probability distributions. It can be interpreted as a measure of
inefficiency, since it gives the extra number of bits if a code of an arbitrary distribution
is used than the ”true” distribution.
1
To verify this, set p
i
=
1
n
and calculate the sum.
138

Definition 2. The relative entropy D(p||q) between two probability distributions p =
(p
1
, . . . , p
n
) and q = (q
1
, . . . , q
n
) is defined as
D(p ||q) =
n
X
i=1
p
i
log
2
p
i
q
i
(3)
The relative entropy is always non-negative and zero iff p = q. Note that the relative
entropy is not a true distance, since it is not symmetric and does not satisfy the triangular
inequality.
Cross Entropy. From information theory, we also have the concept of cross entropy
[9] between two probability distributions.
Definition 3. The cross entropy H(p, q) for two probability distributions p = (p
1
, . . . , p
n
)
and q = (q
1
, . . . , q
n
) is defined as
H(p, q) = −
n
X
i=1
p
i
log
2
(q
i
) (4)
Cross entropy can be seen as a generalization of entropy to other distribution, and if
p = q cross entropy is equal to entropy.
Guesswork. Guesswork [4, 5] is a measure that gives the minimum expected number
of guesses to find the value of X, when we are only allowed to test one value at a time.
This is equal to an optimal brute force. In an optimal brute force attack the attacker has
complete knowledge of the probability distribution of X, and can, thus, arrange and
start testing the values of X in a non-increasing probability order, according to
p
1
≥ p
2
≥ . . . ≥ p
n
≥ 0 (5)
The crack package [10] for UNIX passwords orders the potential passwords in a similar
way.
Definition 4. Guesswork W (p) for a probability distribution p = (p
1
, . . . , p
n
), ar-
ranged according to (5), is defined as
W (p) =
n
X
i=1
ip
i
(6)
The higher the guesswork of a random variable is, the harder it is on the average to
guess its value. The maximum value, with no boundary conditions, is obtained for the
uniform probability distribution u, and W(u) =
n+1
2
, [5]
2
.
2
To verify this, set p
i
=
1
n
and calculate the sum.
139
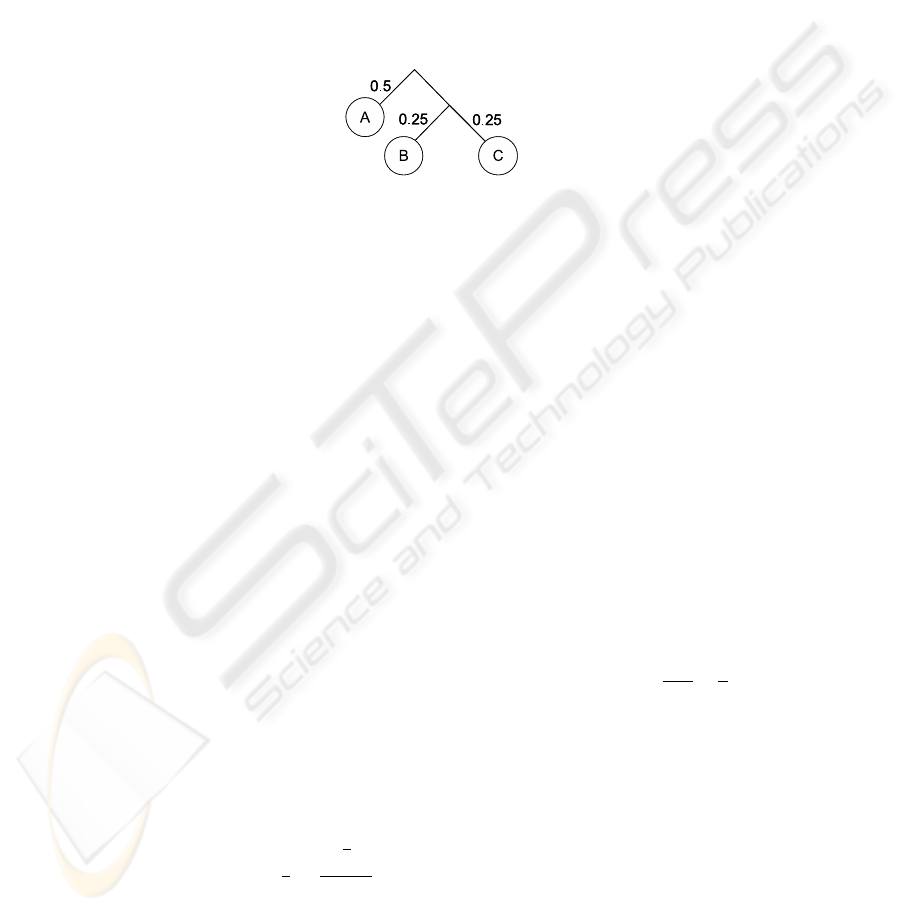
3.3 Redefinition of Guesswork
From equation (6) in definition 4, guesswork, the last term in the sum is weighted with
n. This is, however, not completely accurate, since the last guess in the guessing process
discriminate the last two values of the random variable. That is, if the answer to the last
question is ”yes” then the correct value is x
n−1
, and the search finishes. If instead the
answer is ”no”, the correct value is x
n
, and the search finishes. For example, if we have
p(A) = 0.5 and p(B) = p(C) = 0.25, then W (p) = 1.75. However, as illustrated
in Fig. 2, on average it is enough to make 1.5 guesses. In half of the times, it will be
Fig.2. An example of a guessing tree, with p(A) = 0.5 and p(B) = p(C) = 0.25.
sufficient to use one guess to find the correct value, and in the other half it will be
sufficient to use two guesses. This is why we redefine guesswork, with the last term in
the sum weighted with n − 1, grouping the last two probabilities together.
Definition 5. Let the probability distribution p be arranged according to (5). Then
guesswork W (p) is defined as
W (p) =
n
X
i=1
r
i
p
i
(7)
where
r
i
=
i if i < n
n − 1 if i = n
(8)
By using the same arguments as in [5], the maximum value of the redefined guess-
work is obtained for the uniform distribution u, and its value is W (u) =
n+1
2
−
1
n
. Note
that, when n → ∞, the maximum value of the redefined guesswork and the guesswork
is equal. More generalized, when n → ∞, redefined guesswork is equal to guesswork,
since then r
i
= i.
In Fig. 3, we have for the same probability distribution as in section 3.1, p
1
= 1 −
b/n and p
2
= . . . = p
n
= b/(n
2
− n), plotted the redefined guesswork and guesswork
for different values of n, when b = 10. The uppermost line is the guesswork, with a
constant value of W (p) = 1 +
b
2
, and the line below is the redefined guesswork, with
a value of W (p) = 1 +
b
2
−
b
n(n−1)
. Notice in the figure how the redefined guesswork
narrows guesswork as n increases.
140

10 20 30 40 50 60 70 80 90 100
5.9
5.91
5.92
5.93
5.94
5.95
5.96
5.97
5.98
5.99
6
n
W
Fig.3. Redefined guesswork and guesswork for the probability distribution
p
1
= 1 − 10/n and p
2
= . . . = p
n
= 10/(n
2
− n).
3.4 Redefined Guesswork and Cross Entropy
In this section, we show that the redefined guesswork is indeed a special case of cross
entropy.
Theorem 1. The redefined guesswork W (p) is equal to cross entropy H(p, r),
where r = (2
−r
1
, . . . , 2
−r
n
), i.e.,
W (p) = H(p, r) (9)
Proof. First note that r = (2
−r
1
, . . . , 2
−r
n
) is a probability distribution since
n
X
i=1
2
−r
i
=
n−1
X
i=1
2
−r
i
+ 2
−(n−1)
(10)
= 1 − 2
−(n−1)
+ 2
−(n−1)
= 1
By using equations (7) and (10), we get
W (p) =
n
X
i=1
r
i
p
i
(11)
= −
n
X
i=1
p
i
log
2
(2
−r
i
)
= H(p, r)
where the last step is according to definition 3.
141

3.5 Redefined Guesswork and Entropy
Now, we are in a position to state the theorem connecting the redefined guesswork,
entropy, and relative entropy.
Theorem 2. The redefined guesswork W (p) is equal to the sum of entropy H(p) and
relative entropy D(p ||r), where r = (2
−r
1
, . . . , 2
−r
n
), i.e.,
W (p) = H(p) + D(p ||r) (12)
Proof. By standard calculus cross entropy is equal to the sum of entropy and relative
entropy.
H(p, q) = −
n
X
i=1
p
i
log
2
(q
i
) (13)
= −
n
X
i=1
p
i
log
2
(q
i
) +
n
X
i=1
p
i
log
2
(p
i
) −
n
X
i=1
p
i
log
2
(p
i
)
= H(p) +
n
X
i=1
p
i
log
2
(
p
i
q
i
)
= H(p) + D(p||q)
Hence,
W (p) = H(p, r) (14)
= H(p) + D(p||r)
according to equation (13) and Theorem 1.
Theorem 2, is actually a special case of a theorem showing that entropy gives the
minimum expected length of codes. That is, H(p) ≤ L(p) =
P
i
p
i
l
i
, where l
i
is the
length of the code word with probability p
i
. In the theorem, W (p) is changed to L(p),
since guesswork can be seen as a special case of expected code length, with l
i
= r
i
. If
instead guesswork would have been used, l
i
= i, we would have get
W (p) = H(p) + D(p ||q) − log
2
(
n
X
i=1
2
−i
) (15)
where q =
2
−i
i
2
−i
. Note that when, n → ∞, equation (15) and (12) is equal.
InFig. 4, we have plotted the redefined guesswork, entropy, and relative entropy for
the probability distribution p
1
= 1−b/n and p
2
= . . . = p
n
= b/(n
2
−n), when b = 4.
In the figure, by observation, superposition of H(p) and D(p ||r) becomes W (p).
4 Conclusion and Future Work
We have in this paper investigated in detail the relationship between the two probabilis-
tic confidentiality measures entropy and guesswork. After a redefinition of guesswork,
142

5 10 15 20 25 30 35 40 45 50
0
0.5
1
1.5
2
2.5
3
3.5
D(p||r)
W(p)
H(p)
n
Fig.4. The redefined guesswork, entropy, and relative entropy for the probability distribution
p
1
= 1 − 4/n and p
2
= . . . = p
n
= 4/(n
2
− n).
since the originally proposed measure is not completely accurate, we formally proved
that the redefined guesswork is equal to the sum of the entropy and the relative entropy.
We hope that result of the paper is a further step towards a better understanding of the
similarities and differences between these measures.
The goal of our future work is to compare the efficiency between the different guess-
ing strategies, entropy and guesswork. Another goal is to identify under which circum-
stances the different confidentiality measures should be used. We believe that the choice
of measure is dependent on the considered attack model, since the amount of informa-
tion an attacker has will affect the number of guesses. Furthermore, we hope to derive
a formula for the rate of the guesswork, that is connected to the rate of the entropy, and
hence continue to examine the confidentiality levels for selectively encrypted messages
[11].
References
1. Lindskog, S., Jonsson, E.: Adding security to QoS architectures. In Burnett, R., Brunstrom,
A., Nilsson, A.G., eds.: Perspectives on Multimedia: Communication, Media and Informa-
tion Technology. John Wiley & Sons (2003) 145–158
2. Common Criteria Implementation Board: Common criteria for information technology se-
curity evaluation, version 3.1. http://www.commoncriteriaportal.org/ (2006)
3. Shannon, C.E.: Communication theory of secrecy systems. Bell System Technical Journal 28
(1949) 656–715 Reprinted in Claude Elwood Shannon: Collected papers. Edited by N. J. A.
Sloan and A. D. Wyner, IEEE Press, 1993.
4. Massey, J.: Guessing and entropy. In: Proceedings of the 1994 IEEE International Symp. on
Information Theory. (1994) 204
143

5. Pliam, J.O.: Ciphers and their Products: Group Theory in Private Key Cryptography. PhD
thesis, University of Minnesota, Minnesota, USA (1999)
6. Myerson, R.B.: Game Theory: Analysis of Conflict. Harvard University Press (1997)
7. Cover, T., Thomas, J.: Elements of Information Theroy. John Wiley & Sons (1991)
8. Malone, D., Sullivan, W.: Guesswork is not a substitute for entropy. In: Proceedings of the
Information Technology & Telecommunications Conference. (2005)
9. Brown, P.F., Pietra, S.D., Pietra, V.D., Lai, J.C., Mercer, R.L.: An estimate of an upper bound
for the entropy of english. Computational Linguistics 18 (1992) 31–40
10. Muffett, A.D.E.: Crack: A sensible password checker for UNIX (1992)
11. Lundin, R., Lindskog, S., Brunstrom, A., Fischer-Hbner, S.: Using guesswork as a measure
for confidentiality of selectively encrypted messages. In Gollmann, D., Massacci, F., Yaut-
siukhin, A., eds.: Quality of Protection: Security Measurements and Metrics. Volume 23.
Springer (2006) 173–184
144
