Reliability Estimation for Multimodal Error Prediction

and Fusion

Krzysztof Kryszczuk, Jonas Richiardi and Andrzej Drygajlo

Swiss Federal Institute of Technology Lausanne (EPFL)

Signal Processing institute (STI-ITS-LIDIAP)

Abstract. This paper focuses on the estimation of reliability of unimodal and

multimodal veriﬁcation decisions produced by biometric systems. Reliability es-

timates have been demonstrated to be an elegant tool for incorporating quality

measures into the process of estimating the probability of correctness of the deci-

sions. In this paper we compare decision- and score-level schemes of multimodal

fusion using reliability estimates obtained with two alternative methods. Further,

we propose a method of estimating the reliability of multimodal decisions based

on the unimodal reliability estimates. Using a standard benchmarking multimodal

database we demonstrate that the score-level reliability-based fusion outperforms

alternative approaches, and that the proposed estimates of multimodal decision

reliability allow for an accurate prediction of errors committed by the fusion mod-

ule.

1 Introduction

Reducing error rates of biometric authentication systems is a challenging enterprise.

High-quality biometric signals are difﬁcult to acquire, the behavioral characteristics of

the users of biometric systems contribute to the intra-class variability of features, and

the biometric traits are not stationary over time. As a result, classiﬁcation errors are

inevitable. Therefore it is necessary that next to the actual binary decision, the system

produce an estimate of decision reliability. The reliability of a decision is the level of

trust that one can have in its correctness [1, 2]. This level of trust, or degree of belief

is given by a single event probability according to the subjective Bayesian interpreta-

tion [3]. Probabilistic output characterizes statistical classiﬁcation methods that operate

on Bayes’ rule [4]. Any system that compares a sample to previously estimated prob-

abilistic distributions of other samples’ features is able to return a conﬁdence measure

[5] in terms of posterior probability. However, simple calculation of posterior probabil-

ity does not allow an inclusion of quality measures, which have been demonstrated to

supply identity-independent information that fosters improved robustness to adverse en-

vironments [6, 7, 1]. Also, appropriately trained neural networks can output scores that

have been shown to be equivalent to posterior probabilities [8], but it is difﬁcult to as-

sign a probabilistic interpretation to the processes inside the network. An intuitive way

for estimating decision reliability is based on analyzing the margins [9] - the absolute

Kryszczuk K., Richiardi J. and Drygajlo A. (2007).

Reliability Estimation for Multimodal Error Prediction and Fusion.

In Proceedings of the 7th International Workshop on Pattern Recognition in Information Systems, pages 15-24

DOI: 10.5220/0002431100150024

 SciTePress

difference between the dichotomizer’s accuracy in choosing one class over another ob-

served on a development set. However, the use of margin-based conﬁdence estimation

does make use of signal quality measurements. In [1] a probabilistic method of com-

puting reliability estimates allows for an easy incorporation of quality measures. The

output of the estimate is in probabilistic terms. The reliability estimates have been ap-

plied to perform decision-level multimodal fusion (face and speech)[10]. The method of

reliability estimation was based on Bayesian networks. A conceptually related method

based on explicit distribution modeling with Gaussian Mixture Models (GMM) was

demonstrated to accurately predict face veriﬁcation errors [2]. The main difference be-

tween the two approaches is that the dependence relationships between the variables are

not pre-deﬁned during the GMM model construction, like it is in the case of Bayesian

networks. Instead, those relationships are implicitly learned from the data in the train-

ing phase. In this paper we provide a comparison of the two alternative methods of

reliability estimation using a benchmark multimodal biometric database BANCA [11].

The comparison includes also an alternative method of conﬁdence estimation that has a

probabilistic interpretation: margins [9].

In [10] the reliability estimates are applied to perform a fusion of unimodal deci-

sions in a multimodal biometric veriﬁcation scenario. In this paper we propose a score-

level multimodal fusion scheme based on reliability estimates. We demonstrate that the

proposed fusion scheme outperforms the decision gating method, for both BN- and

GMM-based reliability estimators. We also show that the application of reliability es-

timators for multimodal fusion allows to achieve lower error rates than corresponding

fusion schemes based on the alternative conﬁdence measure. Since the discussed meth-

ods are probabilistic in nature, in this work we do not include comparisons with existing

heuristic methods of integrating quality measures in the fusion process [6,7].

Further, we propose a method of computing a multimodal reliability estimate using

the unimodal reliability estimates. We show that thus obtained multimodal reliability

estimate can be used to accurately predict multimodal classiﬁcation errors in similar

fashion as in the unimodal setting.

This paper is structured as follows: Section 2 deﬁnes the basic concepts of reliability

and introduces the proposed schemes of multimodal fusion using reliability, as well as

a scheme of fusion of reliability estimates. Section 3 gives the details of the criteria and

experimental design for evaluation, Sections 4 and 5 contain the results of the reported

experiments, with a discussion in Section 6. We conclude the paper in Section 7.

2 Reliability and Multimodal Fusion

2.1 Evidential Reliability

Reliability R of a classiﬁer decision D(x) for an observation x is deﬁned as a condi-

tional probability of the event ”the classiﬁer made a correct decision”, given supporting

evidence E [10]. Since reliability is estimated for each individual observation x, it can

be considered as a function of D(x):R(D(x)) = P (D(x) = 1|E = e(x)), where

D(x) = 1 if the decision is correct and D(x) = 0, otherwise. An instance e(x) of

evidence E may consist of measures derived from the score, feature or signal levels

in the classiﬁcation process. In the experiments reported here, for both modalities the

evidence vector was e(x) = [S

(x), qm

(x)], where S

(x) and qm

(x) are nor-

malized score and signal quality measure relevant to x. For details on reliability and

evidence the reader is referred to [1, 10, 2]. Reliability estimation is a tool designed for

the purpose of labeling decisions as reliable or unreliable for further processing. La-

beling of decision D(x) is performed by comparing the reliability estimate R(D(x))

to a reliability threshold, the minimal accepted value of the belief in the correctness of

the decision D(x). Without explicit labeling, the reliability estimates can be effectively

used for multimodal fusion.

2.2 Multimodal Fusion

For each given decision D(x), a matching score S

and an associated reliability esti-

mate R

is available. We propose to perform multimodal fusion using the reliability

measures, following the formula:

m=1

, (1)

where n is the number of unimodal systems used (in our case n = 2) , R

and S

denote the respective reliability estimate and the unimodal classiﬁcation output (score)

for given modality m. In the case of decision level fusion, the output S

≡ D is a

binary decision: S

≡ D ∈ −1, 1. For score-level fusion, S

is the normalized out-

put of the classiﬁer’s discriminant function. Scores from different classiﬁers are often

expressed in incompatible scales, therefore there is a need of normalization before per-

forming the score-level fusion. In our work we used the z-normalization scheme [7].

In the case of decision-based fusion, the binarization of the scores eliminates the need

for normalization. The decision based on the fused output is made by comparing the

value of S

to a threshold that minimizes the Half-Total Error Rate (HTER) [9] on a

development dataset.

2.3 Fusion of Reliability Estimates

It is usually not possible to apply the reliability estimation scheme to directly esti-

mate the reliability of multimodal decisions: this would require that the fused classiﬁers

would make mistakes for the very same presentations. Since that is in general not the

case, the number of models for all possible error conﬁgurations would grow geometri-

cally with the number of classiﬁers involved. Training all these models would require

amounts of available training data beyond what is usually available in reality. In this

situation is is important to be able to derive multimodal reliability estimates from the

unimodal estimates, which are not as data-demanding.

Out of all present unimodal scores, any and all can be correct, or wrong. Therefore

the unimodal reliability estimates are combined into a multimodal estimate as follows:

R (D

) = R (D

∪ D

∪ ... ∪ D

) (2)

In the case of two fused modalities (n = 2), the multimodal reliability is expressed

R (D

) = R (D

∪ D

) = R (D

) + R (D

) − R (D

) · R (D

) . (3)

and D

are assumed to be independent, considering that they originate from dif-

ferent modalities. This is a simplifying assumption - dependencies between modalities

may occur, and in this case the product R(D

) · R(D

) would have to be replaced by a

more accurate estimate of R(D

∩ D

3 Experimental Design and Evaluation Criteria

3.1 Databases and Experimental Design

In our experiments we used face images and speech data from the BANCA database,

English part. The BANCA database contains data collected from a pool of 52 individ-

uals, 26 males and 26 females. For the details on the BANCA database and associated

evaluation protocol the reader is referred to [11].

In the experiments presented in this paper we adhered strictly to the open-set pro-

tocol P, which involves training the classiﬁcation models using ’clean’ data recorded

in the controlled conditions, and testing them in the controlled as well as deteriorated

conditions. The protocol P deﬁnes that all database data are to be sub-divided into two

datasets, g1 and g2. While data from one dataset is used for user model training and

testing, the other dataset (a development set) may be used for parameter tuning. In ac-

cord with this directive, we use the development set to adjust the decision thresholds

for the test set, but also to train the reliability estimation models.

The unimodal protocol P strictly deﬁnes the assignment of user data to the genuine

access or impostor access pools. We respect this assignment and in order to do so we

reduce the amount of client face data to one per access (as opposed to the available

ﬁve) in order to match the amount of speech data at hand. in this way we maintain

the compatibility with the P protocol and at the same time we overcome the problems

related to the use of the chimerical databases [12]. In accordance with the BANCA

gudelines, all error rates shown in Table 1 are reported separately for g1 and g2, and

then their average is computed.

3.2 Unimodal Classiﬁers and Quality Measures

The face and speech data from the BANCA database consists of data collected in three

different recording conditions: controlled, degraded and adverse. For each of the record-

ing conditions, four independent recording sessions were organized, making a total of

12 sessions.

For face data, the faces in the images were cropped out and normalized geometri-

cally (aligned eye positions) and photometrically (histogram normalization). The face

veriﬁcation was performed using the extracted DCTmod2 features and a Bayesian clas-

siﬁer with Gaussian Mixture Models (GMM) [13]. For each face image, a quality mea-

sure qm was derived by computing a correlation with the average face template [2]. The

average face template was computed on the respective development dataset.

The BANCA database provides a large amount of speech data per user: 2 ﬁles per

session (about 20 s each) x 2 microphones x 12 sessions. In our case, we used only the

data from microphone 1.

The speaker veriﬁcation system used is based on the Alize toolkit [14]. The Al-

ize speech/pause detector is run to remove silence portions of the input speech signal

before feature extraction. Features used are 12 MFCCs with delta and acceleration co-

efﬁcients, and cepstral mean normalisation. A world model is trained from the pooled

clean training data of all clients, using 200 diagonal covariance-matrix Gaussian com-

ponents. Each client’s model is then adapted (means only) with their own recordings

using MAP adaptation. The quality measure used for speech is related to the signal-to-

noise ratio, computed using energy-based voice activity detection [15].

3.3 Evaluation Criteria

The potential of each compared method to discard unreliable and therefore potentially

erroneous decisions is evaluated according to the following criteria [2]:

– the accuracy of decisions labeled as reliable must be monotonically growing, and

– the number of discarded decisions must be kept at a minimum.

Since labeling the decisions as reliable or unreliable is a result of reliability-based

decision thresholding, we analyze the properties of different reliability estimators as a

function of the reliability threshold. Those properties are, in accordance with the cri-

terion given above, accuracy of the classiﬁer (in the terms of 1-HTER) after having

discarded decisions labeled as unreliable, and the number of decisions labeled as reli-

able for the given reliability threshold value, relative to the total number of decisions.

Since we wish these properties to be maximized simultaneously, we also analyze their

product which we refer to as a ’Performance Measure’ [2]. This property helps establish

at which level of reliability the system achieves highest accuracy while keeping most

decisions.

First, we evaluate the unimodal reliability estimates, then we apply them to multi-

modal fusion as discussed in Section 2. Finally, we perform a fusion of the reliability

estimates and evaluate them in a similar fashion as it was the case with unimodal relia-

bility estimates. In each case, we provide a comparison with the corresponding results

obtained using the method of classiﬁer conﬁdence estimation based on the margins [9].

4 Unimodal Reliability - Experimental Evaluation

In this section we present the experimental results of reliability estimation for the uni-

modal classiﬁers operating on the face and speech modalities. For each modality, we

consider following reliability estimators: explicit GMM-based reliability estimator R-

GMM [2], Bayesian Network-based reliability estimator R-BN [1], conﬁdence esti-

mates derived from the margin information M [9].

4.1 Face Modality- Error Prediction

Figure 1 shows the properties of various reliability estimators applied to the classiﬁer

operating on the face modality, for datasets g1 and g2, in terms of accuracy gain (1-

HTER), relative number of decisions remaining after reliability thresholding, and the

relative performance measure.

0 0. 2 0. 4 0. 6 0. 8 1

100

R eliability Threshold

Accuracy [% ]

0 0. 2 0. 4 0. 6 0. 8 1

100

R eliability Threshold

R elative Decisions Left [% ]

0 0. 2 0. 4 0. 6 0. 8 1

-20

100

R eliability Threshold

P erformance Measure

R -GMM

R -BN

Margins

R -GMM

R -BN

Margins

R -GMM

R -BN

Margins

(a)

0 0. 2 0. 4 0. 6 0. 8 1

100

R eliability Threshold

Accuracy [% ]

0 0. 2 0. 4 0. 6 0. 8 1

100

R eliability Threshold

R elative Decisions Left [% ]

0 0. 2 0. 4 0. 6 0. 8 1

-20

100

R eliability Threshold

P erformance Measure

R -GMM

R -BN

Margins

R -GMM

R -BN

Margins

R -GMM

R -BN

Margins

(b)

Fig.1. Error prediction and decision reject/accuracy gain tradeoff, face, a.: dataset g1, b.: dataset

g2.

4.2 Speech Modality- Error Prediction

Figure 2 shows the properties of various reliability estimators applied to the classiﬁer

operating on the speech modality, for datasets g1 and g2, in terms of accuracy gain (1-

HTER), relative number of decisions remaining after reliability thresholding, and the

relative performance measure.

5 Multimodal Reliability - Experimental Evaluation

5.1 Multimodal Fusion

The results of the fusion experiments in terms of accuracy (1-HTER) are collected in

Table 1. Next to the results of reliability and margin- based fusion, results of oracle

fusion (disjunction of binary accuracies of unimodal classiﬁers), and mean rule fusion

are presented for comparison.

0 0. 2 0. 4 0. 6 0. 8 1

100

R eliability Threshold

Accuracy [% ]

0 0. 2 0. 4 0. 6 0. 8 1

100

R eliability Threshold

R elative Decisions Left [% ]

0 0. 2 0. 4 0. 6 0. 8 1

R eliability Threshold

P erformance Measure

R -GMM

R -BN

Margins

R -GMM

R -BN

Margins

R -GMM

R -BN

Margins

(a)

0 0. 2 0. 4 0. 6 0. 8 1

100

R eliability Threshold

Accuracy [% ]

0 0. 2 0. 4 0. 6 0. 8 1

100

R eliability Threshold

R elative Decisions Left [% ]

0 0. 2 0. 4 0. 6 0. 8 1

R eliability Threshold

P erformance Measure

R -GMM

R -BN

Margins

R -GMM

R -BN

Margins

R -GMM

R -BN

Margins

(b)

Fig.2. Error prediction and decision reject/accuracy gain tradeoff, speech. a.: dataset g1, b.:

dataset g2.

5.2 Error Prediction

The results presented in Table 1 show that score-based fusion schemes outperform their

decision-based counterparts for fusion methods based on both reliability estimates and

margins. Therefore, in further analysis of the reliability of decisions after fusion we take

into account only score-based fusion results. In this section, we analyze how well dif-

ferent reliability estimates help predict recognition errors. We use the error prediction

curves for this purpose. The fusion reliability estimates are obtained using Equation 3.

The results are plotted in Figure 3(a) for the dataset g1 and (b) for the dataset g2, in

terms of accuracy gain (1-HTER), relative number of decisions remaining after relia-

bility thresholding, and the relative performance measure.

6 Discussion of the Experimental Results

6.1 Unimodal Reliability

The unimodal results for face show that all considered reliability measures can be used

to predict classiﬁer errors, and to discard unreliable decisions. While the properties of

all reliability estimators are comparable for the face data, dataset g1, in the case of g2

the margin-derived conﬁdence measure fails to provide adequate error prediction. This

results shows that margin-based conﬁdence measures are very sensitive to the dataset-

dependent shifts in score distributions. Reliability estimators R-GMM and R-BN al-

lowed to obtain error-free classiﬁcation for both g1 and g2 dataset, by choosing the

value of the reliability threshold equal or close to 1.

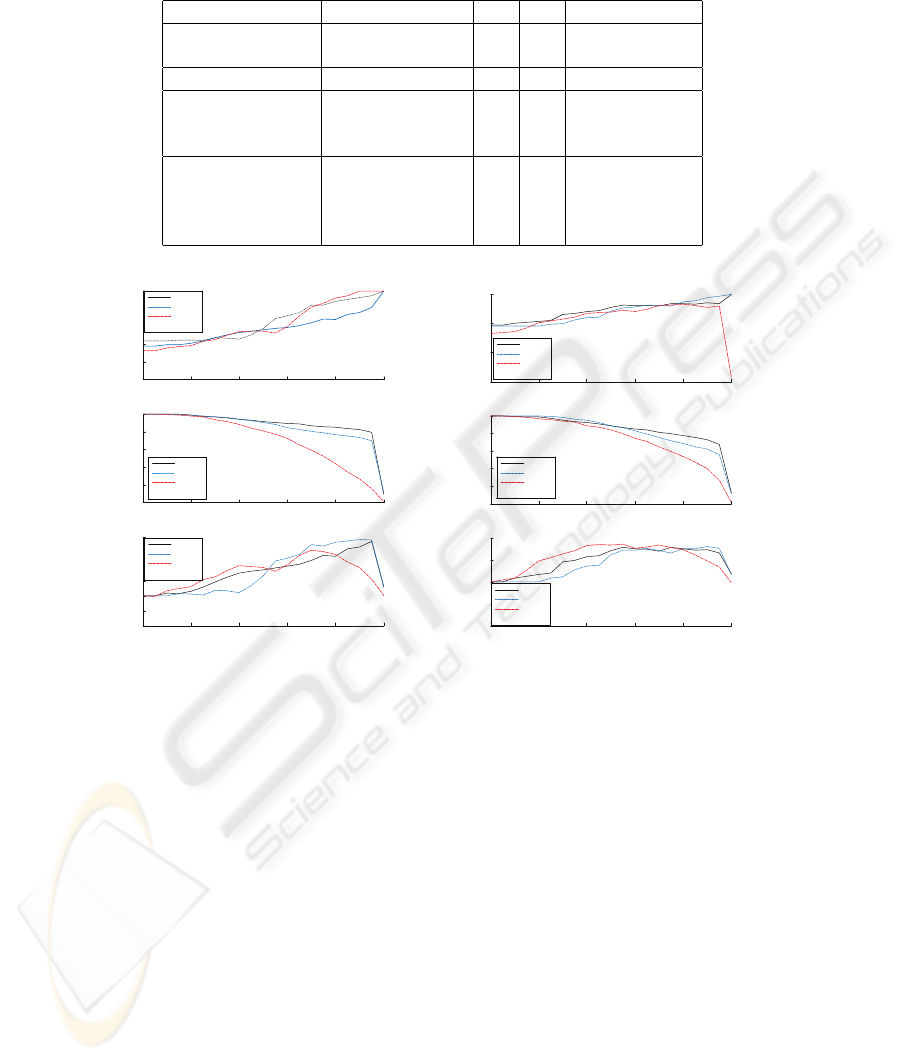
Table 1. Results of multimodal fusion experiments.

Fusion method g1 g2 average (g1+g2)/2

Unimodal systems Face 0.754 0.782 0.768

Speech 0.923 0.92 0.922

Reference fusion Oracle 0.982 0.974 0.978

Decision-level fusion Margins 0.904 0.911 0.908

Reliability, R-GMM 0.932 0.943 0.938

Reliability, R-BN 0.927 0.935 0.931

Score-level fusion Margins, M 0.928 0.931 0.929

Reliability, R-GMM 0.942 0.947 0.945

Reliability, R-BN 0.941 0.938 0.938

Mean rule 0.938 0.928 0.933

0 0. 2 0. 4 0. 6 0. 8 1

100

R eliability Threshold

Accuracy [% ]

0 0. 2 0. 4 0. 6 0. 8 1

100

R eliability Threshold

R elative Decisions Left [% ]

0 0. 2 0. 4 0. 6 0. 8 1

-20

-10

R eliability Threshold

P erformance Measure

R -GMM

R -BN

Margins

R -GMM

R -BN

Margins

R -GMM

R -BN

Margins

(a)

0 0. 2 0. 4 0. 6 0. 8 1

100

R eliability Threshold

Accuracy [% ]

0 0. 2 0. 4 0. 6 0. 8 1

100

R eliability Threshold

R elative Decisions Left [% ]

0 0. 2 0. 4 0. 6 0. 8 1

-40

-20

R eliability Threshold

P erformance Measure

R -GMM

R -BN

Margins

R -GMM

R -BN

Margins

R -GMM

R -BN

Margins

(b)

Fig.3. Error prediction and decision reject/accuracy gain tradeoff, fusion. a.: dataset g1, b.:

dataset g2.

6.2 Multimodal Fusion

The multimodal fusion results show that the application of reliability measures R-GMM

and R-BN in fusion results in higher accuracy than using margin-based approach or

mean/sum rule. We expect that for databases containing more degraded conditions (the

speech degradation in the BANCA database in particular is not very pronounced), the

difference would be more signiﬁcant since the signal quality is explicitly taken into ac-

count. The score based fusion schemes proved to outperform decision-based algorithms

using both margin and reliability estimates. This result can be explained by the fact that

during a decision-based fusion information coming from a less reliable classiﬁer is lost.

The R-GMM reliability estimation scheme based on explicit GMM models granted best

performance on the tested data. This result can be attributed to the difference in proba-

bilistic modeling between R-GMM and R-BN methods, as discussed in Section 1.

6.3 Multimodal Reliability

For both datasets g1 and g2, the accuracy gains in terms of (1-HTER) for the R-

GMM, R-BN and M reliability estimates were comparable. However, the application

of margin-based estimates resulted in a dramatic decrease in the number of decisions

considered reliable, for similar accuracy. This fact is reﬂected in the dropping shape of

the corresponding curve in the performance plots for g1 and g2. The presented results

show that R-GMM and R-BN methods are best suited for the estimation of reliability

of multimodal fusion decisions, and that their performance meets the evaluation criteria

deﬁned in Section 3.3.

7 Conclusions

The lead idea of this work was to demonstrate that reliability measures can be effec-

tively used for error prediction in uni- and multimodal biometric veriﬁcation applica-

tions. The presented results show that reliability estimates allow for eliminating poten-

tially erroneous decisions based on collected evidence. We have presented a method of

performing probabilistic fusion of the multimodal reliability estimates. Proposed meth-

ods was proven to allow for accurate error prediction of multimodal decisions.

The results of the experimental evaluation suggest that both methods of reliability

estimation based on the Bayesian networks R-BN, and on the explicit GMM model-

ing R-GMM, perform similarly in terms of their error prediction power. Insigniﬁcantly

better results of R-GMM for fusion may hint at the exploitation of the intra-modal de-

pendencies by the R-GMM method.

Margin-based conﬁdence estimates proved to perform not as well as the reliability

measures on the tasks of uni- and multimodal error prediction and multimodal fusion.

This outcome can be explained by the fact that, unlike reliability estimates R-GMM

and R-BN, margin-based conﬁdence estimators do not allow for an inclusion of quality

measures.

Acknowledgements

This work was partially funded by grants within the framework of the Swiss National

Science Foundation (SNSF) and National Centre of Competence in Research (NCCR)

Interactive Multimodal Information Management IM2 research projects.

References

1. Richiardi, J., Drygajlo, A., Prodanov, P.: Conﬁdence and reliability measures in speaker

veriﬁcation. Journal of the Franklin Institute 343 (2006) 574–595

2. Kryszczuk, K., Drygajlo, A.: On combining evidence for reliability estimation in face veri-

ﬁcation. In: Proc. of the EUSIPCO 2006, Florence (2006)

3. Russel, S., Norvig, P.: Artiﬁcial Intelligence. A Modern Approach. Prentice Hall (1995)

4. Duda, R., Hart, P., Stork, D.: Pattern Classiﬁcation. 2nd edn. Wiley Interscience, New York

(2001)

5. Bengio, S., Marcel, C., Marcel, S., Mariethoz, J.: Conﬁdence measures for multimodal iden-

tity veriﬁcation. Information Fusion 3 (2002) 267–276

6. Toh, K.A., Yau, W.Y., Lim, E., Chen, L., Ng, C.H.: Fusion of auxiliary information for multi-

modal biometrics authentication. In: Proceedings of International Conference on Biometrics.

Lecture Notes in Computer Science, Hong Kong, Springer (2004) 678–685

7. Fierrez-Aguilar, J.: Adapted Fusion Schemes for Multimodal Biometric Authentication. PhD

thesis, Universidad Politecnica de Madrid (2006)

8. Campbell, W., Reynolds, D., Campbell, J., Brady, K.: Estimating and evaluating conﬁdence

for forensic speaker recognition. In: Proc. IEEE Int. Conf. on Acoustics, Speech, and Signal

Processing (ICASSP). Volume 1. (2005) 717–720

9. Poh, N., Bengio, S.: Improving fusion with margin-derived conﬁdence in biometric authen-

tication tasks. In: Proceedings of the AVBPA, Rye Brook NY, USA (2005)

10. Kryszczuk, K., Richiardi, J., Prodanov, P., Drygajlo, A.: Error handling in multimodal bio-

metric systems using reliability measures. In: 13th European Signal Processing Conference

(EUSIPCO 2005), Antalya, Turkey (2005)

11. Bailly-Baillire, E., Bengio, S., Bimbot, F., Hamouz, M., Kittler, J., Marithoz, J., Matas, J.,

Messer, K., Popovici, V., Pore, F., Ruiz, B., Thiran, J.P.: The BANCA database and eval-

uation protocol. In Kittler, J., Nixon, M., eds.: Proceedings of 4th Int. Conf. on Audio-

and Video-Based Biometric Person Authentication (AVBPA). Volume LNCS 2688. (2003)

625–638

12. Poh, N., Bengio, S.: Can chimeric persons be used in multimodal biometric authentication

experiments? In: Proc. 2nd Joint AMI/PASCAL/IM2/M4 Workshop on Multimodal Inter-

action and Related Machine Learning Algorithms (MLMI). Volume LNCS 3869. (2005)

87–100

13. Sanderson, C.: Automatic Person Veriﬁcation Using Speech and Face Information. PhD

thesis, Grifﬁth University, Queensland, Australia (2003)

14. Bonastre, J.F., Wils, F., Meignier, S.: ALIZE, a free toolkit for speaker recognition. In:

Proc. IEEE International Conf. on Acoustics, Speech and Signal Processing ICASP 2005,

Philadelphia, USA (2005) 737–740

15. Richiardi, J., Prodanov, P., Drygajlo, A.: A probabilistic measure of modality reliability in

speaker veriﬁcation. In: Proc. IEEE International Conf. on Acoustics, Speech and Signal

Processing ICASP 2005, Philadelphia, USA (2005) 709–712