A Key Management Method for Cryptographically

Enforced Access Control

Anna Zych

, Milan Petkovi

and Willem Jonker

Twente University

Philips Research

Abstract. Cryptographic enforcement of access control mechanisms relies on

encrypting protected data with the keys stored by authorized users. This approach

poses the problem of the distribution of secret keys. In this paper, a key manage-

ment scheme is presented where each user stores a single key and is capable of

efﬁciently calculating appropriate keys needed to access requested data. The pro-

posed scheme does not require to encrypt the same data (key) multiple times with

the keys of different users or groups of users. It is designed especially for the

purpose of access control. Thanks to that, the space needed for storing public

parameters is signiﬁcantly reduced. Furthermore, the proposed method supports

ﬂexible updates when user’s access rights change.

1 Introduction

Advances in information and communication technologies bring with numerous bene-

ﬁts also concerns with respect to security issues. The data no longer resides on main-

frames physically isolated within an organization, where physical security measures

can be taken to safeguard the data and the system. Modern solutions are evolving to-

wards open, interconnected environment where storage outsourcing and operations on

untrusted servers happen frequently. Open access data storage standards pose new chal-

lenges on security technologies. The old server-centric protection model locks data in a

database server and uses a traditional access control model to permit access to data. To

facilitate current developments, a data-centric protection model is required, where data

is cryptographically protected and allowed to be outsourced or even freely ﬂoat on the

network. In many cases there is a need to replicate the data and send it to the clients.

Examples are distributed databases, grid computing, enterprise rights management sys-

tems and peer-to-peer data management systems in general. Consider for example the

development of Electronic Health Records (EHRs). It aims at increased availability and

sharing of patient records. Records are shared among different healthcare providers, ex-

ternal wellness services and relatives. As the healthcare data is very sensitive, privacy

and security have to be taken care of. Today this often means that access to EHRs is

restricted to a controlled environment of care institutions. This limitation can be over-

come by the more ﬂexible data-centric protection.

In this paper, we address the key management problem of the data-centric protection

model. Namely, when the data is encrypted, the access control policies have to be taken

into account so that control is maintained regarding which users can access what data.

Zych A., Petkovi

c M. and Jonker W. (2007).

A Key Management Method for Cryptographically Enforced Access Control.

In Proceedings of the 5th International Workshop on Security in Information Systems, pages 9-22

DOI: 10.5220/0002432300090022

 SciTePress

The remainder of this paper is organized as follows. Section 2 describes the problem

and surveys the related work. Our key management solution is presented in Section 3.

Section 4 is devoted to the problem of updates of access rights. Section 5 discusses the

advantages of the proposed solution compared to the state-of-the-art. Finally, Section 6

summarizes our contributions.

2 Related Work and Problem Description

A straightforward solution to enforce access control with cryptography is to encrypt the

data with a data key, which is consequently encrypted with the keys of users that should

be able to access this data. The drawback of such approach is that each data key is stored

in multiple copies encrypted with different user keys. The number of copies of a single

data key can reach the number of users (or roles or user groups) in the system. For large

systems that allow ﬁne granularity of access to data, this number can by far exceed the

size of the protected data itself. Another problem is updating encrypted data keys when

the access control policies change. Thus, we search for a method to assign the keys to

the data and the users in a more efﬁcient manner, supporting ﬂexible updates.

There are a number of different deﬁnitions of the key management problem in the

literature. We propose here a generalized problem statement. To the best of our knowl-

edge our deﬁnition covers all the approaches presented in the literature.

Generalized Key Management Problem Let U be the set of users of the system (users

can represent individuals, roles or groups of individuals), and let D be the set of data

records. Any set of users is an access conﬁguration. The set of users allowed to access

data record d ∈ D is an access conﬁguration associated with d, denoted as AC(d). The

access conﬁgurations are partially ordered in a natural way via subset inclusion ⊂ (see

Figure 1c).

The inclusion partial order is used to assign the keys to groups of users. This partial

order satisﬁes more conditions than necessary and therefore wastes opportunities. By

relaxing these, and deﬁning a weaker order relation, we allow partial orders that in turn

allow for more efﬁcient key management.

The necessary conditions for the partial order (P, <) on access conﬁgurations are

as follows. For each user u access conﬁguration {u} belongs to P : ∀

u∈U

{u} ∈ P .

There may be however some additional access conﬁgurations in P , for example AC(d)

for d ∈ D. The order relation < on elements of P satisﬁes (order conditions):

(

⊃ AC

, |AC

| = 1 =⇒ AC

< AC

=⇒ AC

⊃ AC

(1)

This deﬁnition ensures, that if u ∈ AC, then {u} > AC, and requires as few other

order relations as possible. Intuitively, we want to model that the data accessible by the

whole group AC is also accessible by any user u ∈ AC. Examples of orders that satisfy

our deﬁnition are presented in Figure 1.

The task of the key management scheme is to (i) design an efﬁcient

partial order

P satisfying order conditions (1) and (ii) assign to each access conﬁguration AC in P

By efﬁcient we mean with minimal number of conﬁgurations and relations on them, but avoid-

ing multiple copies of data keys.

u1 u2 u3 u4 u5 u6 u7 u8

{ 12} { 34} { 56} { 78}

{ 1234} { 5678}

{ 12345678 }

++++++u7

++++++u8

++++++u6

++++++u5

++++++u4

++++++u3

++--++u2

--++++u1

d6d5d4d3d2d1

ACCESS RI GHTS:

AC(d3)= AC(d4)= {1345678}= {1}«{34}«{5678}

Encrypted data: E(k

,d3) E(k

,d4)

Encrypted keys: E(K

{1}

, k

) E(K

{34}

) E(K

{5678} ,

)

E(K

{1}

, k

) E(K

{34}

) E(K

{5678} ,

)

( a)

u1 u7 u3 u4 u5 u6 u2 u8

AC( d5) = AC( d6 )

= { 2345678}

Dum my AC:

{ 345678}

AC( d1 ) = AC(d2 ) = { 12345678}

AC( d3 ) = AC( d4 )

= { 1345678}

u1 u3 u4 u5 u6 u7 u8 u2

AC( d5 ) = AC( d6 )

= { 2345678}

AC( d3 ) = AC( d4 )

= { 1345678}

Dum my AC:

{ 345678}

AC( d1 ) = AC(d2 ) = { 12345678}

AC(d3)= AC(d4)= {1345678}

Encrypted data: E(k

,d3) E(k

,d4)

Encrypted keys: E(K

{1345678}

, k

)

E(K

{1345678}

)

( b)

( c)

Fig.1. Example of an access table and orders on access conﬁgurations from this table.

on or more secret keys K

, such that based on K

{u}

each user u can obtain K

for every AC < {u}. The data records d ∈ D are encrypted with the data key k

that in turn is encrypted with the keys of groups of users AC

in such a way, that

AC(d) =

. Thus, all the authorized users can access their data. The examples

are shown in Figure 1. In case of broadcast encryption order (Figure 1 a), the data

keys k

and k

are encrypted three times each with the keys of access conﬁgurations

that sum up to AC(d

) = AC(d

). In the two other partial orders in Figure 1 b and

c, AC(d) for each data record d ∈ D is included in the order, thus each data key is

encrypted only once.

Various solutions were proposed to address this problem [1–6]. Practical approaches

designed for cryptographically enforced access control are mostly based on broadcast

encryption [4]. In the basic approach, the users are represented by the leafs and the

access conﬁgurations are represented by the interior nodes of a binary tree. This binary

tree represents the partial order on access conﬁgurations, as shown in Figure 1a. The

user is required to store all the keys on the path from the corresponding leaf to the

root of the tree. She can decrypt all the necessary data with the keys she stores. This

strategy only partially reduces the redundancy described previously, as there are still

multiple copies of data keys. Furthermore, each user stores the number of keys that is

of order of the logarithm of the number of subjects, instead of just a single key as in the

straightforward solution.

A number of improvements of this basic method were proposed. Most of them [5,

6] consider users as stateless receivers, and are referred in the literature as revocation

schemes. The improvements are achieved by introducing more groups, more complex

orderings of these groups, and sophisticated key assignment methods.

Another popular approach constitutes of the key generation schemes [1–3]. Essen-

tially, the partial order is given, and the task of the scheme is to assign the keys to the

elements (access conﬁgurations) of the given order. In the access control settings, that

means that given the key of AC

and some public information one can compute the

key of AC

if and only if AC

< AC

. Support for an arbitrary number of groups

allows the complete elimination of the multiple copies of data keys while, thanks to key

generation mechanism, each user has only one secret key. However, the price to be paid

is the public information that is stored on a public server, used by the users to derive

keys. Especially in the case of access control, it is very important to minimize the public

space, as the size of the partial orders of access conﬁgurations can be exponential in the

number of users.

We discuss the key generation schemes applied to access control (as done in [7])

and compare them with our approach in Section 5.

3 Key Management Solution

In this section we propose an efﬁcient solution for the key management problem stated

above. In Section 3.1, we present an algorithm for constructing the partial order on

access conﬁgurations (AC) satisfying (1). We represent this partial order by an acyclic

and transitively reduced directed graph, where nodes are access conﬁgurations, and arcs

(directed edges) connect comparable elements, from greater to smaller. In the literature,

such a graph is called a Hasse diagram of a partial order. We denote the presence of an

arc from x to y by x −→ y, and a directed path as x ։ y. The constructed graph has

two additional properties referred to as V-conditions:

(

The number of arcs coming into a node is either 2 or 0

For any two nodes, at most one node has arcs into both of them.

(2)

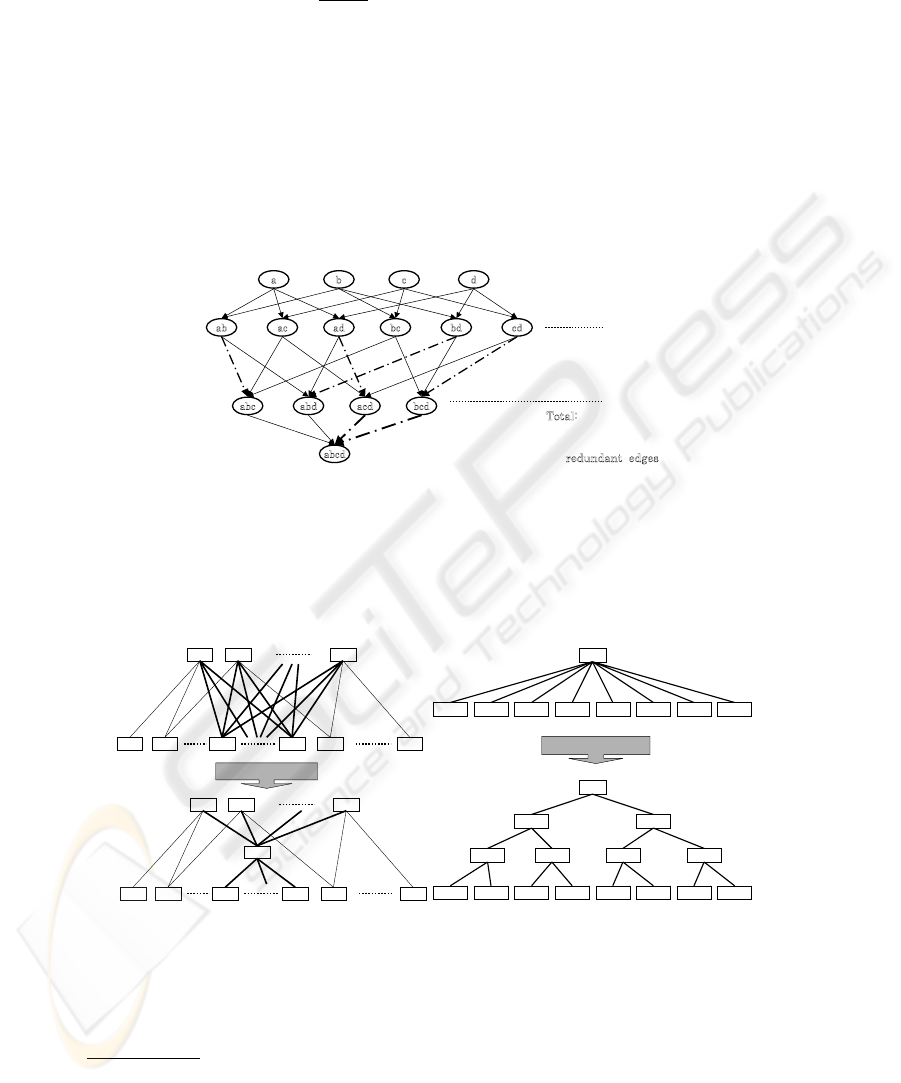
A graph satisfying (2) is a V-graph. Examples of a non V-graph (a) and a V-graph

(2) and representing an order satisfying (1) as access control graph. The V-form of

the graph allows us to apply the Difﬁe-Hellman (DH) based key generation scheme

presented in Section 3.2. The DH scheme assigns public and private keys to the nodes.

Each user receives a single private key and using this key he is able to derive the keys

needed to decrypt the data he has right to access.

3.1 Hierarchy Construction Algorithm

In this section we present the construction of a partial order on access conﬁgurations.

The CreateHierarchy(Access Table ACCESS) algorithm presented in this section takes

as an input an access table (as in Figure 1) and builds an access control graph on access

conﬁgurations (shown in Figure 2 c). Appendices A and B provide the code and the

correctness proof respectively.

The input access table ACCESS is a boolean matrix representing access rights

given to the users. The rows correspond to the users and the columns to the data records.

The value ACCESS[u, d] = true(+) if and only if user u is allowed to access data d.

Each column represents an access conﬁguration of the corresponding data object.

The algorithm consists of the initial phase and the three construction phases de-

scribed below. In the initial phase, the CreateHierarchy algorithm obtains access conﬁg-

urations of all d ∈ D from corresponding columns and stores them in the priority queue

Q, with the priority of AC set to its size |AC|. Smaller conﬁgurations are extracted

earlier. Additionally, all access conﬁgurations containing a single user are inserted to

initially empty graph G.

Let In(x) for x ∈ G denote the set of directed edges (arcs) pointing to x. In the

next phases, the algorithm adds access conﬁgurations and edges to the graph. Some of

these adds may cause previously added edges to be removed. The aim of these transfor-

mations is to obtain a graph satisfying the conditions from Table 1.

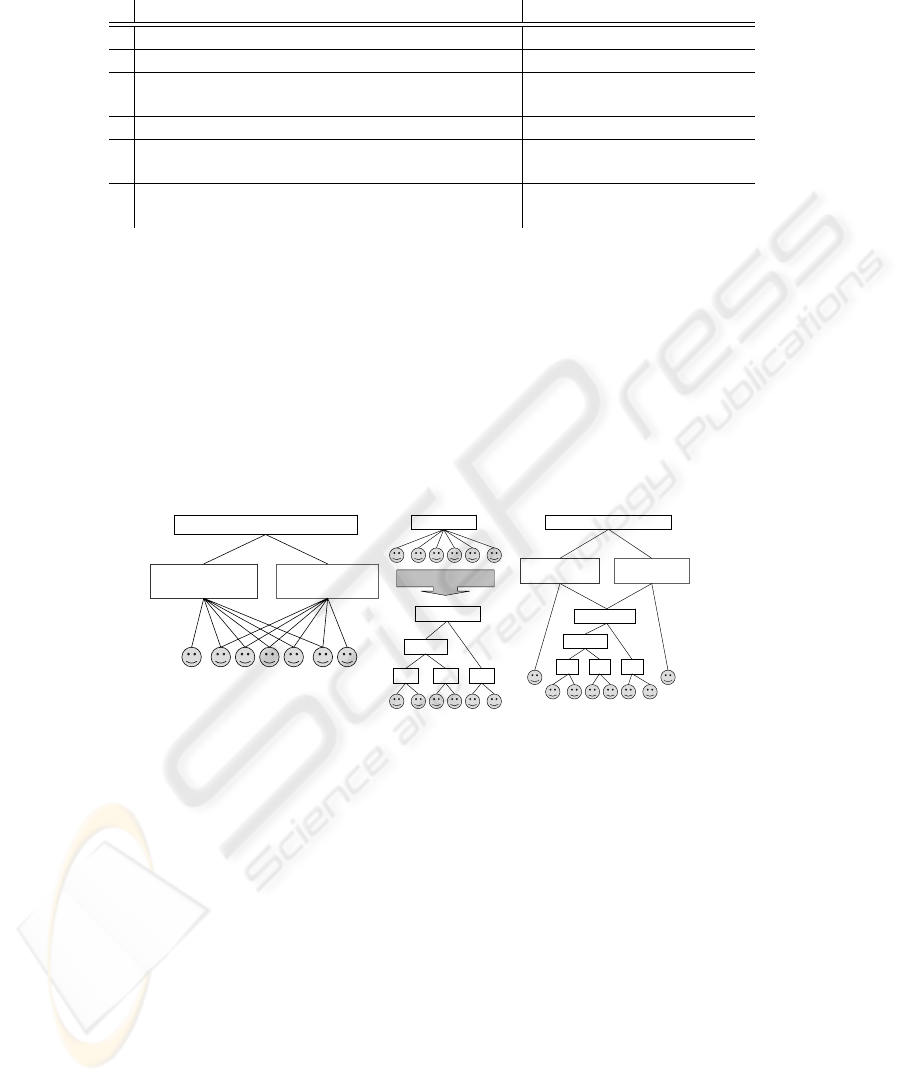
Table 1. Conditions specifying access control graph and their informal description.

Description Condition

a. Access conﬁgurations of all single users belong to G {u} ∈ G for each u ∈ U

a’. Access conﬁgurations of all data records belong to G AC(d) ∈ G for each d ∈ D

b. A user is connected via directed paths with all the u ∈ AC =⇒ {u} ։ AC

conﬁgurations she belongs to (ﬁrst order condition)

b’. Second order condition AC

։ AC

⇒ AC

⊆ AC

c. First V-condition |In(AC)| = 0 or |In(AC)| = 2

for any AC ∈ G

d. Second V-condition |In(AC

) ∩ In(AC

)| ≤ 1

for any AC

, AC

∈ G

In the ﬁrst phase, the algorithm constructs graph G satisfying conditions (a − b

′

Queue Q stores the conﬁgurations that still need to be added to G. As before smaller

conﬁgurations are extracted earlier. For each extracted conﬁguration AC the algorithm:

1. inserts AC to graph G

2. ﬁnds in G the minimal set cover of AC, that is a minimal set of conﬁgurations AC

already in G, such that AC =

3. inserts an edge AC

−→ AC for each AC

from the found cover

until Q is empty (see Appendix A procedure InsertCoveredMin(AC)). Trivially, (a −b

′

)

are satisﬁed after completing this phase. For the example access table from Figure 1,

the graph obtained after this phase is shown in Figure 2a.

u1 u7 u3 u4 u5 u6 u2

AC( d5) = AC( d6)

= { 2345678}

AC( d3) = AC( d4)

= { 1345678}

AC( d1) = AC( d2) = { 12345678}

( a)

{ 12} { 34} { 56}

{ 123 4}

{ 123 456}

CreateTree

( b)

u3 u4 u5 u6 u7 u8

AC(d5) = AC( d6)

= { 23 4567 8}

AC(d3) = AC( d4)

= { 13 4567 8}

{ 345 678}

AC(d1) = AC(d2) = { 123 4567 8}

{ 34} { 56}

{ 345 6}

{ 78}

u1 u2

( c)

Fig.2. (a) graph obtained after the ﬁrst phase applied to table in Figure 1; (b) transformation

CreateTree applied in the third phase; (c) the ﬁnal result of the algorithm applied to the table in

Figure 1.

In the second phase, the algorithm transforms the graph to preserve conditions

(a − b

′

), and reduce the number of incoming edges to at most two per node. Queue

Q stores conﬁgurations that need to be processed by the algorithm, that is those with

more than two incoming edges. The algorithm extracts the conﬁgurations with a greater

number of incoming edges ﬁrst. For each extracted conﬁguration AC, the algorithm

looks at conﬁgurations AC

′

in Q, and considers their intersection AC ∩ AC

′

with AC.

For each AC

′

, AC ∩ AC

′

is a potential new conﬁguration to be added to graph G.

Note, that if X ⊂ AC ∩ AC

′

⊂ AC, then adding conﬁguration AC ∩ AC

′

and edges

X → AC ∩ AC

′

, AC ∩ AC

′

→ AC, makes edge X → AC unnecessary by transitiv-

ity. The algorithm chooses AC

′

in a way, that adding conﬁguration AC ∩ AC

′

allows

to reduce the maximal number of edges coming into AC. It repeats this step, until no

more edges in In(AC) can be reduced in this manner. During these transformations,

the numbers of incoming edges of conﬁgurations AC

′

are reduced as well. The con-

ﬁgurations, whose incoming edges were reduced to at most two are removed from Q.

After completing the loop described above, the graph for our running example is shown

in Figure 1c. Condition (d) is satisﬁed trivially after the termination of the second phase

(see Appendix B).

In the third phase, if after the second phase there are AC in G such that |In(AC)| >

2, then the algorithm reduces |In(AC)| by substituting In(AC) with a binary tree

rooted in AC (see Appendix A procedure CreateTree(AC)), as shown in Figure 2b. The

leafs are the nodes connected to AC with arcs In(AC). After this step, |In(AC)| = 2

and AC can be removed from Q. The algorithm continues the third phase until Q is

empty.

Note, that |In(AC)| = 1 cannot hold for any AC. At the end of the third phase, all

(a − d) are satisﬁed (see Appendix B), and the algorithm terminates. The ﬁnal result of

the algorithm for the running example is shown in Figure 2c.

3.2 Difﬁe-Hellman based Key Generation Scheme

In this section, we describe a key generation scheme for an access control graph re-

turned by algorithm CreateHierarchy(Access Table ACCESS), which was presented in

Section 3.1. The security of the scheme follows directly from the security of the DH

key exchange protocol.

Key Assignment. Let LeftParent(AC) and RightParent(AC) be the nodes of In(AC).

We assign private and public keys to the nodes of G, according to the Difﬁe Hellman

key exchange protocol. If In(AC) is empty then the secret key of AC is a randomly

chosen number. Otherwise the secret key of AC is a shared key obtained by applying

Difﬁe-Hellman protocol on the private and public keys of LeftParent(AC) and RightPar-

ent(AC), treating them as the key exchanging parties. The public key of AC is obtained

from its private key according to the Difﬁe-Hellman protocol. Thus, each AC is labeled

with its private key S

and its public key P

as follows:

(

= g

Lef tP arent(AC)

·S

RightP arent(AC)

mod p

:= g

mod p

(3)

Key Derivation. To derive the key of a descendant node, a node needs its own secret

key, as well as the public keys of the “other” parents in the path to the target node.

It recursively derives child keys along the path to the target, by calculating S

child

other parent

)

parent

4 Updates

This section shows how to efﬁciently deal with the updates of the access control poli-

cies. The updates to the policies can be categorized according the amount of change

they cause in the database. Each category requires different steps to be taken to reen-

crypt the necessary data. The table in Figure 3 presents four categories covering all

possible scenarios of access control policy update. According to the nature of the in-

troduced update, we apply a combination of three basic steps as presented in the table.

Below we describe these basic steps and their effects on the database.

An existing object

hanges the assigned

ccess configuration into

nother existing one

Steps: Rekey DO.

A new access

onfiguration is assigned

o an existing data object

Steps: Insert AC,

Rekey DO.

Existing

Steps: Rekeying Data

bject DO

A new data object is

ssigned to an existing

ccess configuration

Steps: Add DO.

A new data object is

ssigned a new access

onfiguration

Steps: Insert AC,

dd DO.

New

Steps: Adding Data

bject DO

Existing

Steps: Not needed

New

Steps: Inserting Access

onfiguration AC

Access

onfiguration

Data

Object

A,B,C,D,E,F

A,C,D,E,F B,C,D,E,F

C,D,E,F

C D E F

A B

C,D E,F

B,E,F,G

A,B,C,D,E,F

A,C,D,E,F B,C,D,E,F

C,D,E,F

C D E F

C,D E,F

B,E,F,G

A,B,C,D,E,F

A,C,D,E,F B,C,D,E,F

C,D,E,F

C D E F

C,D E,F

B,E,F,G

B,G

Access configuration

joins the hierarchy

(1) (2)

Fig.3. Update scenarios and example.

The Insert Access Conﬁguration (Insert AC) step is needed when new access con-

trol policies imply a new access conﬁguration AC

new

, which is not an element of the

current hierarchy (represented by an access control graph). This is the only step, in

which the hierarchy must be updated. We proceed as follows. The new node is cre-

ated in the hierarchy for AC

new

. It is not assigned any children. If it were, then the set

{X ∈ G : ∃

Z∈G

new

։ Z and X ։ X} must be assigned new keys. This could

require the re-encryption of the whole hierarchy. Thus, to insert AC

new

, we apply the

operations G.InsertCoverM in(AC

new

) and G.CreateT ree(AC

new

) (see Section

3.1). After these two steps conditions [a-d] from Section Table 1 remain satisﬁed and

we can generate new keys for new nodes using the DH scheme. No rekeying is required

whatsoever. Frequent updates of the hierarchy inﬂuence the performance and public

space. Therefore after a certain number of updates the whole hierarchy is rebuilt and

rekeyed. If the access conﬁguration in the hierarchy does not correspond to any data

object, it is not removed until the hierarchy is rebuilt, and remains as a virtual node.

Applying updates to an example hierarchy is shown in Figure 3.

The Add Data Object (Add DO) step is required when a new data object is assigned

an existing access conﬁguration. In this case, a new secret key for the new data object

is created, the object is encrypted with the new key, and the new key is encrypted with

the key of the (existing) access conﬁguration assigned to the object.

The Rekey Data Object (Rekey DO) step is performed, when an access conﬁgura-

tion AC

old

assigned before to a data object d ∈ D is changed into another existing

access conﬁguration AC

new

. Assume K(d) is the data encryption key assigned to d,

K(AC

new

) and K(AC

old

) are the key encryption keys corresponding to these access

conﬁgurations. There are two possible cases:

1. AC

old

⊂ AC

new

: in this case the users gain access rights and K(d) is re-encrypted

with K(AC

new

)

2. otherwise: in this case the users loose rights and K(d) must be changed into K

new

(d),

d is re-encrypted with K

new

(d), K

new

(d) is encrypted with K(AC

new

) and stored.

5 Discussion

In this section, we compare our scheme to the schemes described in Section 2. Com-

pared to broadcast encryption methods, the solution we propose eliminates the need for

multiple copies of data keys and reduces to a single key the storage required per user.

Therefore, we focus in this section on the comparison of our scheme with the key gen-

eration schemes. For the sake of a clear comparison we divide them into two groups:

PKC (Public Key Cryptography) based schemes and SKC (Symmetric Key Cryptogra-

phy) based schemes.

Let n be the size of a partial order to which a PKC scheme is applied. The PKC

based solutions are essentially extensions of two basic approaches. The ﬁrst approach

requires storing large public keys proportional to the product of ﬁrst n primes: p

·· · ··p

[1,8,9]. The upper bound for the product of n primes is (n log n)

, so the size in bits

required to store it is log(n log n)

= n log(n log n). Each key derivation step requires

a single operation, but computation on numbers of that size implies the time needed for

the key derivation proportional to n. In the second approach, the number of modular

exponentiations needed for computing the private keys is proportional to n [2,10, 11].

This is applicable for reasonably small partial orders, for instance hierarchies inside

a company or an institute. However in our settings, assuming that N is the number of

users, the number n of possible access conﬁgurations can reach 2

. Therefore the direct

application of these schemes for partial order on access conﬁgurations results in a key

derivation time that is exponential in N .

In the scheme we propose, all the private and public keys are bounded from above

by a large prime number p. To ensure that the keys are unique, p must be of order n

for

some constant α. Therefore the size of a public key is bounded from above by α log n. It

is in the worst case proportional to N . The key derivation time in the proposed scheme

is proportional to the height of the partial order. Since the height of a partial order on

access conﬁgurations cannot exceed N, the derivation time is bounded from above by

N. An additional advantage of our scheme is the support for ﬂexible updates, which are

poorly supported in the PKC based schemes.

The SKC based schemes [2, 12, 13, 3] are more efﬁcient, however some successful

attacks against them have been proposed [14]. Furthermore, we argue below that in

terms of storage space our scheme is more efﬁcient than any of these schemes applied

directly to an inclusion partial order on access conﬁgurations.

Essentially, the SKC based schemes assign the private keys to the nodes and public

keys to the edges of the given partial order. When the nodes are access conﬁgurations,

this order is naturally given by set inclusion. It is represented by a directed graph with n

nodes (access conﬁgurations) and e edges. An SKC based scheme assigns O(n) private

and O(e) public keys. As emphasized in the problem statement given in Section 2,

inclusion order gives many redundant edges, which in turn give many redundant public

parameters. Intuitively, our partial order construction aims at minimizing the number of

edges.

A perceptive reader spots immediately that our scheme assigns both private and

public keys to the nodes of the partial order we construct. However, for each node AC

except for N singletons {u} we have |In(AC)| = 2 (V -condition). Therefore, the

number of nodes is equal to

|edges|

+ N, and this is the number of public keys issued

by our scheme

This does not complete the analysis, because the number of edges in the order we

construct is different than in the inclusion order. Let n and e be the number of nodes

and edges in the inclusion order given on access conﬁgurations {u}

u∈U

and AC(d)

d∈D

Let n

′

and e

′

be the number of nodes and edges in our construction after the t th phase

of the algorithm. After the ﬁrst phase, the following conditions are satisﬁed: e

′

≤ e

and n

′

= n. This is due to the weaker order conditions deﬁned in Section 2. When

constructing the order, we insert only necessary edges that connect users with access

conﬁgurations they belong to, thus for many inclusions AC

⊂ AC

there is no relation

(edge) in the constructed order. An example is shown in Figure 4.

dcba

cdbdbcadacab

bcdacdabdabc

abcd

redundant edges

i-1 th level

i th level

 

x

i 2

redundant

edges

otal:

redundant edges

 

x

Fig.4. Full access control hierarchy.

After the second phase, the number of edges decreases even more: e

′

≤ e

′

. Each

inserted dummy access conﬁguration D decreases |In(AC

)| by α ≥ 2 conﬁgurations.

The precise number of edges after inserting D changes from e

′

to e

′

−(α−1)·|In(D)|+

α as shown in Figure 5a.

AC’

m- a

AC’

m- a_ 1

AC’

m- a

AC’

m- a_ 1

AC’

( a)

I n( AC)

CreateTree( AC)

I n( AC)

( b)

Fig.5. Insertion of a dummy access conﬁguration D and tree transformation.

After the third phase, e

′

≤ 2e

′

− 1, so the number of edges at most doubles. This is

due to the transformations made by function CreateT ree(AC), which transforms AC

|X| denotes the number of elements of set X

with In(AC) into a binary tree with AC as a root and In(AC) as leaves (see Figure 5

b). Each call of CreateT ree(AC) adds |In(AC)| − 1 edges.

Thus, in the end we have e ≥ e

′

≥ e

′

≥

′

and n

′

+ N is the number of

public parameters in our scheme. This in practice means that in the worst case, when

all the reductions of edges do not bring any result, we use at most (e + N) public

parameters, whereas SKC based schemes use at least e. However, when dealing with

a few or many intersecting access conﬁgurations we expect an improvement, as shown

in the ﬁgures. The number of private parameters remains the same for both SKC based

schemes and our scheme and is equal to n = n

′

, since we do not have to store the

private keys for dummy access conﬁgurations. Concluding this comparison, it is worth

mentioning that the security of our scheme is guaranteed by the security of well-known

DH key-exchange protocol.

6 Conclusions

In this paper, we proposed an efﬁcient method to design a partial order on access con-

ﬁgurations. We provided a scheme to assign and derive secret keys for the proposed

partial order.

Compared to broadcast encryption methods, our solution eliminates the need for

multiple copies of data keys and reduces to a single key the storage required per user.

This improvement is achieved by applying the proposed key generation scheme. Com-

pared to key generation schemes adapted for access control purposes, our solution re-

duces the required size of public information. This is achieved thanks to the special

properties of the hierarchy we propose, designed especially for the access control pur-

pose. To the best of our knowledge, and as reported in [15], nobody has yet proposed

a key generation solution that takes advantage of constructing the hierarchy especially

for the access control settings.

Finally, since access control systems are very dynamic, the issue of changing ac-

cess rights cannot be neglected. Our solution supports ﬂexible updates of access rights

granted to the users.

References

1. Akl, S.G., Taylor, P.D.: Cryptographic solution to a problem of access control in a hierarchy.

ACM Trans. Comput. Syst. 1 (1983) 239–248

2. Harn, L., Lin, H.Y.: A cryptographic key generation scheme for multilevel data security.

Comput. Secur. 9 (1990) 539–546

3. Lin, C.H.: Dynamic key management schemes for access control in a hierarchy. Computer

Communications 20 (15 December 1997) 1381–1385(5)

4. Fiat, A., Naor, M.: Broadcast encryption. In: CRYPTO ’93: Proceedings of the 13th an-

nual international cryptology conference on Advances in cryptology, New York, NY, USA,

Springer-Verlag New York, Inc. (1994) 480–491

5. Naor, D., Naor, M., Lotspiech, J.B.: Revocation and tracing schemes for stateless receivers.

In: CRYPTO ’01: Proceedings of the 21st Annual International Cryptology Conference on

Advances in Cryptology, London, UK, Springer-Verlag (2001) 41–62

6. Asano, T.: A revocation scheme with minimal storage at receivers. In: ASIACRYPT ’02:

Proceedings of the 8th International Conference on the Theory and Application of Cryptol-

ogy and Information Security, London, UK, Springer-Verlag (2002) 433–450

7. Bertino, E., Carminati, B., Ferrari, E.: A temporal key management scheme for secure broad-

casting of xml documents. In: CCS ’02: Proceedings of the 9th ACM conference on Com-

puter and communications security, New York, NY, USA, ACM Press (2002) 31–40

8. TS Chen, Y.C.: Hierarchical access control based on chinese remainder theorem and sym-

metric algorithm. Computers & Security 21 (2002) 565–570

9. Kuo, F.H., Shen, V.R.L., Chen, T.S., Lai, F.: Cryptographic key assignment scheme for

dynamic access control in a user hierarchy. Volume 146., Dept. of Electr. Eng., Nat. Taiwan

Univ., Taipei, IEE (September 1999) 235 – 240

10. Hwang, M.S., Yang, W.P.: Controlling access in large partially ordered hierarchies using

cryptographic keys. J. Syst. Softw. 67 (2003) 99–107

11. Lin, I.C., Hwang, M.S., Chang, C.C.: A new key assignment scheme for enforcing compli-

cated access control policies in hierarchy. Future Gener. Comput. Syst. 19 (2003) 457–462

12. Chien, H-Y; Jan, J.K.: New hierarchical assignment without public key cryptography. Com-

puters & Security 22 (2003) 523–526

13. Lin, C.H.: Hierarchical key assignment without public-key cryptography. Computers &

Security 20 (2001) 612–619

14. Lee, N.Y., Hwang, T.: Comments on dynamic key management schemes for access control

in a hierarchy’. Computer Communications 22 (1999) 87–89

15. Crampton, J., Martin, K., Wild, P.: On key assignment for hierarchical access control. In:

CSFW ’06: Proceedings of the 19th IEEE Workshop on Computer Security Foundations,

Washington, DC, USA, IEEE Computer Society (2006) 98–111

A Appendix: The Algorithm

The output of the CreateHierarchy(Access Table ACCESS) algorithm is the directed

graph G = (V, E(V )) in a V-form, where the node set V ⊇ {AC(d)|d ∈ D}. The

algorithm uses an abstract data structure Digraph G to represent the order on access

conﬁgurations it constructs. The standard available operations are: New(), Cover(Node

A), InsertNode(Node A), InsertEdge(Node A, Node B), RemoveNode(Node A) and Re-

moveEdge(Node A, Node B). We assume that the graph does not allow duplicate nodes

(if the node to be inserted already exists, than the insertion procedure terminates). Sim-

ilarly, no multiple arcs are allowed between two nodes. The algorithm CreateHierar-

chy(Access Table ACCESS) uses the priority queue Q. A priority queue is an abstract

data type to efﬁciently support ﬁnding the item with the highest priority across a series

of operations. The basic operations are: New(), Insert(Item, Priority), ExtractMax(),

ExtractMin(), FindMax(), FindMin() and Remove(Item). The items of Q are the access

conﬁgurations. The algorithm calls two additional procedures: InsertCoverMin(Node

AC) and CreateTree(Node AC), which are presented in Section A.1. The number of el-

ements in data structure X is denoted as #X. For data structures X and Y we denote

their set difference (the elements in X but not in Y ) as X − Y , and their intersection as

X ∗ Y .

A.1 Subprocedures Codes

algorithm InsertCoveredMin(Node AC)

begin

(1) G.InsertNode(AC);

(2) Node X:=AC;

(3) while (#X > 0) do

begin

(4) Node Y := maximal Z in G, s.t. X contains Z;

(5) G.InsertEdge(Y,X);

(6) X:=X - Y;

end

end.

algorithm CreateTree(Node AC)

begin

(1) pos:=0;

(2) for each (X in G s.t. X ->> AC) do

begin

Q.Insert(X,pos++);

(3) while (#Q > 2) do

begin

(4) AC_1:=Q.ExtractMin(); AC_2:=Q.ExtractMin();

(5) Node Y:=AC_1 + AC_2; (6) G.InsertNode(Y);

(7) G.InsertEdge(AC_1,Y); G.InsertEdge(AC_2,Y);

(8) G.RemoveEdge(AC_1,AC); G.RemoveEdge(AC_2,AC);

(9) G.InsertEdge(Y,AC); (10) Q.Insert(Y,position++);

end

end.

A.2 The Main Code

algorithm CreateHierarchy(Access Table ACCESS)

begin

(1) Digraph G := New(); PriorityQueue Q := New();

(2) for each (u in U) do G.InsertNode({u});

(3) for each (d in D) do Q.Insert(AC(d),#AC(d));

(4) while (Q.size() > 0) do

begin

(5) AC:=Q.ExtractMin();

(6) G.InsertCoveredMin(AC);

end

(7) for each (AC in G s.t. #In(AC) > 2) do Q.Insert(AC,#In(AC));

(8) repeat

(9) Node AC:=Q.FindMax(); MAX_CUT := empty set;

(10) for each (AC_k in Q) do

begin

(11) CUT:=AC

AC_k;

(12) if ( #{X in G s.t. X ->> AC, CUT contains X }

> #{ X in G s.t. X ->> AC, MAX_CUT contains X}

AND

there are X,Y in G

s.t. X != Y, X,Y ->> AC, CUT contains X

AND

there are X,Y in G

s.t. X != Y, X,Y ->> AC_k, CUT contains X

(13) then MAX_CUT := CUT;

end // for each

(14) if (MAX_CUT not empty) (15) then // if MAX_CUT found

begin

(16) G.InsertCoveredMin(MAX_CUT);

(17) for each (X in Q) do

begin

(18) if (X contains strictly MAX_CUT

AND

there are Y,Z in G s.t. Y != Z,

Y,Z ->> X, MAX_CUT contains X

(19) then

begin

(20) G.InsertEdge(MAX_CUT,X);

(21) for each (Y in G s.t. Y ->> X, MAX_CUT contains Y) do

G.RemoveEdge(Y,X);

(22) if (#In(X) <= 2) then Q.Remove(X) ,

end // if

end //for each

(23) if (#In(MAX_CUT) > 2)

(24) then Q.Insert(MAX_CUT,#In(MAX_CUT));

end // if

(25) else G.CreateTree(AC); Q.Remove(AC);

(26) until Q is empty; // repeat

end.

B Appendix: Correctness Proof

Lemma 1 After the termination of the algorithm CreateHierarchy, the output graph

G = (V, E(V )) satisﬁes the following ﬁve conditions:

(a) ∀

u∈U

{u} ∈ V

(a’) ∀

d∈D

AC(d) ∈ V

(b) u ∈ AC ⇒ {u} ։ AC

(b’) AC

։ AC

⇒ AC

⊆ AC

AC∈V

|In(AC)| = 0 or |In(AC)| = 2

(d) ∀

,AC

∈V

|{AC ∈ V : AC −→ AC

, AC −→ AC

}| ≤ 1

Proof. In the ﬁrst phase (1-6), the algorithm constructs the hierarchy, which satisﬁes

(a), (a’), (b) and (b’). Since the arcs are added only between such two conﬁgurations,

that one contains the other, (b’) remains trivially satisﬁed until the termination. After

addition of singletons (2) G satisﬁes (a), and after addition of existing access conﬁgu-

rations (3-6), G satisﬁes (a’) as well. Both (a) and (a’) are not affected by the algorithm

anymore and remain satisﬁed until termination. After line (2) G satisﬁes (b) trivially

because V is the set of singletons. (b) remains satisﬁed after each step of the main algo-

rithm until line (21), because the procedures InsertCoveredMin and CreateTree preserve

(b), and only in line (21) the edges are removed so (b) has a chance to be affected.

In the second phase, from line (7), additional access conﬁgurations are inserted to

reduce the number of edges and satisfy the condition (c). Beginning at line (7) until the

termination, Q stores the nodes AC ∈ V for which |In(AC)| > 2 and thus they still

need to be processed. The priorities of the items on Q determine the order of process-

ing the nodes of G. The priority of an item AC is |In(AC)|. The nodes with larger

In(AC) are processed ﬁrst. The main loop REPEAT (8-26) is terminated when Q is

empty, so all the nodes have at most two incoming edges. In (9) node AC, with the

maximal number of incoming edges, is extracted from Q to reduce |In(AC)|. After

current iteration of the main loop, the size |In(AC)| is reduced, and therefore each it-

eration reduces the number of incoming edges of a node, with the maximal number of

incoming edges in G. Thus, at some point the maximal number of incoming edges in G

must reach 2. This guarantees that the loop terminates. In lines (10-13), the algorithm

searches for the dummy access conﬁguration M AX

CU T , which insertion reduces

|In(AC)| maximally, under the assumption that it also reduces |In(AC

)| for some

other access conﬁguration AC

still stored on Q. If (14) MAX CU T was found, then

(15) it is inserted into G (16), and for each node X on Q (17) the algorithm checks

(18) whether |In(X)| can be reduced using M AX

CU T . If the condition from line

(18) is satisﬁed, then MAX CU T −→ X is added to |In(X)| (20), but then based

on (18) at least two edges in In(X) are removed in (21), and therefore |In(X)| de-

creases at least by one. AC satisﬁes (18), thus one of the iterations of loop for each

(17-24) reduces In(AC) for a node AC with the maximal number of incoming edges

in G. In(MAX

CU T ) does not increase back the maximal number of incoming edges

in G, because |In(M AX CUT )| < |In(AC)|. Based on (18), (b) is preserved after

each execution of line (21). In (23) the algorithm enqueues MAX

CU T if it needs to

be processed. If (25) M AX CUT was not found, then |In(AC)| is reduced to 2 by

inserting to G a binary tree rooted in AC with conﬁgurations X : X −→ AC as leaves.

The result of the algorithm is the V-graph satisfying (a-d).