
Conceptual Vectors - A Complementary Tool to Lexical
Networks
Didier Schwab
1
, Lim Lian Tze
1
and Mathieu Lafourcade
2
1
Computer-Aided Translation Unit (UTMK) School of Computer Sciences
Universiti Sains Malaysia, Penang, Malaysia
2
Universit
´
e Montpellier II-LIRMM, Montpellier, France
Abstract. There is currently much research in natural language processing fo-
cusing on lexical networks. Most of them, in particular the most famous, Word-
Net, lack syntagmatic information and especially thematic information (”Tennis
Problem”). This article describes conceptual vectors that allows the representa-
tion of ideas in any textual segment and offers a continuous vision of related
thematics, based on the distances between these thematics. We show the charac-
teristics of conceptual vectors and explain how they complement lexico-semantic
networks. We illustrate this purpose by adding conceptual vectors to WordNet by
emergence.
1 Introduction
Originally resulting from Ross Quillian’s work on psycholinguistics [1], lexical net-
works are today object of many researches in Natural Language Processing. They are
employed in many tasks (lexical disambiguation [2]) or field applications (machine
translation with multilingual networks like Papillon [3] or [4], information retrieval or
text classification [5]). Most of these networks and specifically the most famous, Word-
Net [6], miss syntagmatic information and, in particular, information concerning the
domain usage of terms or at least thematicaly related terms. There is thus no direct rela-
tion between terms like ֒teacher֓-֒student֓ or ֒boat֓-֒port֓. This phenomenon is called the
”tennis problem” [[6], p. 10] because it has been noticed that it was necessary to seek
֒ball֓, ֒racket֓ and, ֒court֓ at various places of the hierarchy.
For several years, TAL team (Natural Language Processing team) from LIRMM
(Montpellier Laboratory of Computer Science, Robotics, and Microelectronics) works
on a formalization of the projection of the linguistic concept of semantic field in a vector
space, the conceptual vectors. They allow to represent ideas contained in an unspecified
textual segment and allow to obtain a continuous vision of thematic used thanks to the
calculable distances between them.
In this article, we present the conceptual vectors and especially the version built by
emergence. We show their characteristics and why they are complementary to lexico-
semantic networks. We illustrate our purpose by an experiment done at UTMK (Computer-
Schwab D., Lian Tze L. and Lafourcade M. (2007).
Conceptual Vectors - A Complementary Tool to Lexical Networks.
In Proceedings of the 4th International Workshop on Natural Language Processing and Cognitive Science, pages 139-148
DOI: 10.5220/0002434801390148
Copyright
c
SciTePress

Aided Translation Unit), Universiti Sains Malaysia, Penang which consisted in enrich-
ing the WordNet data by conceptual vectors built by emergence.
2 Lexico-semantic Networks: Example of WordNet
2.1 Principle
WordNet is a lexical database for English developed under the direction of George
Armitage Miller by the Cognitive Science Laboratory of the university of Princeton
(New Jersey, USA). It aims to be consistant with the access to the human mental lexicon.
WordNet is organized in sets of synonyms called synsets. To each synset corre-
sponds a concept. Terms meaning is described in WordNet by three means :
– their definition
– the synset to which the meaning is attached.
– the lexical relations which link synsets. There are, among others, hyperonymy, la
meronymy and antonymy.
WordNet 2.0 contains 152059 terms what constitutes a relatively broad cover of the
English language. In first versions of Wordnet, the lexical relations connect only items
in the same part of speech. There is thus one hierarchy for nouns, one for adjectives,
one for verbs and finally one for the adverbs.
2.2 Weakness of Wordnet
In [7], authors of WordNet (we were at version 1.6) record six weaknesses in the their
network constitution:
1. the lack of connections between noun and verb hierarchies;
2. limited number of connections between topicallyrelated words;
3. the lack of morphological relations;
4. the absence of thematic relations/selectional restrictions;
5. some concepts (word senses) and relations are missing;
6. since glosses were written manually, sometimes there is a lack of uniformity and
consistency in the definitions.
If items 3, 5 and 6 don’t interest us in this article, we will show the conceptual vec-
tors contribution to the resolution of the others, all three constitue the tennis problem.
2.3 Previous Work to Solve the Problem
In this article, we will be interested only in Wordnet version 2.1 which was the last
available when we carried out our experiments. A new version (3.0) was relised in De-
cember 2006 but it does not seem to have some improvements compared to the previous
version for what interests us here.
Since version 2, relations as derivationally related form makes it possible to link
adjectives to verbs or adjectives to names. In the same way, an usage domain can be
140

addressed to synsets. However, the number of these data still seem too restricted to
be sufficiently relevant. Typical relations as ֒teacher֓-֒student֓ ֒boat֓-֒port֓ or ֒doctor֓-
֒hospital֓, often essential to a task of lexical disambiguation, are not still present and
the restricted number of thematic indications like domain does not make it possible to
compensate this defect. Several solutions were proposed to solve whole or part of this
problem.
With Extended WordNet, [7] proposes to disambiguate definitions of WordNet as a
semi-automatic way. The idea is for each definition to annot each word with the number
of the meaning used. One can then compare two synsets and evaluate their similarity.
We will see that we use this information to manufacture the conceptual vectors of this
experiment.
Others also add information to the synsets. Thus, [8] add lexical signatures resulting
from tagged corpora or Web.
On the other hand, others rather seek to increase the number of arc existing. [9], for
example, combines different metrics to create links between synsets from their defini-
tions and from a thesaurus. [10] use a coocurrences network to extract typical relations
like those presented in the previous section.
We can see that all these proposals have in common to belong in particular to the
discrete field. Our is to introduce a continuous representation of the ideas contained into
the network, conceptual vectors.
3 Conceptual Vectors
3.1 Principle and Thematic Distance
We represent thematic aspects of textual segments (documents, paragraph, phrases, etc)
by conceptual vectors. Vectors have long been used in information retrieval [11] and
for meaning representation in the LSI model [12] from latent semantic analysis (LSA)
studies in psycholinguistics. In computational linguistics, [13] proposed a formalism for
the projection of the linguistic notion of semantic field in a vectorial space, from which
our model is inspired. From a set of elementary concepts, it is possible to build vectors
(conceptual vectors) and to associate them to any linguistic object. This vector approach
is based on known mathematical properties. It is thus possible to apply well founded
formal manipulations associated to reasonable linguistic interpretations. Concepts are
defined from a thesaurus (in our prototype applied to French, we used Larousse the-
saurus [14] where 873 concepts are identified) to compare with the thousand defined
in Roget thesaurus [15]). Let
C be a finite set of n concepts, a conceptual vector V is
a linear combinaison of elements c
i
of
C . For a meaning A, a vector V(A) is the de-
scription (in extension) of activations of all concepts of
C . For example, the different
meanings of ֒door֓ could be projected on the following concepts (the CONCEPT⌈intensity⌋
are ordered by decreasing values): V(֒door֓) = (OPENING⌈0.8⌋, BARRIER⌈0.7⌋, LIMIT⌈0.65⌋,
PROXIMITY⌈0.6⌋, EXTERIOR⌈0.4⌋, INTERIOR⌈0.39⌋, . ..
3.2 Operations on Vectors
Angular Distance. Comparison between conceptual vectors is done using angular dis-
tance. For two conceptual vectors A and B,
141

Sim(X,Y) = cos(
d
X,Y) =
X·Y
kXk×kYk
D
A
(A,B) = arccos(Sim(A, B))
(1)
Intuitively, this function constitutes an evaluation of the thematic proximity and
measures the angle between the two vectors. We would generally consider that, for
a distance D
A
(A,B):
– if ≤
π
4
(45
◦
), A and B are thematically close and share many concepts;
– if D
A
(A,B) ≥
π
4
, the thematic proximity between A and B would be considered as
loose;
– around
π
2
, they have no relation.
D
A
is a real distance function. It verifies the properties of reflexivity, symmetry and
triangular inequality. We have, for example, the following angles (values are in radian
and degrees).
D
A
(V(֒tit֓), V(֒tit֓))=0 (0
◦
)
D
A
(V(֒tit֓), V(֒bird֓))=0.55 (31
◦
)
D
A
(V(֒tit֓), V(֒sparrow֓))=0.35 (20
◦
)
D
A
(V(֒tit֓), V(֒train֓))=1.28 (73
◦
)
D
A
(V(֒tit֓), V(֒insect֓))=0.57 (32
◦
)
The first one has a straightforward interpretation, as a ֒tit֓ cannot be closer to any-
thing else than itself. The second and the third are not very surprising since a ֒tit֓ is a
kind of ֒sparrow֓ which is a kind of ֒bird֓. A ֒tit֓ has not much in common with a ֒train֓,
which explains the large angle between them. One may wonder why ֒tit֓ and ֒insect֓,
are rather close with only 32
◦
between them. If we scrutinise the definition of ֒tit֓ from
which its vector is computed (Insectivourous passerine bird with colorful feather.) per-
haps the interpretation of these values would seem clearer. In effect, the thematic is by
no way an ontological distance.
3.3 Neighbourhood: A Continuous Vision of Thematic Aspects
Principle. The thematic neighbourhood function
V is the function which returns the n
closest LEXICAL OBJECTS
3
to a lexical object x according to the angular distance:
σ×IN → σ
k
:
X, k →E = V (D
A
,X,k)
(2)
where σ the set of LEXICAL OBJECTS. The function
V is defined by :
V (D
A
,Z,k)
= k
∀X ∈
V (D
A
,Z,k), ∀Y /∈ V (D
A
,Z,k),
D
A
(X, Z) ≤ D
A
(Y, Z)
(3)
Thematic neighborhood function can be used for learning to check the overall rele-
vance of the semantic base or to find the more appropriate word to use for a statement.
3
We call LEXICAL OBJECT any object in the lexicon which meaning can be described. For
WordNet, they are entries (called in this article lexical items) and synset.
142

Thus, they give new tools to access words through a proximity notion to those described
in [16] and issued from psycholinguistic considerations like form, part of speech, nav-
igation in a huge associative network. They allow to navigate in a continuous way and
not in a discrete way as commonly done in semantic networks.
Examples. For example, we can have :
V (D
A
, ֒life֓, 7)=(֒life֓ 0.4) (֒to born֓ 0.449) (֒alive֓ 0.467) (֒to live֓ 0.471) (֒existence֓
0.471) (֒mind֓ 0.484) (֒to live֓ 0.486)
V (D
A
, ֒death֓, 7)=(֒death֓ 0) (֒murdered֓ 0.367) (֒killer֓ 0.377) (֒age of life֓ 0.481)
(֒tyrannicide֓ 0.516) (֒to kill֓ 0.579) (֒dead֓ 0.582)
Vectorial Sum. If X and Y are two vectors, their normalised vectorial sum V is defined
as :
ϑ
2
→ ϑ :V = X ⊕Y | V
i
=
X
i
+Y
i
kX +Yk
(4)
where ϑ is the set of the conceptual vectors, V
i
(resp X
i
, Y
i
) is the i-th component of
the vector V (resp. X, Y).
The normalized vectorial sum of two vectors gives a vector equidistant according to
the angle of the first two vectors. It is in fact an average the summoned vectors. As an
operation on the conceptual vectors, one can thus see the normalized vectorial sum as
the union of the ideas contained in the terms.
Normalised Term to Term Product. If X and Y are two vectors, their normalised term
to term product V is defined as :
ϑ
2
→ ϑ :V = X ⊗Y | v
i
=
√
x
i
y
i
(5)
The ⊗ operator can be interpreted as an operator of intersection between vectors. If
the intersection between two vectors is the null vector, then they do not have anything
in common. From the point of view of the conceptual vectors, this operation thus makes
it possible to select the ideas common to terms involved.
3.4 Construction of Vectors by Emergence
The approach by emergence is free from any thesaurus and vectors of concept as bases
departure. Only d the vector size is fixed a priori. The construction method of the
vectors is identical to the traditional model with the difference that if one of the vectors
entering the sum is non-existent, because not yet calculated, then this vector is drawn
randomly. The computing process is reiterated until convergence of each vector.
As we show in a more detailed way in [17], there is a certain number of advantages
to use this model. The first of them is to be able to freely choose the quantity of re-
sources which one wishes to use by choosing the size of the vectors in a suitable way.
To give an idea of the importance of this choice, a base of 500000 vectors of dimension
1000 is approximately 2Go, of size 2000, 4Go, ... As it would not be then reasonable
143

nor easy to define a concept set of the size chosen, It is easier to seek an approach which
enables us to avoid it. Moreover, what can seem a makeshift or at least a compromise
proves to be an advantage because the lexical density in space of the words calculated
by emergence is much more constant than in a space where concepts are predifined. In-
deed, the resources (dimensions of space) have tendency to be harmoniously distributed
according to the lexical richness.
4 Hybrid Modelisation of Meaning: Conceptual Vectors and
Lexical Networks
4.1 Contribution of the Lexical Networks to the Conceptual Vectors
As shown in [18], distances computed on vectors are influenced by shared components
and/or disinct components. Angular distance is a good tool for our aims because of
its mathematical characteristics, its simplicity to understand and to linguistically inter-
pret and futhermore it is effective for computational process. Whatever is the chosen
distance, used on this kind of vectors (represanting ideas and not term occurences), the
lower the distance is, the more the lexical objects are in the same semantic field (isotopy
as said by Rastier [19]).
In the framework of semantic analysis as the one which interests us, we use angu-
lar distance to benefit from mutual information carried by conceptual vectors to make
lexical disambiguation on words whose meanings are in close semantic fields. Thus,
”Zidane scored a goal.” can be disambiguated thanks to common ideas about sport
while ”The lawyer pleads at the court.” can be disambiguated thanks to those of jus-
tice. Furthermore, for prepositionnal attachments, vectors can permit in ”He saw the
girl with the telescope.” to attach ”with a telescope” to the verb ”saw” due to ideas
about vision.
On the contrary, conceptual vectors can’t be used to disambiguate terms which are
in different semantic fields. We can even note that an analysis only based on them can
lead to misinterpretation. For example, the French noun ֒avocat֓ has two meanings.
It is the equivalent of ֒lawyer֓ and the equivalent of ֒avocado֓. In the French sentence
”L’avocat a mang
´
e un fruit.”, ”The lawyer has eaten a fruit”, ֒to eat֓ and ֒fruit֓ carry
idea of ֒food֓ then the acception computed by conceptual vectors for ֒avocat֓ will be
֒avocado֓. It would have been necessary that the knowledge ”a lawyer is a human” and
”a human eats” can be identified, something that is not possible with only conceptual
vectors. Alone, they are not sufficient to exploit lexical functions instanciations in the
texts, a lexical network can thus contribute to correct these shortcomings. These limits
were shown in experiments for the semantic analysis using ant algorithms in [20].
4.2 Contribution of Conceptual Vectors to Lexical Networks
If they benefit of an unquestionable precision, the recall of networks is poor. It is, in-
deed, difficult to think that one could represent all the relations between the terms. In-
deed, how can we represent the fact that two terms are in the same semantic field? They
may be absent from the network because they may not be connected by ”traditional”
144

arcs. The introduction of arcs of the type ”semantic field” also seems problematic for
us because of two reasons implicated the fuzzy and flexible of this relation :.
– the first one is related to the database conceptor’s idea on this relation, when to
consider that two synsets are in the same semantic field? In an unfavourable case,
there would be very few arcs while in an opposite case we could have a combinative
explosion of the number of arc;
– the second problem, more fundamental, is related to representation itself. How to
plan to represent by a discrete element a fuzzy relation by essence of the continuous
field?
Thus, the continuous domain offered by conceptual vectors gives flexibilities that
the discrete domain offered by the networks cannot. They are able to bring closer words
on minority ideas but however common what it is not possible with a network. The
conceptual vectors and the operation of thematic distance can correct the weak recall
inherent of the lexical networks. The defects of the ones are thus mitigated by qualities
of the others what makes therefore conceptual vectors and lexical networks comple-
mentary tools.
5 Exp
´
erience on WordNet: Usage of Data
5.1 Exploitation of Definitions
EXtended WordNet [21] is a project carried out to Southern Methodist University of
Dallas (Texas, USA) which has two aims:
– to disambiguate terms used in the definitions of the synsets i.e. to indicate which
are the synsets employed in the definition;
– to transform these definitions into logical form to allow more easy calculations.
These data were built semi-automaticly using information from the network (for
example if the genus of the definition, within the meaning of Aristote, has a meaning
which is also an hyperonym of the defined synset, it is considered that the meaning of
the genus is this hyperonym), of distances between definitions or information about the
domain. These data are partly manually controlled and the rate of precision of more
than 90%.
For the conceptual vectors construction, we used these data as logical form because
they make it possible to locate the most important elements of the definition in par-
ticular the genus. Calculation is done thus on a dependency tree manufactured starting
from pretreated definition to remove the metalanguage not easily exploitable for a the-
matic analysis. In our explanations, we will use the example of the logical form of the
definition of ֒ant֓.
ant : NN(x1) −> social : JJ(x1) insect : NN(x1)live : VB(e1, x1,x3)
in : IN(e1,x2) organized : JJ(x2)colony : NN(x2)
There is 3 sets : x1 = {social, insect}, x2 = {organised, colony} and e1 = {live}.
This last and in make it possible to organise the sets as a hierarchy. The vector of each
145
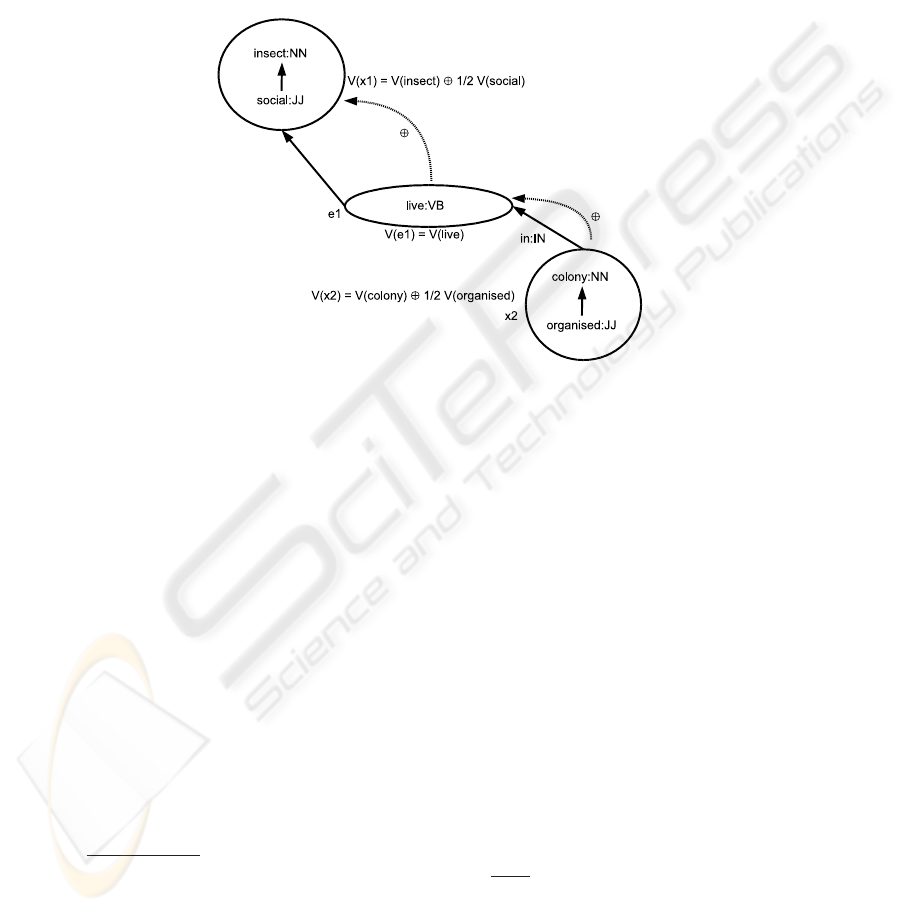
one of these sets is calculated making the vectorial sum of the item which carry most of
the meaning of this set (verbs, VB; nouns, NN) and half of the ones of the dependents
(adverbs, RB; adjectives, JJ). The computation of the global vector is done then by
weighted vectorial sum of the various sets in the tree in starting with the lowest part.
This mode of calculation makes it possible to consider in a dominating way the genus
on the other terms of the definitions and in a more general ways the heads on their
syntactic dependent. The figure 1 synthesizes this calculation. No predicate is the set x3
then it does not appears on the figure.
Fig.1. Construction of a conceptual vector from a definition: example of ant.
5.2 Exploitation of Relations
The exploitation of the relations is done at two level : (1) for the vector construction,
they build in a complementary way to the definitions the vector of a synset; (2) to avoid
phenomenon of regrouping of distinct sets.
Vectors Construction. The construction of a conceptual vector is done for each node
of the network by simple weighted normalised sum of the vectors of the linked nodes.
If N is a node linked to k nodes N
1
... N
k
, the vector of N is
V(N) = p
1
V(N
1
) + p
2
V(N
2
) + ... + p
k
V(N
k
) (6)
This approach naturally involves an agglomeration of the vectors. It is thus neces-
sary to increase the contrast of one vector following its computation. With this intention,
one calculates the coefficient of variation
4
of V. If this last is not around 10% of the
average CV the vector undergoes a nonlinear operation of amplification (exponentiation
of each component then normalisation), and this in a reiterated way until obtaining a
coefficient of variation in the acceptable values. This last was estimated starting from
predifined concepts.
4
the coefficient of variation CV is given by the formula
EC(V)
µ(V)
with EC(V) the standard deviation
of the vector V and µ(V) the arithmetic mean of the components of V.
146

Phenomenon of regrouping of distinct sets A last potential problem is that the vectors
of two distinct sets (at the same time for the lexical network and for thematic) of terms
can occupy the same area of space. Computation is done by activation and vectors are
randomly drawn at initialization, then that can occurs by accident. It is thus necessary
to ”separate” the close vectors but corresponding however to very different parts of the
lexical network and of thematic.
The phenomenon detection is done by examination of the neighbourhood of a con-
ceptual vector. If among the N first neighbors, the density of words with no correlation
with the target word is important then an action of separation must be undertaken.
This action of separation consists in plunging the whole network in field where
the nodes tend to be pushed back. In directly being inspired by physics, a force of
repulsion in 1/d
2
is calculated iteratively between nodes. For a given node, one can
thus calculate a vector displacement which will move away it from nodes to which it is
too near. Nodes not bringing closer by thematic neighbourhood (at the time of the first
phase of calculation cf. section 5.1) but being close ” accidently” end thus naturally up
separating.
6 Conclusion
In this article, we presented the conceptual vectors built by emergence. We showed in
what they can help to solve the tennis problem from their character complementary to
the lexico-semantic networks one whose most famous example in current research is
WordNet. Indeed, the recall of the networks is weak, they easily do not make it possible
to represent the semantic fields contrary to the vectors while the latter are not sufficient
to represent relations like hyperonymy or meronymy.
Our proposal is to benefit from this complementarity while adding to WordNet con-
ceptual vectors built starting from definitions and relations contained in this base. The
method suggested here holds of the continuous field contrary to the whole methods
we studied in the literature which belong to the discrete field (addition of arcs for the
relations, symbols about the domain, etc).
We are aware that this method only makes it possible to solve part of the problem
of tennis. Indeed, the conceptual vectors do not allow to exhib not-thematic colloca-
tionnal relationship between items. They are primarily the relations that Igor Mel’
ˇ
cuk
models with his syntagmatic lexical functions [22] like the intensification (”great fear”;
Magn (֒fear֓) = ֒great֓)), name of center (”crux of the problem”;Centr (֒problem֓) = ֒crux֓)
or even the confirmator(”legitimate excuse”; Ver (֒excuse֓) = ֒legitimate֓). As notices
[10], these relations belong to those which would probably be necessary to have in a
lexical base. We share this point of view, some tracks were explored in [23] and cur-
rently continue to be followed.
References
1. Quillian, R.: Semantic memory. In: Semantic Informatic processing. MIT Press (1968)
227–270
147

2. Mihalcea, R., Tarau, P., Figa, E.: Pagerank on semantic networks, with application toword
sense disambiguation. In: COLING’2004 : 20th International Conference on Computational
Linguistics, Geneva, Switzerland (2004) 1126–1132
3. Mangeot-Lerebours, M., S
´
erasset, G., Lafourcade, M.: Construction collaborative d’une base
lexicale multilingue : Le projet papillon. TAL (Traitement Automatique des langues) : Les
dictionnaires
´
electroniques 44 (2003) 151–176
4. Knight, K., Luk, S.: Building a large-scale knowledge base for machine translation. In:
AAAI’1994 : National Conference on Artificial Intelligence, Stanford University,Palo Alto,
California (1994)
5. Harabagiu, S., Chai, J., eds.: Usage of WordNet in Natural Language Processing Systems,
Universit
´
e de Montr
´
eal, Montr
´
eal, Canada (1998)
6. Fellbaum, C., ed.: WordNet: An Electronic Lexical Database. The MIT Press (1988)
7. Harabagiu, S.M., Miller, G.A., Moldovan, D.I.: Wordnet 2 - a morphologically and seman-
tically enhanced resource. In: Workshop SIGLEX’99 : Standardizing Lexical Resources.
(1999) 1–8
8. Agirre, E., Ansa, O., Martinez, D., Hovy, E.: Enriching wordnet concepts with topic signa-
tures. In: NAACL worshop on WordNet and Other Lexical Resources: Applications, Exten-
sions and Customizations, Pittsburg, USA (2001)
9. Stevenson, M.: Augmenting noun taxonomies by combining lexical similarity metrics. In:
COLING’2002 : 19th International Conference on Computational Linguistics. Volume 2/2.,
Taipei, Taiwan (2002) 953–959
10. Ferret, O., Zock, M.: Enhancing electronic dictionaries with an index based on associations.
In: Proceedings of the 21st International Conference on Computational Linguistics, Sydney,
Australia, Association for Computational Linguistics (2006) 281–288
11. Salton, G., McGill, M.: Introduction to Modern Information Retrieval. McGrawHill, New
York (1983)
12. Deerwester, S.C., Dumais, S.T., Landauer, T.K., Furnas, G.W., Harshman, R.A.: Indexing by
latent semantic analysis. Journal of the American Society of Information Science 41 (1990)
391–407
13. Chauch
´
e, J.: D
´
etermination s
´
emantique en analyse structurelle : une exp
´
erience bas
´
ee sur
une d
´
efinition de distance. TAL Information 31/1 (1990) 17–24
14. Larousse, ed.: Th
´
esaurus Larousse - des id
´
ees aux mots, des mots aux id
´
ees. Larousse (1992)
15. Kirkpatrick, B., ed.: Roget’s Thesaurus of English Words and Phrases. Penguin books,
London (1987)
16. Zock, M.: Sorry, what was your name again, or how to overcome the tip-of-the tongue with
the help of a computer? In: SemaNet’02: Building and Using Semantic Networks, Taipei,
Taiwan (2002)
17. Lafourcade, M.: Conceptual vector learning - comparing bootstrapping from a thesaurus or
induction by emergence. In: LREC’2006, Genoa, Italia (2006)
18. Besanc¸on, R.: Int
´
egration de connaissances syntaxiques et s
´
emantiques dans les
repr
´
esentations vectorielles de texte (2001)
19. Rastier, F.: L’isotopie s
´
emantique, du mot au texte (1985)
20. Lafourcade, M., Guinand, F.: Ants for natural language processing. International Journal of
Computational Intelligence Research (2006)
`
A para
ˆ
ıtre.
21. Mihalcea, R., Moldovan, D.: extended wordnet: progress report. In: NAACL 2001 - Work-
shop on WordNet and Other Lexical Resources, Pittsburgh, USA (2001)
22. Mel’
ˇ
cuk, I., Clas, A., Polgu
`
ere, A.: Introduction
`
a la lexicologie explicative et combinatoire.
Duculot (1995)
23. Schwab, D.: Approche hybride - lexicale et th
´
ematique - pour la mod
´
elisation, la d
´
etection
et l’exploitation des fonctions lexicales en vue de l’analyse s
´
emantique de texte. (2005)
148
