
KAT based CAD Model of Process Elements for Effective
Management of Process Evolution
Jeewani Anupama Ginige, Athula Ginige and Uma Sirinivasan
School of Computing and Mathematics, University of Western Sydney, Locked Bag 1797
Penrith South DC NSW 1797, Australia
Abstract. Processes consist of actions, participants, object and rules, known as
elements. In a process, these elements are inter-woven together to achieve de-
sired business goals. When managing process evolutions and changes, it is im-
perative to understand constraints, associations and dependencies (CAD)
among process elements. Use of high-level graphical model that encapsulate
CAD among process elements, as given in [1], is limited in practice. Therefore,
here we present formalism, to model CAD among process elements. This for-
malism is based on constraint modeling algebra named Kleene Algebra with
Tests (KAT) [2]. This paper gives a set of definitions to capture CAD among
process elements based on KAT. These definitions are used to create a single
compact KAT expression that captures all possible CAD among process ele-
ments. The holistic and cohesive nature in capturing CAD among process ele-
ments and deploying KAT to model them into a single expression are the
unique contributions of this research.
1 Introduction and Background
Business processes evolve and change to cater diverse needs. When processes are
automated, changes and evolutions need to be reflected in the automated systems
(workflows [3]). Changing a process means changing process elements - actions,
participants, object and rules. In a process, these elements do not exist in isolation.
To satisfy various business goals, elements are inter-woven and linked. Thus, making
a change (modifying, adding or removing) one element may result in propagating
impact on other elements. Therefore, it is important to have a mechanism to capture
various constraints, associations and dependencies (CAD) among process elements.
In this research, the focus is on exploring a formalism to capture CAD among
process elements. This work is presented as part of the solution of evolution meta-
model, which support the effective management process evolution in web-based
workflows systems (WWS) [4]. In this work, process evolution is discussed in rela-
tion to the framework of process automation [4]. Based on this framework, previously
we developed a graphical CAD model among process elements [1]. The work pre-
sented in this paper, extends our previous work by proposing a formalism to capture
CAD among process elements.
Anupama Ginige J., Ginige A. and Sirinivasan U. (2007).
KAT based CAD Model of Process Elements for Effective Management of Process Evolution.
In Proceedings of the 1st International Joint Workshop on Technologies for Collaborative Business Processes and Management of Enterprise
Information Systems, pages 13-22
DOI: 10.5220/0002435700130022
Copyright
c
SciTePress

The issue of reflecting process evolutions and changes in WWS is possibility of
making errors and inconsistencies, in implemented systems. The reasons for this are
twofold. First is the flexibility of the implementation of WWS. Second is the under-
stating and cohesive capturing CAD among process elements.
There are various process modeling tools such as Petri-nets [6], UML activity dia-
grams [7] and Event-driven Process Chains (EPC) [8]. However, most of these mod-
eling tools are geared to capture process for automation. Thus fails to capture some of
the CAD among process elements such as actions and data object [9, 10]. Apart form
Petri-nets, other modeling tools are not equipped to model constraints adequately.
Therefore, main purpose of this work is to find constraint modeling formalism, which
facilitates encapsulating CAD among process elements. Most importantly, such
mechanism should capture CAD among process elements, in a complete and cohesive
manner. Further, the possibility of presenting the process and associated CAD into a
single expression is preferred. Then this expression can be analyzed to understand the
impact of one element change to the rest of the process.
The rest of the paper is organized as follows. In section 2, we briefly recapture the
CAD model of process elements previously presented in [1]. In section 3, formalisms
are explored to find a suitable constraint modeling language, which leads to the intro-
duction Kleene Algebra (KA) and Kleene Algebra with Tests (KAT) [2]. Section 4
introduces a series of definitions based on KAT, to model CAD among process ele-
ments. In section 5, the use of of KAT expressions to find impact of process evolu-
tions is discussed. The section 6 identifies the significance of the work compared to
previous similar work. In conclusion, section 7 highlights possible future research
directions, arising from this work.
2 CAD Among Process Elements
The CAD among process elements have two facets; i) types of associations and ii)
constraints and conditions that affect the associations [1]. These are summarized
below and drawn upon from previous landmark research such as [11-19].
Types of Associations among Process elements are; i) among actions (A,A) –
sequential, parallel, conditional split, simple merge, multi merge, compensation and
skip. ii) between actions and participants (A,P) –obligation, permission and forbid-
dance. iii) between actions and data object (A,D) –visibility, interaction and routing.
iv) among data object elements (D,D) – integrity and computational relationships.
Constraints and conditions imposed on the associations among process elements
are; i) on the associations among actions C(A,A) –work item failures, deadline expiry,
external trigger, constraints violation, time constraints and external events. ii) on the
associations between actions and participants C(A,P)- location, experience, expertise
or skills, availability, workload and level of the organization structure, same or dif-
ferent sub structure, interpersonal relationships and reporting or delegation authori-
ties and history. and iii) on the associations between actions and data object C(A,D) -
personalization or ownership of information and specialization or extensions.
14

3 Kleene Algebra with Tests (KAT)
As mentioned previously the requirement is to find a formalism that allows capturing,
CAD among elements into a single and analytical expression. Therefore, below we
have analyzed to suitability of some of the prominent process modeling formalisms.
There are various formal methods used for process modeling purposes, for exam-
ple Process Algebra [20, 21] and Petri-Nets[22, 6]. While, use of Petri-nets for proc-
ess modeling is advocated, the inability to link to or refer to process data is consid-
ered to be one of the disadvantages of Petri nets [9]. In addition, Petri-nets alone do
not provide an algebraic structure that allows capturing CAD among process elements
into a single and analytical expression. The combination of Petri Nets with Process
Algebra, named to be Petri Nets Calculus (or Petri Box Calculus – PBC) attempts to
bring together the advantages both of Petri Nets and Process Algebra [23, 24]. How-
ever, the PBC does not provide a mechanism to capture the negation of a constraint,
which is applicable with the constraints identified above. On the other hand, the use
of Kleene Algebra (KA) and Kleene Algebra with Tests (KAT) [2] is promoted for
constraint based program modeling [25] and other application modeling purposes
[26]. Thus, here we experiment the use of KAT to model CAD among process ele-
ments.
The axioms KA and KAT as they are presented below. KA is an algebraic struc-
ture (K, +, · , * , 0 , 1) that satisfies the following axioms [2];
+ and · operators are associative Æ a + (b + c) = (a + b) + c and a(bc) = (ab)c
for all a, b, c in K
+ is commutative Æ a + b = b + a for all a, b in K
+ and · are distributive Æ a(b + c) = (ab) + (ac) and (b + c)a = (ba) + (ca) for all
a, b, c in K
for + and · there exists an element 0 in K such that for all a in K: a + 0 = 0 + a =
a and a0 = 0a = 0
for + and · there exists an element 1 in K such that for all a in K: a1 = 1a = a
for * there exists an elements 1 and
a in K such 1+aa* = a and 1+ a*a = a. In
other words * behaves like the Kleene Star operator in formal language theory.
KAT is a two-sorted algebraic structure (B, K, +, · , * , 0 , 1, ¬), where B is a sub-
set in K and ¬ is a unary operator, similar to negation, defined only on B such that (K,
+, · , * , 0 , 1) is a Kleene algebra and (B, +, · , ¬, 0 , 1) is a Boolean algebra [2].
Process actions are an integral part of a process. There are special characteristics
associated with process actions. For example, actions cannot be negative as compared
to conditions, in which the negation is valid. Also there is the possibility of certain
actions to be repeated [14]. The Kleene star operator * allows this iteration to be
modeled in combination with a guard condition to control the merging of parallel
branches. In KA dot operator is not commutative (only + is), thus could be used to
support two actions (say a
1
and a
2
) in sequence. This is written as a
1
a
2
since a
1
a
2
≠
a
2
a
1
according to KA axioms. Usually ‘dot’ operator is omitted in KAT expressions.
Looking at these characteristics, we define the following to present actions.
Definition 1: Process actions A {a
1
, a
2
, …, a
x
} is a subset of K with an algebraic
structure (K, A, +, · , * , 0 , 1) that satisfy the axioms of KA (defined above).
15
Usually a constraint is represented as a condition [26]. In conditions, it should be
possible to represent the negation. Thus the subset B of K, which is a defined to be a
Boolean algebra with the algebraic constructs (B, +, · , ¬, 0 , 1) can be utilized to
define these different constraints on the association among process elements. There-
fore, the definition below presents a mechanism to indicate constraints;
Definition 2: Constraints and conditions C {c
1
, c
2
, …, c
y
} is a subset of B with an
algebraic structure (B, C, +, · , ¬, 0 , 1) that satisfy the axioms of KA (defined be-
fore).
For this point onwards to denote actions and constraints, we use notations intro-
duced in definitions 1 and 2.
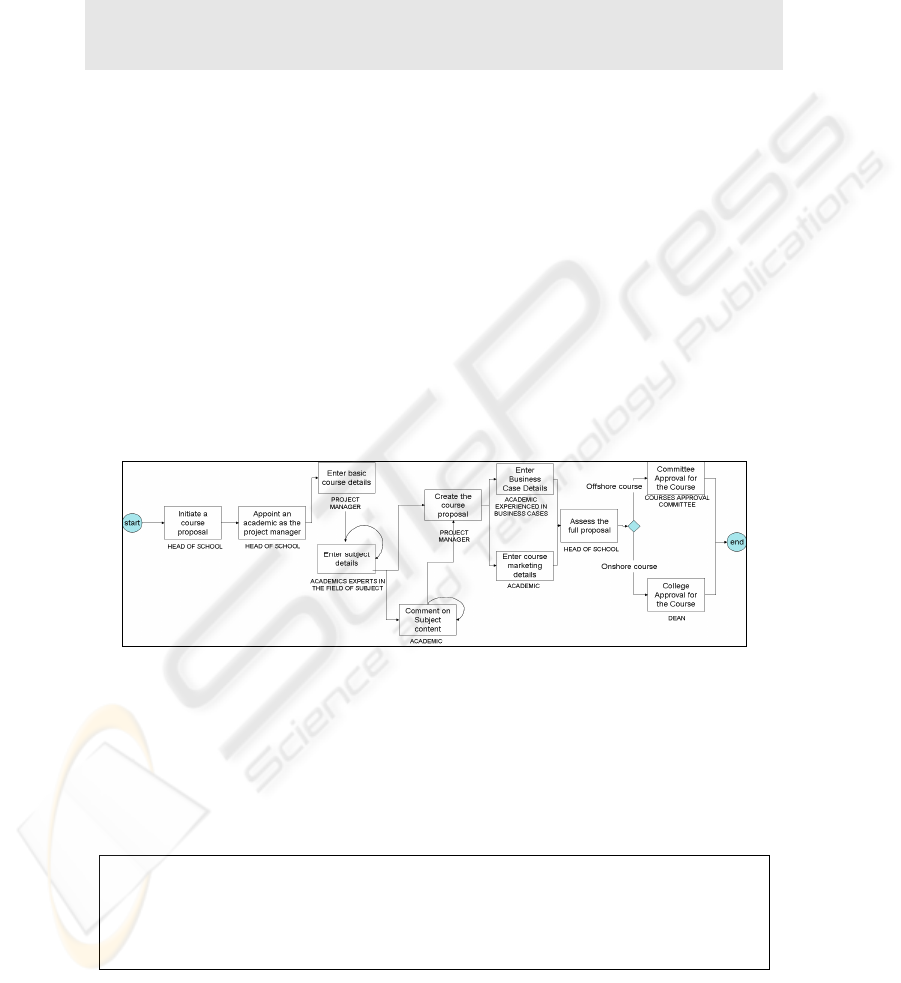
Let us consider an example to demonstrate the use of KAT in representing process
flow and various associations among process elements. Consider a typical course
creation example in a university environment, in which a course is proposed to be
offered (refer figure 1). In such a process, various academics would need to get in-
volved in filling in various types of data. This data would include basic course infor-
mation, information about subjects offered in this particular course, business case
details (to assess the financial viability of the course) and marketing information (in
order to publicize the course among potential students). In addition, various types of
checking, assessing and approval would be required. The figure 1 gives an illustration
of the process described above.
We have deliberately not used a specific standard modeling technique such as
UML, Petri nets or EPC to represent the example process in figure 1. The rationale
for this is to demonstrate the applicability of the KAT expressions to any process
irrespective of the modeling technique used.
Fig. 1. Example of a course creations and approval process.
The notations are simple and denote the following; boxes represent actions, the
role name below the box shows participants who perform the action. Arrow and dia-
mond shape respectively denote process flow and condition.
Actions related to figure 1, are defined in table 1 according to our Definition 1.
Table 1. Actions identified according to example in figure 2.
a
0
Æ Initiate a course proposal
a
1
Æ Appoint an academic as the project manager
a
2
Æ Enter basic course details
a
3
Æ Enter Subject details
a
4
Æ Comment on Subject content
a
5
Æ Create the full course proposal
a
6
Æ Enter business case details
a
7
Æ Enter course marketing details
a
8
Æ Assess the full course proposal
a
9
Æ Committee Approval for the course
a
10
Æ College Approval for the Course
16

First, we show the method to embed elements from K and B in a single expres-
sion. The definition below represents performing an action under a guard condition.
Definition 3: If a
x
represents an action and c
m
denotes a constraint the expression
c
m
a
x
indicates that a
x
can be performed iff the c
m
constraint is satisfied.
Next, more definitions are built on the foundation of Definitions 1 to 3 above.
4 KAT to Capture CAD among Process Elements
The definitions 4-7 below, demonstrate mechanisms to capture, various types of asso-
ciations that exist among process actions, identified as (A, A) in section 2.
The definition below represents the sequential representation between two actions
Definition 4: The sequential association between two action a
x
follows a
y
is repre-
sented as a
x
a
y
; denoting that
action a
y
can take place after a
x
is completed.
The following definition shows the conditional split between two actions.
Definition 5: The conditional choice between two-action a
x
or a
y
is represented as a
x +
a
y.
This denotes either action a
x
OR a
x
can be performed
The parallelism between two actions and multi merge is as follows.
Definition 6: The parallelism between two action a
x
follows a
y
is represented as (c
m
(a
x +
a
y
))*
.
In this c
m
presents the merging condition.
With the special element 1 є K skipping of a certain action is denoted as follows;
Definition 7: The construct to denote that action a
x
can be performed optionally is
written as; (a
x +
1). This means that either action a
x
can be performed or skipped as
required.
Based on the definitions 4 to 7 we will write the basic process model in KAT of
the above example in figure 1 (KAT expression 1). Note in this, the composite con-
straints are denoted using C
1
to C
14
. These guard conditions are progressively ex-
panded according to a new definitions introduced below.
Due to space limitations the rest of the types of associations among process ele-
ments and constraints on these associations are presented in the definitions 8-20, in
the table 2 below. The table also exemplifies the usage of this definition in relation to
the example given in figure 1.
The notations
c
1
to
c
32
captures CAD among process elements in relation to the ex-
ample in figure 1. In table 3, we demonstrate how these notations are used to create
composite conditions C
1
to C
14
, which were identified in the KAT Expression 1.
KAT Expression 1
(C
1
a
0
) (C
2
a
1
)(C
3
a
2
) C
4
(C
5
a
3
)*(C
6
(C
7
a
4
)*+1) (C
8
a
5
) (C
9
(C
10
a
6
+ C
11
a
7
)) * (C
12
a
8
)
(C
13
a
9
+
C
14
a
10
)
17

Table 2. More KAT definitions for CAD of process elements and examples from figure 1.
Type
of
CAD
KAT based Definitions
CAD among process elements identified in
relation to example in figure 1
(A, P)
Definition 8: c
n
Æ P do (role, action)
Definition 9: c
n
Æ O do (role, action)
Definition 10: c
n
Æ F do (role, action)
c
1
Æ P do (head of school, a
0
)
c
2
Æ O do (head of school, a
1
)
c
3
Æ O do (project manager, a
2
)
c
4
Æ O do (expert academic, a
3
)
c
5
Æ P do (academic, a
4
)
c
6
Æ O do (project manager, a
5
)
c
7
Æ O do (business case expert, a
6
)
c
8
Æ O do (academic, a
7
)
c
9
Æ O do (head of school, a
8
)
c
10
Æ P do (dean, a
9
)
c
11
Æ P do (course approval committee, a
9
)
(A, D)
Definition 11: c
n
Æ V ((data => {name
=>(reference), location => (database.table.attribute |
folder.document | database.table | class.object),
display=> (view| edit| hidden), format => ( textf |
texta| selection |check box |radio | label | report|
default)}), action)
Definition 12: c
m
ÆI ((data {reference1, reference2,
…}), action x, action y)
Definition 13: c
m
Æ RC (variable =>{reference},
operator =>{eq| gt| lt| el| eg}, value=> {any| 1|0| true|
false| yes | no})
c
12
ÆV((data=>{name=>{basic course details}, location =>
{course_approval.basic_course}, display=> {view}, for-
mat=>{report }, name=>{ responsibility }, location=>
{course_approval.staff_detail}, display=> {edit}, format
=>{selection}), a
1
)
Similar to above constraint notation c
12
, assume that there are
constraints c
13
to c
2`
, showing the visibility constraints for actions
a
2
to a
9
respectively.
c
22
Æ I((data{number of subjects, subject names=>{}, key
area=>{}), a
2
, a
3
)
c
23
Æ I ((data{first offering year}), a
1
, a
2
)
c
24
Æ RC (condition (variable =>{offshore }, operator =>{eq},
value=> {1}))
c
25
Æ RC (condition (variable =>{ number of loops }, operator
=>{eq}, value=> {number of subjects}))
(D, D)
Definition 14: c
m
Æ IC (subject component =>
{reference}, related components => { reference1,
reference2 , ...}, connector => {reference, reference,
..}, type of link => {foreign key | hyperlink | docu-
ment link })
Definition 15: c
m
Æ CC (subject component =>
{reference}, related components => { reference1,
reference2 , ...}, type of computation=> {summation |
average | other formula })
c
26
Æ IC (subject component => { basic course details }, related
components => { subject information }, connector =>
{course_name, course_code}, type of link => { foreign key })
c
27
Æ CC (subject component => { basic course information
.number of subjects }, related components => { subject informa-
tion }, type of computation=> {summation of number of sub-
jects})
c
28
Æ CC (subject component => { business case. Total cost },
related components => { staff costs, overheads, other costs, tax,
levy }, type of computation=> {summation })
C(A,A)
Definition 16: c
m
Æ TC (time reference => {abso-
lute | relative}, start time => {seconds: minutes:
hour: day: month: year| relative time}, end time => {
seconds: minutes: hour: day: month: year | time
period})
Definition 17: c
m
Æ XC (entity => {reference},
trigger => {reference})
This example does not contain any constraints under
these definitions
C(A,P)
Definition 18: c
m
Æ PC (role, characteristic (factor
=> {location| experience| expertise| skills| availabil-
ity| workload| level}, operator => {eq| gt| lt| el| eg | in
| not in | yes | no | is | is not}, value =>{ figure}))
Definition 19: c
m
Æ PC (role 1, role 2, (characteris-
tic (factor => {department| organizational unit| level |
personal relationships| delegate | report}, correlation
=> {same | different | yes | no | higher | lower}))
c
29
ÆPC(academic, characteristic (factor => {skill}, operator=>
{in}, value => {subject_details.key_area} ))
c
30
ÆPC(academic, characteristic (factor => { experience },
operator=>{in},value=>{ business case }))
c
31
Æ PC (academic, head of school, (characteristic (factor =>
{organizational unit }, correlation => {same}))
c
32
Æ PC (academic, dean, (characteristic (factor => { organiza-
tional unit }, correlation => {same}))
C(A,D)
Definition 20: c
m
Æ OC (characteristic =>
{ownership | specialization}, (identification =>
(object => {attribute reference}, specific value =>
{identification of the individual | specialization
details })))
This example does not contain any constraints under
these definitions
18

Table 3. Guard conditions of KAT Expression 1 according to the definitions given in Table 2.
Composite
guard element
Description According to the Dependencies Related to Example in Figure 2.
C
1
= c
1
Head of school is permitted to perform the subsequent action
C
2
= c
2
c
12
Head of school is obliged to perform the subsequent action AND use the action
interface definition referred by c
12
C
3
= (c
23
)
(c
3
c
31
c
13
)
Academic appointed as the project manager in the same school as the head of school
is obliged perform the subsequent action AND use the interface definition defined by
c
13
C
4
= c
22
c
25
A looping condition-based on the number_of_subjects captured in a
2
, the subsequent
action requires to be looped until data are filled for all subjects
C
5
= (c
4
c
31
)
(c
29
) (c
26
c
14
)
An academic in the same school as head of school and has got the special expertise
in the subject area can perform the subsequent action, using the interface definition
in c
14
C
6
= c
22
c
25
A looping condition -
based on the number_of_subjects captured in a
2
, the subse-
quent action requires to be looped until data are filled for all subjects
C
7
= (c
5
c
31
)
(c
15
)
An academic who is in the same school as head of school and has the special exper-
tise in the subject area can perform the subsequent action using the interface defini-
tion c
15
.
C
8
= (c
6
c
31
)
(c
26
c
16
)
An academic appointed as project manager AND in the same school as head of
school is allowed to perform the subsequent action, using the action interface defini-
tion c
16
C
9
Internal merge condition that looks whether both parallel actions are completed
C
10
= (c
7
c
31
)
(c
30
) (c
26
c
29
c
17
)
An academic who is in the same school as the head of school AND has the expertise
in the area of business cases is allowed to perform the subsequent action using data
set defined by c
27
and c
28
using the interface definition c
17
C
11
= (c
8
c
31
)
(c
26
c
18
)
An academic who is in the same school as the head of school allowed to perform the
subsequent action using data set defined by c
26
AND using the interface definition
c
18
C
12
= c
9
c
19
Head of school is obliged to perform the action using the interface definition c
19
C
13
= (¬c
24
(c
10
c
32
))(c
21
)
If the course is NOT off-shore a dean is in the same college as head of school is
allowed to perform the subsequent action using the interface definition c
21
C
14
= (c
24
(c
10
)
(c
21
))
If the course is offshore the chair of the courses approval committee is allowed to
perform the subsequent action using the action definition c
20
Thus, we can write the complete expanded version of KAT expression as follows;
(c
1
a
0
) (c
2
c
12
a
1
)((c
23
)(c
3
c
31
c
13
)a
2
) (c
22
c
25
)(((c
4
c
31
) (c
29
) (c
26
c
14
))a
3
)*((c
22
c
25
)(( (c
5
c
31
) (c
15
))
a
4
)*+1) (((c
6
c
31
) (c
26
c
16
))
a
5
) (C
9
(((c
7
c
31
) (c
30
) (c
26
c
29
c
17
) )a
6
+ ((c
8
c
31
) (c
26
c
18
))a
7
)) * ((c
9
c
19
)a
8
) (((¬c
24
(c
10
c
32
))(c
21
))a
9
+
((c
24
(c
10
) (c
21
)))a
10
)
KAT Expression 2
The KAT expression 2 represents a complete and cohesive set of dependencies
identified related to process in figure 1. However, the usage of expression on paper
for human is limited. In other words, it requires an data structure to capture above
expressions. Such a representation should capture all the semantics involved in the
structure of the expression and should be analytical. Space limitations in this paper do
not provide us opportunity to explore into such a construct.
19

5 Using Kat Expression to Locate the Impact of Evolution
Though it is not practical to analyze KAT expression 2 manually, here we conceptu-
ally demonstrate how it is done. Consider the change,“ It is no more required to cap-
ture the year of first offering in the course documents” due other business needs.
Now it let us analyze impact of this change on the process. By analyzing the list of
constraint definitions in table 3, we find that this data field is related to c
23
. Using this
as the starting point, below we present four types of impacts that could have on the
rest of the process;
• Direct impact – Actions that are directly affected or cannot be executed because
of the suggested change – highlighted in blue in the KAT expression 3.
• Indirect impact – Actions that that has cannot be researched because of the
direct impact – highlighted in yellow in KAT expression 3 (since action a
2
is
prior to other actions in a sequential ordering of actions)
• Secondary impact – Actions that may be performed but unable to merge with
the main flow due to the direct impact – These kind of impact are not present due
this particular change
• Cautionary impact – Actions that can be performed but requires checking to
assure the accuracy – highlighted in green in the KAT expression 3.
(c
1
a
0
) (c
2
c
12
a
1
) ((c
23
)(c
3
c
31
c
13
)a
2
) (c
22
c
25
)(((c
4
c
31
) (c
29
) (c
26
c
14
))a
3
)*((c
22
c
25
)(( (c
5
c
31
) (c
15
))
a
4
)*+1) (((c
6
c
31
) (c
26
c
16
))
a
5
) (C
9
(((c
7
c
31
) (c
30
) (c
26
c
29
c
17
) )a
6
+ ((c
8
c
31
) (c
26
c
18
))a
7
)) * ((c
9
c
19
)a
8
)
(((¬c
24
(c
10
c
32
))(c
21
))a
9
+
((c
24
(c
10
) (c
21
)))a
10
)
KAT Expression 3
6 Similar Work
The similarity or difference of previous work against this research is hard to measure
in one dimension. The main objective of this work is to support web-based workflow
evolution, by means of capturing process element CAD among process elements into
a single formal expression. The highlighted words are the key areas that this research
is associated.
There are number of research works, such as [17, 18, 27-29], that aim to support
process evolution. In these researches, the term evolution is used synonym to dyna-
mism, flexibility, adaptability, etc. In addition, the approaches used for making work-
flows evolvable are different in each of these works. In particular, the works [17, 28]
approaches are somewhat similar to our work, in which the constraints and dependen-
cies among process elements are considered in supporting process evolution.
There are various researches aimed at capturing process elements associations,
constraints and dependencies such as [12-19]. However in most of this works the
objective for capturing process constraints is different from our main goal of support-
ing web based workflow evolution. Therefore, the identification of various con-
straints, associations and dependencies among process elements are presented in
varying degrees in these researches. Nevertheless, Sadiq et al’s work on specification
20

and validation of process constraints for flexible workflows, bares certain similarities
to our work, in identifying CAD among process elements [17]. However, the signifi-
cance of our work is using KAT for cohesive capturing of CAD among process ele-
ments.
7 Conclusion and Future Research Directions
This paper aims to support the issue of managing the process evolution in web-based
workflows. In particular, here we introduce the importance of understanding various
CAD among process elements, in order to locate the impact of one change to the rest
of the process.
The approach used here is to represent CAD among process elements using a set
of KAT based definitions. The KAT based definitions allows capturing CAD among
process elements into a single expression. Though a practical application was not
presented in relation to impact resolution, the method of locating impact of one
change to the rest of the process using KAT expressions was demonstrated in con-
cept.
As the future research of this work, the foremost important one would be to im-
plement a system that allows creating and analyzing KAT expressions to find the
process element changes to the rest of the workflow. Secondly, it would be advanta-
geous to validate the exhaustiveness of the dependencies identified in section 2, based
on process examples of other domains.
References
1. J. A. Ginige, A. Ginige, and U. Sirinivasan, "Towards Effective Management of Process
Evolution in Web-based Workflows: Dependencies and Constraints Model of Process Ele-
ments," Melbourne Australia, 2007 (Accepted).
2. D. Kozen, "Kleene Algebra with Tests," ACM, pp. 17, 1999.
3. WfMC, "Workflow Management Coalition - Terminology & Glossary." Winchester,
Hampshire, United Kingdom: Workflow Management Coalition, Feb 1999, pp. 8-9.
4. J. A. Ginige and A. Ginige, "Meta-Model for Tracing Impact of Contextual Information
Evolution in Web-based Workflows," presented at 9th International Conference on Enter-
prise Information Systems (ICEIS 07), Funchal, Madeira - Portugal, 2007.
5. W. M. P. van der Aalst, "Verification of Workflow Nets," Application and Theory of Petri
Nets, vol. 1248, pp. 407–426, 1997.
6. W. M. P. van der Aalst, K. M. van Hee, and G. J. Houben, "Modelling and analysing work-
flow using a Petri-net based approach," presented at Proc. 2 ndWorkshop on Computer-
Supported Cooperative Work, Petri nets and related formalisms, 1994.
7. J. W. Schmidt, "A Comparison of Event-driven Process Chains and UML Activity Diagram
for Denoting Business Processes," D. I. A. Wienberg, Ed. Harburg: Technische Universität
Hamburg-Harburg, 2001.
8. J. Mendling, G. Neumann, and M. Nuttgens, "Towards Workflow Pattern Support of
Event-Driven Process Chains (EPC)," presented at 2nd Workshop XML4BPM, 2005.
9. E. Oren and A. Haller, "Formal frameworks for workflow modelling," DERI-Digital Enter-
prise Research Institute, vol. 20, 2005.
21

10. W. M. P. van der Aalst, M. Weskez, and G. Wirtz, "Advanced Topics in Workflow Man-
agement: Issues, Requirements, and Solutions," Integrated Design and Process Science,
vol. Volume 7, pp. pp 49-77, 2003.
11. R. Lu, S. Sadiq, V. Padmanabhan, and G. Governatori, "Using a temporal constraint net-
work for business process execution," Proceedings of the 17th Australasian Database Con-
ference-Volume 49, pp. 157-166, 2006.
12. O. Marjanovic, "Dynamic Verification of Temporal Constraints in Production Workflows,"
Proceedings of the 11th Australian Database Conference, vol. 7481, 2000.
13. N. Russell, A. H. M. ter Hofstede, D. Edmond, and W. M. P. van der Aalst, "Workflow
data patterns," presented at 24th Int. Conf. on Conceptual Modeling (ER05), 2005.
14. N. Russell, A. H. M. ter Hofstede, W. M. P. van der Aalst, and N. Mulyar, "WORKFLOW
CONTROL-FLOW PATTERNS A Revised View," BPMcenter.org 2006.
15. N. Russell, W. M. P. van der Aalst, and A. H. M. ter Hofstede, "Workflow Exception Pat-
terns," 2006.
16. N. Russell, W. M. P. van der Aalst, A. H. M. ter Hofstede, and D. Edmond, "Workflow
Resource Patterns: Identification, Representation and Tool Support," presented at 17th
Conference on Advanced Information Systems Engineering (CAiSE’05), 2005.
17. S. W. Sadiq, M. E. Orlowska, and W. Sadiq, "Specification and validation of process con-
straints for flexible workflows," Information Systems, vol. 30, pp. 349-378, 2005.
18. W. Sadiq, O. Marjanovic, and M. E. Orlowska, "Managing Change and Time in Dynamic
Workflow Processes," IJCIS, vol. 9, pp. 93-116, 2000.
19. W. M. P. van der Aalst, A. H. M. ter Hofstede, B. Kiepuszewski, and A. P. Barros, "Work-
flow Patterns," Distributed and Parallel Databases, vol. 14, pp. 5-51, 2003.
20. J. Camara, C. Canal, J. Cubo, and A. Vallecillo, "Formalizing WSBPEL Business Proc-
esses Using Process Algebra," Proceedings of FOCLASA, 2005.
21. H. Smith and P. Fingar, "Workflow is just a Pi process," Computer Sciences Corporation
2003.
22. W. M. P. van der Aalst, K. M. Hee, and K. V. Hee, Workflow Management: Models, Meth-
ods, and Systems: Mit Pr, 2002.
23. J. Hall, The High Level Petri Box Calculus: Basic Concepts: University of York, Dept. of
Computer Science, 1993.
24. B. Mikolajczak, "Review of Petri Net Algebra," ACM SIGACT News, vol. 33, pp. 10-14,
2002.
25. D. Kozen, "Kleene algebra with tests, Transactions on Programming Languages andSys-
tems " ACM, pp. 427–443, 1997.
26. K. D. Schewe and B. Thalheim, "Conceptual modelling of web information systems," Data
and Knowledge Engineering, vol. 54, pp. 147–188, 2005.
27. G. Vossen, M. Weske, and G. Wittkowski, "Dynamic Workflow Management on the Web,"
Fachbericht Angewandte Mathematik und Informatik, vol. 24, pp. Last accessed on
10/03/2005 from http://dbms.uni-muenster.de/staff/weske/papers/fb24-96.ps.gz, 1996.
28. J. Wainer, F. Bezerra, and P. Barthelmess, "Tucupi: a flexible workflow system based on
overridable constraints," presented at Proceedings of the 2004 ACM symposium on Ap-
plied computing, 2004.
29. D. Wang, Y. A. N. Xiu-Tian, W. J. Ion, W. Runxiao, et al., "An Approach to a Web-based
Flexible Workflow Modeling," presented at ASR '2005 Seminar, Instruments and Control,
Ostrava, April 29, 2005, 2005.
22
