VISUAL SOFTWARE MODELLING WITH EXTENDED

RULE-BASED MODEL

A Knowledge-based Programming Solution for General Software Design

Grzegorz J. Nalepa and Igor Wojnicki

Institute of Automatics, AGH – University of Science and Technology, Al. Mickiewicza 30, 30-059 Kraków, Poland

Keywords:

Rule-based programming, software modelling, knowledge engineering, automated implementation, XTT.

Abstract:

Rule-based programming paradigm is omnipresent in number of engineering domains. However, there are

some fundamental semantical differences between it, and classic procedural, or object-oriented approaches.

Even though, there has been a lot of effort to use rules to model business logic in classic software no generic

solution has been provided so far. In this paper a new approach for generalized rule-based programming

is given. It is based on a use of advanced rule representation, which includes an extended attribute-based

language, a non-monotonic inference strategy, with explicit inference control on the rule level. The paper

shows how some typical programming constructions, as well as classic programs can be modelled in this

approach. The approach can largely improve both the design and the implementation of complex software.

1 INTRODUCTION

Rule-based programming paradigm is omnipresent in

number of engineering domains such as control and

reactive system, diagnosis and decision support. Re-

cently, there has been a lot of effort to use rules to

model business logic in classic software. However,

there are some fundamental semantical differences

between it, and classic procedural, or object-oriented

approaches. This is why no generic modelling solu-

tion has been provided so far.

The motivation of this paper is to investigate the

possibility of modelling typical programming struc-

tures with an extended forward-chaining rule-based

programming. In this paper a new approach for gen-

eralized rule-based programming is given. It is based

on a use of an advanced rule representation, which in-

cludes an extended attribute-based language (Lig˛eza,

2006), a non-monotonic inference strategy, with ex-

plicit inference control on the rule level. The pa-

per shows, how typical programming constructions

(such as loops), as well as classic mini-programs

(such as factorial) can be modelled in this approach.

It presents possibilities of efﬁcient integration of this

technique with existing software systems.

The paper is composed of several parts. In Sect. 2

basics of the rule-based programming are given, and

in Sect. 3 fundamental differences between software

and knowledge engineering are given. Then, in

Sect. 4 the extended model for rule-based systems

is considered. The application of this model is dis-

cussed in Sect. 5. This model could be integrated in a

classic software system in several ways, considered

in Sect. 6. The research presented in this paper is

a work-in-progress. Some directions for the future

research as well as concluding remarks are given in

Sect. 7.

2 RULE-BASED PROGRAMMING

Rule-Based Systems (RBS) constitute a powerful AI

tool (Negnevitsky, 2002) for speciﬁcation of knowl-

edge in design and implementation of systems in the

domains such as system monitoring and diagnosis,

intelligent control, and decision support. For the

state-of-the-art in RBS see (Liebowitz, 1998; Jack-

son, 1999; Lig˛eza, 2006). From a point of view of

classical knowledge engineering (KE) a rule-based

expert system consists of a knowledge base and an in-

ference engine. The KE process aims at designing and

evaluating the knowledge base, and implementing the

J. Nalepa G. and Wojnicki I. (2007).

VISUAL SOFTWARE MODELLING WITH EXTENDED RULE-BASED MODEL - A Knowledge-based Programming Solution for General Software

Design.

In Proceedings of the Second International Conference on Evaluation of Novel Approaches to Software Engineering , pages 41-47

DOI: 10.5220/0002586600410047

 SciTePress

inference engine. The process of building the knowl-

edge base involves the selection of a knowledge rep-

resentation method, knowledge acquisition, and pos-

sibly low-level knowledge encoding. In order to cre-

ate an inference engine a reasoning technique must be

selected, and the engine has to be programmed.

In the formal analysis of RBS (Lig˛eza, 2006)

some important aspects of the design and implemen-

tation are identiﬁed. The ﬁrst concerns rulebase de-

sign, including: the formal logical language of the

representation, formal syntax of the representation

method, representation expressiveness, which is re-

lated to the expressiveness of the underlying logic,

and particular rule syntax. The second comes down

to the inference engine implementation, including:

inference strategy, interpreter model, including rule

matching method, and conﬂict resolution algorithm.

In order to design and implement a RBS in an

efﬁcient way, the knowledge representation method

should support the designer, introducing a scalable vi-

sual representation. As the number of rules exceeds

even relatively very low quantities, it is hard to keep

the rule-base consistent, complete, and correct. These

problems are related to knowledge-base veriﬁcation,

validation, and testing. To meet security requirements

a formal analysis and veriﬁcation of RBS should be

carried out (Vermesan and Coenen, 1999). This anal-

ysis usually takes place after the design stage. How-

ever, there are design and implementation methods,

such as the XTT, that allow for on-line veriﬁcation

during the design and gradual reﬁnement of the sys-

tem.

Supporting rulebase modelling remains an essen-

tial aspect of the design process. In this area number

of approaches are present. The simplest one consists

in writing rules in the low-level RBS language, such

as one of Jess (www.jessrules.com). A more so-

phisticated approaches are based on the use of some

classic visual rule representations. This is a case of

LPA VisiRule, (www.lpa.co.uk) which uses decision

trees. Approaches such as XTT (Nalepa, 2004) aim at

developing a new language for visual rule modelling.

While RBS found wide range of industrial appli-

cations in „classic AI domains” e.g. decision support,

system diagnosis, or intelligent control, the technol-

ogy did not ﬁnd applications in the mainstream soft-

ware engineering – due to some fundamental differ-

ences between knowledge and software engineering.

3 SOFTWARE AND

KNOWLEDGE ENGINEERING

Rule-based systems (RBS) constitute today one of

the most important classes of the so-called Knowl-

edge Based Systems (KBS). Building real-life KBS

is a complex task. Since their architecture is fun-

damentally different from classic software, typical

Software Engineering approaches cannot be applied

efﬁciently. Some speciﬁc development methodolo-

gies, commonly referred to as Knowledge Engineer-

ing (KE), are required.

What makes KBS distinctive is the separation of

knowledge storage (the knowledge base) from the

knowledge processing facilities. In order to store

knowledge, KBS use various knowledge representa-

tion methods, which are declarative in nature. In case

of RBS these are production rules. Speciﬁc knowl-

edge processing facilities, suitable for particular rep-

resentation method being used, are selected then. In

case of RBS these are logic-based inference engines.

The knowledge engineering process, involves two

main tasks: knowledge base design, and inference en-

gine implementation. Furthermore, other tasks are

also required, such as: knowledge base analysis and

veriﬁcation, and inference engine optimization. The

performance of a complete RBS should be evaluated

and validated. While this process is speciﬁc to expert

systems, it is usually similar in case of other KBS.

What is important about the process, is the fact

that it should capture the expert knowledge and rep-

resent it in a way that is suitable for processing (this is

the task for a knowledge engineer). The actual struc-

ture of a KBS does not need to be system speciﬁc – it

should not „mimic” or model the structure of the real-

world problem. However, the KBS should capture

and contain knowledge regarding the real-world sys-

tem. The task of programmers is to develop process-

ing facilities for the knowledge representation. The

level at which KE should operate is often referred

to as the knowledge level (Newell, 1982). It should

be pointed out, that in case of KBS there is no sin-

gle universal engineering approach, or universal mod-

elling method (such as UML in software engineer-

ing). Different classes of KBS may require speciﬁc

approaches, see (Lig˛eza, 2006; Torsun, 1995).

Software engineering (SE) is a domain where a

number of mature and well-proved design methods

exist; furthermore, the software development process

and its life cycle is represented by several models.

One of the most common models is called the water-

fall model (Sommerville, 2004). In the software engi-

neering process a number of development roles can be

identiﬁed: users and/or domain experts, system ana-

ENASE 2007 - International Conference on Evaluation on Novel Approaches to Software Engineering

lysts, programmers, testers, integrators, and end users

(customers). What makes this process different from

knowledge engineering is the fact that systems ana-

lysts try to model the structure of the real-world infor-

mation system in the structure of computer software

system. So the structure of the software corresponds,

to some extent, to the structure of the real-world sys-

tem. Then programmers encode and implement the

model (which is the result of the system analysis) in

some lower-level programming language.

The important difference between SE and KE, is

that the former tries to model how the system works,

while the latter tries to capture and represent what is

known about the system. The knowledge engineering

approach assumes that information about how the sys-

tem works can be inferred automatically from what is

known about the system (Nalepa, 2005).

The fundamental differences between the KE and

SE approaches include:

• declarative vs. procedural point-of-views,

• clear semantic gaps in the SE process, between

the requirements, design, and implementation,

• the application of gradual abstraction as the main

approach to the design of KBS.

The solution introduced in this paper aims at integrat-

ing a classic KE methodology of RBS with SE. The

model considered here, based on the XTT method

could serve as an effective bridge between SE and KE.

4 EXTENDED RULE-BASED

MODEL

The approach considered in this paper is based on

an extended rule-based model. The model uses the

XTT knowledge method with certain modiﬁcations.

The XTT method was aimed at forward chaining rule-

based systems. In order to be applied to general

programming it is modiﬁed in several aspects. Fur-

thermore, it proved to be robust and highly effective

combining features of decision tables and decision

trees (Nalepa, 2004).

4.1 XTT – Extended Tabular Trees

The XTT (EXtended Tabular Trees) knowledge repre-

sentation (Nalepa, 2004; Nalepa and Lig˛eza, 2005a),

has been proposed in order to solve common design,

analysis and implementation problems with RBS. In

this method three representation levels are addressed:

• visual – the model is represented by a hierarchical

structure of linked extended decision tables,

A1 An −X +Y H

a11 a1n x1 y1 h1

am1 amn xm ym hm

Figure 1: A single XTT table.

• logical – tables correspond to sequences of ex-

tended decision rules,

• implementation – rules are processed using a Pro-

log representation.

On the visual level the model is composed of ex-

tended decision tables. A single table is presented in

Fig. 1. The table represents a set of rules, having the

same attributes.

A rule can be read as follows:

IF (A11 ∈ a11) ∧ .. .(A1n ∈ a1n) T HEN

retract(X = x1), assert(Y = y1),do(H = h1).

It includes two extensions compared to classic RBS:

• non-atomic attribute values, used both in condi-

tions and decisions,

• non-monotonic reasoning support, with dynamic

assert, retract operations in decision part.

Every table row corresponds to a decision rule. Rows

are interpreted from the top row to the bottom one.

Tables can be linked in a graph-like structure. A link

is followed when rule (row) is ﬁred.

There are tools (see (Nalepa, 2004; Nalepa and

Lig˛eza, 2005b))which support the design process us-

ing the above visual model. They are capable of deﬁn-

ing attributes, creating linked XTT tables, and last but

not least running the inference process. There is also

an ongoing research to make these tools cover func-

tionality presented in Sect. 4.2.

On the logical level a table corresponds to a num-

ber of rules, processed in a sequence. If a rule is ﬁred

and it has a link, the inference engine processes the

rule in another table. The rule is based on a attribu-

tive language (Lig˛eza, 2006).

It corresponds to a Horn clause:

¬p

∨ ¬p

∨ ... ∨ ¬p

∨ h

where p is a literal in SAL (set attributive logic)

(see (Lig˛eza, 2006)) in a form:

(o) ∈ t

where o ∈ O is a object referenced in the system, and

∈ A is a selected attribute of this object (property),

VISUAL SOFTWARE MODELLING WITH EXTENDED RULE-BASED MODEL - A Knowledge-based Programming

Solution for General Software Design

t ⊆ D

is a subset of attribute domain A

. Rules are

interpreted using a uniﬁed knowledge and fact base,

that can be dynamically modiﬁed during the infer-

ence process using Prolog-like assert/retract operators

in rule decision.

Rules are implemented using Prolog-based repre-

sentation (see (Nalepa and Lig˛eza, 2006)). Rule rep-

resentation uses Prolog terms, which is a very ﬂexi-

ble solution. However, it requires a dedicated meta-

interpreter (Covington et al., 1996; Bratko, 2000).

This model has been successfully used to model

classic rule-based expert systems. For the needs of

general programming described in this paper, some

important modiﬁcations are proposed.

4.2 XTT Enhancements

Considering the use of XTT for general appli-

cations, there have been several extensions pro-

posed regarding the base XTT model. These are:

Grouped Attributes, Attribute-Attribute Comparison,

Not-Deﬁned Operator, Link Labeling, Scope Opera-

tor, Multiple Rule Firing. Applying these extensions

constitute the XTT Plus (or XTT+ for short).

Grouped Attributes provide means for putting to-

gether some number of attributes to express relation-

ships among them and their values. As a result a com-

plex data structure, called a group, is created which

is similar to constructs present in programming lan-

guages (i.e. C language structures).

A group is expressed as:

Group(Attrinbute1, Attribute2,... ,AttributeN)

Attributes within a group can be referenced by

their name: Group.Attribute1 or position within the

group: Group/1. An application of such Grouped

Attributes could be expressing spatial coordinates:

Position(X,Y ) where Position is the group name, X

and Y are attribute names.

The Attribute-Attribute Comparison concept in-

troduces powerful mechanism to the existing XTT

comparison model. In addition to comparing an at-

tribute value against a constant (Attribute-Value Com-

parison) it allows for comparing an attribute value

against another attribute value.

The Attribute-Value Comparison can be expressed

as a condition:

if (Attribute OPERATOR Value) then ...

where OPERATOR is a comparison operator i.e. equal,

greater then, less than etc., while Attribute-Attribute

Comparison is expressed as a condition:

if (Attribute1 OPERATOR Attribute2) then ...

where OPERATOR is a comparison operator or a func-

tion in a general case:

if (OPERATOR(Att1,...,AttN)) then ...

The proposed Not-Deﬁned (N/D) operator checks

if a value for a given attribute has been deﬁned. It has

a broad application regarding modelling basic pro-

gramming structures, i.e. to make a certain rule ﬁred

if the XTT table can be executed for the ﬁrst time.

The Link Labeling concept allows to reuse certain

XTTs, which is similar to subroutines in procedural

programming languages. Such a reused XTT is ex-

ecuted in several contexts. There are incoming and

outgoing links. Links are labeled, if control comes

from a labeled link it has to be directed through an

outgoing link with the same label. There can be mul-

tiple labeled links for a single rule then. If an outgo-

ing link is not labeled it means that if a corresponding

rule is ﬁred the link will be followed regardless of the

incoming link label. Such a link (or links) might be

used to provide control for exception-like situations

or making a set of XTTs reusable.

The graphical Scope Operator provides a basis for

modularized knowledge base design. It allows for

treating a set of XTT as a certain Black Box with well-

deﬁned input/output. Outside the given scope only

conditional attributes for the incoming links and con-

clusion attributes for the outgoing links are visible.

Scope Operators make the knowledge base more

scalable and it provides modularity. Furthermore it al-

lows rule management at the scope level, managing a

given scope, or set of scopes. This includes checking

rule consistency within a given scope.

Since multiple values for a single attribute are al-

ready allowed, it is worth pointing out the the new in-

ference engine being developed treats them in a more

uniform and comprehensive way. If a rule is ﬁred and

the conclusion or assert/retract use a multivalue at-

tribute such a conclusion is executed as many times

as there are values of the attribute. It is called Mul-

tiple Rule Firing. This behavior allows to perform

aggregation or set based operations easily.

5 MODELLING SOFTWARE

WITH RULES

The XTT+ can be applied in other domains than RBS.

The section presents typical programming constructs

developed using the XTT+ model.

5.1 Basic Programming Structures

Two main constructs considered here are: a condi-

tional statement, and a loop. Programming a condi-

tional with rules is both simple and straightforward,

ENASE 2007 - International Conference on Evaluation on Novel Approaches to Software Engineering

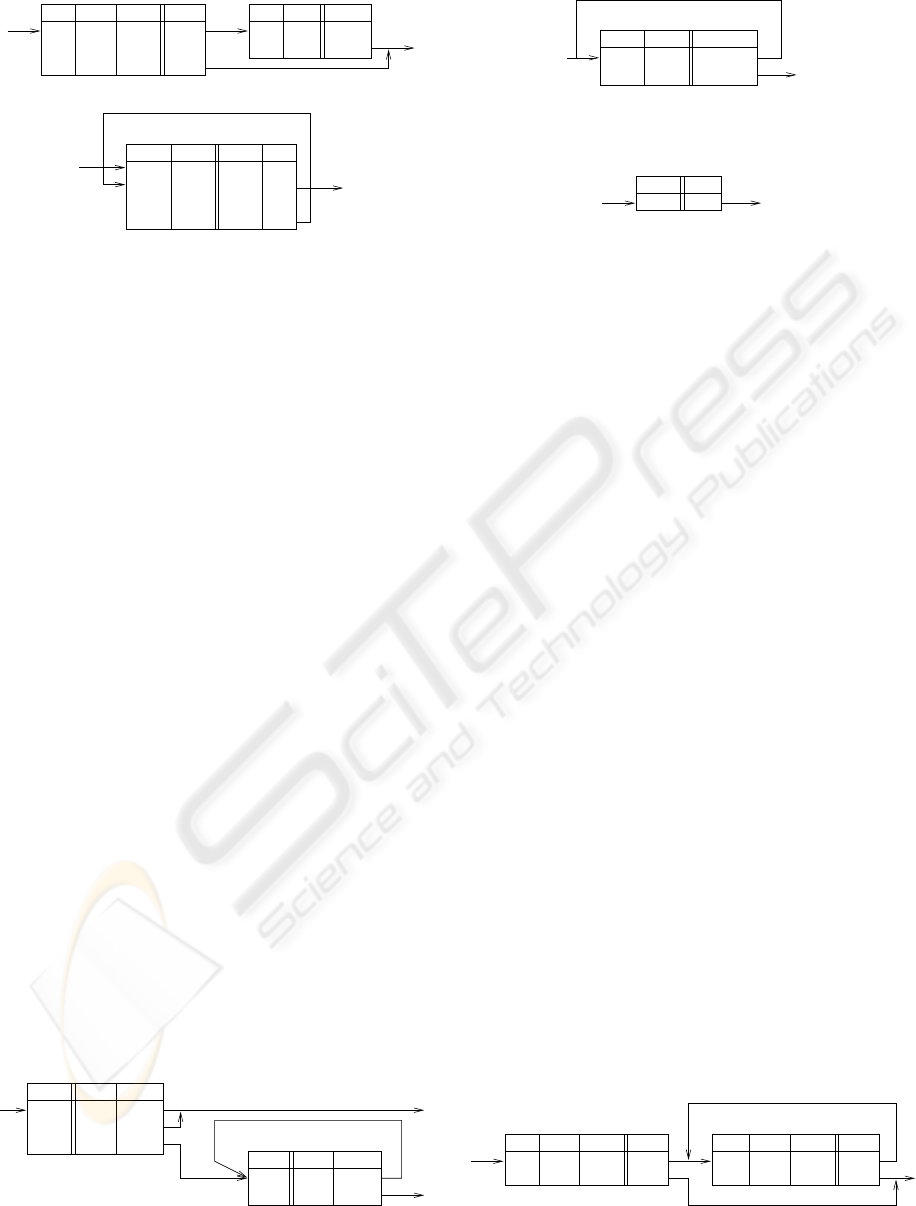
F G

ANY

+F FC

ANY

else then

ANY

h1 f4

Figure 2: A conditional statement.

while

ANY

N/D

ANY ANY

=I+1

ANY

ANYANYc h

Figure 3: A loop statement.

since a rule is by deﬁnition a conditional statement. In

Fig. 2 two table system is presented. The ﬁrst row of

the else table represents the main conditional state-

ment using attribute C, while the remaining rows im-

plement the statements executed on attributes G and F

when the condition is not met. If the condition is met,

then the other table, simply called then is executed.

A loop can be easily programmed, using the dy-

namic fact base modiﬁcation feature. In Fig. 3 a

simple system implementing the for-like loop is pre-

sented. In the XTT table the initial execution, as well

as the subsequent ones are programmed. The I at-

tribute serves as the index. In the body of the loop the

value of the decision attribute Y is modiﬁed depend-

ing on the value of the conditional attribute X. The

loop ends when the index value is greater then Z. This

could be easily generalized into the while loop.

5.2 Simple Programming Cases

A set of rules to calculate a factorial is given in Fig. 4.

An argument is given as attribute X. The calculated

result is given as Y . The iterative algorithm is imple-

mented which uses S attribute as a counter.

Since an attribute can be assigned more than a sin-

gle value (i.e. using the assert feature), certain op-

erations can be performed on such a set (It is sim-

ilar to aggregation operations regarding Relational

Databases). An example of sum function is given in

Fig. 5. It adds up all values assigned to X and stores

the result as the value of Sum attribute. The logic be-

N/D

factorial0

N/D

factorial1

Y S

=Y*S =S−1

ANY N/D

Figure 4: Factorial implementation.

sum

Sum

ANY

Sum

N/D =0

ANY ANY =Sum+X

Figure 5: Sum implementation.

ANY

copy

Figure 6: Copying elements of a set.

hind is as follows. If Sum is not deﬁned then make it

0 and loop back. Than, the second rule is ﬁred, since

Sum is already set to 0. The conclusion is executed as

many times as values are assigned to X . If Sum has a

value set by other XTTs prior to the one which calcu-

lates the sum, the result is increased by this value.

Assigning a set of values to an attribute based on

values of another attribute is given in Fig. 6. The

given XTT populates Y with all values assigned to X .

It uses the XTT assert feature.

Using XTT even complex task such as browsing a

tree can be implemented easily. A set of XTTs ﬁnding

successors of a certain node in a tree is given in Fig.7.

It is assumed that the tree is expressed as group of

attributes t(P,N), where N is a node name, and P is

a parent node name. The XTTs ﬁnd all successors of

a node which name is given as a value of attribute P

(it is allowed to specify multiple values here). A set

of successors is calculated as values of F. The ﬁrst

XTT (labeled tree1) computes immediate child nodes

of the given one. If there are any child nodes control is

passed to the XTT labeled tree2. It ﬁnds child nodes

of the children computed by tree1 and loops over to

ﬁnd children’s children until no more child nodes can

be found. The result is stored as values of F.

6 MODEL INTEGRATION

The XTT+ has been discussed on the conceptual level

of the visual representation. Two approaches to pro-

vide a runtime environment are considered.

The ﬁrst one consists in generating native code in

t.P t.N

ANY

N/D

=t.N

t.N +F

=t.N

t.PF

=F ANY

=F N/D ANYANY

ANY

tree1 tree2

ANY

Figure 7: Finding successors in a tree.

VISUAL SOFTWARE MODELLING WITH EXTENDED RULE-BASED MODEL - A Knowledge-based Programming

Solution for General Software Design

an object-oriented language such as Java. This solves

both the practical implementation as well as runtime

problem. This solution is used in products such as

JBoss Rules (formerly Drools). However, it does has

a major drawback: the object-oriented semantics is

very distant from the declarative rule semantics of

XTT+. This instantly unveils a semantic gap which

turns out to be a major limitation during the imple-

mentation and testing of the system. Furthermore,

while a translation from XTT+ to object-oriented if

fairly simple, a reversed one is complicated.

The second approach is based on using a high

level Prolog representation of XTT. Prolog seman-

tics includes all of the concepts present in the XTT+.

It has the advantages of ﬂexible symbolic repre-

sentation, as well as advanced meta-programming

facilities (Covington et al., 1996; Bratko, 2000).

The XTT+-in-Prolog solution is based on the Pro-

log implementation, presented in (Nalepa and Lig˛eza,

2006). In this case a term-based representation is

used, with an advanced meta interpreter engine pro-

vided. There are two ways of the integration of

the Prolog-based XTT+ model with a Java applica-

tion. The ﬁrst one consists in linking the Prolog-

based XTT+ interpreter with a Java application us-

ing Prolog-to-Java interface provided for some ad-

vanced Prolog implementations, such as SWI (www.

swi-prolog.org). In this approach the SWI Prolog

JPL interface is being used to communicate from the

Prolog programs with Java objects. Another one re-

lies on the idea of embedding the whole interpreter in

a Java application, with use of Java-based Prolog in-

terpreters. So far the JIProlog (www.ugosweb.com/

jiprolog) has been considered.

Furthermore, the integration could be considered

on an architectural level. The idea is to use the Mode-

View-Controller (MVC) pattern (Burbeck, 1992). In

this case the XTT+ would be used to build the ap-

plication logic model, where-as other parts of the ap-

plication, mainly the interface could be built with

object-oriented languages such as Java. The appli-

cation logic interfaces with object-oriented compo-

nents. These components provide means for inter-

action with environment which is user interface and

general input-output operations. It is also possible to

extend the model with arbitrary code. There are sev-

eral scenarios possible regarding interactions between

the model and the environment. In general, they can

be subdivided into output and input schemas. These

schemas provide view and controller functionalities.

The input schema takes place upon checking con-

ditions required to ﬁre a rule. A condition may re-

quire input operations. A state of such a condition is

determined by the data from the environment. Such

a data could be user input, ﬁle contents, a state of an

object, a result from a function. The input operation

could be blocking or non-blocking providing basis for

synchronization with environment. The input schema

acts as the controller regarding the MVC approach.

The output schema takes place if a conclusion re-

gards an output operation. In such a case the opera-

tion regard general output (i.e. through user interface),

spawning a method or function, setting a variable etc.

A conclusion also carries its state which is true or

false depending on whether the output operation suc-

ceeded or failed respectively. If the conclusion fails,

the rule fails as well. The output schema acts as the

view regarding the MVC approach.

7 CONCLUDING REMARKS

Rule-based programming paradigm plays an impor-

tant role in number of engineering domains. The fun-

damental semantical differences between it, and clas-

sic programming approaches do not allow for using it

to model business logic in classic software.

In the paper the research in the ﬁeld of knowl-

edge and software engineering is presented. The re-

search aims at the uniﬁcation of knowledge engineer-

ing methods with software engineering. The paper

presents a new approach for generalized rule-based

programming called XTT+. It is based on the use of

advanced rule representation, which includes an ex-

tended attribute-based language, a non-monotonic in-

ference strategy, with explicit inference control.

The original contribution of the paper consists in

the extension of the XTT rule-based systems knowl-

edge representation method, into XTT+, a more gen-

eral programming solution; as well as the demon-

stration how some typical programming constructions

and classic programs can be modelled in this ap-

proach. Furthermore XTT+ is fully integrable with

existing object-oriented programming languages such

as Java. The integration is provided based on the

Model-View-Controller concept. Future work will be

focused on representation extensions and use cases.

The original XTT has been applied to control sys-

tems, and selected security systems. The application

of XTT+ will be also extended towards business rules

systems, with richer semantics.

In its current stage, XTT+ can successfully model

number of programming constructs and approaches.

This proves XTT+ can be applied as a general pur-

pose programming environment. However, the re-

search should be considered an experimental one, and

deﬁnitely a work in progress.

ENASE 2007 - International Conference on Evaluation on Novel Approaches to Software Engineering

ACKNOWLEDGEMENTS

The paper is supported by the HEKATE Project

funded from 2007–2008 resources for science as a re-

search project.

Research supported from AGH University Grant

No.: 11.11.120.44

REFERENCES

Bratko, I. (2000). Prolog Programming for Artiﬁcial Intel-

ligence. Addison Wesley, 3rd edition.

Burbeck, S. (1992). Applications programming in

smalltalk-80(tm): How to use model-view-controller

(mvc). Technical report, Department of Computer

Science, University of Illinois, Urbana-Champaign.

Covington, M. A., Nute, D., and Vellino, A. (1996). Prolog

programming in depth. Prentice-Hall.

Jackson, P. (1999). Introduction to Expert Systems.

Addison–Wesley, 3rd edition. ISBN 0-201-87686-8.

Liebowitz, J., editor (1998). The Handbook of Applied Ex-

pert Systems. CRC Press, Boca Raton.

Lig˛eza, A. (2006). Logical Foundations for Rule-Based Sys-

tems. Springer-Verlag, Berlin, Heidelberg.

Nalepa, G. J. (2004). Meta-Level Approach to Integrated

Process of Design and Implementation of Rule-Based

Systems. PhD thesis, AGH University of Science and

Technology, AGH Institute of Automatics, Cracow,

Poland.

Nalepa, G. J. (2005). Rule-based systems design and im-

plementation : methodologies and technologies. In

Ryszard Tadeusiewicz, Antoni Lig˛eza, M. S., editor,

CMS’05. Plenary lectures and special session papers

: Computer Methods and Systems, volume 1, pages

329–340, Kraków, Poland. AGH University of Sci-

ence and Technology Cracow, Jagiellonian University,

Cracow University of Technology, Oprogramowanie

Naukowo-Techniczne.

Nalepa, G. J. and Lig˛eza, A. (2005a). A graphical tabular

model for rule-based logic programming and veriﬁca-

tion. Systems Science, 31(2):89–95.

Nalepa, G. J. and Lig˛eza, A. (2005b). A visual edition tool

for design and veriﬁcation of knowledge in rule-based

systems. Systems Science, 31(3):103–109.

Nalepa, G. J. and Lig˛eza, A. (2006). Prolog-based anal-

ysis of tabular rule-based systems with the xtt ap-

proach. In Sutcliffe, G. C. J. and Goebel, R. G., ed-

itors, FLAIRS 2006: proceedings of the 19th interna-

tional Florida Artiﬁcial Intelligence Research Society

conference, pages 426–431. AAAI Press.

Negnevitsky, M. (2002). Artiﬁcial Intelligence. A Guide to

Intelligent Systems. Addison-Wesley, Harlow, Eng-

land; London; New York. ISBN 0-201-71159-1.

Newell, A. (1982). The knowledge level. Artiﬁcial Intelli-

gence, 18(1):87–127.

Sommerville, I. (2004). Software Engineering. Interna-

tional Computer Science. Pearson Education Limited,

7th edition.

Torsun, I. S. (1995). Foundations of Intelligent Knowledge-

Based Systems. Academic Press, London, San Diego,

New York, Boston, Sydney, Tokyo, Toronto.

Vermesan, A. and Coenen, F., editors (1999). Validation

and Veriﬁcation of Knowledge Based Systems. The-

ory, Tools and Practice. Kluwer Academic Publisher,

Boston.

VISUAL SOFTWARE MODELLING WITH EXTENDED RULE-BASED MODEL - A Knowledge-based Programming

Solution for General Software Design