ARTIFICIAL NEURAL NETWORKS FOR DIAGNOSES OF

DYSFUNCTIONS IN UROLOGY

David Gil Mendez,

Magnus Johnsson,

Antonio Soriano Paya and

Daniel Ruiz Fernandez

Computing Technology and Data Processing, University of Alicante, Spain

Lund University Cognitive Science & Dept. of Computer Science, Lund University, Lund, Sweden

Keywords:

Artiﬁcial neural networks, urology, artiﬁcial intelligence, medical diagnosis, decision support systems.

Abstract:

In this article we evaluate the work out of artiﬁcial neural networks as tools for helping and support in the

medical diagnosis. In particular we compare the usability of one supervised and two unsupervised neural

network architectures for medical diagnoses of lower urinary tract dysfunctions. The purpose is to develop a

system that aid urologists in obtaining diagnoses, which will yield improved diagnostic accuracy and lower

medical treatment costs. The clinical study has been carried out using the medical registers of patients with

dysfunctions in the lower urinary tract. The current system is able to distinguish and classify dysfunctions as

areﬂexia, hyperreﬂexia, obstruction of the lower urinary tract and patients free from dysfunction.

1 INTRODUCTION

Nowadays, the urologists have different tools avail-

able to obtain urodynamical data. However, it still re-

mains very complicated to make a correct diagnosis:

the knowledge concerning the origin of the detected

dysfunctions depends mainly on acquired experience

and on the research, which is constantly carried out

within the ﬁeld of urology. The specialists in urology

are quite often dealing with situations that are poorly

described or that are not described in the medical lit-

erature. In addition there are numerous dysfunctions

whose precise diagnoses are complicated. This is a

consequence of the interaction with the neurological

system and the limited knowledge available on how

this operates.

Various techniques are used to diagnose dysfunc-

tions of the lower urinary tract (LUT), which en-

tail different degrees of invasiveness for the patient

(Abrams, 2005). A urological study of a patient con-

sists of carrying out various costly neurological as

well as physical tests like ﬂowmetry and cystometry

examinations with high degrees of complexity and in-

vasiveness. This project is intended to aid the special-

ist in obtaining a reliable diagnosis with the small-

est possible number of tests. To this end we propose

the use of artiﬁcial neural networks (ANNs) since

these present good results for classiﬁcation problems

(Begg, 2006). The reason why we decided to ap-

ply ANNs instead of other artiﬁcial intelligence (AI)

methods for the support of medical diagnosis is due

to the fact that ANNs can be trained with appropri-

ate data learning in order to improve their knowledge

of the system. In comparison to other techniques or

other (more classical) approaches such as rules based

systems or probabilities, ANNs are more suitable for

medical diagnosis. On one hand, rules based systems

(MYCIN system (Mycyn, 1976)) contain ”if-then”

rules where the ”if” side of any rule is a collection

of one or more conditions connected by logical oper-

ators such as ”AND”, ”OR” and ”NOT”. On the other

hand, other systems such as probability systems cal-

culate measures of conﬁdence without the theoretical

underpinnings of probability theory. These formal ap-

proaches based on probability theories are precise but

can be awkward and non-intuitive to use.

Therefore, in medical diagnosis, we use the advan-

tages of ANNs, which are considered as a method

of disease classiﬁcation. This classiﬁcation has two

divergent meanings. We can have a set of registers,

vectors or data with the aim of establishing the exis-

tence of classes or clusters. In contrast, we can know

with certainty that there exist some classes, and the

aim is to establish a rule able to classify a new regis-

ter into one of these classes. The ﬁrst type is known

as Supervised Learning and the second one is known

as Unsupervised Learning (or Clustering). We believe

that the accuracy of the diagnosis in medicine and, in

particular, in urology will be improved by using these

types of architectures (one supervised and two unsu-

191

Gil Mendez D., Johnsson M., Soriano Paya A. and Ruiz Fernandez D. (2008).

ARTIFICIAL NEURAL NETWORKS FOR DIAGNOSES OF DYSFUNCTIONS IN UROLOGY.

In Proceedings of the First International Conference on Health Informatics, pages 191-196

 SciTePress

pervised).

With the system of aid to the diagnosis major ben-

eﬁts are obtained both for the patient, by avoiding

painful tests, and for the medical centres by avoid-

ing expensive urodynamical tests and reducing wait-

ing lists.

Although the use of ANNs in medicine is a rather

recent phenomenon, there are many applications de-

ployed as in the ﬁeld of diagnosis, imaging, pharma-

cology, pathology and of course prognosis. ANNs

have been used in the diagnosis of appendicitis, back

pain, dementia, myocardial infraction (Green, 2006),

psychiatric disorders (Peled, 2005)(Politi, 1999),

acute pulmonary embolism (Suzuki, 2005), and tem-

poral arteries.

In Urology,prostate cancer serves as a good exam-

ple of the usability of ANNs (Remzi, 2001)(Batuello,

2001)(Remzi, 2004). However our work is more re-

lated with the neurological part which is less explored

(Gil, 2006)(Gil, 2005)(Ruiz, 2005).

In this paper we describe the implementations of

ANN based systems aiming at support diagnoses of

dysfunctions of the LUT. The remaining part of the

paper is organized as follows: ﬁrst, we give a brief

description of the employed neural network architec-

tures. Next we describe the design of our proposal

and the training of the ANNs by the available data.

Then we describe the subsequent testing carried out

in order to analyze the results. Finally we draw the

relevant conclusions.

2 NEURAL NETWORK

ARCHITECTURES

We have tested three different neural network archi-

tectures, two unsupervised ANNs and one supervised

ANN. The goal is to obtain a system that supports the

diagnoses of the dysfunctions of the LUT. The clas-

siﬁcation in the maps of the unsupervised ANNs and

the output from the supervised ANN will assist the

urologist in their medical decisions.

2.1 Supervised ANN - Multilayer

Perceptron

A typical Multilayer perceptron (MLP) network con-

sists of three or more layers of neurons: an input layer

that receives external inputs, one or more hidden lay-

ers, and an output layer which generates the classiﬁ-

cation results (Jiang, 2006)(Fig. 2). Note that unlike

other layers, no computation is involved in the input

layer. The principle of the network is that when data

are presented at the input layer, the network neurons

run calculations in the consecutive layers until an out-

put value is obtained at each of the output neurons.

This output will indicate the appropriate class for the

input data.

The architecture of the ANN (MLP) consists of

layer 1, with the inputs that correspond to the input

vector, the layer 2, with the hidden layer and the layer

3 which are the outputs (the 3 diagnoses of the LUT)

and the learning used is backpropagation and the al-

gorithm runs as follows:

All the weight vectors m are initialized with small

random values from a pseudorandom sequence gen-

erator. The following steps are repeated until conver-

gence (i.e. when the error E is below a preset value):

Update the weight vectors m

m(t + 1) = m(t) + ∆m(t) (1)

where

∆m(t) = −h∂E(t)/∂m (2)

Compute the error E(t+1).

where t is the iteration number,m is the weight vector,

and h is the learning rate. The error E can be chosen

as the mean square error function between the actual

output y

and the desired output d

E =

∑

j= 1

− y

)

(3)

Input

Hidden

Output

Figure 1: The architecture of the MLP.

2.2 Unsupervised ANN - Kohonen’s

Self-Organizing Maps

Kohonen’s Self-Organizing Map (SOM) is com-

posed of neurons located in a two-dimensional matrix

(Kohonen, 1988)(Kohonen, 1990)(Kohonen, 2000).

There is a weight vector, m

= (m

i1 i2

... m

) asso-

ciated with every neuron in the SOM, where n is the

dimension of the input vectors. In our case they are

the n ﬁelds of each observation of a pattern or a pa-

tient in the register.

The SOM is used as a classiﬁer and is organized

as indicated in ﬁgure 1.

In the fully trained network each neuron is asso-

ciated with a vector in the input space. The SOM is

a soft competitive neural network, which means the

winner neuron, i.e. the neuron with the weight vec-

tor that is closest to the current input vector according

to some measure (dot product in our implementation),

gets its weight vector updated so that it becomes more

similar to the input vector. The neurons in the vicin-

ity of the winner neuron also get their weight vec-

tors updated but to a lesser extent. Usually a Gaus-

sian function of the distance to the winner neuron is

used to modify the updating of the weight vectors.

The trained SOM is a projection of the input space,

which preserves the topological relationships of the

input space. The training of the SOM works as fol-

lows:

At time step t an input signal x ∈ R

activates a

winner neuron c for which the following is valid:

∀i : x

(t)m

(t) ≥ x

(t)m

(t) (4)

The weights are updated according to:

(t + 1) =

(

(t) +α(t)x(t)]

||m

(t) +α(t)x(t)||

if i ∈ N

(t)

(t) if i /∈ N

(t)

(5)

where N

(t) is the neighbourhood of the neuron c at

time t and 0 < α(t) < ∞.

Input Vector

{x1...xn}

Reference Vector

{mi1...min}

Figure 2: The Kohonen SOM.

2.3 Unsupervised ANN - Growing Cell

Structures

It has been pointed out that the predeﬁned structure

and size of Kohonen’s SOM bring limitations to the

resulting mapping. One attempt to solve this prob-

lem is the growing cell structures (GCS) (Fritzke,

1993)(Fritzke, 1997), which has a ﬂexible and com-

pact structure, a variable number of elements and a k-

dimensional topology where k can be arbitrarily cho-

sen.

In principle, the adaptation of a weight vector in

the GCS is done as described in the previous sec-

tion (SOM), i.e. determine the best matching neu-

ron, adjust its weight vector and the weight vectors of

its topological neighbours. However, there are two

important differences when compared to the SOM,

namely that the adaptation strength is constant over

time, and that only the best matching neuron and its

direct topological neighbours are adapted.

The GCS estimates the probability density func-

tion P(x) of the input space by the aid of local signal

counters that keep track of the relative frequency of

input signals gathered by each neuron. These esti-

mates are used to indicate proper locations to insert

new neurons. The insertion of new neurons by this

method will result in a smoothing out of the relative

frequency between different neurons. The advantages

of this approach is that also the topology of the net-

work will self-organize to ﬁt the input space and the

proper number of neurons for the network will be au-

tomatically determined, i.e. the algorithm stops when

a certain performance criterion is met. Another ad-

vantage is that the parameters are constant over time.

The basic building block and also the initial con-

ﬁguration of the GCS is a k-dimensional simplex.

Such a simplex is for k = 1 a line, for k = 2 a triangle,

and for k = 3 a tetrahedron. In our implementation

k = 2.

The self-organizing process of the GCS works as

follows:

The network is initialized to contain k + 1 neurons

with weight vectors m

∈ R

randomly chosen. The

neurons are connected so that a k-dimensional sim-

plex is formed.

At time step t an input signal x ∈ R

activates a

winner neuron c for which the following is valid:

∀i : ||x − m

|| ≥ ||x − m

|| , (6)

and the squared distance between the input signal and

the winner neuron c is added to a local error variable

∆E

= ||x − m

. (7)

The weight vectors are updated by fractions ε

and ε

respectively according to:

∆m

= ε

(x− m

) (8)

∀i ∈ N

: ∆m

= ε

(x− m

), (9)

where N

is the set of direct topological neighbours of

c. A neuron is inserted if the number of input signals

that have been generated so far is an integer multi-

ple of a parameter λ. This is done by dividing the

longest edge between the neuron q with the largest

accumulated error and its connected neighbour f, and

then removing the earlier connection (q, f) and con-

nect r to all neighbours that are common for q and

f. The weight vector for r is interpolated from the

weight vectors for q and f:

= (m

+ m

)/2. (10)

The error variables for all neighbours to r are de-

creased by a fraction α that depends on the number

of neighbours of r:

∀i ∈ N

: ∆E

= (−α/|N

|) · E

, (11)

The error variable for r is set to the average of its

neighbours:

= (1/|N

|) ·

∑

ι∈Nr

, (12)

and then the error variables of all neurons are de-

creased:

∀i : ∆E

= −βE

(13)

3 EXPERIMENTATION

An exhaustive urological exploration with 21 differ-

ent measurements has been carried out with 200 pa-

tients with dysfunctions of the lower urinary tract in

order to create a database. The data has been analyzed

and processed before entered into the network to en-

sure that it is homogenized. These 200 registers con-

tribute to the full knowledge adding different values

to delimit the ranks of each measure. Each of these

registers contains the information measured in the 21

ﬁelds showed in Table 1. For this reason, this database

plays a crucial role in order to obtain the knowledge

base of our system.

The table 1 shows the ﬁelds (every variable) of the

urological database (their physical units and types of

data). This table helps us to understand the dimension

of the problem to deal with (different types of data,

ranges and incomplete ﬁelds). The column direction

of the table indicates the meaning for the ANN: all the

ﬁelds are input for the system except the ﬁeld diagno-

sis, which is the dysfunction of each register. There

are three dysfunction and one output more for the di-

agnosis free of dysfunction.

Our database presents a diversity of ranks, values

and types. For this reason it is better to start with a

process of discretization in order to ﬁnd a way to guar-

antee the homogeneity as a ﬁrst step in the process

of training of the ANN. It was adjusted and weighted

with the help of the urologists, following their instruc-

tions and suggestions.

For example, some of the ﬁelds of the database are

age, volume of urine and micturition time (as can be

seen in table 1). As the differences among all these

ﬁelds are huge, we created ranks in the values of the

Table 1: The ﬁelds of the urological database.

Variable Type of data Values Direction

Age Numerical 3 85 years Input

Sex Categorical Male, female Input

Neurological Physical Examination

Perineal and peri-

anal sensitivity

Categorical Partial, absence,

normal, weak

Input

Voluntary control

anal sphincter

Categorical Partial, absence,

normal, weak

Input

Anal tone Categorical Normal, relaxed Input

Free Flowmetry

Volume of urine Numerical 7 682 ml Input

Maximum ﬂow

rate

Numerical 4 58 ml/s Input

Medium ﬂow Numerical 1 43 ml Input

Post void residual Numerical 0 550 ml Input

Micturition time Numerical 13 160 s Input

Cystometry

Bladder storage Numerical 50 461 ml Input

First sensation of

bladder ﬁlling

Numerical 50 300 ml Input

Detrusor pressure

during ﬁlling

Numerical 2 30 cm H20 Input

Test pressure / ﬂow

Detrusor contrac-

tion

Categorical Invol., Vol.,

Invol.-Vol.

Input

Volume of urine

in micturition

Numerical 0 556 ml Input

Maximum

pressure Detrusor

Numerical 2 200 cm H20 Input

Average ﬂow rate Numerical 0 10 ml/s Input

Abdominal pres-

sure

Categorical Yes, no Input

Post void residual Numerical 0 350 ml Input

Maximum ﬂow

rate

Numerical 0 31ml/s Input

Micturition time Numerical 2 318 s Input

Diagnosis

Areﬂexia, Hyperreﬂexia, Obstruction of the LUT, No

Dysfunction

Output

ﬁelds dividing them into subclasses in order to adjust

the data input.

For instance:

Age: 0-20 (1), 21-50 (2), 51-65 (3), >65 (4)

Volume of urine: 0-150 (1), 151-300 (2), 301-500

(3), >500 (4)

The numbers between the parentheses are the dis-

cretized representations. As we can observe the difﬁ-

culties are not only in the data ranks, but also in the

types of data, which complicates the process of data

discretization.

The next step is to run the experimentation.

This has been performed by using cross-validation

method. The data has been divided in ﬁve sets (S1,

S2, S3, S4, S5) and the ﬁve experiments performed

were:

Experiment 1-Training: T1, T2, T3, T4; Test: V (S5)

Experiment 2-Training: T1, T2, T3, T5; Test: V (S4)

Experiment 3-Training: T1, T2, T4, T5; Test: V (S3)

Experiment 4-Training: T1, T3, T4, T5; Test: V (S2)

Experiment 5-Training: T2, T3, T4, T5; Test: V (S1)

Experiment 1

Experiment 5

Figure 3: Cross Validation method.

This method is represented in ﬁgure 3. There are

four data sets used for the process of constructing the

model (the training data). The other set of data used

to validate the model (the test data). The test data are

chosen randomly from the initial data and the remain-

ing data form the training data. The method is called

5-fold cross validationsince this process has been per-

formed ﬁve times.

The results of the Multilayer Perceptron with

the backpropagation algorithm are of around 80%

of accuracy. For the other networks, the unsuper-

vised ones, the results are of 76% for the Grow-

ing Cell Structures and 74% for Kohonen’s Self-

Organizing Map. The MLP offers a slightly better

performance than GCS and SOM. However the unsu-

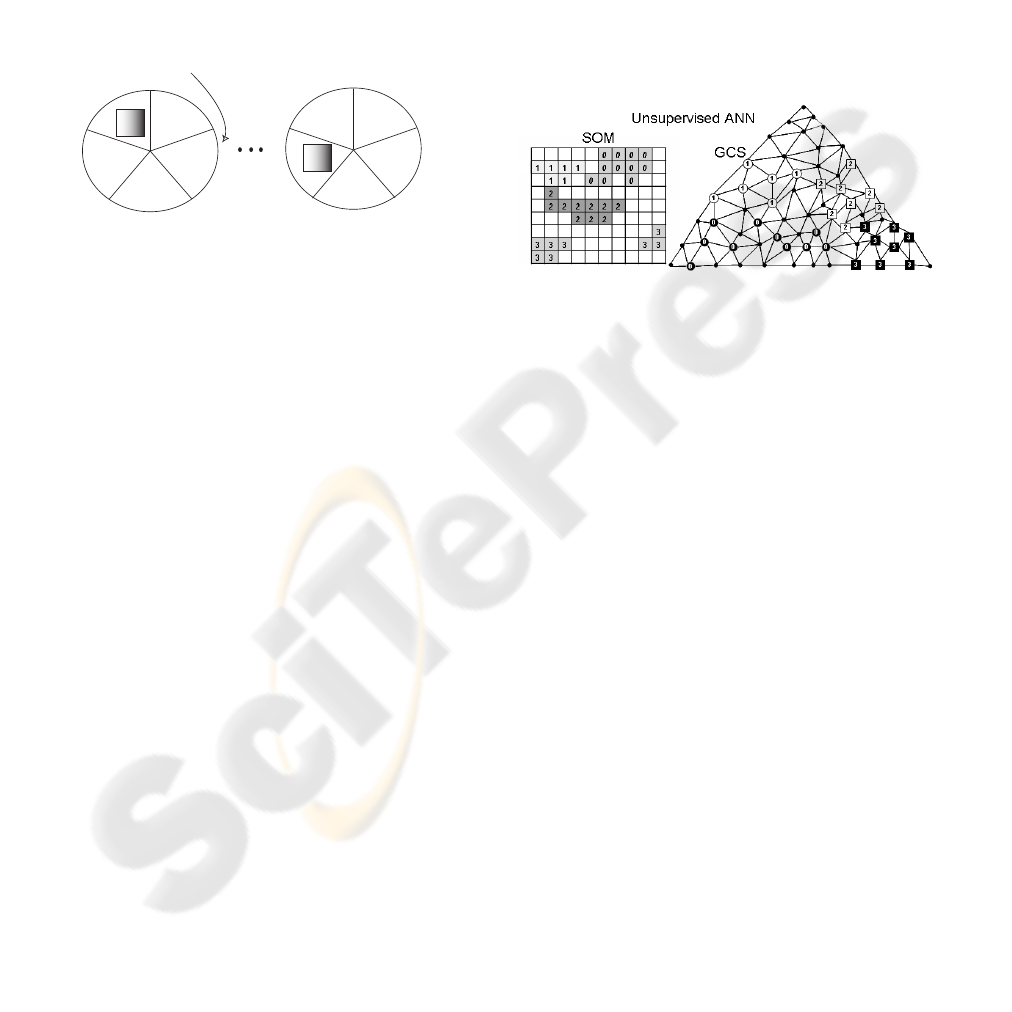
pervised ANNs give a useful visual information. This

is the reason why we believe a hybrid system with

supervised and unsupervised ANNs works properly

incorporating the advantages of each ANN.

This comparativeand its results with the three dif-

ferent types of ANNs not only has the goal of discov-

ering which is the best neural network but also and

mainly to ﬁnd out relations between the dysfunctions

(output of the network). As shown in ﬁgure 4 it will

help the urologist to pay attention in some tests and

its measures to increase the accuracy of the system.

In this regard, it will be possible to eliminate some of

the tests in order to save money, time and sometimes

pain for the patients.

To measure the performance of the ANNs we pro-

ceed as follow: Once the ANNs have been trained

there are some membership functions for each area,

we take a test and we see in which area it is cate-

gorized. If the neuron has only input vectors of the

same dysfunction the accuracy is 100% otherwise it

depends on the mix of dysfunctions and it is another

percentage (it incorporates the fuzzy logic idea since

it measures the degree of membership to the catego-

rized area). Moreover, a big advantage of using unsu-

pervised ANNs , as we can see in ﬁgure 4, is the visual

perception of the proximities of the different dysfunc-

tions (their membership functions) categorized in ar-

eas to ﬁnd out relations between similar inputs. The

system does not produce negative false. This fact

makes it highly reliable amongst the urologists.

Figure 4: Evaluation of the unsupervised ANNs.

4 CONCLUSIONS AND FUTURE

WORK

In this paper we have evaluated the performance of

three different kinds of artiﬁcial neural networks,

the Kohonen Self-Organizing Map, the Growing Cell

Structures and the Multilayer Perceptron with the

backpropagation algorithm, when applied to the cat-

egorization of urological dysfunctions. The ANNs

were trained with data from a database with registers

of different patients with urological dysfunctions.

The experiment starts with a stage of discretiza-

tion of the urodynamical measures from a patient in

order to provide them to the ANN and to determine

if there are any of the three dysfunctions of the LUT

or not. In case of ﬁnding a dysfunction it would de-

termine what type of dysfunction or dysfunctions the

patient could have.

The human expert is able to generalize by using

his experience. This big advantage is compensated for

ANNs by using graphs offering a visual perception.

The frontiers between two dysfunctions help the urol-

ogist to discover resemblances. They can also help

detecting similarities between ﬁelds or urodynamical

samples.

In this work we obtained comments valuable from

the urologists after using the system. They remarked

its advantages to give a more precise diagnosis and,

therefore, to save time and money to the public health.

Their comments encourage us to continue our work to

develop a system that uses the diagnosis obtained as

a result of the combined use of different neural net-

works. This gives an even more accurate diagnosis.

Next step is the use of data mining involving

several steps such as pre-processing with sampling,

cleaning and others learning methods as bayesian net-

works, decision trees, etc.

ACKNOWLEDGEMENTS

We want to express our acknowledgement to

Christian Balkenius for helpful comments on the

manuscript. The data used in the development of this

system is the result of several years of collaboration

with urologists of the Hospital of San Juan (Alicante-

Spain). The work has been supported by the Ofﬁce of

Science and Technology as part of the research project

“Cooperative diagnosis systems for Urological dys-

functions (2005-2006)”.

REFERENCES

Abrams, P. Urodynamics. 3rd edn., Springer, 2005,20-39.

Begg, R., Kamruzzaman, J., Sarkar R.: Neural Networks in

Healthcare: Potential and Challenges, 2006.

E.H. Shortliffe, Computer-Based Medical Consultations:

MYCIN, Elsevier/North Holland, New York, 1976.

Green, M., Bjork, J., Forberg, J., Ekelund, U., Edenbrandt,

L. and Ohlsson, M.: Comparison between neural net-

works and multiple logistic regression to predict acute

coronary syndrome in the emergency room. Artiﬁcial

Intelligence in Medicine, Vol. 38, (2006) 305-318.

Peled, A.: Plasticity imbalance in mental disorders the neu-

roscience of psychiatry: Implications for diagnosis

and research. Medical Hypotheses, Vol. 65, (2005)

947-952.

Politi, E., Balduzzi, C., Bussi, R. and Bellodi, L. Artiﬁcial

neural networks: a study in clinical psychopharmacol-

ogy, Psychiatry Research, Vol. 87, (1999) 203-215.

Suzuki, K., Shiraishi, J., Abe, H. MacMahon, H. and Doi,

K.: False-positive reduction in computer-aided diag-

nostic scheme for detecting nodules in chest radio-

graphs by means of massive training artiﬁcial neural

network. Academic Radiology, Vol. 12, (2005) 191-

201.

Remzi M., Djavan B., Seitz C., Hruby S., Marberger M.:

Artiﬁcial Neural Networks to predict the outcome of

repeat prostate biopsies. J Urol (2001).

Batuello JT., Gamito EJ, Crawford ED., Han M., Partin

AW., McLeod DG., et al.: Artiﬁcial Neural Network

Model for the assessment of lymph node spread in pa-

tients with clinically localized prostate cancer. Urol-

ogy, Vol. 57, (2001) 481–485.

Remzi M., Djavan B.: Artiﬁcial neural networks in urology.

European Urology, (2004) 33-38.

Gil, D., Soriano, A., Ruiz, D., Montejo, C.A.: Develop-

ment of an artiﬁcial neural network for helping to di-

agnose diseases in urology. Proceedings of the Bio-

Inspired mOdels of NEtwork, Information and Com-

puting Systems (BIONETICS’06), (2006).

Gil, D., Soriano, A., Ruiz, D., Garc´ıa, J., Fl´orez, F.; Deci-

sion support system for diagnosing dysfunctions inthe

lower urinary tract. 3rd European Medical and Biolog-

ical Engineering Conference. IFMBE European Con-

ference on Biomedical Engineering. (2005).

Ruiz, D., Garc´ıa, J.M., Mac´ıa, F., Soriano, A.: Robust Mod-

elling of Biological Neuroregulators. IEEE Engineer-

ing in Medicine and Biology Society, (2005).

Jiang, Y., Zheng, J., Peng, C. and Li, Q.: A multilayer

perceptron-based medical decision support system for

heart disease diagnosis. Elsevier, Expert Systems with

Applications, Vol. 30, (2006) 272-281.

Kohonen, T.: Self-Organization and Associative Memory,

Berlin Heidelberg, Springer-Verlag, (1988).

Kohonen, T.: The self-organizing map. Proceedings of the

IEEE, 78, 9, (1990) 1464-1480.

Kohonen, T.: Self-Organizing Maps, Berlin Heidelberg,

Springer-Verlag, (2001).

Fritzke, B.: Growing Cell Structures - A Self-organizing

Network for Unsupervised and Supervised Learning,

(1993) 93-126.

Fritzke, B.: Unsupervised ontogenic networks. In Fiesler

and Beale (eds.). Handbook of Neural Computation,

IOP Publishing Ltd. and Oxford University Press,

(1997).