HEALTHCARE RISK MODELING FOR MEDICAID PATIENTS

The Impact of Sampling on the Prediction of High-Cost Patients

Sai T. Moturu, Huan Liu

Department of Computer Science and Engineering, School of Computing and Informatics

Arizona State University, Tempe, AZ 85287

William G. Johnson

Center for Health Information & Research (CHiR), School of Biomedical Informatics

Arizona State University, Tempe, AZ 85287

Keywords: Predictive risk modeling, healthcare costs, high-cost patients, high-risk patients, non-random sampling,

over-sampling, under-sampling, imbalanced data, skewed data, Medicaid, data mining, classification.

Abstract: Healthcare data from the Arizona Health Care Cost Containment System, Arizona’s Medicaid program

provides a unique opportunity to exploit state-of-the-art data processing and analysis algorithms to mine

data and provide actionable findings that can aid cost containment. Our work addresses specific challenges

in this real-life healthcare application to build predictive risk models for forecasting future high-cost

patients. We survey the literature and propose novel data mining approaches customized for this compelling

application with specific focus on non-random sampling. Our empirical study indicates that the proposed

approach is highly effective and can benefit further research on cost containment in the healthcare industry.

1 INTRODUCTION

The Center for Health Information and Research

(CHiR) at Arizona State University houses a

community health data system called Arizona

HealthQuery (AZHQ). AZHQ contains

comprehensive health records of patients from the

state of Arizona linked across systems and time. The

data, which include more than six million persons,

offer the opportunity for research that can impact on

the health of the community by delivering actionable

results for healthcare researchers and policy makers.

One of the primary issues plaguing the

healthcare system is the problem of rapidly rising

costs. Many reasons have been put forward for the

consistent growth in health care expenditures

ranging from the lack of a free market and the

development of innovative technologies to external

factors like economy and population growth

(Bodenheimer, 2005). A first step to tackle these

issues is to devise effective cost containment

measures. One efficient approach to cost

containment is to focus on high-cost patients

responsible for these expenditures and undertake

measures to reduce these costs. Predictive risk

modeling is a relatively recent attempt at proactively

identifying prospective high-cost patients to reduce

costs. We embark on the challenging task of

building predictive risk models using real-life data

from the Arizona Health Care Cost Containment

System (AHCCCS), Arizona’s Medicaid program,

available in AZHQ. The AHCCCS data was selected

because it contains a large number of patients who

can be tracked over multiple years and it contains

many features needed for the analysis in this study.

Apart from data analysis challenges due to the

voluminous amount of patient records and the

considerable amount of variation for similarly

grouped patients, such cost data provides a bigger

challenge. It has been commonly observed that a

small proportion of the patients are responsible for a

large share of the total healthcare expenditures. This

skewed pattern has remained constant over many

decades. Previous studies show that more than two-

thirds of the health costs are from the top ten percent

of the population (Berk & Monheit, 2001). Similar

patterns are observed in our empirical study.

126

T. Moturu S., Liu H. and G. Johnson W. (2008).

HEALTHCARE RISK MODELING FOR MEDICAID PATIENTS - The Impact of Sampling on the Prediction of High-Cost Patients.

In Proceedings of the First International Conference on Health Informatics, pages 126-133

 SciTePress

Since a tiny percentage of patients create a large

portion of the impact, identifying these patients

beforehand would allow for designing better cost

containment measures. Early identification could

help design targeted interventions for these higher

risk patients who could then be part of more

effective, specially designed disease or case

management programs. Early identification could

help defer or mitigate extremely negative outcomes.

This approach also ensures that the different

players shaping the healthcare market be satisfied.

Insurers and employers who pay for the healthcare

costs would stand to gain considerably from reduced

costs. Employers in particular have an added

incentive as this would reduce other “indirect costs”

incurred due to the time taken by the patient to

return to work and the resulting loss of productivity.

Additional benefits for these players include better

return on investment due to an improvement in the

allocation of available resources and a basis for the

establishment of capitation reimbursements. On the

other hand, such an approach does not directly

impact providers and suppliers who provide services

to the patients. However, before achieving such

gains, the imbalanced nature of the data provides a

considerable challenge for accurate prediction.

As a part of this study, we propose a predictive

risk modeling approach to identify high-risk

patients. We use data mining and machine learning

techniques to design such an approach as they are

known to work well with large data and in particular

when the data collection has been automated and

performance takes precedence over interpretability

(Scheffer, 2002). Data mining has been successfully

used in the past for financial applications like credit

card fraud detection, stock market prediction, and

bankruptcy prediction (Zhang and Zhou, 2004).

Healthcare data provides a unique opportunity

for knowledge discovery using data mining while

also presenting considerable challenges. Despite the

success of data mining in various areas, it hasn’t

been regularly used to tackle these challenges

though limited examples exist (Anderson,

Balkrishnan, & Camacho, 2004; Cios & Moore,

2002; Li et al., 2005). We study the possibility of

applying data mining techniques to aid in healthcare

risk modeling, where we aim to forecast whether a

patient would be of high cost for the next year based

on data from the current year.

2 RELATED WORK

2.1 Learning from Imbalanced Data

Due to the existence of high-risk, high-cost patients

healthcare expenditure data is highly skewed. As a

result, it is essential to pay attention to the data

imbalance when dealing with such data. This is not

uncommon and has been observed in applications

like credit card fraud detection, network intrusion

detection, insurance risk management, text

classification, and medical diagnosis. The problems

of dealing with imbalanced data for classification

have been widely studied by the data mining and

machine learning community (Chawla, Japkowicz,

& Kolcz, 2004). Most classification algorithms

assume that the class distribution in the data is

uniform. Since the metric of classification accuracy

is based on this assumption, the algorithms often try

to improve this faulty metric while learning.

The two most common solutions to this problem

include non-random sampling (under-sampling or

down-sampling, over-sampling or up-sampling and a

combination of both) and cost-sensitive learning.

Both solutions have a few drawbacks (most

importantly, under-sampling might neglect few key

instances while over-sampling might cause

overfitting) but they have shown improvement over

conventional techniques (McCarthy, Zabar, &

Weiss, 2005; Weiss & Provost, 2001).

Various studies have compared over-sampling,

under-sampling and cost-sensitive learning. While

some found that there was little difference in the

results from these methods, others found one among

them to be the best. Results from different studies

are inconclusive in selecting the best among them

(Batista, Prati, & Monard, 2004; Drummond &

Holte, 2003; Maloof, 2003; McCarthy et al., 2005).

The use of a combination of under-sampling and

over-sampling has also been found to provide

improved results over the individual use of these

techniques. Additionally, it has be found using

varying ratios of the minority and majority classes

that the best results were generally obtained when

the minority class was overrepresented in the

training data (Estabrooks, Jo, & Japkowicz, 2004;

Weiss & Provost, 2001). The use of synthetically

generated instances for the minority class has also

been proposed (Chawla, Bowyer, Hall, &

Kegelmeyer, 2002) but the prudence of using this

technique for highly varied instances in healthcare

data needs to be evaluated.

Despite the reported success of these techniques

in other domains, none have been applied with

HEALTHCARE RISK MODELING FOR MEDICAID PATIENTS - The Impact of Sampling on the Prediction of

High-Cost Patients

127

respect to healthcare expenditure data in the past. In

this study, we explore the possibility of using non-

random sampling as a key element in creating

predictive models for identifying high-risk patients.

Preliminary work has confirmed the usefulness of

this approach (Moturu et al., 2007).

2.2 Techniques and Predictors

Healthcare data sets have been used in the past to

predict future healthcare utilization of patients where

the goal varied from being able to predict individual

expenditures to the prediction of total healthcare

expenditures. Typically, various regression

techniques have been employed in the past with

varying success for these tasks but the assumptions

of independence, normality and homoscedasticity

are not satisfied by the skewed distribution of the

costs. Regression techniques generally tend to

predict the average cost for a group of patients

satisfactorily but on an individual basis, the

predictions aren’t too accurate. Other approaches

include the transformation of the distribution to

match the assumptions of the analysis technique and

the use of the Cox proportional hazards model

(Diehr, Yanez, Ash, Hornbrook, & Lin, 1999).

Apart from these statistical methods, multiple

risk-adjustment models that can forecast individual

annual healthcare expenses are currently available.

These can be used to predict high-cost patients by

setting a cost threshold. Popular models including

Adjusted Clinical Groups (ACG), Diagnostic Cost

Groups (DCG), Global Risk-Adjustment Model

(GRAM), RxRisk, and Prior Expense show

comparable performance (Meenan et al., 2003).

The performance of predictive modeling

techniques is highly dependent on the data and

features used. Different sources have provided data

for the prediction of future utilization. Self-reported

health status information gathered from patients

using surveys has been used to predict medical

expenditures (Fleishman, Cohen, Manning, &

Kosinski, 2006) and group patients into cost

categories (Anderson et al., 2004). Unlike these

studies, our work employs administrative claims-

based data. For such data both demographic and

disease-related features have proven to be useful in

the past. Demographic variables like age have been

known to work well as predictors for expenditure.

Disease-related information in the form of

comorbidity indices has been used in the past as

predictors of healthcare costs and the use of both

inpatient and outpatient information was found to be

useful (Perkins et al., 2004). However, simple count

measures like number of prescriptions and number

of claims were found to be better predictors of

healthcare costs than comorbidity indices (Farley,

Harrdley, & Devine, 2006). Though the performance

of comorbidity indices might vary, disease-related

information is still a key predictor. Such information

from various utilization classes such as inpatient,

outpatient and pharmacy information has been used

in the past, either separately or together to predict

cost outcomes. Combining information from

different utilization classes has been found to be

useful (Zhao et al., 2005). In this study we use a set

of features similar to those that have proven useful

in the past together with data mining techniques that

haven’t been explored with respect to this area.

3 PREDICTIVE RISK

MODELING

3.1 Data and Features

The substantially large amount of data in AZHQ

necessitates the selection of a specific subset for

analysis. The requirement for a multi-year claims-

based data set representing patients of varied

demographics and containing disease-related

information from various utilization classes,

AHCCCS data is well-suited for risk modeling.

Despite being only a small part of AZHQ, AHCCCS

data provides a large sample size of 139039 patients.

2002

FEATURES

Demographic

Disease-related

2003

TURES

Demographic

Disease-related

2004

FEATURES

Demographic

Disease-related

Trainin

Testin

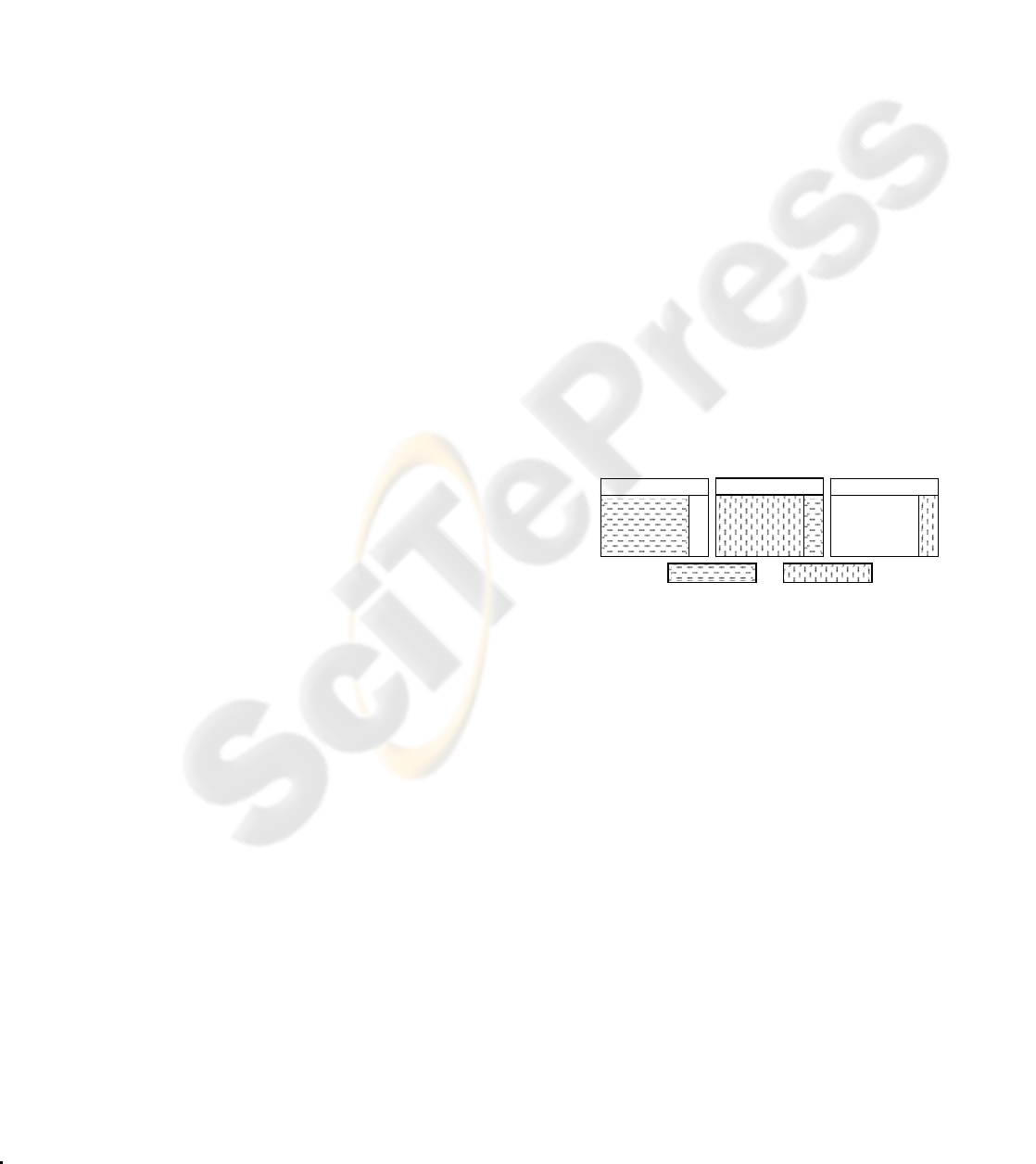
Figure 1: Illustration of Training and

Test Data Sets

Four hundred and thirty seven demographic and

disease-related features, either categorical or binary,

were extracted from the original AHCCCS data. The

patients were categorized into the minority or rare

class (high-cost) and the majority class based on the

paid amount. Figure 1 depicts the structure of the

data and its division into training and test data. Since

the goal is to predict future healthcare costs, features

from one year and class from the following year

have been used together. Training data was

constructed with features from 2002 and class from

2003 while test data was constructed with features

from 2003 and class from 2004.

Figure 1: Ilustration of Training and Test Data Sets.

HEALTHINF 2008 - International Conference on Health Informatics

128

The demographic variables employed include

age category (ages in groups of five), gender, race

(Asian, Black, Hispanic, Native American, White

and Other), marital status (single, married, divorced,

separated and widowed) and county. Age and gender

have been included due to previous success while

race, location and marital status have been added as

they could impact both financial and health aspects.

We avoid comorbidity or multimorbidity indices

due to lack of flexibility. To allow the inclusion of

inpatient, outpatient and emergency department

information, International Classification of Diseases

(ICD) procedure codes have been further grouped

into twenty major diagnostic categories (MDC). For

pharmacy data, the classification has been derived

from the National Drug Code (NDC) classification

with 136 categories. The practice of discounting

billed charges in the healthcare industry requires that

the amounts paid for the services are used as

measures of costs rather than the amounts charged.

Payments are used in this study and we select two

different thresholds for the separation of high-cost

patients. These thresholds of $50,000 (954 or 0.69 %

high-cost patients) and $25,000 (3028 or 2.18%

high-cost patients) ensure that the resultant data is

sufficiently highly skewed.

3.2 Analysis

Knowledge discovery using data mining requires

clear understanding of the problem domain and the

nuances of the data. These are achieved in the

previous sections. Further, the analysis consists of

three major steps. The first step is data preprocessing

and is considered one of the most important parts of

data mining. This is followed by the application of

data mining techniques on training data to learn an

appropriate model. Finally, this model is evaluated

on test data using suitable evaluation metrics.

Training and test data are created in the data

preprocessing step with required features being

extracted from the data. The creation of a training

data set provides a major challenge. The large size

of the data makes the learning task tedious and

necessitates the sampling of instances to reduce size.

The nature of imbalanced data sets, which invariably

result in poor performance while using conventional

analysis techniques, needs to be taken into

consideration for the selection of appropriate

training instances. To address this challenge, non-

random sampling has been employed as a

combination of over-sampling the minority class and

under-sampling the majority class to create a

training sample. This approach is reasonable as it

has been employed successfully with such data in

the past. Though the use of an equal number of

training instances from both classes seems intuitive,

it has been suggested that a higher number of

instances from the minority class might improve

sensitivity (Weiss & Provost, 2001). We evaluate

this suggestion using multiple training samples with

varying proportions of the two classes.

The next step is the creation of predictive

models. We have preliminarily tested a variety of

popular classification algorithms to focus on the

challenge of learning from the training data. Out of

the algorithms tested, five have worked considerably

better. These include AdaBoost (with 250 iterations

of a Decision Stump classifier), LogitBoost (also

with 250 iterations of a Decision Stump classifier),

Logistic Regression, Logistic Model Trees, and the

Support Vector Machine (SVM) classifier.

Performance evaluation provides the final

challenge in our analysis. Since the data is highly

skewed, traditional measures like accuracy aren’t

particularly useful. We propose the following four

evaluation metrics to gauge performance:

• Sensitivity: Sensitivity corresponds to the

proportion of correctly predicted instances of

the minority class with respect to all such

instances of that class. It is equal to the number

of true positives over the sum of true positives

and false negatives.

FNTP

• Specificity: Specificity corresponds to the

proportion of correctly predicted instances of

the majority class with respect to all such

instances of that class. It is equal to the number

of true negatives over the sum of true negative

and false positives.

FPTN

• F-measure: F-measure is typically used as a

single performance measure that combines

precision and recall and is defined as the

harmonic mean of the two. Here we use it as a

combination of sensitivity and specificity.

**2

•

G-mean: G-mean typically refers to geometric

mean and in this study it is the geometric mean

of sensitivity and specificity.

PTM SSG *=

HEALTHCARE RISK MODELING FOR MEDICAID PATIENTS - The Impact of Sampling on the Prediction of

High-Cost Patients

129

To evaluate the performance of predictive risk

models, it is necessary to understand the relevance

of their predictions. The identification of high-cost

patients allows for targeted interventions and better

case management. Therefore, identifying most of

these patients would prove useful. Such high

sensitivity is achieved with a corresponding decrease

in specificity, which is acceptable due to the cost

benefits from identifying a large percentage of the

high-cost patients. Consider the following example

of two predictive models created using non-random

and random sampling whose predictions are

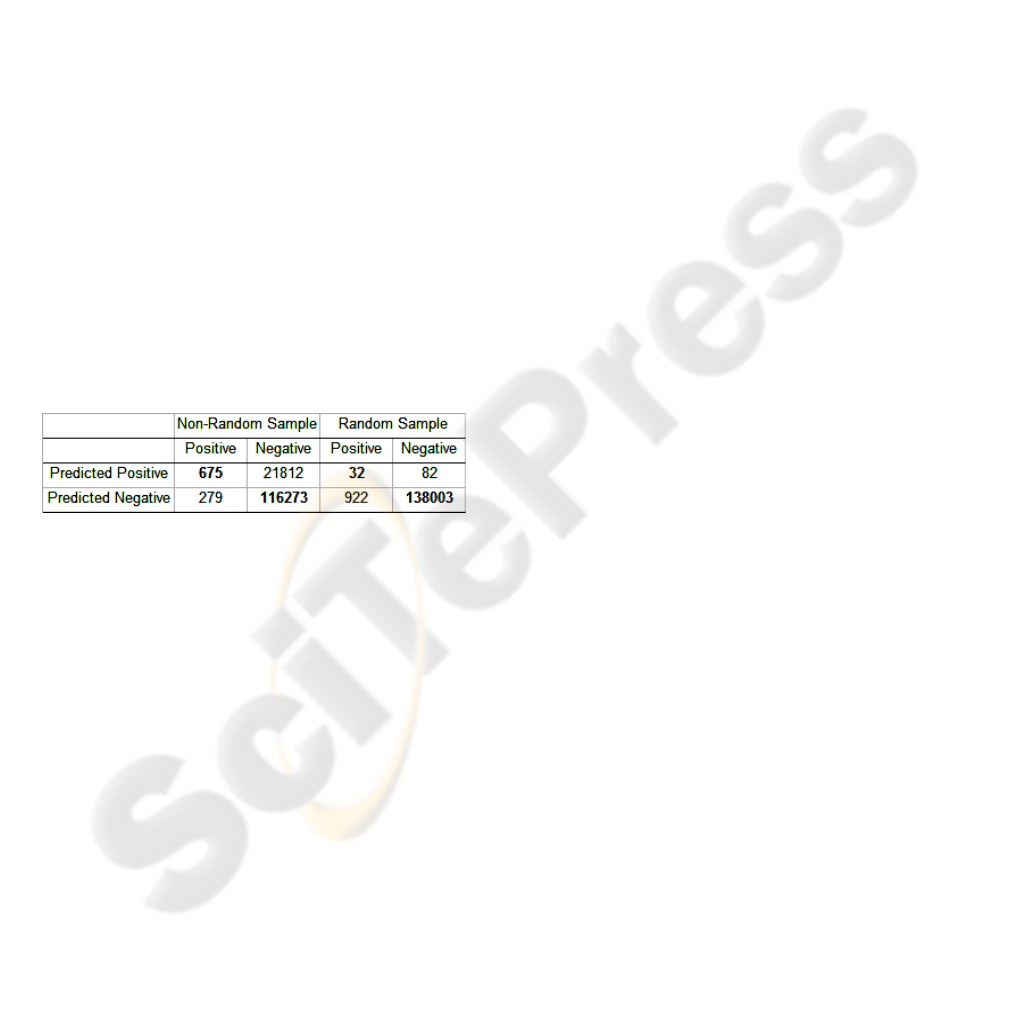
depicted through a confusion matrix in table 1.

Identifying a limited number of high-cost patients

(32 as opposed to 675) with greater prediction

accuracy means that a large percentage of high-cost

patients are unidentified and therefore a considerable

portion of the health and cost benefits are

unattainable. Alternatively holding targeted

interventions and providing effective disease

management for 22487 patients (675 correct and

21812 incorrect) could result in health benefits for

the actual high-risk patients and cost benefits for the

employers and insurers. This example indicates the

need for high sensitivity along with an acceptable

trade-off between specificity and sensitivity.

Table 1: Random vs. Non-random Sampling.

3.3 Predictive Modeling

Recall that our preliminary results indicate the

usefulness of non-random sampling for predictive

modeling. Further, we identified five classification

algorithms that show promise and delineated four

measures for performance evaluation considering the

imbalance of data. These elements set the stage for

an empirical study designed to markedly indicate the

usefulness of non-random sampling to our approach

for predictive modeling. Further, this sampling

technique is applied on suitably varied training data

samples. Additionally, two class thresholds are used

to check for the robustness of our approach to

differently skewed data sets. These experiments help

to provide a comparative outlook of our approach

and also indicate its benefits and flexibility.

4 EMPIRICAL STUDY

We first provide details of our experimental design

along with the software environment, algorithms and

then discuss experimental results.

4.1 Experimental Design

Employing the AHCCCS data as depicted in Section

3.1, we evaluate the predictions across an extensive

range of experiments. All experiments have been

performed using the Weka software (Witten &

Frank, 2005). Training data is created from the data

set with features from 2002 and class from 2003.

The model learned from this training data is used to

predict on the test data set with features from 2003

and class from 2004. Non-random sampling was

used to create training data as a default. The default

class threshold used was $50,000. For each

experiment, the five algorithms listed previously

have been used to create predictive models with a

goal of identifying the best one. The following

dimensions were used for comparison.

4.1.1 Random Versus Non-Random

Sampling

Experiments across this dimension were designed to

depict the differences in performance between the

sampling techniques. One set of experiments used

random sampling where 50% of the data was

randomly selected for training. Another set of

experiments used non-random sampling where the

minority class was over-sampled and the majority

class was under-sampled. Twenty different random

samples were obtained for both classes, with every

sample containing 1,000 instances. The resulting

training data sample contained 40,000 instances.

4.1.2 Varying Proportions of the Minority

Class Instances in the Training Data

These experiments were designed to evaluate the

differences of learning using non-randomly sampled

data with varied proportions of rare class instances.

Multiple training data sets were created with

proportions of instances from the minority class

being 10%, 25%, 40%, 60%, 75% and 90%.

Random samples of 1000 instances each were drawn

both classes according to the appropriate proportion

for that training data set. However, the total number

of instances was maintained at 40,000. For example,

the training set with 40% rare class instances had 16

random samples from that class resulting in 16,000

instances. Six different non-randomly sampled

HEALTHINF 2008 - International Conference on Health Informatics

130

training data sets were obtained in addition to the

existing one with equal instances from both classes.

4.1.3 Varying the Class Threshold

Two different thresholds ($50,000 and $25,000) for

the differentiation of high-cost patients have been

used for the various training data samples described

in Section 4.1.2 to assess whether our approach is

robust to variations along this boundary.

4.2 Results and Discussion

4.2.1 Importance of Non-Random Sampling

Both random and non-random samples are drawn

from the same data set to form training data in order

to build predictive models. The purpose of this

experiment is twofold: (1) to verify whether non-

random sampling is indeed necessary as suggested in

our preliminary analysis, and (2) to use a baseline to

compare predictions from the two techniques. It is

apparent from Table 2 that random sampling

provides very poor sensitivity with less than ten

percent of the high-cost patients identified correctly.

We can also consider a baseline model where

patients are predicted to be in the same class as they

were in the previous year. Such a model performs

better with a sensitivity of 0.276 and a specificity of

0.993 for this data set resulting in an F-measure of

0.432 and a G-mean of 0.524. The low sensitivity

indicates that not many high-cost patients remain in

that category the following year making predictive

modeling more difficult. Non-random sampling

shows a marked improvement but as one would

expect, this comes with a loss in specificity.

Nevertheless, the F-measure and G-mean are much

higher indicating that the trade-off between

sensitivity and specificity is better than the baseline.

These results clearly indicate the effectiveness of

non-random sampling for predictive modeling.

4.2.2 Classification Algorithm Performance

Five different classification algorithms were used to

learn predictive models across the experiments with

the purpose of identifying the best among them.

Recall that these algorithms were selected over

many other algorithms based on our preliminary

analysis. Results from Table 2 (and similar

comparisons in Section 4.2.3 as shown in Figure 2)

clearly indicate that these five algorithms perform

consistently well with very similar sensitivity and

specificity making it difficult to select the best one.

One can only conclude that any of these algorithms

could be used to learn a suitable predictive model

from a non-randomly sampled training data set.

Combining results in Section 4.2.1, we conclude that

all classification models perform similarly poorly or

well with random or non-random sampling. Hence,

non-random sampling plays an instrumental role in

significantly boosting performance.

Table 2: Random vs. Non-random Sampling.

Table 3: Varying class proportions in training data.

4.2.3 Using Varied Class Proportions

Using a higher proportion of minority class instances

in the training data sample is expected to improve

results (Weiss & Provost, 2001). Experiments were

designed to evaluate this expectation and this trend

is observed with our data as well. Table 3 depicts the

results for this comparison using the LogitBoost

algorithm. Using a higher proportion of minority

class instances in the sample (60% and 75%)

performs better than an equal proportion as indicated

by both the F-measure and the G-mean. A receiver

operating characteristics (ROC) curve can be

generated from these different proportions. Figure 2

depicts such a curve that provides a better visual

representation of the improvement in results. It has

to be noted that the two cases with improved results

HEALTHCARE RISK MODELING FOR MEDICAID PATIENTS - The Impact of Sampling on the Prediction of

High-Cost Patients

131

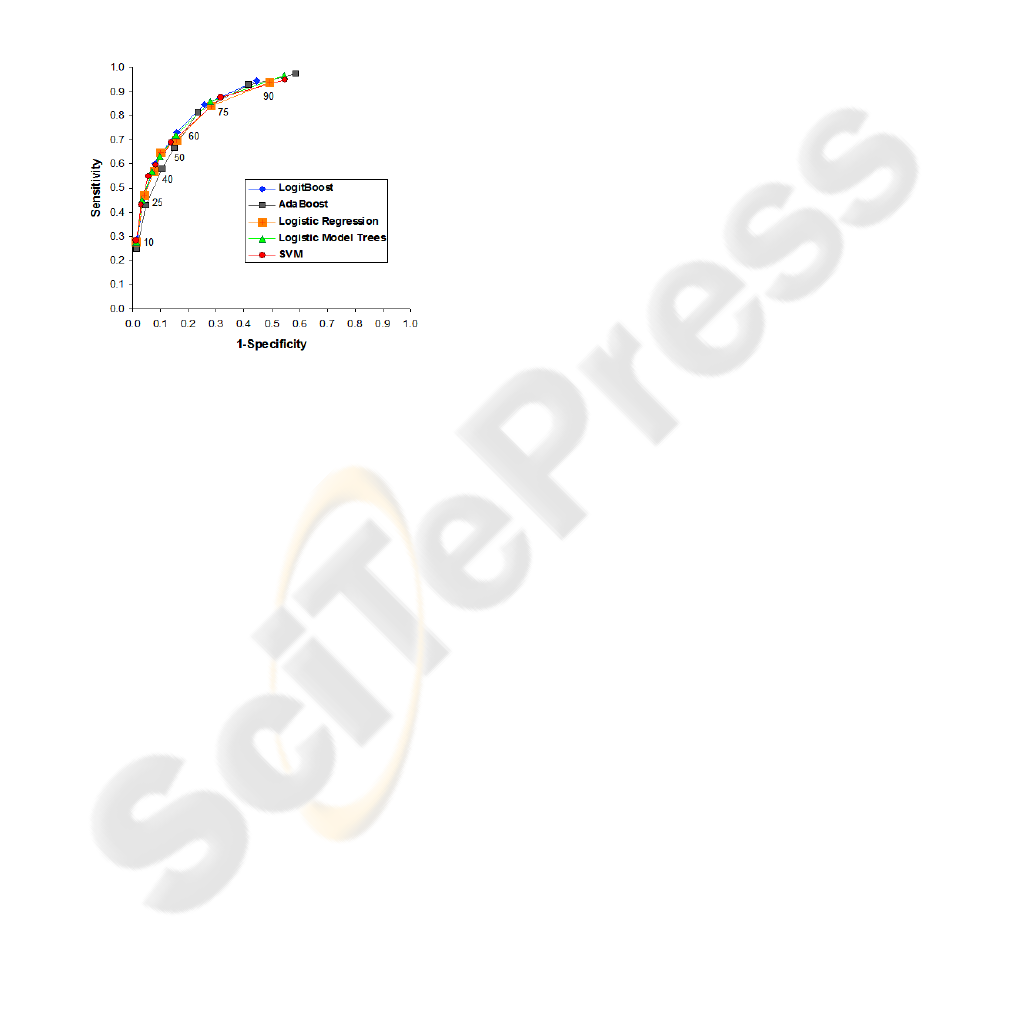
(60% and 75%) show a very different trade-off

between sensitivity and specificity despite similar

values for the F-measure and G-mean. Such an

observation indicates a unique opportunity to deal

with differences across the differently proportioned

samples. It is difficult to identify a suitable trade-off

without the availability of data that can establish the

cost benefits to be gained from a particular trade-off.

In such a scenario, such experiments can be

invaluable as they provide multiple trade-offs to

choose from. Upon the availability of information

about the cost benefits, the suitably proportioned

training data sample can be selected for analysis.

Figure 2: ROC Curve.

4.2.4 Varying the Class Threshold

Two thresholds for the differentiation of cost

categories have been used to indicate the robustness

of our approach to changes in class threshold. We

observe from Table 3 that results for both the

thresholds are comparable with the higher threshold

proving slightly better as indicated by F-measure

and G-mean. Since the training data is balanced by

non-random sampling, the slight underperformance

from the data with lower threshold could be due to

the fact that there are more patients closer to the

lower threshold, increasing the chance of an error in

prediction. This particular comparison serves to

indicate the adaptability of our approach while using

differently skewed data sets for predictive modeling.

5 CONCLUSIONS

Predictive risk modeling for forecasting high-cost

patients is an important area of research and this

study provides a look at a beneficial new technique

using a real-world data set. Results indicate that

creating training data using non-random sampling

helps balance the challenges resulting from the

skewed nature of healthcare cost data sets. Further,

over-representing the minority class in the training

data helps improve performance. Our study

manifests the significance of sampling in building

predictive risk models. However, it is hard to judge

the best trade-off between specificity and sensitivity

when there is no available data on the cost benefits.

In this sense, using varied proportions of instances

from the two classes in the training data can work as

a boon in disguise. When data on cost benefits is

available, one can test the use of different

proportions of instances from the two classes to

select the case with the best cost benefit. This makes

our approach for predictive modeling much more

adaptable.

Our comparison of classification algorithms for

this task indicates that all of the selected ones work

almost equally well. Though we find that it is hard to

choose between these algorithms, results indicate to

future users a handful of appropriate classification

techniques to be used along with non-random

sampling for predictive modeling. Our proposed

approach creates a model by learning from the data

and is therefore not restricted to the use of a specific

type of data or features. Further, the threshold for

high-cost patients is tunable and can be varied

depending on the goals of a particular study. All

these taken together signify the flexibility of

predictive risk modeling for future high-cost patients

using classification techniques to learn from non-

randomly sampled training data and the benefits that

can be obtained from such analyses.

Considering the variation in data, predictors

and evaluation metrics, comparison with previous

studies is improper, Nevertheless, the ROC curve in

Figure 2 is similar (the performance of the best

model is comparable) to that obtained for existing

risk-adjustment models (Meenan et al., 2003). The

numbers are also better (our results double the

sensitivity at about the same level of specificity)

than a decision-tree based predictive modeling

technique (Anderson et al., 2005). This validates the

usefulness of this technique that is further enhanced

by its flexibility. As can be observed, sampling is the

most important component of this technique and is

very beneficial for predictive modeling

Predictive risk modeling is a useful technique

with practical application for numerous employers

and insurers in the goal to contain costs. We provide

a promising approach that is valuable, flexible and

proven to be successful on real-world data.

Nevertheless, there is further scope to improve the

interpretation of these results. It is commonly

observed that a considerable percentage of high-cost

HEALTHINF 2008 - International Conference on Health Informatics

132

patients do not remain that way every year. Also,

two patients could share very similar profiles with

only one of them being high-cost. Studying these

seemingly anomalous patients could provide a better

understanding of how a high-cost patient is different

from other patients. In addition, the current sampling

approach and available classification techniques

could be further tuned to improve results.

Apart from these possibilities, the most

promising future direction is in working with key

data partners. This avenue provides the opportunity

to obtain information on the cost containment

methods used and their efficiency as well as real

data on the cost benefits obtained from previous

predictive models. Working with such partners, we

endeavor to provide a reasonable, patient-specific

answer to this question that would significantly

impact cost containment in the healthcare industry.

REFERENCES

Anderson, R.T., Balkrishnan, R., & Camacho, F. (2004).

Risk Classification of Medicare HMO Enrollee Cost

Levels using a Decision-Tree Approach. Am J

Managed Care, 10(2), 89-98.

Batista, G. E. A. P. A., Prati, R. C., & Monard, M. C.

(2004). A Study of the Behavior of Several Methods

for Balancing Machine Learning Training Data. ACM

SIGKDD Explorations Newsletter, 6(1), 20-29.

Bodenheimer, T. (2005). High and Rising Health Care

Costs. Part 1: Seeking an Explanation. Ann Intern

Med, 142, 847-854.

Berk, M. L., & Monheit, A. C. (2001). The Concentration

of Health Care Expenditures, Revisited. Health

Affairs, 20 (2), 9-18.

Chawla, N. V., Bowyer, K. W., Hall, L. O., &

Kegelmeyer, W. P. (2002). SMOTE: Synthetic

Minority Over-sampling Technique. Journal of

Artificial Intelligence Research, 16, 321-357.

Chawla, N. V., Japkowicz, N., & Kolcz, A. (2004).

Editorial: Special Issue on Learning from Imbalanced

Data Sets, ACM SIGKDD Explorations Newsletter,

6(1), 1-6.

Cios, K. J., & Moore, G. W. (2002). Uniqueness of

Medical Data Mining. Artificial Intelligence in

Medicine, 26(1-2), 1-24.

Diehr, P., Yanez, D., Ash, A., Hornbrook, M., & Lin, D.

Y. (1999). Methods For Analysing Health Care

Utilization and Costs. Ann Rev Public Health, 20, 125-

144.

Drummond, C., & Holte, R. C. (2003). C4.5, Class

Imbalance, and Cost Sensitivity: Why Under-

Sampling beats Over-Sampling. ICML Workshop

Learning From Imbalanced Datasets II, 2003.

Estabrooks, A., Jo, T., & Japkowicz, N. (2004). A

Multiple Resampling Method For Learning From

Imbalanced Data Sets. Computational Intelligence,

20(1), 18-36.

Farley, J. F., Harrdley, C. R., & Devine, J. W. (2006). A

Comparison of Comorbidity Measurements to Predict

Health care Expenditures. Am J Manag Care, 12, 110-

117.

Fleishman, J. A., Cohen, J. W., Manning, W.G., &

Kosinski, M. (2006). Using the SF-12 Health Status

Measure to Improve Predictions of Medical

Expenditures. Med Care, 44(5S), I-54-I-66.

Li, J., Fu, A. W., He, H., Chen, J., Jin, H., McAullay, D. et

al. (2005). Mining Risk Patterns in Medical Data. Proc

ACM SIGKDD Int’l Conf. Knowledge Discovery

in Data Mining (KDD’05), 770-775.

Maloof, M. (2003). Learning When Data Sets are

Imbalanced and When Costs are Unequal and

Unknown. ICML Workshop Learning From

Imbalanced Datasets II, 2003.

McCarthy, K., Zabar, B., & Weiss, G. Does cost-sensitive

learning beat sampling for classifying rare classes?

Proc 1

Int’l Workshop on Utility-based data mining

(UBDM ’05), 69-77.

Meenan, R. T., Goodman, M. J., Fishman, P. A.,

Hornbrook, M. C., O’Keeffe-Rosetti, M. C., &

Bachman, D. J. (2003). Using Risk-Adjustment

Models to Identify High-Cost Risks. Med Care,

41(11), 1301-1312.

Moturu, S.T., Johnson, W.G., & Liu, H. (2007). Predicting

Future High-Cost Patients: A Real-World Risk

Modeling Application. Proc IEEE International

Conference on Bioinformatics and Biomedicine 2007,

Accepted.

Perkins, A. J., Kroenke, K., Unutzer, J., Katon, W.,

Williams Jr., J. W., Hope, C. et al. (2004). Common

comorbidity scales were similar in their ability to

predict health care costs and mortality. J Clin

Epidemiology, 57, 1040-1048.

Scheffer, J. (2002). Data Mining in the Survey Setting:

Why do Children go off the Rails? Res. Lett. Inf.

Math. Sci., 3, 161-189.

Weiss, G.M., & Provost, F. (2001). The Effect of Class

Distribution on Classifier Learning: An Empirical

Study, (Dept. Computer Science, Rutgers University,

2001), tech report ML-TR-44.

Witten, I. H., & Frank, E. (2005). Data Mining: Practical

machine learning tools and techniques, 2nd Edition,

San Francisco: Morgan Kaufmann.

Zhang, D., & Zhou, L. (2004). Discovering Golden

Nuggets: Data Mining in Financial Application. IEEE

Trans. Sys. Man Cybernet., 34(4), 513-522.

Zhao, Y., Ash, A. S., Ellis, R. P., Ayanian, J. Z., Pope, G.

C., Bowen, B. et al. (2005). Predicting Pharmacy

Costs and Other Medical Costs Using Diagnoses and

Drug Claims. Med Care, 43(1), 34-43.

Zweifel, P., Felder, S., & Meiers, M. (1999). Ageing of

Population and Health Care Expenditure: A Red

Herring. Health Econ, 8, 485-496.

HEALTHCARE RISK MODELING FOR MEDICAID PATIENTS - The Impact of Sampling on the Prediction of

High-Cost Patients

133