A MECHATRONIC DEVICE FOR THE REHABILITATION OF

ANKLE MOTION

Giuseppe Bucca, Alberto Bezzolato, Stefano Bruni

Department of Mechanical Engineering, Politecnico di Milano, Via La Masa 34, Milano, Italy

Franco Molteni

Valduce Villa Beretta Rehabilitation Centre, Italy

Keywords: Mechatronics, gait analysis, biomechanic models.

Abstract: The paper presents the main results from a research aiming at the design of an electro-mechanical actuator

to assist walking movements of the ankle articulation, for use in the rehabilitation of lower limb motion in

patients suffering neurological disease. Motivations for the research project are discussed within the

framework of the application of mechatronic concepts within rehabilitation practice. The entire design

process is then described, from the definition of project target through the mechanical concept and control

design steps until design validation by means of numerical simulations and tests on a prototype.

1 INTRODUCTION

In recent years, mechatronics has emerged as a

powerful approach to provide innovative solutions in

many technical fields related with mechanical and

electronic engineering, and also in the field of

bioengineering. This paper presents an application of

mechatronic concepts to improve the effectiveness

of therapies addressing the rehabilitation of lower

limb motion in patients suffering neurological

disease.

The project is being developed as a joint

cooperation of the Politecnico di Milano (Technical

University of Milan) and the Villa Beretta rehabilita-

tion centre, part of Valduce Hospital, and is part of

HINT@Lecco, a large research program aiming at

the promotion of research fostering new applications

in the fields of medical diagnostics and therapy.

Aim of the project is to design an electro-

mechanical actuator to assist walking movements of

the ankle articulation, referred to as “ankle actuator”.

The system has been designed for use either as

integrated with the Lokomat rehabilitation device

(Colombo et Al, 2000) presently in use at Villa

Beretta, or as a standalone device to assist

physiotherapy.

In the paper, the need and possible applications of

the ankle actuator are described under the point of

view of rehabilitation practice (Section 2), then the

results of measurements and numerical simulations

based on biomechanic multi-body models are

reported, with the aim of setting the targets for the

project (Section 3). The mechatronic design of the

system and the identification of appropriate control

strategies to meet the targets of the project are

described in Sections 4 and 5. Finally, Section 6

reports about the final assessment of system

performances, that was pursued by a combination of

testing on a prototype demonstrator and multi-

physics simulation of the actuator fitted on a person,

involving the modelling of the lower limb and of the

actuator together with the control unit.

2 USE OF THE DEVICE FOR

REHABILITATION PURPOSES

The equinovarus foot is the most common

pathological lower limb posture after lesions that

result in an upper motor neuron syndrome (UMNS).

The lack of normal motor control and/or the

presence of static foot deformity alters the cyclical

kinematic pattern of lower limb and trunk during

gait. There may be impairment of advancement of

the body weight over the supporting limb and to

Bucca G., Bezzolato A., Bruni S. and Molteni F. (2008).

A MECHATRONIC DEVICE FOR THE REHABILITATION OF ANKLE MOTION.

In Proceedings of the First International Conference on Biomedical Electronics and Devices, pages 56-63

DOI: 10.5220/0001047500560063

 SciTePress

swing the unloaded limb forward in preparation for

the next step. Foot pain, skin breakdown (lateral

border, fifth metatarsal) and knee hyperextension

(and/or varus) are frequently associated to this gait

deviation and the compensation needed for the lack

of adequate base of support, limitation of ankle

dorsiflexion, dysrhytmic and restrained forward

translation of body mass, asymmetrical weight

transfer and interference with weight bearing on the

involved limb. Gait deviations and compensations in

the involved limb induce compensations for the non-

involved limb, pain and fatigue.

The equinovarus foot impairment is the result of

different combinations of the following

dysfunctions:

a) decrease of dorsiflexor muscles motor control

during swing phase;

b) increase activity of plantarflexor muscles;

c) reduction of the elastic properties of the calf

muscles.

The main goal of rehabilitation procedures is to

maintain ankle passive range of motion , to reduce

“learning non use” due to weakness of dorsiflexor

muscles, to maintain the elastic properties of

dorsiflexor/plantarflexor muscles.

3 TARGETS FOR THE PROJECT

A first step of the research consisted in defining

quantitative targets for the mechatronic ankle

actuator, in view of allowing the correct choice of

the actuation system and the proper mechanical

design of the system. This was done through a

combination of experiments to measure relevant

gait parameters and of gait mechanics modelling

and simulation by a biomechanical multi-body

model.

3.1 Measure of Gait Parameters

An experimental campaign was performed on

healthy subjects, with the aim of obtaining the

references corresponding to correct motion, to be

reproduced under the assistance of the mechatronic

ankle actuator. Lower limb movements were

measured by means of an ELITE opto-electronic

system for motion analysis, whereas contact forces

under the footprint were measured by means of

dynamometric platforms.

These measurements allowed to quantify the

required maximum speed, maximum force and

power targets for the ankle actuator. Furthermore, a

rather large set of measured data was made

available, allowing the validation of the bio-

mechanical multi-body model in view of its use in a

later stage of the project (see Section 6.1). Some of

the experimental results are shown in the next

paragraph, where they are compared with the results

of a simulation model. Despite it is known that in

case of patients with neurological diseases, muscle

configurations may present a different situation

compared to the healthy population, the aim of this

device is to reproduce a healthy subject gait on

patients with moderate neurological diseases.

Applications on subjects with more serious diseases

have to be verified by means experimental tests.

3.2 Numerical Simulations

A multi-body human model was defined in

ADAMS/LifeMOD environment, with the aim of

complementing measurements to define the targets

of the project. Moreover, the same model was used

in a later stage of the project, being interfaced with a

model of the ankle actuator, for performance

assessment purposes (see Section 6.1).

The model includes the pelvis and the two legs,

and was used to perform inverse and forward

dynamic simulations. In the target definition phase,

numerical simulations were used to evaluate gait

parameters that could not be directly measured, as

the ankle torque, and to derive gait parameters under

conditions that could not be tested.

The multi-body model was validated based on

comparison with the measurements described in

Section 3.1. As an example, Figure 1 shows the time

history of the measured and simulated vertical

contact force component for a healthy male person

weighting of 68kg and being 1,72m tall. Figure 2

shows the experimental vs. numerical comparison of

right foot marker position during gait on a treadmill,

for the same subject as in Fig. 1.

0 0.5 1 1.5 2

200

400

600

800

t[s]

[N]

Experimental results

1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8

200

400

600

800

t[s]

[N]

Simulation results

Left foot

Right foot

Left foot

Figure 1: Contact forces for a male person. Up:

experimental results; down: results of numerical

simulation.

A MECHATRONIC DEVICE FOR THE REHABILITATION OF ANKLE MOTION

0 200 400 600 800 1000

100

200

300

400

x[mm]

y[mm]

Experimental results

-200 0 200 400 600 800 1000

100

200

300

400

x[mm]

y[mm]

Simulation results

Figure 2: Right foot marker position for a male person: a)

experimental results; b) results of numerical simulation.

The comparison of measured vs. simulated results

allows to conclude that the mathematical model is

able to capture correctly the main issues of gait

mechanics and can be hence used to evaluate gait

parameters under conditions that cannot be

physically tested.

After validation, the model was used to derive

quantitative targets for the ankle actuator, taking into

consideration the effect of the Lokomat body weight

support (b.w.s) system. The kinematic targets, not

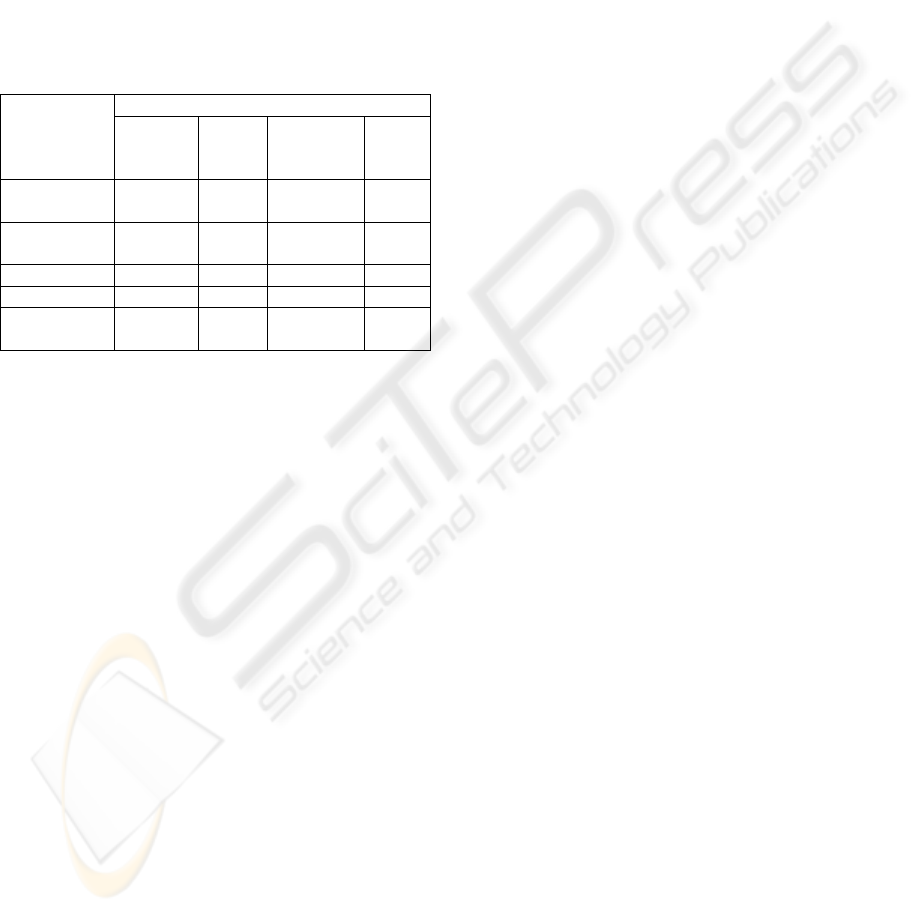
dependent upon the b.w.s. level, are listed in

Table 1, while torque and power requirements for

different levels of b.w.s. are compared in Table 2.

Table 1: Kinematic targets for the ankle actuator.

MIN MAX

Ankle rotation -10° 20°

Ankle velocity -200°/s 150°/s

Table 2: Torque and power targets corresponding to

different body weight support (b.w.s) levels.

MAX RMS

Torque 112 Nm 54.4 Nm

b.w.s 0%.

Power 152.6 W 48.6 W

Torque 81.6 Nm 43.6 Nm

b.w.s 25%

Power 125.9 W 41.5 W

Torque 65.1 Nm 31.2 Nm

b.w.s 50%

Power 90 W 29.3 W

Torque 31.8 Nm 15.6 Nm

b.w.s 75%

Power 53.8 W 14.5 W

Torque 24 Nm 8.37 Nm

b.w.s 90%

Power 34 W 7.36 W

Measurements described in a companion paper

(Bocciolone et Al., 2008) showed that the Lokomat

body weight support system provides a relief of at

least 85% of patient’s weight. Accordingly, torque

and power targets for the project were assumed in a

precautionary way to correspond to 75% body

weight support.

The target motion of the ankle articulation was

derived based on ELITE measurements (averaged to

remove the intrinsic variability of each step) and on

multi-body simulations. This was made considering

a healthy subject, since the target of the system is to

have the ankle performing a physiologically correct

motion. As an example, the reference time history of

ankle rotation for the same male subject considered

above and for a walking speed of 2km/h is presented

in Figure 3.

0 0.5 1 1.5 2

-5

t[s]

[°]

Reference motion law - ankle angle

Figure 3: Reference motion law (talo-crural joint) for a

male person.

4 THE CONCEPT

Besides the quantitative performance requirements

resumed in Section 3, a number of qualitative

requirements were defined for the ankle actuator, as

detailed below:

– high intrinsic safety;

– fast and simple installation on the patient’s leg

(wearability);

– low weight, small size and low visual impact;

– low emission of noise and heat;

Furthermore, in case the device is used on a

Lokomat machine, the mounting/dismounting of the

ankle actuator over the Lokomat exoskeleton should

not require any modification of the original

structure.

The concept phase was then divided in two stages:

selection of the type of actuator and design of the

interface with the patient.

As far as the choice of the actuator is concerned,

four alternatives were initially identified:

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

a) controlled electrical drive with rotating motor;

b) controlled electrical drive with linear motor;

c) controlled pneumatic actuator;

d) controlled Shape Memory Alloy (SMA)

actuator.

These solutions were thoroughly analysed and

compared evidencing for each advantages and weak

points in view of the specific application. The main

results of this comparison are summarized in Table

Table 3: Comparison among main possible solution for the

actuators of device.

Solution

Requirement

Rotating

motor

Linear

motor

Pneumatic

actuator

SMA

actuat

Max.

Torque

Good

Very

good

Very

good

Poor

Dynamical

response

Very

good

Very

good

Good Poor

Wearability Good Good Short Fair

Cost Good Fair Fair Fair

Weight and

dimensions

Very

good

Very

good

Poor Good

The electrical drive with a rotating motor (DC or AC

brushless) satisfies all main requirements: it has low

weight and appropriate dimensions, affordable cost

and simple structure which allows to build a device

with a good wearability. Finally, a quite wide variety

of solutions (in terms of size and specific features) is

available on the market, allowing to tailor the choice

in view of the requirements of the specific

application. The drawback of this solution is the

need of using an epicycloidal gear reducer, because

rotating motors present high speed and low torque,

while for ankle actuation, mechanical power is

needed in the form of a relatively high torque acting

at relatively low speed. The use of a gear reducer

implies an increase in the weight of the device,

which can be however kept within reasonable limits.

The linear motor mainly has the same advantages

of the rotating motor and does not bear the drawback

of using a gear reducer, because linear motors

provide relatively high force at low speed, but is

much more expensive than rotating motors, requires

a more complicate mechanical design of the system

and less alternatives are offered on the market.

Pneumatic actuation was considered also

referring to previous applications to ankle actuation:

(Sawicki, 2005) and (Ferris, 2005) showed that this

kind of actuation is able to reproduce with good

accuracy the features of actual ankle motion. In view

of the aims of this project however, this solution

compared to electromechanical solution provides

lower actuation speed, lower maximum control force

and requires auxiliary systems of relatively large

size and potentially disturbing, like the air

compressor.

The SMA actuator solution was also considered

based on some tentative applications in the bio-

medical field, including a parallel project within the

HINT research project. However, besides some

practical disadvantages like the need for a rather

complicated cooling system, present SMA actuation

technology appears to suffer from an insufficient

dynamical response which is not able to ensure the

required actuation speed to implement ankle motion

control.

Based on the analysis summarized above, the

solution based on rotating electric motor was

identified as the most appropriate in terms of

technical requirement and related costs and was

chosen for development. In particular, a 150 W DC

motor (MAXON RE40 150W), driven by a 4-Q-DC

servoamplifier (MAXON ADS 50/10) and coupled

with an epicycloidal gear reducer with a gear ratio of

1:113 (MAXON GP 52C) was chosen.

The second stage of the concept development

consisted in the design of the interface between the

actuator and the leg. The basic idea underlying this

activity was to implement a configuration similar to

the one used in the Lokomat machine. On that

device, the feet are restrained by a sling held by an

arm rigidly connected to the exoskeleton (Figure 4).

The concept for interfacing active ankle actuation

with the patient’s leg was then based on the idea of

replacing the passive arm with an articulated

mechanical system, properly connected with the

motor, so that ankle actuation may be obtained by an

appropriate movement of the final link in the

articulated system. The functional scheme of the

solution identified is reported in Figure 5a: a support

is fixed over the Lokomat exoskeleton, and

connected by a hinge with a link which is actuated

by a crank fitted on the gear output shaft. The

rotation of the link produces a vertical motion of the

sling holding patient’s foot, which can be suitably

controlled by the electric motor. Figure 5b shows a

3D rendering of the ankle actuator, including

motor+gear, crank, link and connection to the

Lokomat exoskeleton.

As shown in Figure 6, the mechanism has a gear

ratio between the rotation of the gear output shaft

and the rotation of the link which is almost constant

and equal to 1:2.5. Figure 7 shows a picture of the

developed device.

A MECHATRONIC DEVICE FOR THE REHABILITATION OF ANKLE MOTION

Figure 4: Passive sling of LOKOMAT.

(a) (b)

Figure 5: a) Concept of active ankle actuation; b)

Mechanical design of the ankle actuator.

Figure 6: Gear ratio of kinematic mechanism versus angle

of crank α.

Figure 7: The developed device.

5 CONTROL DESIGN

A relevant part of the research consisted in the

design of the control system for the electro-

mechanical ankle actuator. A typical control

architecture for electrical motors is composed of an

internal feedback loop (called current loop) and an

external feedback loop which in this case was

defined to control the angular position of the motor

(position loop), as shown in Figure 8. This

configuration enables to increase the performances

of the control system and to control at any time the

electrical motor current in order to avoid working

condition potentially dangerous for the electrical

actuator.

The current feedback loop is implemented by the

servoamplifier, which has a very high dynamic

response. Control parameters for the current loop are

optimised by the manufacturer, so it was decided to

use it without any modifications. On the other hand,

the regulator for the position loop was implemented

using a programmable control board (DSP board).

The inputs for the DSP board are the reference

position signal and rotor position measured by an

encoder, whereas the output of the position regulator

is the reference current signal, which is fed into the

current regulator.

Figure 8: Block diagram of control system.

In order to define the reference signal for the

position regulator, first of all a typical wave shape

for ankle angular motion was derived taking into

account the patient’s anthropometry, by means of

numerical simulations supported by measurements,

as described in section 3. Figure 3 shows an example

of reference motion law for ankle rotation.

Then, under the simplifying assumption of having a

constant gear ratio between the output shaft of the

gear and the ankle, the reference for ankle rotation

was converted into a reference for the angular

position of the motor.

In this first stage of study, a proportional-

derivative (PD) regulator has been used for the

design of the position loop. The gains of regulator

were chosen to provide a good performance of

control system and to assure a good dynamic

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

response. For the optimal design of the regulator, a

simple linear model of the ankle actuator was

defined. The model equations are:

LiRv ++⋅=

Ke θ⋅=



iKT

⋅=

(1)

)t(T

mtotm

−η=θ⋅



(2)

where v and i are respectively the voltage and the

current of electrical motor characterized by a

resistance R and an inductance L, e is the

electromotive force, K

and K

are respectively the

speed and torque constants, T

is the torque of

motor, J

is the equivalent moment of inertia of all

parts of device,

is the angular rotation of motor,

tot

is the coefficient of efficiency of the reducer, T

the resistant torque and n the total gear ratio.

For the control design, the resistant torque T

considered as a known noise input signal and for this

reason it’s not considered during the design of

regulator.

Finally, numerical tests were performed to verify

the correct tuning of the gain parameter for the

position regulator, using the more detailed non-

linear model described in section 6.1.

6 SIMULATIONS AND TESTS

FOR FINAL ASSESSMENT

6.1 Multi-physics Simulations

A multi-physics model of the ankle actuator was

established, to verify the correct design of the

system (including the regulator) and to assess its

overall performances. The model is composed of:

– an electro-mechanical component, representing

the electrical motor and the gear (see Fig. 9a);

– an electronic component, reproducing the control

loops implemented in the motor drive (Fig. 9a);

– a multi-body biomechanical component, repre-

senting the lower limb and the mechanical

linkages connecting the motor with the foot

(Fig. 9b).

Contrarily to the simplified model used to perform

the control design stage of the project, the multi-

physics model used for verification and assessment

is fully non-linear and accounts for the interaction

effects between the different components of the

system.

In particular, the linear equation (2), representing in

a simplified way the mechanical component of the

system, is replaced by a non-linear equation for the

gear and by a fully non-linear model of the leg and

of the mechanical linkages.

As far as the gear is concerned, a non-linear

formulation is used, accounting for the different

expression of power dissipation in the gear

depending on the power flow being directed from

the motor to the output shaft or vice-versa (Hannah,

Hiller, 1995), so that having defined the mechanical

power flowing in the gear from the motor to the

output shaft W

according to the following

expression:

(

)

mmmmg

JTW

θθ



−=

(3)

the mechanical equation of the motor takes the

following non-linear expression:

0for

⎟

⎠

⎞

⎜

⎝

⎛

+=+

⎟

⎠

⎞

⎜

⎝

⎛

+=+

ηη

θηη



(4)

where J

is the moment of inertia of the rotor and

gear input shaft, J

is the moment of inertia of the

gear output shaft,

and

are the efficiency

coefficients of the gear (for other symbols, see

Section 5).

The leg and the linkages in the ankle actuator are

represented by a multi-body model with an excess of

30 states defined in ADAMS/LifeMOD environ-

ment. The model takes as input the rotation of the

gear output shaft

defined as:

(5)

and by solving the direct dynamic problem for the

linkages and leg returns the motion of the modelled

bodies and the value of the resistant torque T

, which

is fed back into equation (4). The use of the non-

linear multi-body model allows to represent in full

detail the actual non-constant gear ratio of the

linkage (see Figure 6), and to take into account the

effect of actual loads (e.g. contact forces exchanged

in the footprint) in the calculation of the resisting

torque T

, avoiding the simplifying assumptions that

were introduced for control design purposes.

The model was implemented in Matlab/Simulink

environment, using co-simulation with ADAMS to

account for the coupling between the electro-

A MECHATRONIC DEVICE FOR THE REHABILITATION OF ANKLE MOTION

mechanical and electronic components of the model

(implemented in Simulink) and the bio-mechanical

model component (implemented in ADAMS).

Figure 9a shows a high-level representation of the

complete Simulink model, where co-simulation with

the ADAMS subsystem is represented.

(a)

(b)

Figure 9: a) Co-simulation model; b) detail of ADAMS

subsystem.

Figure 10 shows the results of a simulation

reproducing the behaviour of the ankle actuator

under the reference motion law shown in Figure 3

and considering 75% of body weight support. In the

upper subfigure, the deviation of motor rotation with

respect to the reference value is plotted: it is

observed that the maximum deviation is in the range

of 0.3%, indicating that the design of the regulators

was performed correctly, so that the actuator is able

to track position reference within accuracy levels

that are fully satisfactory for the considered

application.

0 0.5 1 1.5 2

-0.5

0.5

ankle angle error

t[s]

[%]

0 0.5 1 1.5 2

-5

motor current

t[s]

[A]

0 0.5 1 1.5 2

-50

motor voltage

t[s]

[V]

Figure 10: Co-simulation results.

In the central and lower subfigures of Figure 10,

motor voltage and current are plotted, together with

their respective limit values that cannot be exceeded

to prevent damage and ensure durability of the

motor. It is observed that for both voltage and

current the maximum values achieved during the

simulation are well below the limit values,

demonstrating the correct dimensioning of the motor

and actuator for the considered application.

In order to quantify the further ability of the

device to withstand higher working loads (produced

e.g. by unforeseen additional disturbances or by

uncertainties in some design parameters), safety

factors can be defined for voltage and current as the

ratio between the limit value and the actual

maximum absolute value of each quantity. For

motor voltage, the safety factor is 1.70 whereas for

motor current the safety factor is 1.32. These values

are high enough to ensure the robustness of the

system, but not so high to suggest the over-

dimensioning of the motor.

6.2 Tests on a Demonstrator

Preliminary tests were performed on the physical

demonstrator shown in Figure 7, to assess

experimentally the performances of the device. At

the present stage of the research, the demonstrator is

not yet connected to the patient’s leg, so passive

masses are used to produce a resisting torque and

inertial effect reproducing in first approximation the

connection with the ankle.

In this section, three working conditions are

considered:

a) An unloaded condition, which means that no

external or inertial load is applied on the ankle

actuator;

b) A loaded condition obtained by connecting a 5kg

mass to the extremity of the sling, thus

introducing a resisting force of about 50N and an

additional inertial effect;

c) A loaded condition realised through a 10kg

mass, producing a resisting force of about 100N

and an inertial effect higher than in case b).

Tests were performed on the ankle actuator by using

the reference ankle rotation represented in Figure 3

and measuring the actual motor position and the

motor current.

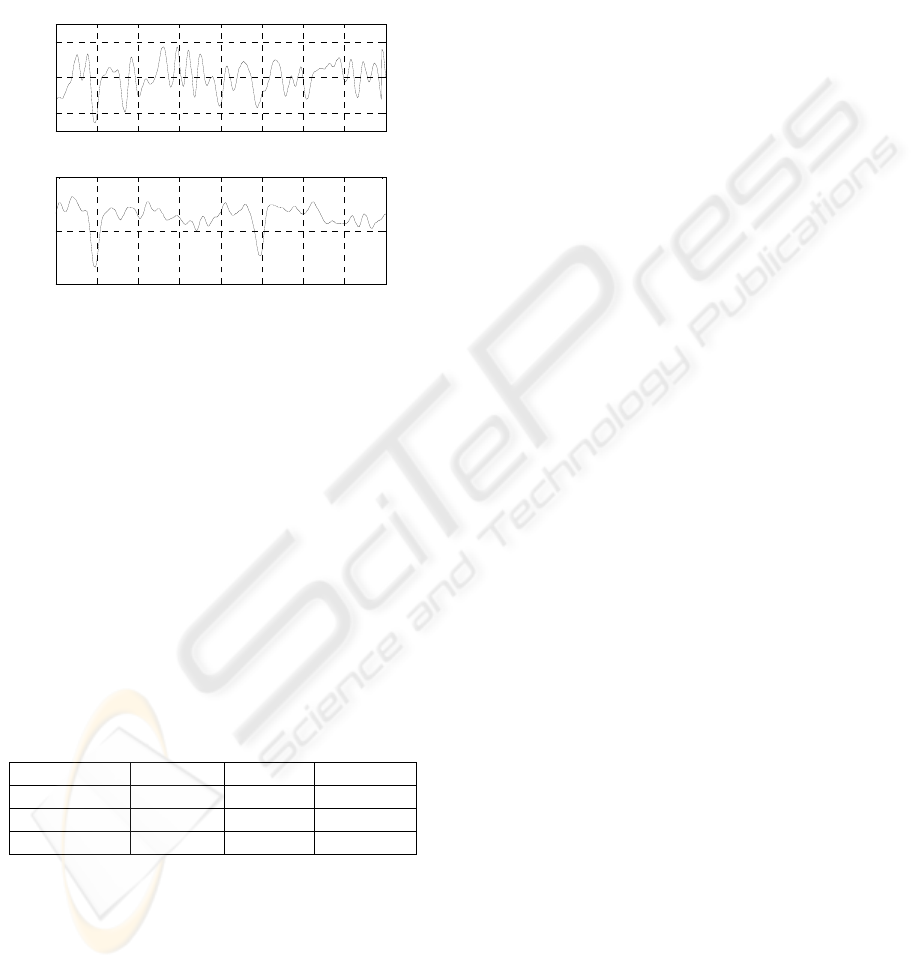
Figure 11 shows the results obtained for working

condition c) in the list above, corresponding to the

most loaded condition. It is observed that the

positioning error is always below 2%, which is a

quite low value but still higher that the one obtained

from the numerical simulation. This result could

however be affected by some electrical noise

disturbance in the measure of the motor angular

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

position, so that the actual positioning error could be

in the same range of values as the one obtained by

numerical simulation. More accurate tests are

planned in order to clarify this point.

The motor current is quite low, with maximum

value below 1A, to be compared with a limit value

of 3.33A. This means that there is a large margin for

further loading of the actuator.

0 0.5 1 1.5 2 2.5 3 3.5 4

-2

ankle angle error

t[s]

[%]

0 0.5 1 1.5 2 2.5 3 3.5 4

0.5

motor current

t[s]

[A]

Figure 11: Experimental result in 100N load condition.

Up: position error; down: motor current.

Table 4 compares the results of tests performed in

working conditions a) to c), in terms of maximum

angular position error of the motor and of maximum

and r.m.s. value of the motor current required by the

actuator. The maximum position error in the

unloaded condition is much higher than in the two

loading conditions. This is produced by the effect of

plays that are present in the mechanical parts

connecting the final link with the gear output shaft.

The effect of plays is otherwise eliminated by the

presence of the gravitational load applied by the

masses in working conditions b) and c).

Table 4: Values of maximum ankle angle error, maximum

motor current and RMS motor current in different loading

condtions.

Error

max

RMS

No load 5.12% 0.42A 0.1A

50N load 1.95% 0.71A 0.59A

100N load 2.55% 0.82A 0.64A

Considering a different working condition where the

ankle actuator is connected with the patient’s leg, the

effect of plays can seriously affect the performances

of the system, and therefore a new stage of the

research was started to find an alternative design for

the connection between the gear output shaft and the

final link moving the patient’s foot. A solution based

on the use of toothbelt was developed and is

presently under realisation. This new solution is

expected to improve substantially the performances

of the device in actual working conditions.

7 CONCLUSIONS

The paper has reported some results from an

ongoing research having as objective the

development of an electro-mechanical ankle actuator

for use in the rehabilitation of lower limb motion in

patients suffering neurological disease.

Preliminary results obtained by numerical

simulation and tests show the ability of the

developed system to actuate ankle motion within

accuracy levels that are appropriate for rehabilitation

purposes. Research is on going on introducing this

device in physiotherapy. Preliminary test on healthy

and diseased subjects are foreseen in a short time.

ACKNOWLEDGEMENTS

The work presented here was made possible through

the financial support of CARIPLO foundation within

the HINT@Lecco (Health Innovation Network

Technology@Lecco) research project.

REFERENCES

Colombo G, Joerg M, Schreier R, Dietz V., 2000.

Treadmill training of paraplegic patients using a

robotic orthosis. Journal of Rehabilitation Research

and Development 37(6):693-700.

M. Bocciolone, M. Lurati, M. Vanali, F. Molteni. Force

measurement during gait therapy assisted by a robotic

treadmill – The case of Lokomat, proposed as poster

presentation for the BIODEVICES 2008 Conference,

Funchal, Madeira, 28-31 January 2008.

G.S. Sawicki, K.E. Gordon e D.P. Ferris, 2005. Powered

lower limb orthoses: applications in motor adaptation

and rehabilitation. 9th International Conference on

Rehabilitation Robotics, June 28 - July 1, 2005,

Chicago, IL, USA.

D. P. Ferris, J. M. Czerniecki, B Hannaford, 2005. An

anckle-foot orthosis powered by artificial pneumatic

muscles. Journal of Applied Biomechanics, 21, pp

189-197.

A.M. Sabatini, C. Martelloni, S. Scapellato, F. Cavallo,

2005. Assessment of walking feature from foot inertial

sensing. IEEE transactions on biomedical engineering

52(3):486-489.

J. Hannah, M.J. Hillier, 1995. Applied Mechanics,

Longman scientific &technical Editions.

A MECHATRONIC DEVICE FOR THE REHABILITATION OF ANKLE MOTION