AN RFID TRANSPONDE
R
LOCATION SYSTEM
Mou Tang, Graeme Chester and Jeffrey Neasham
School of Electrical, Electronic and Computer Engineering, Newcastle University, Newcastle upon Tyne, UK
Keywords: CDMA, Location, RFID Transponder.
Abstract: This paper describes a location system based on RFID technology. This system can be used to map the
image of an endoscope. Compared with other endoscope location systems, this is a wireless system. The
transponder mounted along the shaft of an endoscope does not increase the size of the endoscope or affect
the flexibility of endoscope. We build the mathematical model of this location system and verify this model
by experiments. Although experiments are for a transponder moving along one dimension, we can develop a
three-dimensional system based on our results.
1 INTRODUCTION
The magnetic endoscope imager (MEI) system was
developed independently by (Bladen, 1993) and
(Williams, 1993). The physical principles of the
three-dimensional location system are
straightforward. The image of the endoscope is
mapped in three dimensions using a set of coils that
are installed in the instrument along the shaft. Coils
measure the rate of change of the magnetic field flux
according to Faraday’s law of induction: the change
in magnetic flux through the coil produces a voltage
in the coil circuit. Since the voltage depends
uniquely on the location (x-y-z) and orientation
(
ϕ
θ
− ) of coil, it is possible to get the location and
orientation information of each coil. This
information is collected several times each second,
and is used to map the image of the endoscope.
The dimensions of the coil are critical to
sensitivity (and to some extent to location accuracy).
The larger is the coil, the greater is the sensitivity.
However to fit the physical size of an endoscope, a
typical size of coil is 1 cm long along the axis of
instrument. Low frequency fields render the body
transparent and low field strengths ensure safety
(Bladen, 1993).
One advantage of a magnetic imager system is
the elimination of the need to pass a separate
imaging catheter during procedures, thereby freeing
the accessory channel for suctioning, lavage, and
therapeutic manoeuvres (Friedland, 2002). The other
advantage is that the loops in the path of endoscope
become clear in the MEI system (Bladen, 1993)
compared with a conventional radiological imager
system.
Research work by (Bladen, 1993), (Wehrmann,
2002), (Shah, 2002) and (Geng, 2004) proves that
MEI is a reliable and accurate method. The systems
studied in their work are cabled systems. Voltage
signal are communicated by leads connected to coils.
The more coils that are used, the more leads are
mounted along the shaft of instrument. The leads
increase the diameter and affect the flexibility of the
instrument. In this paper, we describe a wireless
location system which can be a replacement of the
previous cabled system. In our system, we replace
the coils with RFID (Radio Frequency Identification)
transponders which load the read circuit in a
changing pattern over time and identify each
transponder by ID information stored in it.
2 RFID & CDMA BACKGROUND
We identify each transponder by ID information
stored in it. Here, we use spread-spectrum codes to
program transponders. The following parts describe
the characteristics of RFID and CDMA technology
and explain the reasons why we use spread-spectrum
codes to program RFID transponders in our system.
2.1 RFID Technology
RFID technology has existed for many decades. An
RFID system consists of two components: RFID
transponder and reader (Finkenzeller, 2003).
249
Tang M., Chester G. and Neasham J. (2008).
AN RFID TRANSPONDER LOCATION SYSTEM.
In Proceedings of the First International Conference on Biomedical Electronics and Devices, pages 249-255
DOI: 10.5220/0001049002490255
Copyright
c
 SciTePress

Normally the reader is connected to a computer and
used to read and write data. The RFID transponder is
programmed with a unique code and located on
object to be identified. The RFID transponder can be
active or passive (Weinstein, 2005). The built-in
battery of the active transponder increases its size
and limits its applications. In this paper, when we
say RFID transponder, it is a passive transponder.
Passive transponders operate at different
frequencies. As mentioned before, we chose a low
frequency transponder in our system. The size of the
passive transponder can be as small as several
millimetres, such as TK5552 (Atmel, 2003) which is
only 12 mm long with plastic housing. The length of
TK5552 is almost the coil’s length used in (Bladen,
1993). The power in the electromagnetic field
received from the reader is the only power used for
the data transmission between reader and
transponder (Finkenzeller, 2003).
The operating principle of the RFID transponder
is transformer-type coupling between transponder
and reader. When the transponder is in a magnetic
field, the alternating current in the reader coil
induces a current in the transponder’s antenna coil
and this current is used to power the transponder
electronics. ID infromation stored in the transponder
is sent back to the reader by loading the
transponder’s coil in a changing pattern over time,
which affects the induced e.m.f. in the reader (Want,
2004). This process is called load modulation.
2.2 CDMA Technology
As described in Part 1, we find the image of the
endoscope by locating transponders installed along
the shaft of the endoscope. Our system is a wireless
system, and all transponders share the same
frequency resource, so the received signal is a
combination signal from all transponders. To
separate each transponder’s signal at the receiver,
we program each transponder with a different
spread-spectrum code. When the received signal
goes through a corresponding correlator, each signal
is separated individually. But this does not mean we
can use an unlimited number of transponders in our
system. MAI (Multiple Access Interference) is a
factor which limits our system performance.
The other reason that we use spread-spectrum
code is to increase SNR. We know the modulation
method for RFID system is load modulation. Since
the RFID transponder we used is very small
(diameter of TK5552 is less than 3 mm) (Atmel,
2003), and it works at a long distance (up to 35 cm),
the coupling of transponder coil and reader coil is
very weak. This results in the voltage variation on
the reader coil being very small. The location and
orientation of each transponder are calculated by this
voltage. To get accurate location information, we
need to increase SNR. The definition of processing
gain of a spread spectrum system tells us if the
spread-spectrum code is N bits long, the processing
gain is N (Proakis, 2001) and SNR in dB increases
by
NSNR
improved 10
log20=
(1)
Now we can see, by combinating RFID and
CDMA techonology, it is possible to replace wired
coils in previous systems with RFID transponders.
3 LOCATION THEORY
To estimate each transponder’s location (x-y-z),
three pairs of circular coils are used in this system.
Each axis has a pair of parallel co-axial reader coils
like Figure (3). We use two parallel reader coils
instead of one reader coil on each axis for two
reasons. One reason is to get powerful enough fields
to activate the RFID transponder, and the other is to
cancel the effects due to modulation index. Part
4.1.2 gives the explanations in details.
We start from a simple case: the transponder
moves along the x direction. If we can locate a
transponder which moves along the x-axis or moves
along a trail parallel to the x-axis, it is possible for
us to extend it to three dimensions by replication.
The detected voltage signal at the reader coil is
an induced voltage which depends on the mutual
inductance of the reader coil and transponder coil.
To locate a transponder is to find out the
mathematical relation of this induced voltage and
distance between reader coils and transponder coil.
This part aims to find out this relation.
3.1 Mutual Inductance of Coils
The Biot-Savart law tells us that the magnetic field
flux density B at any point P of a circular coil can be
calculated by (Stratton, 1941):
)](
)(
)(
)([
2
22
222
0
kE
xra
xra
kK
I
B
axis
+−
−−
+=
η
π
μ
(2)
)](
)(
)(
)([
2
22
222
0
kE
xra
xra
kK
r
x
I
B
radius
+−
++
+−=
η
π
μ
(3)
BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices
250

X
Y
Z
P(x,y,z) Baxis
BBradius
Figure 1: B-field of a circular coil.
0
μ
is the permeability constant of free space;
I is the current in the coil;
() []
2
1
2
2
1
xra ++
=
η ;
a is the radius of the reader coil;
x is the distance to the reader coil;
[]
2
1
22
zyr += is the distance to axis of reader
coil;
22
)(
4
xra
ar
k
++
=
;
K(k) and E(k) are complete elliptical integrals of
the first and second kinds.
When a small single loop coil is in the field of
this circular coil, we assume that small coil is
situated in a uniform flux density B. The mutual
inductance of two coils is
I
SBSB
M
radiusaxis
αα sincos +
=
(4)
S is the plane area bounded by the small coil;
α
is the angle between S
v
and the x-axis.
Equation (4) gives the relationship between
mutual inductance and distance of two coils.
3.2 Induced Voltage
Assuming a transponder moving in the x direction,
we only need the pair of parallel coaxial reader coils
on the x-axis to determine the transponder’s
x-location. Our RFID location system’s topology for
a pair of reader coils is shown in Figure 2. It is a
3-coil coupling system. This means that the received
signal at any reader coil is a combination of signal
from transponder coil and signal from the other
reader coil.
In the system, AC power source is used to drive
two reader coils and generate magnetic fields to
activate RFID transponder. It does not contribute to
the received signal.
AC
R
C
L
R
C
L
Reader Coil 1 Reader Coil 2
Transponder
coupling
couplingcoupling
Rs
Figure 2: Topology of RFID transponder location system.
A real system’s arrangement looks like Figure 3.
Reader Coil 1 Reader Coil 2
Transponder
1,10
xM
2,20
xM
DM
2
,12
Figure 3: Three coils coupling system.
10
M is the mutual inductance of reader coil-1
and transponder;
20
M is the mutual inductance of reader coil-2
and transponder;
12
M is the mutual inductance between reader
coils;
1
x is the distance of transponder to reader coil-1;
2
x is the distance of transponder to reader coil-2;
2D is the distance between two reader coils.
Assume the complex current in the transponder
is
0
I , and
tj
eI
ω
0
=
0
I . The induced complex voltages
on reader coil-1
10
V and on reader coil-2
20
V are
010
IV
10
Mj
ω
=
(5)
and
020
IV
20
Mj
ω
=
(6)
Complex current
20
I in reader coil-2 due
to
20
V is,
2
0
2
20
20
Z
I
Z
V
I
20
Mj ω ==
(7)
AN RFID TRANSPONDER LOCATION SYSTEM
251

where
2
Z is the total impedance of terminals 2a and
2b in Figure 4.
The induced voltage on reader coil-1
12
V due
to
20
I is
2
0
12
Z
I
V
2012
2
MM ω −=
(8)
So the received complex voltage on reader coil-1 is
2
0
01
Z
I
IV
2012
2
10
MMMj ωω −=
(9)
In the same way, we can find the received
complex voltage on reader coil-2 is
1
0
02
Z
I
IV
1012
2
20
MMMj ωω −=
(10)
where
1
Z is the total impedance of terminals 1a and
1b in Figure 4.
Two reader channels are symmetric, so we have
21
ZZZ ==
(11)
When the distance of two reader coils is fixed,
the mutual inductance of two reader coils
12
M is a
constant. We define
Z
12
M
ω
λ =
(12)
Equation (9) and (10) are
)(
2010
MjM
λ
ω
−
=
01
IV
(13)
and
)(
1020
MjM
λ
ω
−
=
02
IV
(14)
When we only take the coupling data signal into
account, the system in Figure 2 can be converted
into Figure 4. There are two signal sources in
system
1
V and
2
V . Both of them contribute to the
received signal at reader coils.
When the resonant frequency of two read
channels is equal to the frequency of AC power
source, the impedance of the read channel is
resistive and
λ
in Equation (12) is real. The received
complex signal at reader coil-1
r1
V is
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
1
20
2
10
1
10
2
20
2
ρρ
λ
ρρ
ω
MM
j
MM
L
0r1
IV
(15)
where
s
s
RR
RRR
+
+
=
2
2
1
ρ
and
s
s
R
RRR 2
2
2
+
=
ρ
.
R
C
L
R
C
L
Reader
Coil 1
Reader
Coil 2
Rs
1
V
2
V
1a
1b
2a
2b
Figure 4: Simplified system topology.
The amplitude of received signal on reader coil-1
1r
V is
2
1
20
2
10
2
2
1
10
2
20
0
2
1
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
ρρ
λ
ρρ
ω
MMMM
LIV
r
(16)
The amplitude of received signal at reader coil-2
2r
V is similar to reader coil-1
2
1
10
2
20
2
2
1
20
2
10
0
2
2
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
ρρ
λ
ρρ
ω
MMMM
LIV
r
(17)
The ratio of two received signal is
()( )
()()
2
2
2
2
2
2
2
1
1
1
ratioratio
ratioratio
r
r
MM
MM
V
V
−+−
−+−
=
ρλρ
ρλρ
(18)
where
2
1
ρ
ρ
ρ = and
20
10
M
M
M
ratio
= .
3.3 Induced Voltage and Distance
Equation (2), (3) and (4) tell us when the
transponder only moves in the x direction, M is a
function of x and
α
. Equation (4) is:
),(
sincos
α
α
α
xF
I
SBSB
radiusaxis
=
+
(19)
BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices
252

),(
),(
2
1
α
α
xF
xF
M
ratio
=
(20)
xDx +=
1
and xDx −=
2
),(
),(
),(
α
α
α
xM
xDF
xDF
M
ratio
=
−
+
=
(21)
We define
[][ ]
[][]
[][ ]
[][]
1
),(1),(
1),(),(
1
),(1),(
1),(),(
2
2
2
2
2
2
2
2
2
2
2
2
21
21
+
−+−
−+−
−
−+−
−+−
=
+
−
=
αρλαρ
αρλαρ
αρλαρ
αρλαρ
xMxM
xMxM
xMxM
xMxM
VV
VV
V
rr
rr
ratio
(22)
The left of Equation (22) is
ratio
V , which is
determined by the received signal at two reader coils.
The right of Equation (22) is a function of
transponder’s location x. Equation (22) gives out the
relation of received signal at two reader coils and the
location of the transponder. We will explain why we
use voltage ratio
21
21
rr
rr
VV
VV
+
−
to describe our system in
Part 4.1.2.
4 EXPERIMENTS
In Part 3 we gave the mathematical description of
the location system. The theory is validated by
experimental measurements in this section and it
will be shown that the system performs as predicted,
even though some difficulties arise in
implementation.
4.1 Problems in Implementation
4.1.1 Physical Size Effects and Calibration
In Part 2, we assume the RFID transponder is an
ideal small point and the reader coils are filamentary.
This means that the physical sizes of transponder
and reader coils are not taken into account. But for a
real system, this is not true. The physical centres of
the read coils and the transponder are not the
magnetic centres of the read coils and the
transponder any more. To make sure the theory in
Part 2 works, we should choose a transponder as
small as possible. And we need to determine the
effective magnetic centres of the transponder and
two reader coils.
The magnetic centre can be determined by
experiments. First, we estimate any point of a
transponder as magnetic centre and put the
transponder at any point of the axis in two opposite
directions like Figure 5. If this point is the real
magnetic centre of transponder, the voltage ratios for
these two directions should be the same. Otherwise
we need to adjust the estimated centre position until
the two ratios are equal.
Reader Coil 1 Reader Coil 2
Transponder
Direction 1Direction 2
Figure 5: Determination of the magnetic centre of reader
coils and transponder coil.
After we find the magnetic centre of the
transponder, we can use the transponder to
determine the original point of our location system.
Moving the transponder along the axis of the reader
coils, the point which satisfies the voltage ratio in
Equation (22) equal to zero is the centre of the
reader coils and is the original point of the location
system as well.
4.1.2 Modulation Index
The transponder is powered by the magnetic fields,
so the strength of the magnetic fields also affects the
received signal. Figure 6 is our measured
modulation index of the RFID transponder TK5552
used in our experiments. And Figure 6 agrees with
TK5552’s data sheet.
0 50 100 150
0.1
0.2
0.3
0.4
0.5
0.6
Magnetic Fields Strength Hpp(A/m)
Modulation Index
Figure 6: Modulation index versus field strength.
AN RFID TRANSPONDER LOCATION SYSTEM
253

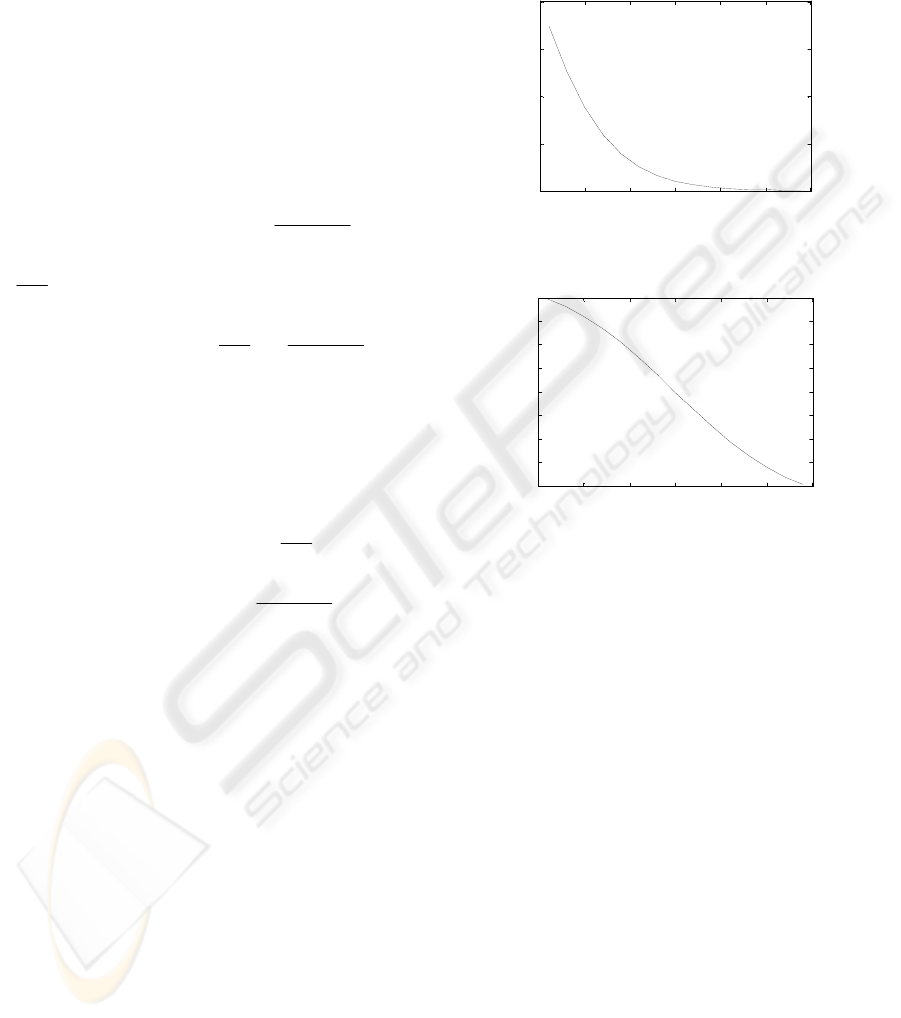
It is clear that the modulation index is not a
constant. This means that the received signal is not
only dependent on the distance but also affected by
the modulated index. This is why we use voltage
ratio (between two parallel reader coils) instead of
voltage itself to describe our location system in Part
3.
The non-constant modulation index means there
is no determinate relation between voltage of
received signal and transponder’s location. If we use
a voltage ratio based system, modulation index
effects are cancelled. In fact, when we use voltage
ratio, the numbers of turns in the reader coils and
transponder coil are cancelled as well.
In Part 3, we use voltage ratio
21
21
rr
rr
VV
VV
+
−
instead
of
2
1
r
r
V
V
to describe our system. Figure 7 and Figure
8 are voltage ratio curves of
2
1
r
r
V
V
and
21
21
rr
rr
VV
VV
+
−
when
the transponder moves along the x-axis. The signal
received on one reader coil becomes small when the
transponder is close to the other one. Due to the
limited precision of the ADC used to capture data,
there is an error in the received signal. From
Figure 7, we can see that an error in a small received
signal will result in a large error in
2
1
r
r
V
V
. To reduce
this quantisation error, we use
21
21
rr
rr
VV
VV
+
−
to derive
position as shown in Figure 8.
4.1.3 Constant
λ
and
ρ
In Equation (22), we define two constants
λ
and
ρ
,
once the system is built, the values of these are also
determined. However it is difficult to determine their
exact values by the definition in Part 3 for a real
system. Fortunately Equation (22) tells us
that
λ
and
ρ
can be estimated by voltage ratio and
distance.
[]
),(,
,
α
ρ
λ
xVX
ratio
=
(23)
In Part 4.1 we have determined the original
centre of the location system, so it is possible to
measure a transponder’s location and angle. By
putting a transponder at any point on the axis, we
can get a set of voltage ratio and location data. Using
two sets of voltage ratios and locations (
1ratio
V ,
1
x )
and (
2ratio
V ,
2
x ), we can estimate the values
of
λ
and
ρ
. To get a much more accurate calculation
of
λ
and
ρ
, we can use several sets of (
ratio
V ,
x
) at
different points to estimate their values.
-0.1 -0.05 0 0.05 0.1 0.15
0
5
10
15
20
Sensor Location x(m)
Vr1/Vr2
Figure 7: Voltage ratio curve of Vr1/Vr2.
-0.1 -0.05 0 0.05 0.1 0.15
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
Sensor Location x(m)
(Vr1-Vr2)/(Vr1+Vr2)
Figure 8: Voltage ratio curve of (Vr1-Vr2)/(Vr1+Vr2).
4.2 Experiment Results
After solving the problems faced in a real system,
we have constructed a system to verify our theory in
Part 3. The parameters of the system are as follows:
 The number of reader coil turns N=20;
 The radius of reader coil a=24.5 cm;
 The separation of two reader coils= 35.6 cm;
 RFID transponder is TK5552;
 The constant
046.0
=
λ
and 13.0=
ρ
.
Our experiments measure a transponder moving
along the x direction. To extend a one dimension
system to three dimensions, we need to test the
transponder moving not only along the x-axis, but
also along trails parallel to the x-axis. We also need
to take angle into account. Since three axes are
orthogonal each other, we only measure the worst
case: angle is 45 degrees. When the angle is beyond
45 degrees with one axis, it means the angle with
another axis is smaller than 45 degrees.
Figures 9 to 11 are experimental results. Figure 9
shows voltage ratio curves for a transponder moving
along the axis. Figure 10 and 11 are voltage ratio
BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices
254

curves for a transponder moving along a trail
parallel to the x-axis (y=-15cm, z=0cm). Each figure
has two curves. One is the voltage ratio from
experiments, and the other one is calculated by
Equation (22).
The results show that our mathematical equation
in Part 3 can correctly describe our system. Figure
10 tells us that Equation (22) still works when the
transponder is off axis. Figure 11 shows that the
transponder still works when the angle is 45 degrees.
Experimental results show that it is possible to
develop a three-dimensional system based on our
experiments, and this is the subject of ongoing
research.
-0.1 -0.05 0 0.05 0.1 0.15
-1
-0.5
0
0.5
1
Location of Sensor x(m)
Vratio
Vratio from Experiment
Vratio in Theory
Figure 9: Vratio when transponder moves along x-axis
(
0=
α
).
-0.1 -0.05 0 0.05 0.1 0.15
-1
-0.5
0
0.5
1
Location of Sensor x(m)
Vratio
Vratio from Experiment
Vratio in Theory
Figure 10: Vratio when transponder moves along a trail
parallel to x-axis (y=-15cm,
0
=
α
).
-0.1 -0.05 0 0.05 0.1 0.15
-1
-0.5
0
0.5
1
Location of Sensor x(m)
Vratio
Vratio from Experiment
Vratio in Theory
Figure 11: Vratio when transponder moves along a trail
parallel to x-axis (y=-15cm,
o
45= α
).
5 CONCLUSIONS
In this paper, we describe a location system based on
RFID technology. Although our experiments are for
a one-dimensional system, the results and analysis
show it is possible to develop a three-dimensional
system. Also spread-spectrum coding, which is used
to program transponders, lets us track multiple
transponders. Using this location system with
multiple RFID transponders, we expect to be able to
map the images of endoscopes without attaching
extraneous wires.
REFERENCES
Bladen, J.S., Anderson, A.P., Bell, G.D., Rameh, B.,
Evans, B., Heatley, D.J., 1993. Non-radiological
technique for three-dimensional imaging of
endoscopes.
Lancet, 341, pp.719-22.
Williams, C., Guy, C., Gillies, D., Saunders, B., 1993,
Electronic three-dimensional imaging of intestinal
endoscope.
Lancet, 341, pp.724-725.
Friedland S., Van Dam J., 2002. A global positioning
system for the colon.
Endoscopy, 34(11), pp.900-4.
Wehrmann, K., Fruhmorgen, P., 2002. Evaluation of a
New Three-dimensional Magnetic Imaging system for
Use During Colonoscopy.
Endoscopy, 34(11),
pp.905-8.
Geng, D., 2004.
High Refresh Rate Three Dimension
Positioning System Using Frequency-Multiplexed
Electromagnetic Fields. Ph.D. Newcastle University.
Finkenzeller, K., 2003.
RFID Handbook, Carl Hanser
Verlag. Munich, Germany, 2
nd
edition.
Weinstein, R., 2005, RFID: A Technical Overview and Its
Application to the Enterprise
. IT Professional, 7(3),
pp.27-33.
Atmel, 2003. Read/Write Transponder TK5552.[online].
Available from: http://www.atmel.com/dyn/resources/
prod_documents/doc4698.pdf, [cited 8 July 2007].
Want, R., 2004. The Magic of RFID.
ACM Queue,
October, pp.41-8.
Landt, J., 2005. The History of RFID.
Potentials, IEEE,
24(4), pp.8-11.
Proakis, J.G., 2001.
Digital Communications, McGraw
-Hill Company. Boston, 4
th
edition.
Stratton, J.A., 1941. Electromagnetic Theory, McGraw
-Hill Book Company, Inc. New York, 1
st
edition.
AN RFID TRANSPONDER LOCATION SYSTEM
255