WIDE-BANDWIDTH, HIGH FRAME RATE ELECTRICAL

IMPEDANCE TOMOGRAPHY / SPECTROSCOPY

A Code Division Multiplexing (CDM) Approach

A. L. McEwan, D. S. Holder

Department of Medical Physics and Bioengineering, University College London, Gower St London, UK

J. Tapson

Department of Electrical Engineering, University of Cape Town, Cape Town, South Africa

A. van Schaik

School of Electrical and Information Engineering, University of Sydney, Sydney, Australia

Keywords: Electrical impedance tomography, electrical impedance spectroscopy, bioimpedance measurement, code

division multiplexing.

Abstract: We present a proposal and proof-of-concept, experimental results for a new type of electrical impedance

tomography / spectroscopy system that makes use of code division multiplexing to achieve two important

technological advances. Assigning each channel an orthogonal code allow all the impedance measurements

to be made simultaneously in time, thereby increasing the frame rate; and the use of pseudorandom input

signals allows a very wide range of frequencies to be sampled simultaneously in each channel.

1 INTRODUCTION

Electrical impedance tomography (EIT), in which a

volume is probed non-invasively by injecting

currents (or magnetic fields) and measuring the

electrical potential or magnetic fields at the

periphery, has been used for physiological imaging

for three decades (Holder, 2005). Its applicability in

industrial situations, in which it is called process

tomography, was recognized in the early 1980’s

(Beck and Williams, 1996), leading to a

considerable investment in research into hardware,

software, and reconstruction algorithms (West,

2002). More recently, there has been a growing

interest in obtaining material contrast in the images

by discriminating on the basis of the frequency

response of impedance; this is electrical impedance

spectroscopy (EIS) (Brown, 2001). The combination

of the two methods is generally called EITS.

In the standard implementation of EIT, the

complex impedance is measured in terms of

resistance and capacitance. A ring of (usually 8 or

16) electrodes is placed around the volume to be

imaged (generally, a single plane or slice is imaged,

and volumes reconstructed from a number of planes;

hence the use of the word tomography). A current is

injected through a pair of the electrodes, and the

resulting electrical potentials measured at all of the

other electrodes. The signals are separated into a

resistive and a capacitive signal, either by measuring

the complex impedance directly, or by using

separate ohmic and capacitive electrodes.

If the frequency of the injected current is swept

through a range, or stepped through a set of fixed

frequencies, the spectral response may also be

obtained. The current excitation is then switched to a

new pair of electrodes, and a new data set acquired.

When all the desired combinations have been

measured, a reconstruction algorithm is used to

produce an approximation of the distribution of

material within the image plane, based on its

impedance (in EIT) or impedance spectrum (in

EITS). The reconstruction of EITS images is an area

of active research, and many different methods are

available (Polydorides and Lionheart, 2002).

There are a number of standard patterns of

excitation and measurement in EITS. The most

commonplace is that adjacent pairs of electrodes are

196

L. McEwan A., S. Holder D., Tapson J. and van Schaik A. (2008).

WIDE-BANDWIDTH, HIGH FRAME RATE ELECTRICAL IMPEDANCE TOMOGRAPHY / SPECTROSCOPY - A Code Division Multiplexing (CDM)

Approach.

In Proceedings of the First International Conference on Biomedical Electronics and Devices, pages 196-203

DOI: 10.5220/0001049601960203

 SciTePress

used to inject current, and potentials are measured at

all other adjacent pairs. This method has the

advantage that once a pair of electrodes has been

used for current injection, and its response at all

other electrodes measured, it is thereafter redundant

to measure potentials at that pair and therefore the

number of measurements required is reduced.

Regardless of the pattern used, a single frame of EIT

data requires a great many measurements (the

adjacent-pair method requires k = n×(n-1)

measurements for n electrodes); and this number

must be multiplied by the number of frequency

points required.

Taking a frame of EIT data using sequential

measurements – so-called time-division multiplexed

or TDM measurements) is slow, so that frame rates

in excess of 100 frames/second are extremely

difficult to achieve. Wilkinson and co-workers

(2003) have optimized the TDM process to a very

high degree, achieving frames rates of up to 1000

frames/s; but most laboratory and commercial

systems operate at orders of magnitude slower than

this. EITS systems are slower still, with frame rates

of 13 seconds/frame achievable with a frequency

range of 20 Hz – 128 kHz in current systems

(McEwan et al., 2006). A basic constraint in EITS

frame rate is imposed by the lower limit of spectral

bandwidth; for example, if the impedance at 20Hz is

required, the frame rate per second will be limited to

20/k, where k is the number of sequential

measurements required per frame; even this limit

implies sampling only a single cycle of the lowest

frequency per measurement, which is somewhat

difficult to achieve in practice.

A method which presents itself for increasing the

frame rate is simultaneously to inject currents which

are modulated to be mathematically orthogonal, so

that their contributions to the potential at any

electrode can be separated by demodulation. For

example, if a current of frequency f

is injected at

one pair of electrodes, and a current of frequency f

at a second pair, then the potential across a third pair

of electrodes can be separated into a component due

to f

and a component due to f

by synchronously

demodulating with those frequencies. The complex

components of impedance can be extracted by in-

phase and quadrature synchronous demodulation.

This is called frequency-division multiplexed (FDM)

EIT.

FDM EIT appears to have been developed

simultaneously by Tapson and colleagues (Tapson &

Teague, 2002), and Zimmermann and colleagues

(Zimmermann et al., 2002); although as both

developments were patented and not published in the

scientific literature, public domain details are few

(Teague, 2002).

A number of problems are encountered in FDM

EIT as a consequence of accommodating

simultaneous current injection and voltage

measurement on the same electrode. If the current

and voltage form part of the same impedance

calculation, this comprises a two-terminal

impedance measurement; whereas it is generally

considered that a four-terminal measurement is

required to avoid the problem of inadvertently

including the contact or terminal resistance in the

specimen resistance. If the current and voltage form

part of a separate calculation, then this problem is

avoided.

A second issue is that the current through any

terminal must be a sum of orthogonal component

currents, and equal and opposite components must

flow through some other terminal. Ensuring that the

net current due to each component is zero is

electronically complicated, and has not been

attempted in any of the known FDM EIT systems.

These systems have generally avoided these

problems by using separate sets of current injection

and voltage measurement electrodes, although this

has the disadvantage that twice the number of

electrodes are required to obtain the same resolution.

Data comparing the resolution of FDM and TDM

systems is scarce (Goldswain & Tapson, 2006), but

those results as well as unpublished work (Elliot,

2006) suggest that FDM systems are at least as

accurate as TDM systems.

In this paper we present a new approach to EITS

instrumentation. We make use of Code-Division

Multiplexing (CDM) to inject orthogonal currents

simultaneously, and to demodulate the resulting

potentials. This has an enormous advantage over

FDM and TDM techniques, in that it is possible to

sample at multiple frequencies simultaneously while

sampling multiple physical channels. The result is a

system in which wide-bandwidth multi-electrode

spectroscopy can be performed in times equivalent

to that taken for single measurements in current

EITS systems. The CDM process can be seen as a

natural extension of FDM EIT, and many of the

same issues apply. In order to deal with the problem

of sharing electrodes between multiple measurement

channels, we have developed a simple current

injection arrangement at the electrode, based on

high-frequency transformers, which guarantees a net

zero current flow for each orthogonal component.

The new system is described in detail in the

following sections.

WIDE-BANDWIDTH, HIGH FRAME RATE ELECTRICAL IMPEDANCE TOMOGRAPHY / SPECTROSCOPY - A

Code Division Multiplexing (CDM) Approach

197

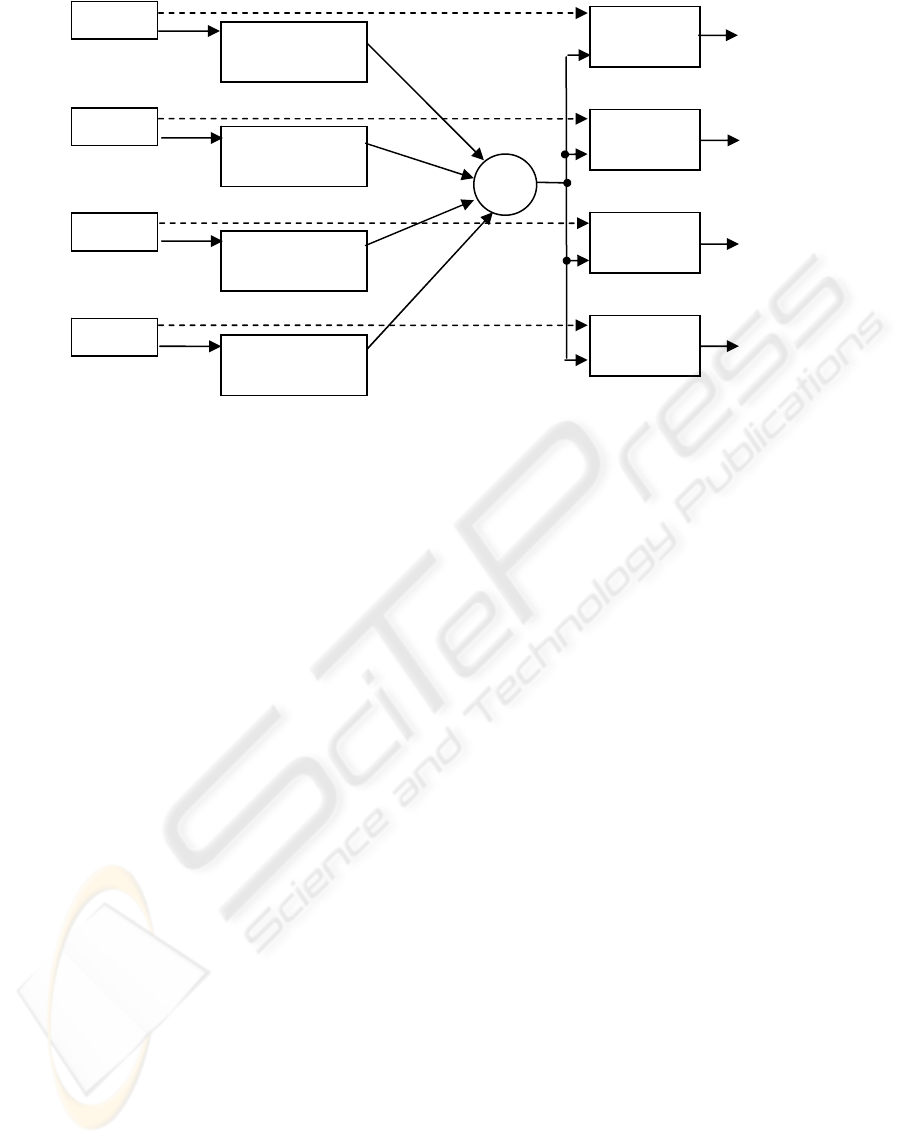
Figure 1: The code-division multiplexing principle. Each unique channel in the measurement system is stimulated using a

driving signal modulated with a unique binary pseudorandom (PRN) code. The channels are then either deliberately or

inadvertently mixed together. At the receivers, the contribution due to each channel is recovered by cross-correlating the

signal at the receiver, and a copy of the driving signal containing the channel’s characteristic code. If the codes are

orthogonal or near-orthogonal, there should be complete separation of components. Serendipitously, the cross-correlation

produces the impulse response of the channel (see Equations 1-6).

2 CODE-DIVISION

MULTIPLEXING OF EIT

CHANNELS

The principle of CDM is that the signal through a

particular channel is modulated using a unique

binary digital code (see Figure 1). A receiver which

is receiving several channels can separate the data

for each channel by demodulating using a copy of

the same code. There are a number of different

codes which may be used. The basic requirements

are that there should be at least one code per

channel; that the codes should be orthogonal, or

nearly so; and that the autocorrelation functions of

the codes should be flat with a single sharp peak (in

the ideal case, approximating a delta function)

(Sarwate & Pursley, 1980). The codes which we

have used in this work are called Gold codes, and

are used in the Global Positioning System (GPS) to

encode the signals from the GPS satellite

constellation; these signals can then be

unambiguously demodulated by a terrestrial GPS

receiver equipped with copies of the codes

(Parkinson & Spilker, 1996). The codes are bit

sequences which appear to be random, but in fact are

deterministically generated, usually by means of a

modulo-addition of bits in a shift register. Codes of

this type are generally referred to as pseudorandom

noise (PRN) sequences, as they appear to be random

and have the characteristics of noise.

In this system, we achieve two important goals

using CDM. Firstly, the use of CDM allows us to

take measurements over all the channels

simultaneously. Secondly, the spectral

characteristics of the CDM input signal effectively

interrogate the sample over a wide range of

frequencies, and the output signals can be

transformed to produce a spectrum, giving us

simultaneous wide-band spectroscopy on all

channels. The following two sections explain these

features.

2.1 The Use of Code Division

Multiplexing to Provide

Simultaneous Measurement

The use of CDM in an EIT system is shown

conceptually in Figure 1. We use the PRN codes as

the input stimulus to a system. The system has a

unique channel for each input, but unfortunately all

the channel outputs are combined linearly, so that

the unique response for each channel is not

explicitly available.

When we perform a cross-correlation R

between the unique input signals I

and the

combined output signal O

, we are calculating:

code 1

code 2

code 3

code 4

unique

channel h

(t)

unique

channel h

(t)

unique

channel h

(t)

unique

channel h

(t)

cross

correlate

cross

correlate

cross

correlate

cross

correlate

(t)

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

198

∑

−

)(

mnnOI

mR (1)

where N is the epoch length of the PRN (nominally,

1023 bits, or the equivalent number of samples).

The output at any time k can be stated as the sum

of the convolution of the impulse responses for the

channels and the respective inputs:

11() 22() 33()

00 0

...

kk k

k i ki i ki i ki

ii i

OIh Ih Ih

−−−

== =

=+ ++

∑∑ ∑

(2)

If we substitute this into the cross-correlation,

say for I

and the output:

...

)(

)(221

)(111

)(221

)(11

)(33

)(22

)(11

⎢

⎣

⎡

∑∑

−

−−

−

−−

−

−−

−

−−

−

−−

−

−−

−

−−

−

imnin

imni

nOI

hII

hIhI

hII

(3)

Given that:

∑∑

−

kik

iki

hIhI

1)(1

)(11

(4)

We can rearrange as follows:

)(

...)(

)(

...

)(

2)(21

1)(11

himR

hII

iII

iimnn

iimnnOI

+−

+−=

∑

∑∑

−

−−

−

−−

(5)

The cross-correlation terms (those R

terms with

non-identical indices for I) will sum to zero, because

different Gold codes are effectively uncorrelated; so

only the first correlation is non-zero. In continuous

terms:

)(

)()(

)()()(

111

tht

thtRtR

IIOI

∗=

∗

(6)

The output of the cross-correlation is the impulse

response of the channel, which represents the time-

domain transform of the information we want.

2.2 Hardware Implementation

Part of the proposed hardware implementation is

shown on the following page, with a number of

elements not shown to improve clarity. We use

transformer coupling of the drive currents to the EIT

electrodes in order to ensure matched source and

sink currents. There is a resistor in each transformer

secondary, to allow direct measurement of the

current in the secondary. The way in which the

system works is as follows. The microprocessor

system outputs currents which are modulated in

polarity by the Gold codes (using push-pull drive

from two port pins, with a series resistor for current

limiting). Each of the eight transformer secondaries

is connected to a pair of electrodes, so that each

electrode is connected to the high side of one

secondary and the low side of another.

In principle, the current between terminals T1

and T2 should have a fixed amplitude, modulated in

polarity by Code 1. In practice, we measure this

current by sampling the voltage at the points V

and

, and dividing the difference by the resistor

value.

We can then calculate the impulse response for

the voltage between T

and T

, with respect to the

current between T

and T

, by cross-correlating the

voltages (V

- VT

) and (V

– V

); and so on.

2.3 Spectral Response of the CDM

System

As discussed earlier, PRN sequences have the

appearance of noise, and like uniformly distributed

white noise, their spectrum is flat within the limits of

bandwidth. They are also delta-correlated; that is to

say, their autocorrelation function consists of a Dirac

delta function at the origin. This is the basis of their

usefulness in demodulation, as shown above. From

(6) above we see that the input-output cross-

correlation function of a channel in the system pro-

WIDE-BANDWIDTH, HIGH FRAME RATE ELECTRICAL IMPEDANCE TOMOGRAPHY / SPECTROSCOPY - A

Code Division Multiplexing (CDM) Approach

199

Figure 2: Block diagram of the proposed system, showing multiple electrodes at which drive and reception of signals is

combined. Transformer coupling allows inflowing and outflowing currents due to each code to be exactly balanced, as well

as providing isolation for safety. The voltage across each ballast resistor gives the current due to that code (e.g. the current

due to Code 3 is I

= (VT

- V

)/R

duces the transfer function h(t) of the channel. If we

take the Fourier transform of the cross-correlation

function:

)(

)()(

dteth

dtetRG

∫

∞

∞−

−

∞

∞−

−

(7)

so, the Fourier transform of the cross-correlation

function produces the frequency response of the

channel; which is to say, the complex spectrum of

the channel impedance.

3 PROOF OF CONCEPT –

EXPERIMENTAL RESULTS

3.1 Method

In order to establish the workability of this concept,

we require to demonstrate two methods:

• The feasibility of extracting wide-range, high

resolution impedance measurements when

driving the channels with PRN codes.

• The feasibility of simultaneously stimulating

several channels and recovering the

individual signals from the multiplexed

signal by demodulation.

We have done this as a proof-of-concept by

conducting an imaging experiment with an existing

EITS system, using both the standard sinusoidal

waveforms, and a new waveform based on the Gold

code intended for CDM-EIT.

A serial, EITS system, the UCL Mk2.5, was

reprogrammed with the 1

1023-length code of a set

of eight Gold codes. Only one code was used as the

Mk2.5 is based on a single channel of the Sheffield

Mk3.5 system multiplexed to 32 electrodes. In

normal operation the Mk2.5 system measures the

spectrum using a 2048-length composite waveform

of 10 frequencies of equal amplitude,

logarithmically spaced between 2kHz and 1MHz

(McEwan et al., 2006; Wilson et al., 2001). The

Gold code was sampled at 2samples/bit to meet the

Code 1 Code 2 Code 3 Code 4

microprocessor / FPGA generating PRN codes with push-pull drive

PC with DAQ card sampling 16 channels ADC

– V

and

– VT

omitted for

clarity

Volume or

sample under

test

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

200

Nyquist criteria with an additional zero bit added to

ensure its length was 2

. This is required by the

matched filter which is performed by the system

DSP processor. As the length of both test waveforms

are the same, and the timing of the system clock

(2MHz) was unchanged, they span the same

frequency range of 2kHz-1MHz. For simplicity, and

to ensure that the instrumentation did not saturate,

the amplitude of the gold code waveform was set to

the maximum of the composite waveform.

An often used test of an EITS system is its

ability to produce images of an object in a tank filled

with saline solution. Boundary voltage

measurements are collected from the tank with and

without the object (so-called perturbation and

reference frames). These two sets of data are

subtracted then used with a reconstruction algorithm

to produce a time-difference image. In keeping with

previous EITS measurements we chose to use a

piece of banana as our object, as it changes

impedance by over 100% between 2kHz and 1MHz

(Yerworth et al., 2003). The saline solution’s

impedance will remain relatively unchanged over

the same frequency range and hence it is possible to

determine the spectrum of the object inside the tank

from a sequence of images at the measured

frequencies.

The tank was cylindrical, 10cm diameter, filled

with 0.1% saline solution with 16 stainless steel

electrodes in a ring. The test object was a cylinder of

banana, 2 cm long and 1 cm in diameter. Image

reconstruction was done using a linear solver

(EIDORS) (Polydorides and Lionheart, 2002) and a

15,000 element FEM mesh of the tank.

3.1.1 Results

The spectra for the banana object were constructed

by plotting the value of a pixel in the known position

of the object, at 10 different frequencies.

x 10

-3

Frequency (kHz)

Voltage(V)

(a)

x 10

-3

Frequency (kHz)

Voltage(V)

(b)

Figure 3: Comparison of boundary voltage measurements

in a single frame. Each line is a different electrode

combination measurement. Larger voltages occur when

the voltage electrodes are near current-carrying electrodes.

Combinations more sensitive to the perturbation show a

greater change over frequency. Figure 3(a) shows a

composite representation of the output of the standard 10

frequency system. Figure 3 (b) shows the output of the

new system, using PRN codes for excitation and

demodulation. It can be seen that the PRN codes provide

the same response as the standard method, but with a

much higher resolution in frequency.

WIDE-BANDWIDTH, HIGH FRAME RATE ELECTRICAL IMPEDANCE TOMOGRAPHY / SPECTROSCOPY - A

Code Division Multiplexing (CDM) Approach

201

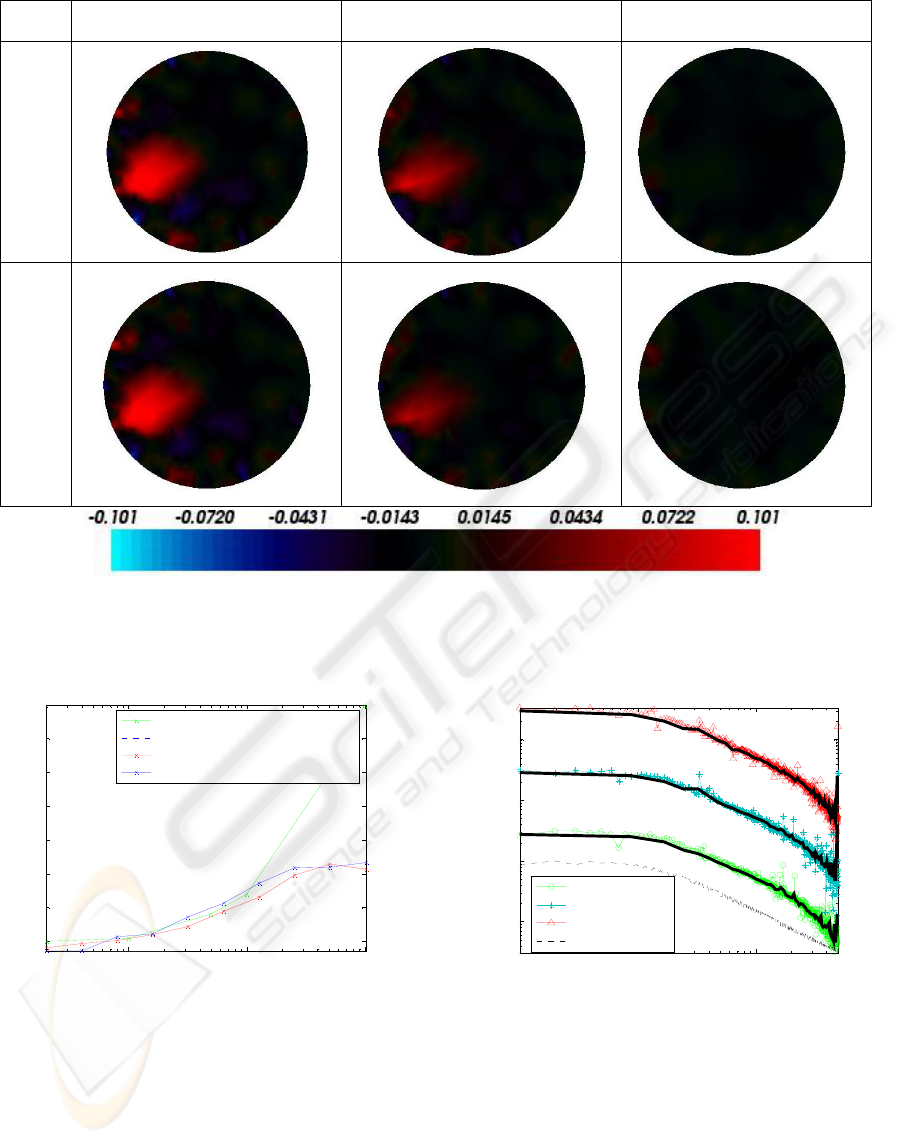
Figure 4: Time difference images collected at three frequencies using the two waveforms. As the frequency increases, the

contrast (impedance difference) between perturbation and background decreases. It can be seen that the new PRN (Gold

code) method offers the same resolution as the standard 10-frequency method, with the potential for significantly faster

operation.

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

Frequency (kHz)

Conductivity (S/m)

direct Z measurement, banana

Nacl

10 frequency composite waveform

Gold code

Figure 5: Spectra obtained from the data used in Figure 4.

These spectra are similar to those that have been

previously obtained from the Mk2.5 system. The new

method produces a spectrum which is very similar to the

standard method. Both EITS spectra deviate from a direct

measurement at frequencies above 128kHz, for reasons

explained below.

-1

Frequency (kHz)

Magnitude

3ch 1st channel

3ch 2nd channel

3ch 3rd channel

1ch only

Figure 6: Spectral magnitude for three multiplexed

channels, independently stimulated with PRN codes,

mixed together on a single circuit impedance, and then

demodulated. For clarity each channel has been multiplied

by 10

where x is the channel number. It can be seen that

the multiplexed signals can be independently recovered

after mixing, and are a good match (although noisier) to

the single channel case. The thick black lines show a

average spectra, possible due to the large number of

frequencies available in this method.

2kHz 64kHz 512kHz

10 frequency

composite waveform

Gold code waveform

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

202

4 DISCUSSION

The boundary voltages measurements using the two

waveforms are similar, as shown in Figure 3. The

PRN code voltage measurements are 1mV lower,

due to the lower current per frequency component.

As this is constant between the perturbation and

reference frames, it is cancelled out in the

subtraction process and is not apparent in the

images. The PRN code boundary voltages appear to

be noisier, particularly at higher frequencies. In

practice these frequencies would be averaged

together reducing the noise. The Mk2.5 EIT system

has limited performance at frequencies above

128kHz due to the effect of 0.5m long unscreened

cables. These are likely to be the cause of the

increased noise seen in the PRN code spectra, a real

effect which is not seen in the lower frequency

resolution of the 10 frequency composite waveform.

The 128kHz limit is also apparent in the spectra,

which deviate from a direct impedance measurement

above this frequency.

We have shown the feasibility of using PRN

codes for EITS, both in extracting the system

impulse response, and in terms of simultaneous

excitation and demodulation. The images and

extracted spectra are very similar to those obtained

using the standard method, demonstrating the proof

of the concept of using CDM waveforms for EIT

acquisition. The primary advantage of greatly

increased frequency resolution for the same

acquisition time has been demonstrated. We are

currently implementing a multiple source system

which should lead to a system with two orders of

magnitude increase in frame rate over the standard

method, along with the improved frequency

resolution demonstrated here.

ACKNOWLEDGEMENTS

Action Medical Research RTF 3110 and The

University of Sydney International Visiting

Research Fellowship 2007.

REFERENCES

Beck, M.S. & Williams, R.A. (1996). Process

tomography: a European innovation and its

applications, Meas. Sci. Technol. , 7, 215–24.

Brown, B.H. (2001). Medical impedance tomography and

process impedance tomography: a brief review, Meas.

Sci. Technol., 12, 991-996.

Elliot, J. (2006). Electrical impedance tomography

imaging of a hydrocyclone, M.Sc thesis (University of

Cape Town).

Goldswain, G., & Tapson, J. (2006). Kernel ridge

regression for volume fraction prediction in electrical

impedance tomography, Meas. Sci. Technol., 17,

2711-2720.

Holder, D.S. (ed.) (2005). Electrical Impedance

Tomography: Methods, History and Applications,

Bristol and Philadelphia: IOP.

McEwan, A., Romsauerova, A., Yerworth, R., Horesh, L.,

Bayford, R., & Holder, D. (2006). Design and

calibration of a compact multi-frequency EIT system

for acute stroke imaging, Physiol. Meas., 27, S199-

S210.

Parkinson, B.W., & Spilker Jr., J.J. (1996). Global

Positioning System: Theory and Applications, vol. 1,

Am. Inst. Aeronautics and Astronautics Inc.,

Washington.

Polydorides, N. & Lionheart W.R.B. (2002). A Matlab

toolkit for three-dimensional electrical impedance

tomography: a contribution to the Electrical

Impedance and Diffuse Optical Reconstruction

Software project, Meas. Sci. Technol., 13, 1871-1883.

Tapson, J., & Teague, G. (2002). Method and Apparatus

for Electrical Impedance Tomography, SA Patent

2002/3689.

Teague, G. (2002). Mass Flow Measurement of Multi-

Phase Mixtures by Means of Tomographic

Techniques, PhD thesis, (University of Cape Town).

retrieved June 24, 2007 from

http://mysite.mweb.co.za/ residents/ jontapson/

Sarwate, D.V., & Pursley, M.B. (1980). Crosscorrelation

properties of pseudorandom and related sequences,

Proc. IEEE, 68, 593-619.

West, R. (ed,) (2002). Special Feature: Process

Tomography, Meas. Sci. Technol,. 13, 1799-1902.

Wilkinson, A.J., Randall, E.W., Durrett, D., Naidoo, T. &

Cilliers, J.J. (2003). The design of a 1000 frames per

second ERT data capture system and calibration

techniques employed. Proc. 3rd World Congress on

Industrial Process Tomography, Banff, 504-509.

Wilson, A.J., Milnes, P., Waterworth, A.R., Smallwood,

R.H., & Brown, B.H. (2001). Mk3.5: a modular,

multi-frequency successor to the Mk3a EIS/EIT

system, Physiol. Meas., 22, 49-54.

Yerworth, R.J., Bayford, R.H., Brown, B., Milnes, P.,

Conway, M. & Holder, D.S. (2003). Electrical

impedance tomography spectroscopy (EITS) for

human head imaging, Physiol. Meas., 24, 477-489.

Zimmermann, E., Glaas, W., Verweerd, A., Tillmann, A.,

& Kemna, A. (2002). Method and apparatus for rapid

tomographic measurements of the electrical

conductivity distribution of a sample, German patent

DE 102 38 824.

WIDE-BANDWIDTH, HIGH FRAME RATE ELECTRICAL IMPEDANCE TOMOGRAPHY / SPECTROSCOPY - A

Code Division Multiplexing (CDM) Approach

203