PULSE-TYPE NEURO DEVICES WITH SPIKE TIMING
DEPENDENT SYNAPTIC PLASTICITY
Katsutoshi Saeki,Yugo Hayashi
College of Science and Technology, Nihon University, Funabashi-shi, Chiba, Japan
Yoshifumi Sekine
College of Science and Technology, Nihon University, Funabashi-shi, Chiba, Japan
Keywords: Neural Network, Pulse-Type, STDP, Synaptic Weight, Neuro Device, Noise Tolerance.
Abstract: Even though the neurons in the human brain are sensitive to noises, human central nervous systems can
operate correctly under a noisy environment. Since neural networks have superior information processing
functions, many investigators have attemptted to model biological neurons and neural networks. A number
of recent studies of neural networks have been conducted with the purpose of applying engineering to the
brain. Especially, neuro devices have been created that focus on how to have a learning function. Here, we
focus on spike timing dependent synaptic plasticity (STDP) and construct pulse-type neuro devices with
STDP using analog VLSI technology. We show that it is possible to extract phase differences representing
the reinforcement part of the synaptic weight by using pulse-type neuro devices with STDP. Moreover, we
investigate noise tolerance for thermal noise and fluctuation of time.
1 INTRODUCTION
An artificial neural network that performs similarly
to the human brain would be required to construct a
brain-type information processing system. Our
human central nervous systems can operate correctly
in noisy environments even though the neurons in
the brain are sensitive to noise. On the other hand, it
would be necessary to use neuro devices as
components in an environment without noise. To
focus on this superior function, investigators are
studying the noise tolerance of artificial neural
networks. Because it is not possible to learn
correctly when influenced by noise, an information
processing system cannot be constructed. The
classical Hebbian learning rule is proposed as the
learning rule. (Hebb, 1949). This rule is thought to
play an important role in the synaptic plasticity of
neural networks in the brain. This rule uses mean
spike firing correlations between pre- and
postsynaptic neurons to drive learning. Recently,
the form of synaptic plasticity was seen to be
dependent on the order and time intervals of pre- and
postsynaptic spikes (STDP: spike timing dependent
synaptic plasticity (Bi and Poo, 1998, Nishiyama,
Hong, Mikoshiba, Poo, and Kato, 2000)), as was
observed in the hippocampus and cerebral cortex.
(Patrick and Curtis, 2002, Sakai and Yoshizawa,
2003, Tsukada, Aihara, Kobayashi and Shimazaki,
2005). STDP manifests itself as the potentiation of a
synapse if the presynaptic spike precedes the
postsynaptic spike, and as depression if the
presynaptic spike follows the postsynaptic spike.
Potentiation and depression were determined from
the results of experiments on rat hippocampal
neurons (Patrick and Curtis, 2002) and frog tectal
neurons. (Zhang, Tao, Holt, Harris and Poo, 1998).
The timing based learning rule enhances the
excitatory postsynaptic potentials induced by
coincident input spikes, since the synaptic
connections already contributing to postsynaptic
firing are further strengthened. (Gerstner, Kempter,
van Hemmen and Wagner, 1996). It is reported
these characteristics are useful and effective for the
extraction of synchronous firing so that STDP is
buried in the noise. (Fukai and Kanemura, 2001,
Saeki, Hayashi and Sekine, 2006). In addition, the
hardware model with STDP
(Bofill-i-Petit and
Murray, 2004) has been proposed based on the
physiological experiment results. However these
264
Saeki K., Hayashi Y. and Sekine Y. (2008).
PULSE-TYPE NEURO DEVICES WITH SPIKE TIMING DEPENDENT SYNAPTIC PLASTICITY.
In Proceedings of the First International Conference on Biomedical Electronics and Devices, pages 264-268
DOI: 10.5220/0001051702640268
Copyright
c
 SciTePress

models are complex circuits and don’t study the noise
tolerance.
On the other hand, we proposed a pulse-type
neuro device that approximately simulates pulse
signals as an information transmission means in the
brain. (Sekine 1999, Saeki, Sekine, and Aihara, 1999,
Sekine, Sumiyama, Saeki and Aihara, 2001).
In this paper, we discuss the construction of
neural networks from pulse-type neuro devices with
STDP. We show that it is possible to extract the
phase difference representing the reinforcement part
of synaptic weight. Moreover, we investigate the
noise tolerance of thermal noise and the fluctuation
of time.
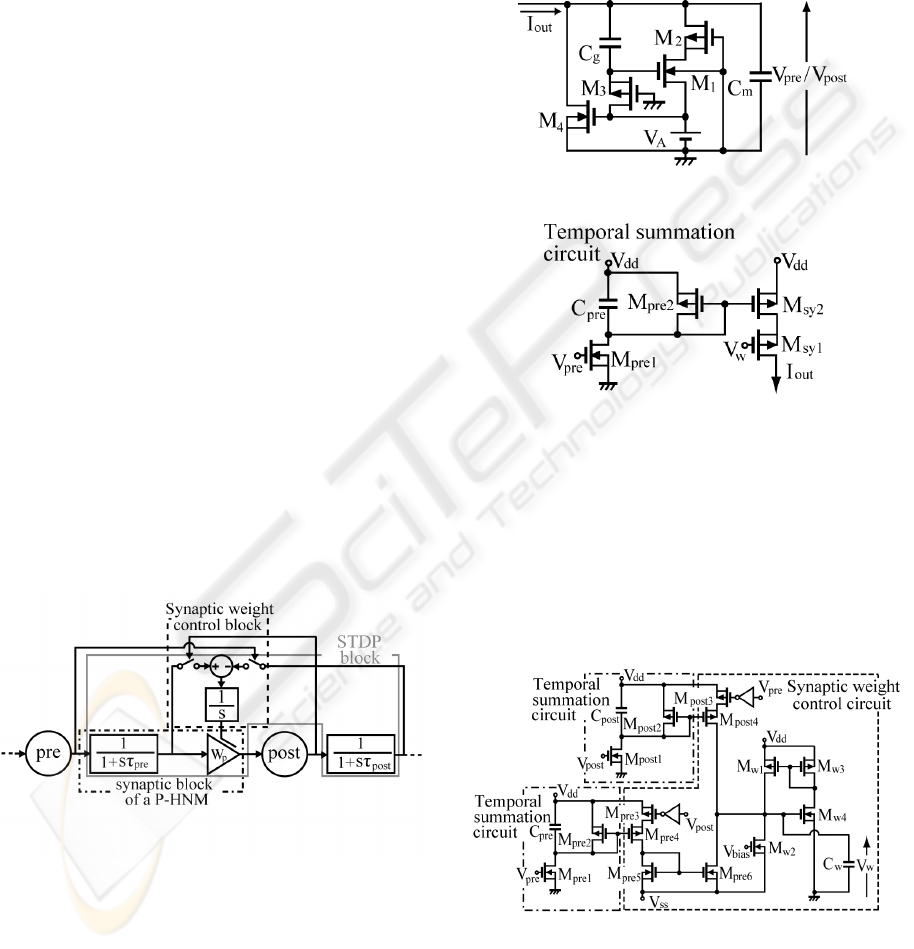
2 CIRCUIT OF NEURO DEVICES
WITH STDP
An STDP block diagram is shown in Fig. 1. This
block diagram has cell body blocks and an STDP
block. When pulses are inputted to each temporal
summation block, output pulses from each temporal
summation block have first-order delays and are
transmitted to the subsequent blocks. When the post-
synaptic cell generates the pulses, the synaptic
weight W
p
between pre- and post-synaptic cells is
reinforced based on the output amplitude of the
temporal summation block with the pre-synaptic
cell. On the other hand, when the pre-synaptic cell
generates the pulses, W
p
is suppressed based on the
output amplitude of the temporal summation block
with the post-synaptic cell.
Figure 1: STDP block diagram.
A pulse-type neuro device is shown in Fig. 2. The
pulse-type neuro device consists of a cell body
circuit and a synaptic circuit. Figure (a) shows the
cell body circuit. When I
out
is inputted to the cell
body circuit, output pulses are generated. This
circuit has a threshold and a refractory period
characteristic. Figure (b) shows the synaptic circuit.
When pulses are inputted to the input terminal V
pre
of the synaptic circuit from the pre-synaptic cell, I
out
is generated. The current I
out
changes according to
V
w
. Therefore, the synaptic weight between the pre-
and post-synaptic cells can be controlled by V
w
.
Spatial summation circuits can also be constructed
when a series circuit of M
sy1
and M
sy2
is connected
in parallel.
Figure 2: Pulse-type neuro device.
The synaptic weight generation circuit is shown in
Fig. 3. This circuit consists in part of three blocks;
two temporal summation circuits and a synaptic
weight control circuit. The voltage V
w
is the output
voltage of this circuit and is the parameter that
controls the synaptic weight between the pre- and
post-synaptic cells.
Figure 3: Synaptic weight generation circuit.
A function of V
w
in the synaptic weight generation
circuit is shown in Fig. 4. The horizontal axis is the
time interval Δt’, which is the time of the pre-
synaptic pulse minus the time of the post-synaptic
(a) Cell body circuit.
(b) Synaptic circuit.
PULSE-TYPE NEURO DEVICES WITH SPIKE TIMING DEPENDENT SYNAPTIC PLASTICITY
265

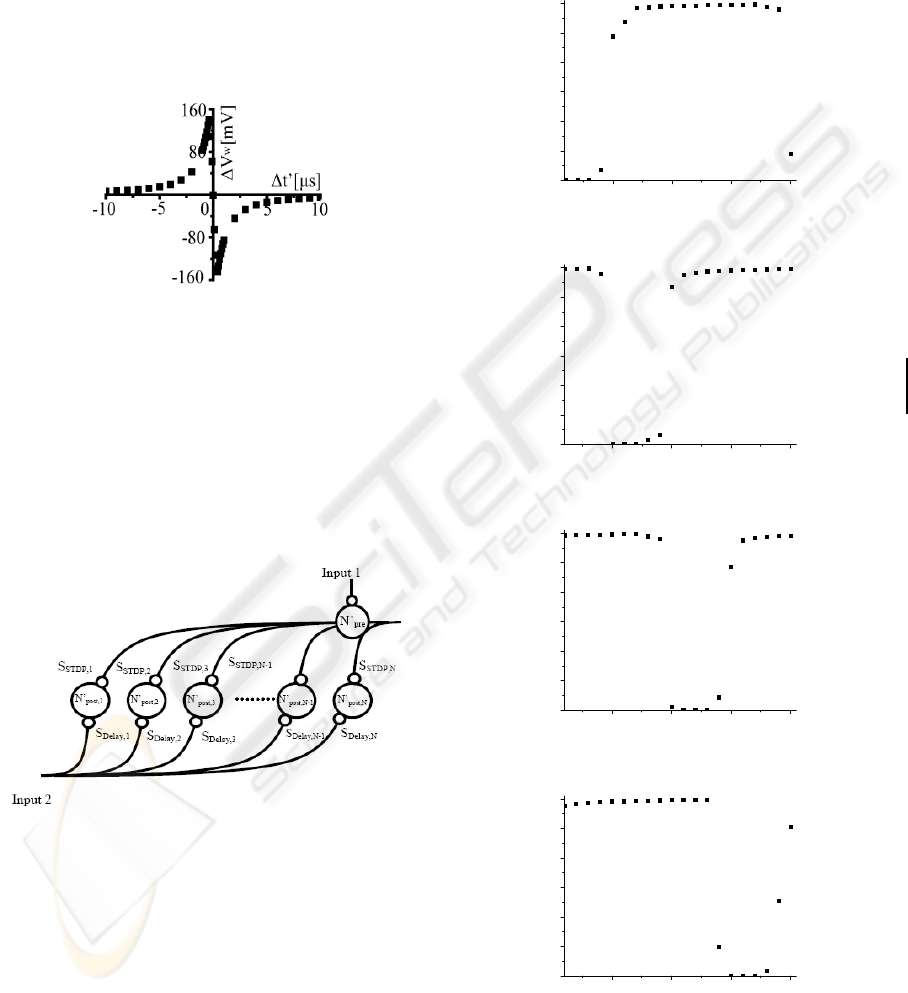
5 101520
0.0
0.5
1.0
1.5
2.0
2.5
3.0
V
w,k
Number of synaptic circuit k
(a) 0 [rad]
5101520
0.0
0.5
1.0
1.5
2.0
2.5
3.0
Number of synaptic circuit k
(b) π/2 [rad]
V
w,k
[V]
5101520
0.0
0.5
1.0
1.5
2.0
2.5
3.0
Number of synaptic circuit
k
(c) π [rad]
V
w,k
[V]
Figure 6: Synaptic weight control voltage.
5101520
0.0
0.5
1.0
1.5
2.0
2.5
3.0
Number of synaptic circuit k
(d) 3π/2 [rad]
V
w,k
[V]
pulse, and the vertical axis is the amount of voltage
change ΔV
w
of V
w
after generating pulses in pre-
and post-synaptic cells. This figure shows that V
w
increases when a pulse generated in the post-
synaptic cell after a pulse is generated in the pre-
synaptic cell, but decreases when the pulse
generated in the pre-synaptic cell follows the pulse
generated in the post-synaptic cell. Furthermore, as
Δt’ becomes shorter, ΔV
w
increases exponentially.
From these results, we clarify principles of the
operation of the proposed circuits when the circuit in
Fig. 2 is controlled with V
w
in Fig. 3. Therefore,
controlling the circuit depicted in Fig. 2 with V
w
, as
depicted in Fig. 3, generates the STDP function.
3 EXTRACTION OF PHASE
DIFFERENCE INFORMATION
Figure 5 shows an example of a neural network
composed of S
Delay,(1~k~L)
that represents the synaptic
circuits of each difference in the propagation delay
time, S
STDP,(1~k~L)
that represents the synaptic circuits,
with synaptic weight control circuits, N'
pre
and
parallel N’
post,(1~k~L)
. Moreover, inputs 1 and 2 are
made in the same cycle. The synaptic weight control
voltage of S
STDP,(1~k~L)
is V
W,STDP(1~k~L)
, and the
synaptic weight control voltage of S
Delay,(1~k~L)
is a
constant value V
W,STDP(1~k~L)
= 0.0 V. The
propagation delay time of S
Delay,k
is assumed to be
the next equation.
)1( −
⋅
Δ
=
k
k
τ
τ
(1)
In equation, τ
k
is the propagation delay time. Δτ is
the sampling time of the propagation delay time.
Figure 5 : A neural network that extracts phase.
Figure 4: Characteristic of V
w
in the synaptic weight.
BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices
266

Input 2 is transmitted N’
post,(1~k~L)
through the
S
STDP,(1~k~L)
, and N’
post,(1~k~L)
outputs pulses at each
different time. The synaptic weigh control voltage of
the synaptic circuit, which connects the cell body
circuit and input 1 corresponds to the phase
difference between inputs 1 and 2, decreases
because the cycles of inputs 1 and 2 are the same. As
a result, the phase difference can be learned as the
number of the synaptic circuit which it reinforces.
Moreover, the cell body circuit connected with the
reinforced synaptic circuit can output a pulse when
input 1 is inputted again after the learning finished,
and the phase difference between inputs 1 and 2 can
be extracted.
Figure 6 shows the characteristics of each
synaptic weight control voltage V
w,k
to the phase
difference of input 2 based on input 1. In this case,
we use the parameters, T=10μs, L=20 and Δτ=0.5μs.
The horizontal axis is the number of the synaptic
circuits, and the vertical axis is V
W,STDP(1~k~L)
. This
figure shows that V
w,k
with the minimum value
neighbourhood appear to be 1~4, 5~9, 12~16 and
17~20 for phase differences between inputs 1 and 2
of 0, π/2, π and 3π/2, respectively. That is to say, the
minimum neighbourhood depends on the phase
difference between inputs 1 and 2. Therefore, it is
possible to extract the phase difference from pulse-
type neuro devices with STDP.
4 NOISE TOLERANCE
4.1 Thermal Noise
In this section, thermal noise is assumed, and
tolerance to white noise is investigated.
The signal of the next equations is used as a
train of pulses that adds white noise to a periodic
train of pulses of the cell body circuit.
∑
=
+⋅=
m
i
whiteiprepre
viTvS
1
,
)'()(' σ
(2)
∑
=
++⋅=
n
j
whitejpostpost
vdtjTvS
1
,
)'()(' σ
(3)
In these equations, v
white
shows white noise that
generates random numbers. σ’ is the standard
deviation of distribution, shows noise tolerance.
In this case, we use these parameters, T=10μs and
dt=1μs.
Figure 7 shows a characteristic of the synaptic
weight control voltage to the strength of the white
noise. The horizontal axis is the strength of the white
noise and the vertical axes are the average of V
w
(■
) and the ratio that becomes V
w
less than 1V (○),
respectively. We assume that it is transmitted to the
pulses from N
pre
to N
post
, when V
w
less than 1V. This
figure shows that not more than σ’ =1.0V is
displayed below V
w
=1.5V, and σ’ =1.05V is
displayed above V
w
=1.5V. Noise strength shows that
if the influence of the reinforcement displays below
σ’ =1.0V, the influence of the suppression appears
as σ’ =1.05V. As well, the rate that V
w
becomes not
more than 1V is 100% within the range of σ’ =0.8V
or less. This suggests a neural network with STDP
that has a learning function with tolerance for white
noise of 0.8V or less.
4.2 Fluctuation of Time
Next, the difference of the pulse timing caused by
the wiring capacity etc. is investigated. The signal of
the next equations is used as a train of pulses that
adds the fluctuation of the timing of the cell body
circuit.
()
∑
=
+⋅=
m
i
iNrandiprepre
tiTvS
1
,,
)"(" σ
(4)
()
∑
=
++⋅=
n
j
jNrandjpostpost
tdtjTvS
1
,,
)"(" σ
(5)
In these equations, t
Nrand,i
t
Nrand,j
show the fluctuation
of time. σ’’ is the standard deviation of the
distribution, showing the noise tolerance. In this
case, we use the parameter, T=10μs.
Figure 8 shows a characteristic of the synaptic
weight control voltage to the fluctuation of the time.
The horizontal axis is σ’’ and the vertical axes are
the average of V
w
(■) and the ratio that becomes V
w
Figure 7: Synaptic weight control voltage to the
stren
g
th of white noise.
0.5 1.0
0
20
40
60
80
100
0.0
0.5
1.0
1.5
2.0
2.5
3.0
σ’ [V]
V
W
ratio
Ratio that becomes V
W
less
than 1V [%]
V
W
[V]
PULSE-TYPE NEURO DEVICES WITH SPIKE TIMING DEPENDENT SYNAPTIC PLASTICITY
267

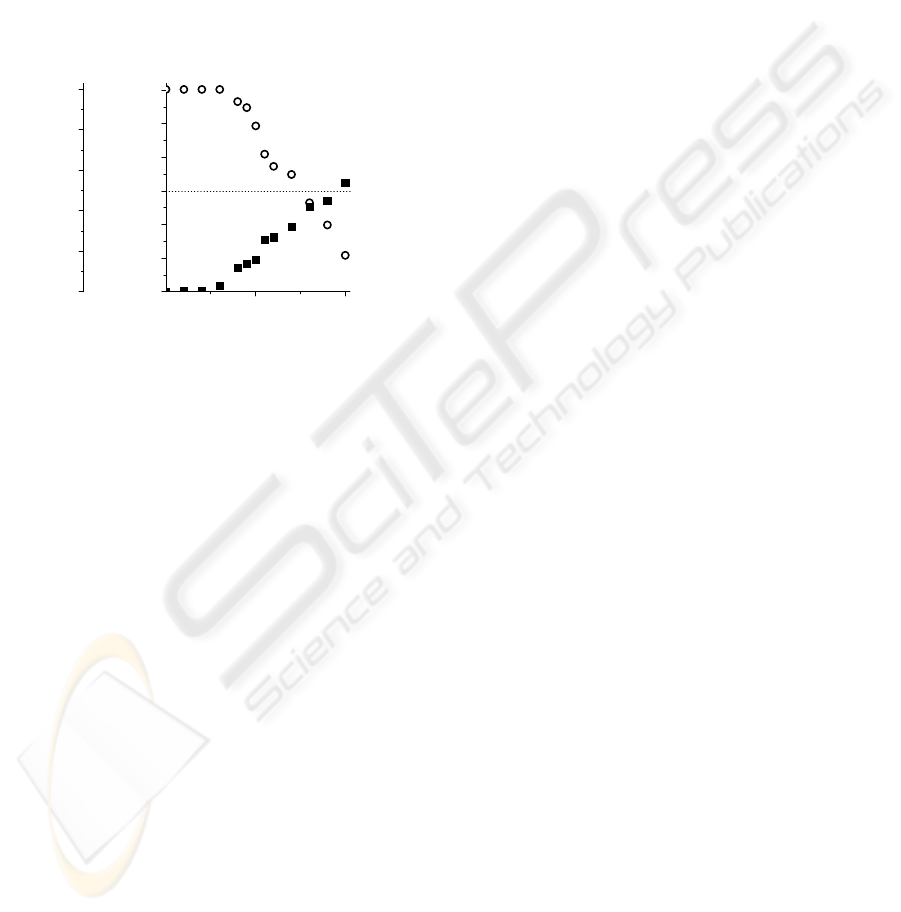
less than 1V (○), respectively. This figure shows
that not more than σ’’ =1.8μs is displayed below
V
w
=1.5V, and σ’’ =2.0μs is displayed above
V
w
=1.5V. The fluctuation of time shows that the
influence of reinforcement is displayed below σ’’
=1.8μs, and the influence of suppression appears at
σ’’ =2.0μs. As well, the rate at which V
w
becomes
not more than 1V is 100% within the range of σ’’
=0.6μs or less. This suggests a neural network with
STDP that has a learning function with tolerance for
the fluctuation of time of 0.6μs or less.
5 CONCLUSIONS
In this paper, we focus on STDP and we construct
neuro devices with STDP to study the effect of
STDP on the ability to extract phase differences.
Using these devices, we construct a neural network
that extracts phase difference information. As a
result, it is possible to extract the phase differences
of pulse-type neuro devices with STDP, representing
the reinforcement component of synaptic weight.
Moreover, we investigated the noise tolerance of the
proposed model. As a result, we demonstrated pulse-
type neuro devices with STDP that have a learning
function with tolerance for white noise of 0.8V or
less, and for fluctuation of time of 0.6μs or less.
That is to say, we showed that pulse-type neuro
devices with STDP had a learning function with
noise tolerance for the thermal noise and the
fluctuation of the time.
In our future work, we will construct an integrated
circuit with pulse-type neuro devices with STDP.
ACKNOWLEDGEMENTS
This work was supported in part by Amano Institute
of Technology.
REFERENCES
Hebb, D. O, 1949. “The organization of behavior, A
Neuropsychological Theory”, New York.
Bi G-q., Poo M-m., 1998. “Synaptic modifications in
cultured hippocampal neurons, Dependent on spike
timing, synaptic strength, and postsynaptic Cell Type”,
J. Neurosci.
Nishiyama M., Hong K., Mikoshiba K., Poo M-m., &
Kato K., 2000. “Calcium stores regulate the polarity
and input specificity of synaptic modification”,
Nature.
Patrick D. R., Curtis C. B., 2002. “Spike Timingdependent
synaptic plasticity in biological systems”, Bio.Cybern.
Sakai Y., and Yoshizawa S., 2003. “Mechanisms of
synaptic competition and regulation in spike-time-
dependent synaptic plasticity rules”, IEICE Technical
Report.
Tsukada M., Aihara T., Kobayashi Y., Shimazaki H., 2005.
“Spatial analysis of spike-timing-dependent LTP and
LTD in the CA1 area of hippocampal slices using
optional imaging”, Hippocampus.
Zhang li I., Tao HW., Holt CE., Harris WA., Poo M-m.,
1998. “A critical window for cooperation and
competition among developing retinotectal synapses”,
Nature.
Gerstner W, K, R., van Hemmen JL., Wagner H., 1996.
“A neuronal learning rule for sub-millisecond
temporal coding, Nature.
Fukai T. and Kanemura S., 2001. “Noise-tolerant stimulus
discrimination by synchronization with depressing
synapses”, Biological Cybernetics.
Saeki K., Hayashi Y.,, Sekine Y., 2006. “ Extraction of
Phase Information Buried in Fluctuation of a Pulse-
type Hardware Neuron Model Using STDP”, 2006
International Joint Conference on Neural Networks
(IJCNN2006).
B-i-P Adria and Murray A, F., 2004, “Synchrony
Detection and Amplification by Silicon Neurons With
STDP Synapses”, IEEE Trans. on Neural Networks.
Sekine Y., 1999. “Pulse-Type Hardware Neuron Model”,
Computer Today.
Saeki K., Sekine Y., and Aihara K., 1999,“A Study on a
Pulse-type Hardware Neuron Model using CMOS,”
International Symposium on Nonlinear Theory and Its
Applications (NOLTA99).
Sekine Y., Sumiyama M., Saeki, K. and Aihara K., 2001.
“ A Λ-Type Neuron Model using Enhancement-Mode
MOSFETs”, IEICE Trans.
1.0 2.0
0
20
40
60
80
100
0.0
0.5
1.0
1.5
2.0
2.5
3.0
ratio
V
W
σ’’ [
μ
s]
Ratio that becomes V
W
less
than 1V [%]
V
W
[V]
Figure 8: Synaptic weight control voltage to fluctuation
of the time.
BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices
268