DEVELOPMENT OF A PARTIAL SUPERVISION STRATEGY TO

AUGMENT A NEAREST NEIGHBOUR CLUSTERING ALGORITHM

FOR BIOMEDICAL DATA CLASSIFICATION

Sameh A. Salem, Nancy M. Salem and Asoke K. Nandi

Signal Processing and Communications Group

Department of Electrical Engineering and Electronics, The University of Liverpool

Brownlow Hill, L69 3GJ, Liverpool, UK

Keywords:

Data clustering, Partial supervision, Retinal blood vessels segmentation, Breast cancer classiﬁcation.

Abstract:

In this paper, a partial supervision strategy for a recently developed clustering algorithm NNCA (Salem et al.,

2006), Nearest Neighbour Clustering Algorithm, is proposed. The proposed method (NNCA-PS) offers clas-

siﬁcation capability with smaller amount of a priori knowledge, where a small number of data objects from the

entire dataset are used as labelled objects to guide the clustering process towards a better search space. Results

from the proposed supervision method indicate its robustness in classiﬁcation compared with other classiﬁers.

1 INTRODUCTION

Data clustering is a common technique for data anal-

ysis, which is used in many ﬁelds, including ma-

chine learning, data mining, pattern recognition, im-

age analysis and bioinformatics. Clustering is the

grouping of individualsin a population in order to dis-

cover structures in the data. In some sense, we would

like the individuals within a group to be close or sim-

ilar to one another, but dissimilar from the individu-

als in the other groups (Webb, 2003; Theodoridis and

Koutroubas, 2003). Recently, a number of clustering

algorithms has been proposed. The basic two types

of clustering algorithms are partitional and hierarchi-

cal algorithms. Their main purpose (Xu and Wunsch,

2005; Jain et al., 1999; Jain and Dubes, 1988) is to

evolve a N

× n partition matrix U(X) of a dataset

X (X = {x

,.. . ,x

}) in R

, representing its parti-

tioning into a number of N

clusters (C

,.. . ,C

The partition matrix U(X) may be represented as

U = [u

], m = 1,.. . ,N

and j = 1, ...,n, where u

is the membership of pattern x

to cluster C

. In hard

partitioning of the data, the following conditions hold:

= 1 if x

∈ C

; otherwise, u

= 0.

Clustering is unsupervised classiﬁcation where

there are no predeﬁned classes (labels) and no a priori

knowledge of the data, while supervised classiﬁcation

requires a complete knowledge of the data where the

class label and the number of classes (labels) are pre-

deﬁned (Bouchachia and Pedrycz, 2006). The pro-

cess of labeling data objects is always an expensive

and error-prone task that requires time and human in-

tervention. In many situations, objects are neither per-

fectly labelled nor completely labelled. Therefore, the

main idea of clustering with partial supervision strat-

egy is to take the advantage of the smaller proportion

of labelled objects to guide the clustering process of

the unlabelled objects.

One of the typical applications of clustering

with partial supervision is Computer-AidedDiagnosis

(CAD) which has become one of the major research

subjects in medical imaging and diagnostic radiology

(Doi, 2005). The basic concept of CAD is to provide

a computer output as a second opinion to assist radi-

ologists’ image interpretation by improving the accu-

racy and consistency of radiological diagnosis (Doi,

2005). The design of clustering with partial supervi-

sion in CAD can play an important role in improv-

ing CAD performance at small amount of knowledge,

where only some labelled objects or regions of an im-

age can assist in identiﬁcation of any suspicious ob-

jects or regions.

This paper proposes a novel partial supervision

strategy for the recently developed clustering algo-

rithm NNCA (Salem et al., 2006). We examine its

applicability and reliability using datasets from real-

world problems, where the proposed method is used

to segment the blood vessels in retinal images which

326

A. Salem S., M. Salem N. and K. Nandi A. (2008).

DEVELOPMENT OF A PARTIAL SUPERVISION STRATEGY TO AUGMENT A NEAREST NEIGHBOUR CLUSTERING ALGORITHM FOR BIOMEDI-

CAL DATA CLASSIFICATION.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 326-333

DOI: 10.5220/0001056503260333

 SciTePress

can help in early detection and diagnosis of many eye

diseases, and it is used to classify breast tumors into

either malignant or benign. Additionally, this paper

presents a comparative evaluation of the proposed al-

gorithm with some other algorithms.

2 THE NNCA CLUSTERING

ALGORITHM

NNCA (Salem et al., 2006) is a modiﬁed version of

the KNN classiﬁer, and it is divided into two stages for

creating N

clusters. First stage is to select N objects

randomly. Then non-overlapping clusters are created

from these N objects, each of maximum size K

init

ob-

jects (the choice of K

init

ensures that more than N

clusters are generated here). Afterwards an iterative

control strategy is applied to update the clusters and

their memberships by increasing the number of neigh-

bours until N

non-overlapping clusters are created.

Second stage is to cluster the remaining objects. For

each unclustered object q, K nearest clustered objects

are found. Then, the cluster to which most of these K

clustered objects belong is deemed to be one to which

the object q belongs to.

The NNCA clustering algorithm is detailed in Al-

gorithm 1. Let each object x be described by the fea-

ture vector:

< a

(x)a

(x),. .. ... , a

(x) >

where a

(x) is used to denote the values of the p-th

attribute of data point x. If we consider two objects x

and x

, then the distance between them is deﬁned as

d(x

), which is expressed in Eq. 1.

d(x

) =

∑

r=1

) − a

))

(1)

A fuzzy clustering, where all objects are allowed to

belong to all clusters with different degrees of mem-

bership, is achieved by obtaining the mean value

of the K nearest neighbours for each object in the

dataset. Therefore, hard partition as well as soft parti-

tion can be obtained. For an object x

to be clustered,

let x

... x

denote the nearest K clustered objects to

and C(x

) ∈ {1,. .., N

} is the cluster index for ob-

ject x

. Hard partition value for x

is:

C(x

) = argmax

n∈N

∑

r=1

δ(n−C(x

)), (2)

and soft partition vector is:

C(x

) =

∑

r=1

δ(C(x

) −C(x

))

(3)

Algorithm 1 Nearest Neighbour Clustering Algo-

rithm (Salem et al., 2006)

Input (data, N, K

init

, N

, K) where:

∗ N is the number of random objects to be clus-

tered.

∗ K

init

is the nearest neighbour objects from N.

∗ N

is the user deﬁned number of clusters.

∗ K is the number of nearest clustered objects.

# Step 1: Create N

non-overlapped clusters

# (a) Create initial clusters:

* Initially, all the N objects are unclustered.

let M = 1

For i = 1 to N

IF ( object i is unclustered )

- Assign i and its unclustered neighbours (from N)

of the K

init

nearest neighbours to cluster # M.

- M = M + 1

End IF

End For

# (b) Merge clusters:

* DO

- K

init

= K

init

+ 1

- Assign each clustered object to the common

cluster of the K

init

nearest neighbours.

- Update the number of clusters → M

WHILE ( M > N

)

# Step 2: Find the nearest K neighbours for each

remaining object

- Assign each unclustered object to the common

cluster of the K nearest clustered objects.

- Use Eq. 2 to ﬁnd hard partition and Eq. 3 to

ﬁnd soft partition.

Output ( Hard partition vector, Soft partition matrix)

Figure 1 shows a sub-image from a colour retinal im-

age and its ground truth along with the corresponding

segmented sub-images after applying NNCA.

3 NNCA WITH PARTIAL

SUPERVISION STRATEGY

(NNCA-PS)

In this section, we propose to adapt NNCA algorithm

with some labelled objects to guide the clustering pro-

cess of the unlabelled objects, i.e., NNCA with partial

supervision (NNCA-PS). The proposed method is di-

vided into two stages. First stage is to select N

ob-

jects randomly from the dataset to be labelled data ob-

DEVELOPMENT OF A PARTIAL SUPERVISION STRATEGY TO AUGMENT A NEAREST NEIGHBOUR

CLUSTERING ALGORITHM FOR BIOMEDICAL DATA CLASSIFICATION

327

(a) (b) (c)

Figure 1: (a) Original sub-image, (b) ground truth sub-image, and (b) sub-image with blood vessels clustered using NNCA.

jects and cluster these N

objects into N

clusters, as

described in Sec. 2. Second stage is to classify each

cluster according to the class label of the majority of

its objects. For each labelled data object x

of class

, assigned to cluster j (1 ≤ j ≤ N

), if its cluster is

classiﬁed to different class (label), then this data ob-

ject will be assigned to the cluster that has the nearest

objects and with the same label of it as in Eq. 4.

j =







j if cluster j ∈ C

argmin

k∈C

∑

z∈k

|cluster k|

if cluster j /∈ C

(4)

where |cluster k| is the number of objects in cluster k,

and d

is the Euclidean distance between an object z

and the labelled object x

This process continuesuntil all labelled objects within

a cluster have the same class label. Then, the process

continues to assign each unlabelled object x

to the

cluster that has the nearest labelled objects as in Eq.

5. Then, all the data objects that belong to different

clusters with the same class labels can be assigned to

that label.

j = arg min

1≤k≤N

∑

z∈k

|cluster k|

(5)

where d

is the Euclidean distance between an ob-

ject z and the unlabelled object x

This proposed method will bias clustering towards a

better search space. The proposed supervised method

is detailed in Algorithm 2. Figure 2 shows two ex-

amples; abnormal (top) and normal (bottom) images

and their results after blood vessels segmentation us-

ing NNCA, NNCA-PS, and KNN classiﬁer.

A soft classiﬁcation, where all objects are allowed

in principle to belong to all classes with different de-

grees of membership, is achieved by adding the fuzzy

memberships for each object with the clusters that be-

long to the same class label. Equations 6 and 7 show

the fuzzy membership (u

) of object x to cluster i,

and the soft membership (U

) of object x to class C

respectively.

∑

j=1





2/(q−1)

(6)

∑

if cluster j ∈ classC

(7)

where d

is the distance from object x to the current

cluster centre i (the average of all objects in cluster i),

is the distance from object x and the other cluster

centre j (1 ≤ j ≤ N

), and q is the weighting exponent

which controls the fuzziness of the resulting clusters

(q≥ 1) (Webb, 2003). A value of q = 1 gives the hard

membership, i.e. u

= 1 if x ∈ cluster i; otherwise,

= 0. In this study, q = 1.5 is used.

4 DATASETS

Two different types of real-world data are used to in-

vestigate whether the proposed algorithm scales well

with the size and dimension of the dataset.

4.1 Retinal Images

For performance evaluation, a publicly available

dataset is used (STARE, ). The dataset consists of 20

images which are digitised slides captured by a Top-

Con TRV-50 fundus camera at 35

◦

FOV. Each slide

was digitized to produce a 605×700 pixels image,

standard RGB, 8 bits per colour channel. Every im-

age has been manually segmented by two observers

to produce ground truth vessels segmentation. Ten of

these images contain pathology and the other ten are

normal, giving a good opportunity to test the proposed

method in both normal and abnormal retinas.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

328

(a) (b) (c) (d)

Figure 2: (a) Original images, (b) output from the NNCA (hard decision), (c) output from the NNCA-PS (hard decision), and

(d) output from the KNN classiﬁer (hard decision).

Algorithm 2 NNCA with partial supervision strategy

(NNCA-PS)

• Step 1: Clustering using NNCA algorithm

1. Randomly select N

points from the ground

truth to be labelled objects.

2. Cluster the N

objects into N

cluster using

NNCA clustering algorithm.

• Step 2: Apply the supervision strategy as follow:

1. Classify the clusters obtained by NNCA al-

gorithm to the class of its most labelled objects.

2. For each labelled object, if its cluster is

classiﬁed to different class (label), then this

object will be assigned to the cluster that has

the nearest objects and with the same label of it.

3. Each unlabelled object is assigned to the cluster

that has the nearest objects and then classiﬁed

to the class (label) of this cluster.

4.2 Breast Cancer Data

Two Wisconsin breast cancer datasets (UCI, ) are con-

sidered in this paper. The ﬁrst dataset contains 569

samples of 30 features each, and two classes: Benign

(class 1 and 357 samples) and Malignant (class 2 and

212 samples). The second dataset contains 683 sam-

ples of 9 features each, and two classes: Benign (class

1 and 444 samples) and Malignant (class 2 and 239

samples).

5 EXPERIMENTAL RESULTS

5.1 Retinal Images

In our experiments, retinal blood vessels are seg-

mented using the NNCA with partial supervised strat-

egy (NNCA-PS). The performance is measured by the

true and false positive rates. These rates are deﬁned

in the same way as in (Hoover et al., 2000), where

the true (false) positive is any pixel which was hand-

labelled as a vessel (not vessel), whose intensity af-

ter segmentation is above a given threshold. The true

(false) positive rate is established by the dividing the

number of true (false) positives by the total number of

pixels hand-labelled as vessels (not vessels).

For purposes of comparison, we have compared

the performance of NNCA-PS with KNN classiﬁer

(Salem and Nandi, 2006a) and RACAL with partial su-

pervision strategy (Salem et al., 2007). For the KNN

classiﬁers, two sets are required; one for training and

the other for testing, so the dataset is randomly di-

vided into two sets of images, each contains 5 nor-

mal and 5 abnormal images. The training set con-

tains large number of training samples (423500 pix-

els/image), which is huge and is the main problem

with this type of classiﬁers. To overcome such a prob-

lem, a random number of pixels are chosen from the

ﬁeld of view (FOV) of each image in the training set.

The targets for these training samples are available

from the manually segmented images. The testing

DEVELOPMENT OF A PARTIAL SUPERVISION STRATEGY TO AUGMENT A NEAREST NEIGHBOUR

CLUSTERING ALGORITHM FOR BIOMEDICAL DATA CLASSIFICATION

329

Table 1: NNCA-PS, RACAL and KNN hard decision results (average from 10 images (testing set)).

NNCA-PS RACAL (Salem et al., 2007) KNN (Salem and Nandi, 2006a)

Image type Speciﬁcity Sensitivity Speciﬁcity Sensitivity Speciﬁcity Sensitivity

% % % % % %

Normal 95.4% 90.2% 97.2% 85.9% 93.6% 88.6%

Abnormal 94.4% 87.8% 96.9% 80.3% 91.9% 82.4%

All images 94.8% 89.0% 97.0% 83.1% 92.7% 85.5%

Table 2: Average sensitivity at certain speciﬁcity values for 10 images.

NNCA-PS RACAL (Salem et al., 2007) KNN (Salem and Nandi, 2006a)

Image Speciﬁcity Sensitivity Sensitivity Sensitivity

type % % % %

Normal 90.8% 85.3% 86.6%

Abnormal 95% 86.7% 81.0% 76.2%

All images 88.8% 83.2% 81.4%

Normal 95.1% 92.9% 92.6%

Abnormal 90% 92.8% 93.5% 86.1%

All images 93.9% 93.2% 89.4%

Normal 96.9% 94.1% 95.1%

Abnormal 85% 95.4% 97.7% 90.9%

All images 96.1% 95.9% 92.9%

Normal 98.1% 98.1% 96.5%

Abnormal 80% 96.9% 96.6% 93.7%

All images 97.5% 97.4% 95.1%

set contains 10 images to test the performance of the

classiﬁer. The value of K = 60 and each feature is

normalised to zero mean and unit standard deviation.

While for NNCA-PS and RACAL with partial supervi-

sion strategy, only 30% of all the pixels are known (as

vessels or non-vessels pixels) to demonstrate the ad-

vantage of using a small proportion of labelled pixels

in clustering the unlabelled pixels.

For hard classiﬁcation, the same set of images is

used when comparing with the KNN classiﬁer. As

shown in Table 1, NNCA-PS achieves average sensi-

tivity (true positive rate) of 89% at average speciﬁcity

(1-false positive rate) of 94.8%, while the KNN clas-

siﬁer achieves sensitivity of 85.5% at average speci-

ﬁcity of 92.7%. On average, the proposed NNCA-PS

achieves better speciﬁcity as well as sensitivity than

KNN classiﬁer. On average, RACAL (Salem et al.,

2007) achieves 2% higher speciﬁcity than NNCA-PS,

but it offers 6% less sensitivity than NNCA-PS.

For soft classiﬁcation as shown in Table 2, the soft

classiﬁcation results of the proposed NNCA-PS are

compared with the soft results of RACAL and KNN.

As shown, at 95% speciﬁcity, the proposed NNCA-

PS achieves 5.5% and 4.2% higher sensitivity than

RACAL and KNN respectively in case of normal im-

ages. Also in abnormal images at 95% speciﬁcity,

NNCA-PS achieves 5.7% and 10.5% higher sensitiv-

ity than RACAL and KNN respectively. For higher

speciﬁcity, KNN classiﬁer achieves the lowest aver-

age sensitivity compared with NNCA-PS and RACAL,

while both NNCA-PS and RACAL achieves on aver-

age comparable sensitivity.

5.2 Breast Cancer Datasets

For purposes of comparison, a series of experiments

were carried out to examine the performance of

NNCA when applying the proposed supervision strat-

egy (NNCA-PS) on breast cancer datasets, where the

classiﬁcation results obtained by NNCA with the su-

pervision strategy on breast cancer dataset 1 are com-

pared with the results (Guo and Nandi, 2006) of dif-

ferent classiﬁers (PCA/MDC “Principal Component

Analysis / Minimum Distance Classiﬁer” (Theodor-

idis and Koutroubas, 2003; Cios et al., 1998),

FLDA/MDC “Fisher Linear Discriminant Analysis /

MDC” (Cios et al., 1998), MLP “Multi-Layer Per-

cepton“ (Duha et al., 2001), SVM “Support Vector

Machine” (Hsu and Lin, 2002), and GP/MDC “Ge-

netic Programming/ MDC” (Guo and Nandi, 2006;

Kishore et al., 2002)). In order to achieve fair com-

parisons as in (Guo and Nandi, 2006), we randomly

selected, without replacement, 100 samples (from the

entire dataset) for training, and 100 samples for test-

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

330

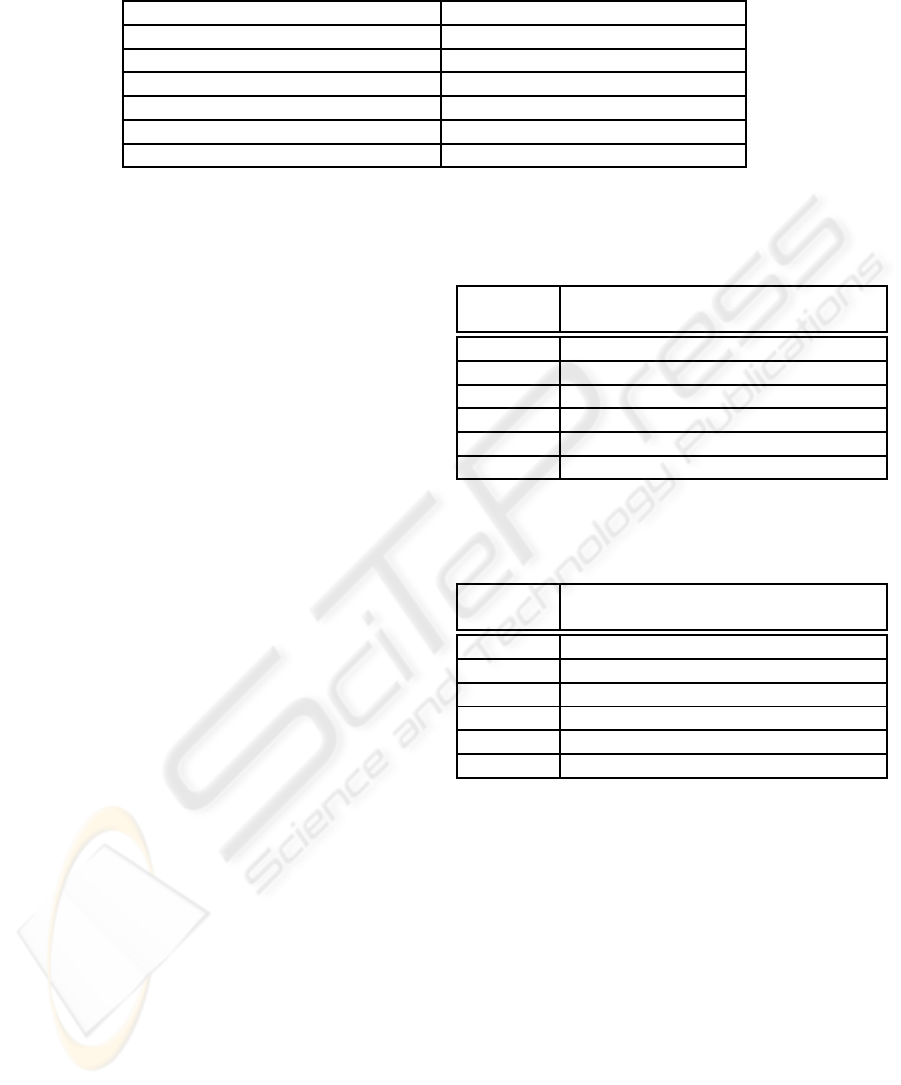
Table 3: Comparison of classiﬁcation accuracy (%) for breast cancer dataset 1 (testing set) using NNCA-PS and different

classiﬁers, based on 100 experiments.

Algorithms Best (%) Average (%) Std (%)

PCA/MDC (Guo and Nandi, 2006) 88.7 88.6 N/A

FLDA/MDC (Guo and Nandi, 2006) 88.9 88.6 N/A

MLP (Guo and Nandi, 2006) 97.3 96.2 1.7

SVM (Guo and Nandi, 2006) 96.7 96.3 0.8

GP/MDC (Guo and Nandi, 2006) 98.9 97.4 1.5

NNCA-PS 99.5 97.2 1.2

ing; this process has been repeated 100 times. The tar-

get information, class labels, of the training samples

is used to guide the clustering process of the testing

samples using NNCA-PS algorithm. Table 3 shows

comparison results of NNCA-PS along with different

methods for classiﬁcation. As shown, the best clas-

siﬁcation accuracy is achieved by NNCA-PS (99.5%),

with the lowest being 88.7% obtained by PCA/MDC

which gives comparable results as FLDA/MDC. Al-

though the average classiﬁcation accuracy obtained

by GP/MDC are comparable with NNCA-PS, it gives

0.6% less than the best performance of NNCA-PS

with higher standard deviation in classiﬁcation accu-

racy. Therefore, the proposed method is more robust

compared with other methods.

In order to reduce the amount of a priori knowl-

edge, a small number of objects from the entire

dataset are used as labelled objects. In these exper-

iments, the effect of the number of labelled objects on

the classiﬁcation accuracy are investigated. We ran-

domly selected a fraction from the entire dataset to be

labelled objects. For each fraction, this process is re-

peated one hundred times without replacement. The

best, average, and standard deviation of classiﬁcation

accuracy are obtained over one hundred runs for each

fraction of labelled objects. For breast cancer dataset

1, as demonstrated in Table 4, the best and average

classiﬁcation accuracies increase with the increas-

ing fraction of the labelled objects. As shown, the

best and average classiﬁcation accuracy of 98.2% and

96.3% respectively were achievedat 30% labelled ob-

jects, with the lowest being 96.2% and 91.5% for best

and average accuracies respectively at 5% labelled

objects. By examining the average and standard de-

viation of the classiﬁcation performance, when 5%

of the entire dataset are labelled, the average perfor-

mance is the lowest, while it has the highest standard

deviation compared with the other fractions of la-

belled objects. For breast cancer dataset 2 as recorded

in Table 5, the standard deviations is lower than the

standard deviations of breast cancer dataset 1. It is

conjectured that the clusters on breast cancer dataset

2 are more compact with those in breast cancer dataset

Table 4: Classiﬁcation accuracy (%) for breast cancer

dataset 1 (entire dataset) using NNCA with partial super-

vision (NNCA-PS), based on 100 experiments.

labelled

objects % Best (%) Average (%) Std (%)

5 96.2 91.5 2.3

10 96.3 93.1 1.8

15 97.0 94.4 1.3

20 97.2 95.3 1.0

25 97.6 95.6 0.9

30 98.2 96.3 0.7

Table 5: Classiﬁcation accuracy (%) for breast cancer

dataset 2 (entire dataset) using NNCA with partial super-

vision (NNCA-PS), based on 100 experiments.

labelled

objects % Best (%) Average (%) Std (%)

5 98.0 96.0 1.2

10 98.1 96.3 1.1

15 98.5 96.7 0.9

20 98.7 97.0 0.8

25 98.7 97.4 0.7

30 99.2 97.9 0.5

1, as indicated in (Salem and Nandi, 2005). For 5%

labelled objects and higher, the best classiﬁcation ac-

curacy is higher than 98% with a small decrease in the

standard deviation and a signiﬁcant increase in the av-

erage classiﬁcation accuracy as demonstrated in Table

When comparing the proposed NNCA-PS with

RACAL for breast cancer data classiﬁcation, where

a small number of objects from the entire dataset

are used as labelled objects. The average classi-

ﬁcation accuracy for breast cancer dataset 1 using

NNCA-PS is 1% higher than RACAL algorithm while

it achieves comparable accuracy for breast cancer

dataset 2 as demonstrated in Tables 6 and 7. More-

over, the standard deviation of the classiﬁcation per-

formance of NNCA-PS for breast cancer dataset 1 is

lower than RACAL which favors compact clusters,

DEVELOPMENT OF A PARTIAL SUPERVISION STRATEGY TO AUGMENT A NEAREST NEIGHBOUR

CLUSTERING ALGORITHM FOR BIOMEDICAL DATA CLASSIFICATION

331

Table 6: Comparison of classiﬁcation accuracy (%) for breast cancer dataset 1 (entire dataset) using NNCA and RACAL with

partial supervisions, based on 100 experiments.

NNCA-PS RACAL

labelled (Salem and Nandi, 2006b)

objects % Average(%) ± Std(%) Average(%) ± Std(%)

5 91.5 ± 2.3 90.6 ± 4.7

10 93.1 ± 1.8 92.1 ± 3.2

15 94.4 ± 1.3 93.5 ± 2.3

20 95.3 ± 1.0 94.4 ± 1.8

25 95.6 ± 0.9 94.9 ± 1.6

30 96.3 ± 0.7 95.2 ± 1.7

Table 7: Comparison of classiﬁcation accuracy (%) for breast cancer dataset 2 (entire dataset) using NNCA and RACAL with

partial supervisions, based on 100 experiments.

NNCA-PS RACAL

labelled (Salem and Nandi, 2006b)

objects % Average(%) ± Std(%) Average(%) ± Std(%)

5 98.0 ± 1.2 97.5 ± 1.4

10 98.1 ± 1.1 97.9 ± 0.3

15 98.5 ± 0.9 98.2 ± 0.3

20 98.7 ± 0.8 98.6 ± 0.3

25 98.7 ± 0.7 98.6 ± 0.3

30 99.2 ± 0.5 98.6 ± 0.3

while it achieves slightly higher standard deviations

in breast cancer dataset 2. This may be the result of

the NNCA-PS achieving clustering without any con-

trol of cluster sizes while RACAL is constrained with

a radius parameter δ

which controls the size of the

clusters.

6 CONCLUSIONS

In this paper, we have proposed a partial supervision

strategy for a recently developed clustering algorithm

(NNCA) to act as a classiﬁer. We examined its appli-

cability and reliability using datasets from real-world

problems. As shown, the proposed NNCA-PS has the

ability to classify pixels of retinal images into those

belonging to blood vessels and others not belonging

to blood vessels, and it also has the ability to classify

breast tumors into either benign or malignant. Ex-

perimental results show that the proposed algorithm

offers better classiﬁcation accuracies compared with

certain other classiﬁers.

REFERENCES

Bouchachia, A. and Pedrycz, W. (2006). Data clustering

with partial supervision. Data Mining and Knowledge

Discovery, 12:47–78.

Cios, K., Pedrycz, W., and Swiniarski, R. (1998). Data

Mining Methods for Knowledge Discovery. Kluwer

Academic, Boston.

Doi, K. (2005). Current status and future potential of

computer-aided diagnosis in medical imaging. The

British Journal of Radiology, 78:3–19.

Duha, R., Hart, P., and Stork, D. (2001). Pattern Classiﬁca-

tion. John Willey & Sons, Inc., Chichester.

Guo, H. and Nandi, A. (2006). Breast cancer diagnosis us-

ing genetic programming generated feature. Pattern

Recognition, 39(5):980–987.

Hoover, A., Kouznetsova, V., and Goldbaum, M. (2000).

Locating blood vessels in retinal images by piecewise

thresholding probing of a matched ﬁlter response.

IEEE Transaction on Medical Imaging, 19:203–210.

Hsu, C. and Lin, C. (2002). A comparison of methods for

multiclass support vector machines. IEEE Transac-

tions on Neural Networks, 13:415–425.

Jain, A. and Dubes, R. (1988). Algorithms for Clustering

Data. Prentice Hall.

Jain, A., Murty, M., and Flyn, P. (1999). Data clustering: A

review. ACM Computing Surveys, 31(3):264–323.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

332

Kishore, J., Patnaik, L., Mani, V., and Arawal, V. (2002).

Application of genetic programming for multicate-

gory pattern classiﬁcation. IEEE Transaction on

Evoluationary Computation, 4:242–258.

Salem, N. and Nandi, A. (2006a). Segmentation of retinal

blood vessels using scale space features and k-nearest

neighbour classiﬁer. In The 31st International Con-

ference on Acoustics, Speech, and Signal Processing

(ICASSP 2006), Toulouse, France.

Salem, S. and Nandi, A. (2005). New assessment crite-

ria for clustering algorithms. In IEEE international

workshop in Machine Learning For Signal Processing

(MLSP 2005), pages 285–290, Mystic, CT, USA.

Salem, S. and Nandi, A. (2006b). Novel clustering algo-

rithm (RACAL) and a partial supervision strategy for

classiﬁcation. In IEEE international workshop in Ma-

chine Learning For Signal Processing (MLSP 2006),

pages 313–318, Mynooth, Ireland.

Salem, S., Salem, N., and Nandi, A. (2006). Segmenta-

tion of retinal blood vessels using a novel clustering

algorithm. In 14th European Signal Processing Con-

ference (EUSIPCO 2006), Florence, Italy.

Salem, S., Salem, N., and Nandi, A. (2007). Segmenta-

tion of retinal blood vessels using a novel clustering

algorithm (RACAL) with a partial supervision strat-

egy. Medical and Biological Engineering and Com-

puting, 45(3):261–273.

Theodoridis, S. and Koutroubas, K. (2003). Pattern Recog-

nition. Academic Press, San Diego.

STARE. The STARE project.

http://www.ces.clemson.edu/ ahoover/stare.

UCI. UCI repository of machine learning databases.

http://www.ics.uci.edu/ mlearn/MLRepository.html.

Webb, A. (2003). Statistical Pattern Recognition. John Wil-

ley & Sons, Inc.

Xu, R. and Wunsch, D. (2005). Survey of clustering al-

gorithms. IEEE Transactions on Neural Networks,

16(3):645–677.

DEVELOPMENT OF A PARTIAL SUPERVISION STRATEGY TO AUGMENT A NEAREST NEIGHBOUR

CLUSTERING ALGORITHM FOR BIOMEDICAL DATA CLASSIFICATION

333