BIOSIGNAL-BASED COMPUTING BY AHL INDUCED SYNTHETIC
GENE REGULATORY NETWORKS
From an in vivo Flip-Flop Implementation to Programmable Computing Agents
T. Hinze, T. Lenser, N. Matsumaru, P. Dittrich
Bio Systems Analysis Group, Friedrich-Schiller-Universit¨at Jena, Ernst-Abbe-Platz 1–4, D-07743 Jena, Germany
S. Hayat
Computational Biology Group, Universit¨at des Saarlandes, Im Stadtwald, PF 15 11 50, D-66041 Saarbr¨ucken, Germany
Keywords:
Biologically inspired computing, gene regulatory networks, bistable toggle switch, NP complete problem.
Abstract:
Gene regulatory networks (GRNs) form naturally predefined and optimised computational units envisioned
to act as biohardware able to solve hard computational problems efficiently. This interplay of GRNs via sig-
nalling pathways allows the consideration as well as implementation of interconnection-free and fault tolerant
programmable computing agents. It has been quantitatively shown in an in vivo study that a reporter gene
encoding the green fluorescent protein (gfp) can be switched between high and low expression states, thus
mimicking a NAND gate and a RS flip-flop. This was accomplished by incorporating the N-acyl homoserine
lactone (AHL) sensing lux operon from Vibrio fischeri along with a toggle switch in Escherichia coli. gfp
expression was quantified using flow cytometry. The computational capacity of this approach is extendable
by coupling several logic gates and flip-flops. We demonstrate its feasibility by designing a finite automaton
capable of solving a knapsack problem instance.
1 INTRODUCTION
Molecular biosignals of GRNs are suited for comput-
ing purposes. Beyond error-prone molecular comput-
ers in vitro, the idea of computing in vivo becomes
more and more attractive (Kobayashi et al., 2004;
Weiss et al., 1999). Motivated by the presence of nat-
urally predefined functional units found in microor-
ganisms, their exploration towards computing agents
seems promising. GRNs can be viewed as computa-
tional devices of pro- and eukaryotic cells, triggering
and directing responses to external inputs influenced
by genetically stored information. Emerged from an
evolutionary optimisation, they form reliable modu-
larised systems with obvious advantages in carrying
out massively parallel calculations.
Recently, more than 6, 000 transcription factors
acting as signal inducers or transmitters in GRNs
have been listed in the public Transpath and Trans-
fac database. Selection of GRN candidates in con-
cert with their ability for composition via specific
receptor-controlled interfaces is of particular interest
for creating computing agents. Following the pio-
neering implementation of a bistable toggle switch
in vivo (Gardner et al., 2000), we could confirm
its practicability in a previous study (Hayat et al.,
2006). Two extensions in the experimental setup
were investigated: Firstly, the effects of isopropyl-β-
D-thiogalactopyranoside (IPTG) and AHL as appro-
priate intercellular inducers for flip-flop setting were
shown. Secondly, flow cytometry was used to quan-
titatively measure protein concentrations within the
flip-flop implementation. Section 3 briefly explains
underlying methods and materials, while section 4
describes the experiment. Based on these experi-
mental results, we identify GRNs able to function
as NAND gates and RS flip-flops (section 5). For
these computational units, we present a homogeneous
dynamical model using Hill kinetics (Mestl et al.,
1995). Unit composition is exemplified by design of
a finite automaton for a knapsack problem instance
(section 6). We transfer this automaton into a min-
imised logic circuit consisting of interacting NAND
gates. A subsequent simulation of the correspond-
ing computing agent on the GRN level demonstrates a
constructive approach towards programmable in vivo
computers encouraged by the Turing completeness of
(bio)chemical reaction networks (Magnasco, 1997).
162
Hinze T., Lenser T., Matsumaru N., Dittrich P. and Hayat S. (2008).
BIOSIGNAL-BASED COMPUTING BY AHL INDUCED SYNTHETIC GENE REGULATORY NETWORKS - From an in vivo Flip-Flop Implementation to
Programmable Computing Agents.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 162-169
DOI: 10.5220/0001056701620169
Copyright
c
 SciTePress

2 RELATED WORK
First ideas about principles of interconnection-free
biomolecular computation were introduced in (Aoki
et al., 1992; Thomas, 1991). Along with the growing
knowledge in genetics and proteomics, the imagina-
tion of computing in vivo came into the focus of scien-
tific research (Weiss et al., 1999). Several approaches
address engineering of GRNs using predefined net-
work motifs (Guido et al., 2006; Kaern et al., 2003;
Kobayashi et al., 2004). Inspired by advantageous
properties of specific GRNs for computational tasks,
construction and implementation of genetic circuits
has been successfully explored (Gardner et al., 2000;
Sprinzak and Elowitz, 2005; Yokobayashi et al.,
2004). Recently, these circuits have been used to form
logic gates, clocks (oscillators), switches, or sensors.
As a next step, their combination to achieve higher
integrated problem-specific designs will be investi-
gated. A DNA-based solution to the knapsack prob-
lem in vitro was introduced in (Hinze et al., 2002).
An alternative approach in vivo generates a variety
of encoding plasmids that are translated into proteins
(Henkel et al., 2007).
3 BIOLOGICAL PRINCIPLES
AND PREREQUISITES
3.1 Quorum Sensing and Autoinduction
via AHL
In quorum sensing, bacterial species regulate gene ex-
pression based on cell-population density (Miller and
Bassler, 2001). An alteration in gene expression oc-
curs when an intercellular signalling molecule termed
autoinducer, produced and released by the bacterial
cells reaches a critical concentration. Termed as quo-
rum sensing or autoinduction, this fluctuation in au-
toinducer concentration is a function of bacterial cell-
population density. Vibrio fischeri, a well studied
bacterium, colonises the light organs of a variety of
marine fishes and squids, where it occurs at very
high densities (10
10
cells
ml
) and produces light. The two
genes essential for cell density regulation of lumines-
cence are: luxI, which codes for an autoinducer syn-
thase (Schaefer et al., 1996); and luxR, which codes
for an autoinducer-dependent activator of the lumi-
nescence genes. The luxR and luxI genes are adjacent
and divergently transcribed, and luxI is the first of
seven genes in the luminescence or lux operon. LuxI-
type proteins direct AHL synthesis while LuxR-type
proteins function as transcriptional regulators that are
capable of binding AHL signal molecules. Once
formed, LuxR-AHL complexes bind to target pro-
moters of quorum-regulated genes. Quorum sensing
is now known to be widespread among both Gram-
positive and Gram-negative bacteria.
3.2 Bioluminescence in Vibrio fischeri
Bioluminescence in general is defined as an enzyme
catalysed chemical reaction in which the energy re-
leased is used to produce an intermediate or product
in an electronically excited state, which then emits
a photon. It differs from fluorescence or phospho-
rescence as it is not depended on light absorbed.
The mechanism for gene expression and the struc-
ture of the polycistronic message of the lux structural
genes in Vibrio fischeri have been thoroughly charac-
terised (Hastings and Nealson, 1977). Briefly, there
are two substrates, luciferin, which is a reduced flavin
mononucleotide (FMNH
2
), and a long chain (7 − 16
carbons) fatty aldehyde (RCHO). An external re-
ductant acts via flavin mono-oxygenase oxidoreduc-
tase to catalyse the reduction of FMN to FMNH
2
,
which binds to the enzyme and reacts with O
2
to
form a 4a-peroxy-flavin intermediate. This com-
plex oxidises the aldehyde to form the correspond-
ing acid (RCOOH) and a highly stable luciferase-
hydroxyflavin intermediate in its excited state, which
decays slowly to its ground state emitting blue-green
light hν with a maximum intensity at about 490nm:
FMNH
2
+ RCHO+ O
2
lucif.
−→
FMN+ H
2
O+ RCOOH+ hν
(1)
3.3 Transcription Control by LacR and
λCI Repressor Proteins
Escherichia coli cells repress the expression of the
lac operon when glucose is abundant in the growth
medium. Only when the glucose level is low and the
lactose level is high, the operon is fully expressed.
The Lac repressor LacR is a 360 residue long pro-
tein that associates into a homotetramer. It contains
a helix-turn-helix (HTH) motif through which it in-
teracts with DNA. This interaction represses tran-
scription by hindering association with RNA poly-
merase and represents an example of “combinatorial
control” widely seen in prokaryotes and eukaryotes
(Buchler et al., 2003). The CI repressor of bacterio-
phage lambda is the key regulator in lambda’s genetic
switch, a bistable switch that underlies the phage’s
ability to efficiently use its two modes of development
(Ptashne, 1992).
BIOSIGNAL-BASED COMPUTING BY AHL INDUCED SYNTHETIC GENE REGULATORY NETWORKS - From an
in vivo Flip-Flop Implementation to Programmable Computing Agents
163

3.4 Flow Cytometry
Flow cytometry refers to the technique where micro-
scopic particles are counted and examined as they
pass in a hydro-dynamically focused fluid stream
through a measuring point surrounded by an array of
detectors. Previously, flow cytometry analyses were
performed by us using a BD LSRII flow cytome-
ter equipped with 405nm, 488nm and 633nm lasers.
488nm laser was used for gfp and yellow fluorescent
protein (yfp) quantification.
4 IMPLEMENTATION OF A
COMPUTATIONAL UNIT IN
VIVO
4.1 Experimental Setup
We have shown that an in vivo system (Hayat et al.,
2006) can potentially be used to mimic a RS flip-flop
(Huffman, 1954; Morris Mano, 1991) and have quan-
tified its performance using flow cytometry. The pres-
ence or absence of the inducers IPTG or AHL in com-
bination with temperature shift acts as an input sig-
nal. The toggle switch comprising of structural genes
for reporter/output proteins fused to promoter regions
that are regulated by input signals is visualised as a
RS flip-flop, see figure 1. The functional modularity
of the input and output circuits is maintained so that
the artificial GRN used can be easily extended for fu-
ture studies.
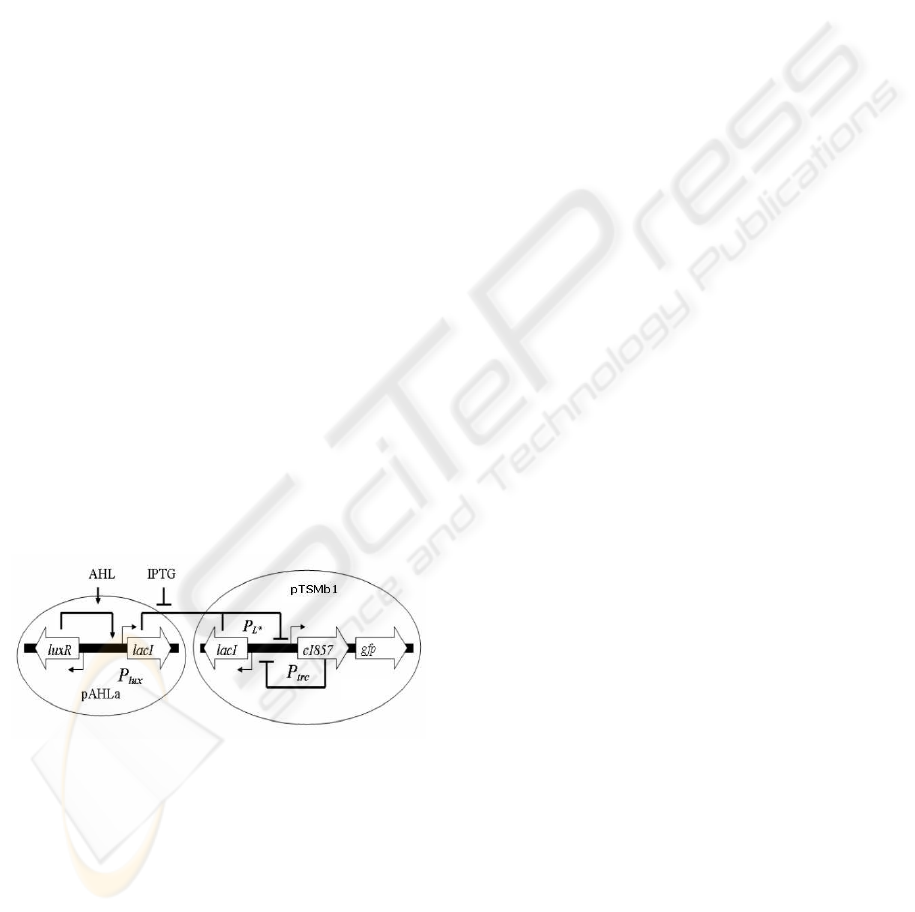
Figure 1: A schematic diagram of an AHL biosensor mod-
ule interfaced with the genetic toggle switch adapted from
(Hayat et al., 2006). The transgenic artificial GRN consists
of a bistable genetic toggle switch (Gardner et al., 2000)
which is interfaced with genes from the lux operon (En-
gebrecht and Silverman, 1984) of the quorum sensing sig-
nalling pathway of Vibrio fischeri (Schaefer et al., 1996).
This design endows cells with two distinct pheno-
typic states: where the λCI activity is high and the ex-
pression of lacI is low (referred to as high or 1 state),
or where the activity of LacR is high and the expres-
sion of λCI is low (referred to as low or 0 state). gfp is
expressed only in the high λCI/low LacR state. Fig-
ure 2 shows the experimental results obtained by flow
cytometry.
4.2 Results and Discussion
For co-relational purposes, all experiments were con-
ducted with both BL21 and Top10 strains of Es-
cherichia coli. The concentration of IPTG used in all
the experiments was 2mM and that of AHL was 1µM.
Experiments conducted without the use of inducers,
lead to an unreliable shifting of the states, signify-
ing the use if inducers in a tightly, mutually regulated
circuit. Further experiments conducted to understand
the switching dynamics of the circuit revealed that in
the current scenario, it was easier to switch from a
high to a low state than vice versa. This discrepancy
in switching behaviour is attributed to the differing
modes of elimination of LacR and λCI repressor pro-
teins. While switching from low to high state, the re-
pression due to IPTG-bound Lac repressor needs to be
overcome by cell growth. Switching from high to low
state is effected by immediate thermal degradation of
the temperature-sensitive λCI. Experiments were also
conducted to test the sustainability of states. The plug
and play property of the circuit was examined by em-
ploying yfp as the reporter gene instead of gfp. As
shown in figure 2, the circuit could reliably mimic a
RS flip-flop. The massive parallelism permissible by
the use of large quantities of cells can compensate for
the slow speed of switching. Further tests are to be
performed to confirm this hypothesis.
5 DEFINITION OF
COMPUTATIONAL UNITS
Artificial GRNs have been instrumental in elucidating
basic principles that govern the dynamics and conse-
quences of stochasticity in the gene expression of nat-
urally occurring GRNs. The realisation as computa-
tional circuits infers inherent evolutionary fault toler-
ance and robustness to these modular units.
In a more abstract view, generalised building
blocks adopted from previous in vivo studies can be
identified. In terms of predefined GRN modules, they
form computational units. We introduce two artifi-
cial GRNs for logic gates and describe their dynam-
ical behaviour quantitatively by an ordinary differen-
tial equation model using Hill kinetics (Mestl et al.,
1995). A variety of specific signalling proteins (tran-
scription factors) given by their concentration over
the time course enables communication between as
well as coupling of computational units. Thus, circuit
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
164

A
B
0
5.000
10.000
15.000
0
5.000
10.000
30.000
GFP mean:
14.803 units
GFP mean:
4.856 units
GFP mean:
1.108 units
GFP mean:
601 units
GFP mean:
15.621 units
GFP mean:
7.073 units
after 12 hrs after 24 hrs after 36 hrs after 48 hrs after 60 hrs after 72 hrs
12 24 36 48 60 720
0
1
0
1
30°C42°C
GFP mean (average units) Flip−flop output Setting
IPTG,
Resetting AHL,
Set Reset Set
Store Store Store
low (0)
high (1)
time (hrs)
12 24 36 48 60 720
0
1
0
1
30°C42°C
GFP mean (average units) Flip−flop output Setting
IPTG,
Resetting AHL,
Reset Set Reset
Store Store Store
low (0)
high (1)
time (hrs)
GFP mean:
188 units
after 12 hrs
GFP mean:
312 units
after 24 hrs
GFP mean:
32.178 units
after 36 hrs
GFP mean:
4.106 units
after 48 hrs
644 units
GFP mean:
after 60 hrs
GFP mean:
373 units
after 72 hrs
Figure 2: Inducer-dependent switching. Repeated activation and deactivation of the toggle switch based on inducers and
temperature. Temperature was switched every 24 hours. Cells were incubated with inducers for 12 hours, followed by growth
for 12 hours without inducers, initially kept at 30
◦
C (A) and 42
◦
C (B). The cells successfully switched states thrice.
engineering becomes feasible. Resulting computing
agents can serve as templates for experimental setups.
We distinguish computationalunits within a circuit by
index i.
Hill kinetics represents a homogeneous approach
to model cooperativeand competitive aspects of inter-
acting biochemical reaction networks. It formulates
the relative intensity of gene regulations by sigmoid-
shaped threshold functions h of degree m and thresh-
old Θ > 0 such that x ≥ 0 specifies the concentration
level of a transcription factor that activates resp. in-
hibits gene expression. Function value h then returns
the normalised change in concentration level of the
corresponding gene product. It reaches a concentra-
tion level of 50% iff x = Θ.
Activation (upregulation) →:
h
+
(x, Θ,m) =
x
m
x
m
+ Θ
m
(2)
Inhibition (downregulation) ⊥:
h
−
(x, Θ,m) = 1 − h
+
(x, Θ,m) (3)
5.1 NAND Gate
Input: concentration levels of transcription factors
x
i
, y
i
Output: concentration level of gene product z
i
The dynamical system behaviour is defined by ordi-
nary differential equations 4, 5, and 6.
˙a
i
= h
+
(x
i
, Θ
i1
, m
i1
) − a
i
(4)
˙
b
i
= h
+
(y
i
, Θ
i2
, m
i2
) − b
i
(5)
˙z
i
= 1− h
+
(a
i
, Θ
i3
, m
i3
) · h
+
(b
i
, Θ
i4
, m
i4
)
−z
i
(6)
BIOSIGNAL-BASED COMPUTING BY AHL INDUCED SYNTHETIC GENE REGULATORY NETWORKS - From an
in vivo Flip-Flop Implementation to Programmable Computing Agents
165

z
i
y
i
x
i
a
i b
i
y
i
x
i
z
i
x
i
y
i
z
i
0
1
0
0
10
1 1
1
1
1
0
&
0
0.2
0.4
0.6
0.8
1
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40
Normalised concentration
Time scale
Input1: 1
Input2: 0
Input1: 1
Input2: 1
Input1: 0
Input2: 1
Input1: 0
Input2: 0
Output
NAND gate i
effector gene iregulator gene y iregulator gene x i
complex formation
Figure 3: GRN mimicking a NAND gate. Dynamical be-
haviour shown for m
ij
= 2, Θ
ij
= 0.1, j = 1, . . . , 4, a(0) = 0,
b(0) = 0, z(0) = 0 (Copasi ODE solver simulation).
5.2 RS Flip-Flop
Input: concentration levels of transcription factors
S
i
, R
i
Output: concentration level of gene product Q
i
The dynamical system behaviour is defined by ordi-
nary differential equations 7, 8, and 9.
˙a
i
= 1− h
+
(b
i
, Θ
i1
, m
i1
) · h
−
(S
i
, Θ
i2
, m
i2
)
−a
i
(7)
˙
b
i
= 1− h
+
(a
i
, Θ
i3
, m
i3
) · h
−
(R
i
, Θ
i4
, m
i4
)
−b
i
(8)
˙
Q
i
= h
+
(b
i
, Θ
i1
, m
i1
) · h
−
(S
i
, Θ
i2
, m
i2
)
−Q
i
(9)
Q
i
R
i
S
i
b
i
a
i
S
i
R
i
Q
i
R
i
S
i
Q
i
0
0
1
1
1
0
0
0
1
1
hold
−
&
&
0
0.2
0.4
0.6
0.8
1
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40
Normalised concentration
Time scale
Set
-S: 0, -R: 1
Store
-S: 0, -R: 0
Reset
-S: 1, -R: 0
Store
-S: 0, -R: 0
Output
low active RS flip−flop i
effector gene iregulator gene set state iregulator gene reset state i
Figure 4: GRN mimicking a low active RS flip-flop. Dy-
namical behaviour shown for m
ij
= 2, Θ
ij
= 0.1, j =
1, . . . , 4, a(0) = 0, b(0) = 0, Q(0) = 0 (Copasi ODE solver
simulation).
A homologous model of a bistable toggle switch was
introducedin (Gardner et al., 2000). In case of the for-
bidden input signalling S
i
= 1, R
i
= 1, the normalised
concentrations of both proteins a
i
and b
i
converge to
0.5. By setting or resetting input signalling, the flip-
flop restores.
6 AN ARTIFICIAL GRN FOR
KNAPSACK PROBLEM
SOLUTION
We demonstrate the feasibility of unit composition
for solution of more complex problems, exemplified
by the integer knapsack problem. It is known to be
NP complete, defined by n natural numbers a
1
, . . . , a
n
representingweights of correspondingobjects 1, . . . , n
and a reference weight b given by a natural number.
Is there a subset I ⊆ {1, . . . , n} such that
∑
i∈I
a
i
= b ?
Brute force approaches enumerating the whole search
space consider up to 2
n
solution candidates.
Regarding a reaction network-based algorithm,
the dynamic programming approach introduced in
(Baum and Boneh, 1999) provides an appropriate
framework to be adapted for our purpose. Here, the
problem parameters are encoded into a directed graph
G = (V, E) with a (b + 1) × (n + 1) grid of nodes
V = {v
(i,k)
| ∀i = 0, . . . , b ∀k = 0, . . . , n} and edges
E ⊂ V × V as follows: E = {

v
(i,k)
, v
(i,k+1)

| ∀i =
0, . . . , b ∀k = 0, . . . , n−1}∪{

v
(i,k)
, v
(i+a
i
,k+1)

| ∀i =
0, . . . , b : i + a
i
≤ b ∀k = 0, . . . , n − 1}. The answer
to the knapsack problem is yes iff there exists a path
through G from v
(0,0)
to v
(b,n)
.
As an example for GRN network composition,
we choose the problem instance n = 3, a
1
= 3, a
2
=
1, a
3
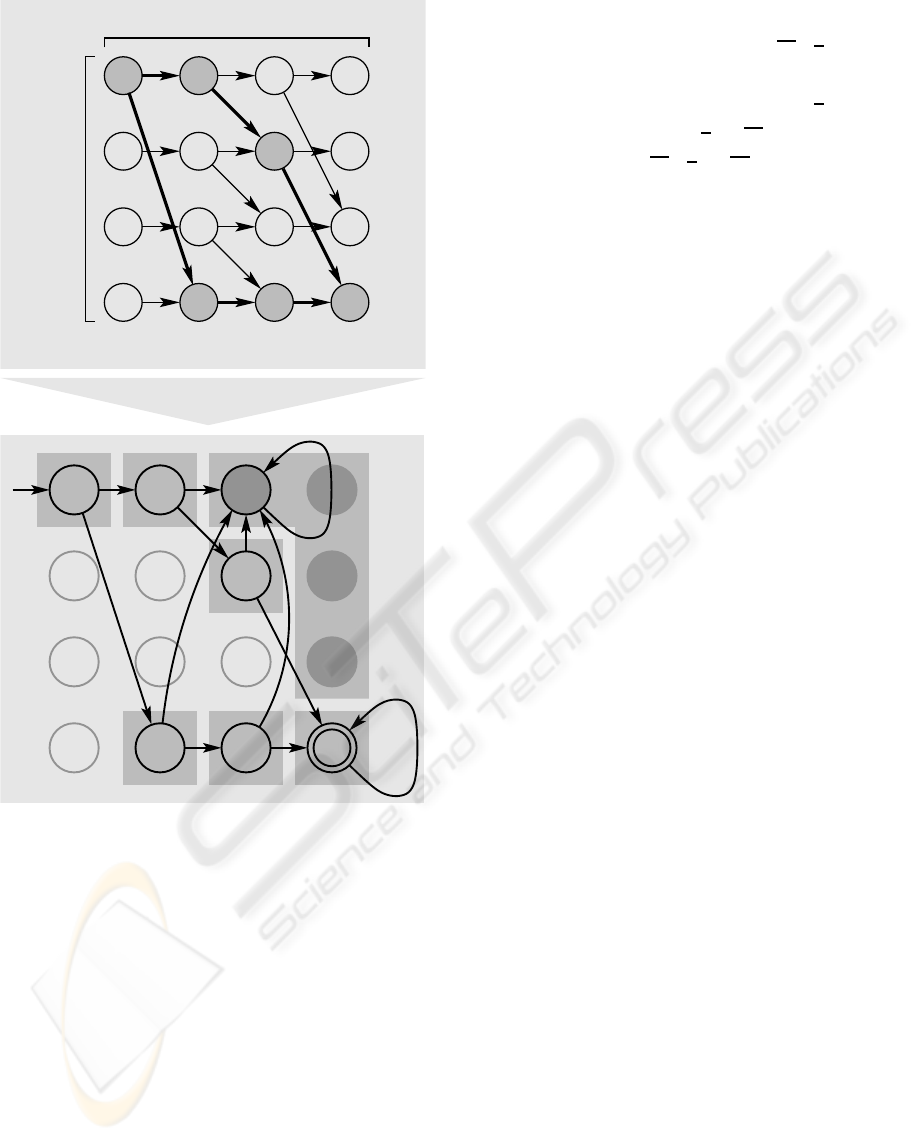
= 2, b = 3. Upper part of figure 5 illustrates
graph G in this case. Having in mind the presence
of a separate signal generator module, we can in-
terpret G as a finite automaton. Assume that the
generator module continually disseminates transmit-
ter substances representing binary strings. Computing
agents are able to receive these substances in parallel.
So, one agent randomly obtains one binary string for
subsequent processing in terms of input data. Act-
ing as a (finite) automaton, the agent can reach a final
state which is coupled to the expression of gfp.
In this example, the agent checks whether or not
the binary string as a candidate solution meets the an-
swer “yes”. Therefore, the first three input bits are
interpreted as presence (1) or absence (0) of an object
corresponding to the bit position. Accordingly, binary
strings 011 and 100 lead to the positive answer. In or-
der to construct the finite automaton from grid G , we
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
166

111101100
010
011
110
0 0
0
00
yes
1 1
1
1
1
0,1
no
0,100
*
a
1
= 3
a
2
= 1
a
3
= 2
v
n+1
b+1 nodes
nodes
v
(0,0)
(b,n)
Figure 5: Construction of a deterministic finite automaton
(lower part) from the dynamic programming approach (up-
per part).
transform the nodes into states whereas v
(0,0)
is the
initial and v
(b,n)
the final state. Unreachable states are
removed, and all four states that yield the answer “no”
are subsumed into one, see lower part of figure 5. Fi-
nally, we obtain seven states. For preparation of the
NAND-based network as template for GRN composi-
tion, we term each state by a three bit binary number
b
1
b
2
b
3
. With regard to a minimal number of NAND
gates in the final circuit, the Gray code schema is used
for state numbering. So, each transition flips at most
one bit. Additionally, one state may carry a one-bit
don’t-care term marked by ∗ that arbitrarily embod-
ies 1 or 0. Using Karnaugh optimisation, the binary
number b
′
1
b
′
2
b
′
3
for the new state based on the previ-
ous state b
1
b
2
b
3
and the input bit x is defined by:
b
′
1
= (b
1
∧ b
2
∧ b
3
) ∨ (b
1
∧ b
2
∧ x)
∨(b
2
∧ b
3
∧ x) ∨ (b
1
∧ b
2
∧ x) (10)
b
′
2
= (b
1
∧ b
2
∧ b
3
) ∨ (b
1
∧ b
2
∧ x)
∨(b
1
∧ b
3
∧ x) ∨ (b
1
∧ b
2
∧ x) (11)
b
′
3
= b
3
∨ (b
2
∧ x) ∨ (b
1
∧ x) (12)
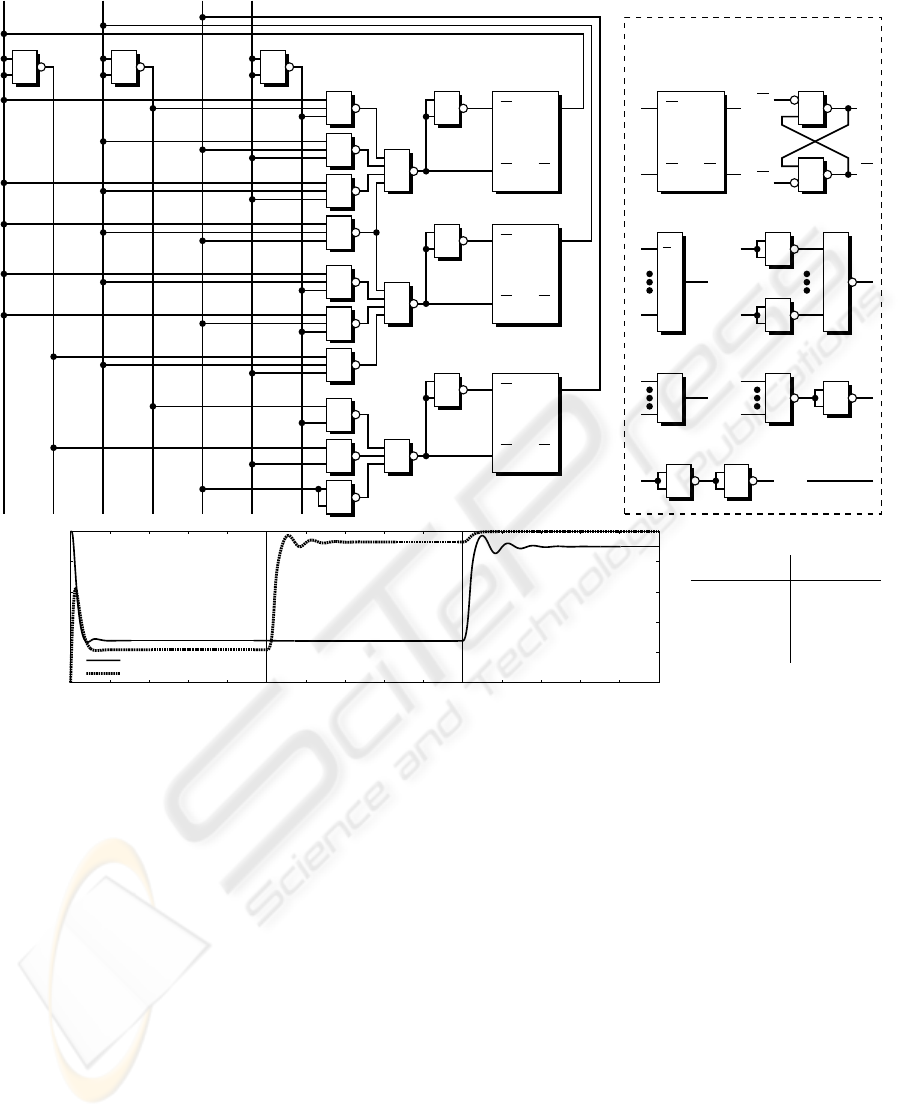
The resulting NAND-based network shown in the
upper part of figure 6 was directly derived from these
transition rules. After backtransformation of this net-
work into the description level of coupled GRNs, we
obtain an artificial biosignalling system consisting of
115 interacting activation resp. repression pathways.
The lower part of figure 6 depicts the normalised con-
centrations of the signalling substances encoding state
bits b
1
and b
3
over the time course for three state tran-
sitions. Effects of signal weakening, also observed in
laboratory studies in vivo (see figure 2), are reflected
by the model based on Hill kinetics.
7 CONCLUSIONS
This paper addresses three strongly interconnected as-
pects of biomolecular computing based on biosignals
processed by GRNs: wetlab implementation of com-
putational units (NAND gate, low active RS flip-flop)
in vivo, homogeneous dynamical modelling of these
units (Hill kinetics), and their composition to comput-
ing agents able to solve real world problems, initially
shown in a conceptual study in silico. We incorpo-
rated AHL as an additional intercellular transcription
factor suitable to switch logic gates. Despite being
rather slow, they convince by their reliability as a re-
quirement for scalability. Flow cytometry provides
a promising method to visualise amounts of output
proteins resulting from computing processes in vivo.
Further studies will consider parallel interactions of
GRNs.
ACKNOWLEDGEMENTS
This work is part of the ESIGNET project (Evolv-
ing Cell Signalling Networks in silico), which has
received research funding from the European Com-
munity’s Sixth Framework Programme (project no.
12789). Further funding from the Federal Ministry of
Education and Research (BMBF, grant 0312704A) is
acknowledged. We are very grateful to J.J. Collins for
providing us with the plasmids and their sequences;
to W. Pompe, G. R¨odel, K. Ostermann, and L. Brusch
BIOSIGNAL-BASED COMPUTING BY AHL INDUCED SYNTHETIC GENE REGULATORY NETWORKS - From an
in vivo Flip-Flop Implementation to Programmable Computing Agents
167

0
0.2
0.4
0.6
0.8
1
0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150
Normalised concentration
Time scale
x=0 x=1 x=1
b1
b3
& & &
&
&
=
&
&
&
>
1
&
=
& &
=
S
R
Q
Q
R
S
Q
Q
&
&
=
&
&
&
&
&
&
&
&
&
&
& &
S
R
Q
Q
S
R
Q
Q
S
R
Q
Q
&
&
&
&
b
1
b
2
b
3
x
b
2
b
3
b
1
b’
2
b’
3
b’
1
x
1 1 0 0 1 00
0 1 0 1 0 1 1
0 1 1 1 1 1 1
final state
reached
simplification
OR gate
low active RS flip−flop
unification to NAND gates
AND gate
Figure 6: Minimal NAND-based logic circuit derived from the finite automaton and dynamical simulation of the system
resulting from coupled GRNs (Copasi ODE solver). Up to 115 regulatory processes interact via signalling molecules (in-
put/output substances of underlying 22 computational units). The diagram depicts the path 110
0
→ 010
1
→ 011
1
→ 111 through
the finite automaton states b
1
b
2
b
3
. While state bit b
2
remains at the high level (not shown), b
1
and b
3
switch twice resp.
once. Hill kinetic parameters were set as follows: m
ij
= 2, Θ
ij
∈ [0.1, 0.3] in accordance with achieving stable system states
corresponding to binary numbers. Normalised concentration levels between 0 and 0.3 are treated as binary 0, values between
0.7 and 1 represent binary 1.
from Dresden University of Technology for their sci-
entific support and V. Helms from Saarland Univer-
sity for administrative support.
REFERENCES
Aoki, T., Kameyama, M., and Higuchi, T. (1992).
Interconnection-free biomolecular computing. IEEE
Computer, 25:41–50.
Baum, E. and Boneh, D. (1999). Running dynamic pro-
gramming algorithms on a DNA computer. DIMACS,
44:77–86. Proceedings Second Meeting on DNA-
Based Computers.
Buchler, N., Gerland, U., and Hwa, T. (2003). On schemes
of combinatorial transcription logic. Proc. Natl. Acad.
Sci. USA, 100(9):5136–5141.
Engebrecht, J. and Silverman, M. (1984). Identification of
genes and gene products necessary for bacterial bio-
luminescence. Proc. Natl. Acad. Sci. USA, 81:4154–
4158.
Gardner, T., Cantor, C., and Collins, J. (2000). Construction
of a genetic toggle switch in escherichia coli. Nature,
403:339–342.
Guido, N., Wang, X., Adalsteinsson, D., McMillen, D.,
Hasty, J., Cantor, C., Elston, T., and Collins, J. (2006).
A bottom-up approach to gene regulation. Nature,
439:856–860.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
168

Hastings, J. and Nealson, K. (1977). Bacterial biolumines-
cence. Annu. Rev. Microbiol., 31:549–595.
Hayat, S., Ostermann, K., Brusch, L., Pompe, W., and
Roedel, G. (2006). Towards in vivo computing: Quan-
titative analysis of an artificial gene regulatory net-
work behaving as a RS flip-flop and simulating the
system in silico. In Proc. Bionetics Cavalese. IEEE.
in print.
Henkel, C., Baeck, T., Kok, J., Rozenberg, G., and Spaink,
H. (2007). DNA computing of solutions to knapsack
problems. Biosystems. in print.
Hinze, T., Hatnik, U., and Sturm, M. (2002). An object
oriented simulation of real occurring molecular bio-
logical processes for DNA computing and its experi-
mental verification. In DNA Computing, volume 2340
of Lecture Notes in Computer Science, pages 1–13.
Huffman, D. (1954). The synthesis of sequential switching
circuits. Journal of the Franklin Institute, 257(3):161–
190.
Kaern, M., Blake, W., and Collins, J. (2003). Engineering of
gene regulatory networks. Annu. Rev. Biomed. Eng.,
5:179–206.
Kobayashi, H., Kaern, M., Araki, M., Chung, K., Gardner,
T., Cantor, C., and Collins, J. (2004). Programmable
cells. Proc. Natl. Acad. Sci. USA, 101:8414–8419.
Magnasco, M. (1997). Chemical kinetics is Turing univer-
sal. Physical Review Letters, 78(6):1190–1193.
Mestl, T., Plahte, E., and Omholt, S. (1995). A mathemati-
cal framework for describing and analysing gene reg-
ulatory networks. J. Theor. Biol., 176:291–300.
Miller, M. and Bassler, B. (2001). Quorum sensing in bac-
teria. Annu. Rev. Microbiol., 55:165–199.
Morris Mano, M. (1991). Digital Design. Prentice-Hall,
second edition.
Ptashne, M. (1992). Genetic Switch: Phage Lambda and
Higher Organisms. Blackwell.
Schaefer, A., Val, D., Hanzelka, B., Cronan jr., J., and
Greenberg, E. (1996). Generation of cell-to-cell sig-
nals in quorum sensing: Acyl homoserine lactone syn-
thase activity of a purified vibrio fischeri LuxI protein.
Proc. Natl. Acad. Sci. USA, 93:9505–9509.
Sprinzak, D. and Elowitz, M. (2005). Reconstruction of
genetic circuits. Nature, 438:443–448.
Thomas, R. (1991). Regulatory networks seen as asyn-
chronous automata: a logical description. J. Theor.
Biol., 53:1–23.
Weiss, R., Homsy, G., and Knight jr., T. (1999). Toward
in-vivo digital circuits. DIMACS. Workshop on Evo-
lution as Computation.
Yokobayashi, Y., Weiss, R., and Arnold, F. (2004). Directed
evolution of a genetic circuit. Proc. Natl. Acad. Sci.
USA, 99:16587–16591.
BIOSIGNAL-BASED COMPUTING BY AHL INDUCED SYNTHETIC GENE REGULATORY NETWORKS - From an
in vivo Flip-Flop Implementation to Programmable Computing Agents
169