TRADITIONAL AVERAGING, WEIGHTED AVERAGING, AND

ERPSUB FOR ERP DENOISING IN EEG DATA

A Comparison of the Convergence Properties

Andriy Ivannikov, Tommi K¨arkk¨ainen, Tapani Ristaniemi

Department of Mathematical Information Technology, University of Jyv¨askyl¨a

P.O. Box 35 (Agora), FIN-40014, Jyv

askyl

a, Finland

Heikki Lyytinen

Department of Psychology, University of Jyv¨askyl¨a

P.O. Box 35 (Agora), FIN-40014, Jyv

askyl

a, Finland

Keywords:

Convergence, EEG, ERP, Denoising, Weighted Averaging, SNR, Source Separation.

Abstract:

In this article we compare the convergence rates at increase of the number of processed trials of the three meth-

ods applied nowadays in electroencephalography research to denoising of event-related potentials: traditional

averaging, weighted averaging, and ERPSUB. We derive the weighted averaging procedure by maximizing

signal-to-noise ratio in the averaged subject responses and show, thereby, that maximizing signal-to-noise ra-

tio criterion is equivalent to minimizing the originally proposed mean-square error criterion in the sense of the

weighted averaging problem solving. Moreover, in order to characterize fully the performance of the selected

methods, we compare also noise reduction rates in estimates of event-related potentials provided by methods,

while the number of processed trials increases.

1 INTRODUCTION

Reliable characterization of event-related potentials

(ERPs) is a central task in electroencephalography

(EEG) data processing. ERP is a concept used in

EEG research to denote brain electromagnetic poten-

tials occurring as responses to the external or men-

tal events, whose quantitativeunderstanding underlies

many neuropsychological studies and clinical diagno-

sis (Huttunen et al., 2007; Luu et al., 2004; Makeig

et al., 1999; N¨a¨at¨anen, 1992). However, the signal-

to-noise ratio (SNR) is very low in a single mea-

surement (trial) of the brain response following the

stimulation event, which makes it impossible to iden-

tify ERP characteristics, such as amplitude and la-

tency, reliably. In order to increase SNR and, hence,

estimate reliably ERP characteristics, many trials of

equal length and synchronized to the same event are

measured from different locations on the scalp (chan-

nels) and averaged channel-wise (see Sect. 2). Aver-

ages of many trials for every channel are assumed to

have high SNR and important ERP characteristics can

be identiﬁed then from the averages with the accuracy

depending on the number of trials used for averaging.

Moreover, besides improving the reliability of the

estimates of ERP characteristics, it is also important

to shorten the experiment time, because subjects un-

der consideration suffer from the long time lasting ex-

periments. They get tired, lose attention and can not

adequately perform the experimental tasks anymore.

As a consequence, data become less informative from

the experimental design point of view. Furthermore,

for some groups of probationers (infants or patients)

long experiments may be too demanding.

Basically, we need less trials to shorten the time

of the experiment. Hence, our attention is focused on

methods, which extract useful information from EEG

data more effectively than the conventional averag-

ing does. This allows obtaining the desired accuracy

of ERP characteristics using fewer trials and, hence,

shorter experiment. We consider two methods that

were developed to increase SNR in the subject aver-

ages as compared to the conventional averaging pro-

cedure: weighted averaging (Hoke et al., 1984) and

ERPSUB (Ivannikov et al., 2007).

An important assumption underlying the averag-

ing in electroencephalography research is the ergod-

icity of the noise. However,we should be realistic and

195

Ivannikov A., Kärkkäinen T., Ristaniemi T. and Lyytinen H. (2008).

TRADITIONAL AVERAGING, WEIGHTED AVERAGING, AND ERPSUB FOR ERP DENOISING IN EEG DATA - A Comparison of the Convergence

Properties.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 195-202

DOI: 10.5220/0001056901950202

 SciTePress

understand that this assumption is violated to some

extent in practical applications. This leads us to a

situation, when the variance of the noise is different

across trials. It then turns out that SNR in the aver-

aged responses can be boosted by weighting the tri-

als inversely to the variance of the noise they contain.

The formal derivation of this result was originally ob-

tained in (Hoke et al., 1984) by minimizing the mean-

square error criterion. In (Davila and Mobin, 1992) a

similar technique has also been derived by maximiz-

ing SNR in the average using Rayleigh quotient and

solving the generalized eigenvalue problem. Later,

in (Łe¸ski, 2002) robust version of weighted averag-

ing was proposed and further developed into com-

putationally more effective algorithm in (Łe¸ski and

Gacek, 2004). In this paper we obtain essentially

same result as in (Hoke et al., 1984) by maximiz-

ing SNR criterion, but using different derivation pro-

cedure than that used in (Davila and Mobin, 1992)

and show, thereby, that SNR criterion is equivalent

to the mean-square error criterion in the sense of the

weighted averaging problem solving.

ERPSUB method utilizes the problem speciﬁc as-

sumptions for ERP/noise linear subspaces separation

in multichannel EEG data and results in more effec-

tive denoising of ERPs comparing to the conventional

averaging (Ivannikov et al., 2007). Method automat-

ically solves the component classiﬁcation problem

for a priori known dimensionality of ERP subspace.

Moreover, it contains also means for estimating the

dimensionality of ERP subspace, if prior knowledge

is absent, with the accuracy depending on the close-

ness of the data properties to the values provided by

the ideal assumptions.

Since we are interested in decreasing the experi-

mental time (minimizing number of trials necessary

for reliable ERP identiﬁcation), in this paper we con-

centrate on and compare the convergencerates of ERP

estimates provided by selected methods (traditional

averaging approach, weighted averaging, and ERP-

SUB), while the number of processed trials increases.

Moreover, in order to give a comprehensive evalua-

tion of the methods’ performance, we also compare

the noise reduction rates in ERP estimates for the

same conditions.

The structure of the work is as follows. First, in

Sect. 2, we describe the experimental data and formu-

late the research area. Then, in Sect. 3, the methods

are discussed. Section 4 represents the experimental

results. In Sect. 5, conclusions are drawn.

2 PRELIMINARIES

In this article we used EEG data that were introduced

and studied in (Huttunen et al., 2007) and (Kalyakin

et al., 2007). The same data were utilized also for the

purposes of testing in (Ivannikov et al., 2007). The

data collection experimental design was targeted to

elicit mismatch negativity (MMN) component of au-

ditory ERP. In fact, MMN has turned out to be espe-

cially useful for the investigation of the brain basis of

human auditory cognition (N¨a¨at¨anen, 1992).

In the data collection experiments, the experimen-

tal paradigm proposed in (Pihko et al., 1995) was

used. It is based on a sequence of standard stim-

uli consisting of continuously (uninterruptedly) alter-

nated sounds of 600 Hz and 800 Hz, each lasting 100

ms. Two types of deviant stimuli are randomly pre-

sented in this sequence with the frequency of 600 Hz

and duration of 30 ms or 50 ms. The measured trials

contain 300 ms of recordings before the start of the

deviant tone and 350 ms after the start of the deviant

tone. Measurements were collected with the sam-

pling rate 200 Hz, thus, giving 130 time points for

each trial. There were 102 participants (or subjects)

involved in the data collection experiment. Measure-

ments were recorded using 12-electrodes scheme re-

sulting in 350 trials collected for each of 102 subjects,

each of the two deviants and each of the nine chan-

nels of EEG data (i.e., C3, C4, Cz, F3, F4, Fz, Pz,

M1, M2) and the two channels of electrooculography

(EOG) data (i.e., ER, EL). An additional nose elec-

trode was used as a reference point.

We assume that each recorded trial x

(t) contains

both the weighted sum of the time-locked brain re-

sponses s

(t) assumed to be deterministic through all

trials and the weighted sum of the noise sources n

(t),

such as spontaneous EEG and artifacts (Vig´ario,

1997; Jung et al., 2000). Noises n

(t) are assumed to

be uncorrelated with each other and with s

(t). Then,

without loss of generality we can assume that x

(t),

(t), and n

(t) are zero mean variables, since data

always can be centered. Hence, the simplest additive

model to describe the phenomenon reads as

(t) = s

(t) + n

(t), (1)

where i = 1,...,N, t = 1,...,T, and k = 1, ..., K. Here

N denotes the number of measured trials, T is the

number of time points per trial, and K denotes the

number of measured channels. The conventional av-

eraging operation is performed for each channel sep-

arately and is described by formula:

(t) =

∑

i=1

(t) = s

(t) + n

(t), (2)

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

196

where s

(t) is the time-locked ERP constituent (sig-

nal of interest) and n

(t) is the noise constituent in

the average. The resulting average in (2) is assumed to

have higher SNR than the single trial does that is con-

ﬁrmed by practical experience and theoretical compu-

tations (N¨a¨at¨anen, 1992; Furst and Blau, 1991).

3 METHOD DESCRIPTION

3.1 Weighted Averaging

The variance of the sum of N stochastic variables can

be expressed through the formula

∑

i=1

(t)

∑

i=1

(t)) + 2

∑

i< j

Cov

, (3)

where Cov

= E[x

(t)x

(t)] denotes the covariance

between the two zero mean stochastic variables or tri-

als x

(t) and x

(t), and σ denotes the standard devia-

tion. To simplify the following discussion we omit the

channel index k throughout the paper assuming that

all channels are treated in the similar way. Therefore,

for the weighted sum/average of trials

∑

i=1

(t)

and taking into account that the covariance of the

two perfectly linearly correlated signals equals to the

product of their standard deviations, we have

∑

i=1

(t)

∑

i=1

∑

i=1

+ 2σ

N−1

∑

i=1

∑

j=i+1

, (4)

where σ

denotes the variance of the signal and σ

the variance of the noise in i-th trial. Then the portions

of the total variance σ

and σ

that are contributed

by the time-locked signals and noise sources, corre-

spondingly, to the weighted sum (normal average in

case a

, ∀i = 1,. ..,N) of N trials read as

= σ

∑

i=1

, (5)

∑

i=1

. (6)

We deﬁne SNR in the weighted sum of N trials as

the variance of ERP constituent in this sum divided

by the variance of the noise constituent:

SNR

(7)

and try to maximize its value in order to determine

the optimal values of a

’s. For this purpose, taking the

partial derivatives of σ

and σ

with respect to a

, we

have

∂ σ

∂a

= 2σ

∑

j=1

, ∀1 ≤ i ≤ N, (8)

∂σ

∂a

= 2a

, ∀1 ≤ i ≤ N. (9)

Therefore, the partial derivative of SNR with respect

to a

is given by

∂SNR

∂a

∂σ

∂a

− σ

∂σ

∂a





, ∀1 ≤ i ≤ N. (10)

Saddle points in the a

’s coordinate space can be

found by equating the numerator of equation (10) to

zero assuming σ

6= 0. Therefore, the problem can be

expressed through a system of equations



∑

j=1



− σ

) = 0,

∀1 ≤ i ≤ N. (11)

Subtracting any two equations in this system, we ob-

tain

= a

, ∀1 ≤ i, j ≤ N. (12)

Plugging a

back to the system of equations

(11), we get a system of identical equations after some

manipulations. Moreover, since the values of weight-

ing coefﬁcients a

’s were not ﬁxed in this operation,

they can be arbitrary within the constraint (12). This

means, in turn, that

= a

= C, ∀1 ≤ i, j ≤ N, (13)

where C can be any constant. Hence, the solution has

a form

, ∀1 ≤ i ≤ N. (14)

It is easy to check that this extremum point is the max-

imum by substituting a

±∆, ∀1 ≤ i ≤ N in (11),

where ∆ > 0 is an inﬁnitely small shift.

Assuming SNR in a single trial is very low (this

follows from the magnitude level of the time-locked

signal ≈ 3–5µV compared to the magnitude level of

the trial itself ≈ 50–100µV), we can disregard the

variance contributed by the time-locked signal to the

trial and approximate

≈ σ

. (15)

Thus, we can approximately compute the coefﬁcients

’s by arbitrarily ﬁxing C constant ﬁrst.

TRADITIONAL AVERAGING, WEIGHTED AVERAGING, AND ERPSUB FOR ERP DENOISING IN EEG DATA - A

Comparison of the Convergence Properties

197

Note that in (Hoke et al., 1984) the minimization

of the mean-square error leads to a single unique so-

lution, whereas in our case the maximization of SNR

yields an inﬁnite set of solutions due to the arbitrary

choice of C in (14). This result can be explained by

the obvious reasoning that only the ratio between a

’s

is emphasized by SNR criterion (the weighted sum

can be multiplied by any number keeping SNR on

a same level), whereas the solution based on mini-

mizing mean-square error criterion is associated with

the original level of ERP signal and with the highest

SNR as well. Hence, in order to correct the level of

ERP signal to original in the weighted average with

weighting coefﬁcients ﬁxed as in (14), where C is ar-

bitrary, we need to multiply

∑

i=1

(t) by a correc-

tion factor α that eliminates uncertainty introduced by

arbitrariness of C. Apparently α depends on C and

plays role of a constraint imposed on C and a

’s that

speciﬁes only single set of a

’s preserving the original

level of ERP signal in the weighted average. From (5)

α is obviously expressed through the formula

α =

/σ

∑

i=1

. (16)

After embedding the correction factor α into (14)

the ﬁnal solution for the weighting coefﬁcients be-

comes

= σ

−2

∑

j=1

−2

, ∀1 ≤ i ≤ N (17)

that coincides with the results from (Hoke et al.,

1984). These values of the weighting coefﬁcients are

unique in the sense that they are connected to the orig-

inal level of ERP signal and, thus, do not require mul-

tiplication by the correction factor α, which equals to

1 in this case.

3.2 ERPSUB

In the contemporary research EEG data is often con-

sidered in the scope of the linear instantaneous noise-

less mixing model, which is also assumed in this pa-

per:

= A·Y

, ∀i = 1,. .., N, (18)

where X

is a matrix of size K × T, which contains

measurements from K channels and one trial of length

T time points, Y

is a matrix of size K × T, which con-

tains the realizations of K sources of length T time

points, and A stands for the mixing matrix. It is as-

sumed that every row in X

has zero mean for all i, i.e.

the data are centered. In addition we assume that the

mixing matrix A does not change in time. Practically

it means that for one subject during one experiment

with the static conditions matrix A stays the same for

all trials within the experiment. Therefore, we are al-

lowed to form a data matrix by concatenating matrices

channel-wise:

X = A·Y, (19)

where X = [X

... X

] is the matrix of con-

catenated measurements of size K × TN and Y =

... Y

] is the matrix of concatenated realiza-

tions of the sources of the same size. Matrix equiva-

lent of (2) can now be written as

X =

∑

i=1

= A

∑

i=1

= AY. (20)

Furthermore, in the framework of the model (18)

it is assumed that all K measurements in every multi-

dimensional trial X

are linearly independent and the

number of sources does not exceed the number of

channels. These assumptions are introduced to ensure

that measurements form the basis for the linear space

of the same dimension as sources do. This, in turn,

guarantees the existence of the pure signal and noise

subspaces in theory. Both assumptions are practically

addressed by reasonable selection of K and T param-

eters. Moreover, we assume that subspaces of ERP

signals and noise are statistically independent. The

imposed assumptions, except the one concerning the

linear independenceof measurements, are rather strict

and can not be completely justiﬁed in practical ap-

plications. However, they are necessary on the stage

of the method development. In real situations one is

instructed to reinterpret the results of the method ac-

cording to the types and extent of the assumptions’

violations.

The main idea of ERPSUB is to use the relevant

information stored in data along all time, trial, and

channel dimensions, while separating ERP/noise sub-

spaces. In contrary, most of the Independent Com-

ponent Analysis (ICA) methods also applied in EEG

data processing to ERP/noise sources separation ex-

ploit the information kept along the time and chan-

nel dimensions only, whereas the trial dimension is

ignored (Hyv¨arinen et al., 2001; Jung et al., 2000;

Vig´ario, 1997). Traditional averaging is one-channel

technique, and it exploits the information hidden in

trial dimension only for ERP denoising. Weighted av-

eraging is also one-channel procedure, but it utilizes

the information taken from trial and time dimensions

for the purposes of ERP denoising. ERPSUB exploits

the fact that after the averaging the variance of data

should decrease along the directions in the noise sub-

space, while the variance along the signal directions

should stay on the original level in ideal conditions.

This means that after whitening, which should make

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

198

50 100 150 200 250 300 350

10e−4

10e−3

10e−2

10e−1

10e0

10e1

10e2

10e3

MSD

, µV

50 100 150 200 250 300 350

10e−4

10e−3

10e−2

10e−1

10e0

10e1

10e2

10e3

50 100 150 200 250 300 350

10e−4

10e−3

10e−2

10e−1

10e0

10e1

10e2

10e3

50 100 150 200 250 300 350

10e−4

10e−3

10e−2

10e−1

10e0

10e1

10e2

10e3

MSD

, µV

50 100 150 200 250 300 350

10e−4

10e−3

10e−2

10e−1

10e0

10e1

10e2

10e3

50 100 150 200 250 300 350

10e−4

10e−3

10e−2

10e−1

10e0

10e1

10e2

10e3

50 100 150 200 250 300 350

10e−4

10e−3

10e−2

10e−1

10e0

10e1

10e2

10e3

N, number of trials

MSD

, µV

50 100 150 200 250 300 350

10e−4

10e−3

10e−2

10e−1

10e0

10e1

10e2

10e3

N, number of trials

50 100 150 200 250 300 350

10e−4

10e−3

10e−2

10e−1

10e0

10e1

10e2

10e3

N, number of trials

Conventional Average

Weighted Average

ERPSUB

Figure 1: The averaged over 102 subjects MSD tracks provided by traditional averaging, weighted averaging and ERPSUB

(nine EEG channels, 30ms deviant, logarithmic scale).

subspaces orthogonal and standardize the data to sim-

ilar variances along all directions, and averaging ERP

components should have the largest variances in con-

trary to the noise components, and, hence, subspaces

can be extracted by standard linear Principal Com-

ponent Analysis (PCA) algorithm (Hyv¨arinen et al.,

2001; Oja, 1992). In practice, however, the variance

of data most likely will reduce along all directions af-

ter the averaging, because subspaces are overlapped,

and additive noise is always present, and, thus, pure

signal/noise subspaces do not exist. In this case the

results are interpreted in terms of SNR: higher SNR

is obtained in data projected to the directions describ-

ing larger data variations after whitening and aver-

aging. Thus, practically, we intend to separate the

subspace of dimension N

ERP

having maximal possi-

ble SNR from the subspace of dimension K − N

ERP

with the minimal possible SNR. As one can see, ERP-

SUB is based on a sequence of linear transformations

applied in a problem-speciﬁc manner to multidimen-

sional EEG data and results in effective denoising of

ERP signals (Ivannikov et al., 2007).

ERPSUB:

1. Whiten the centered concatenated data:

Z = D

−1/2

X, (21)

where matrices D andW are taken from the eigen-

value decomposition

Σ = WDW

of the estimated

covariance matrix

Σ = XX

/(TN − 1).

2. Average the whitened data:

Z = D

−1/2

X. (22)

3. Apply the standard linear PCA to the averaged

whitened data

′

ERP

= ∆

ERP

−1/2

X, (23)

where matrix W

is obtained from the eigenvalue

decomposition ZZ

/(T − 1) = WDW

and ∆

ERP

is the diagonal projection matrix having ones on

ERP

ﬁrst diagonal elements corresponding to the

components contributing energy to ERP (maximal

SNR) subspace and zeros otherwise. Here, N

ERP

is the amount of assumed ERP sources present in

EEG measurements. In practice, when pure sig-

nal/noise subspaces do not exist, N

ERP

has differ-

ent meaning interpreted in terms of SNR. In this

TRADITIONAL AVERAGING, WEIGHTED AVERAGING, AND ERPSUB FOR ERP DENOISING IN EEG DATA - A

Comparison of the Convergence Properties

199

50 100 150 200 250 300 350

10e−1

10e0

10e1

10e2

10e3

, µV

50 100 150 200 250 300 350

10e−1

10e0

10e1

10e2

10e3

50 100 150 200 250 300 350

10e−1

10e0

10e1

10e2

10e3

50 100 150 200 250 300 350

10e−1

10e0

10e1

10e2

10e3

50 100 150 200 250 300 350

10e−1

10e0

10e1

10e2

10e3

50 100 150 200 250 300 350

10e−1

10e0

10e1

10e2

10e3

50 100 150 200 250 300 350

10e−1

10e0

10e1

10e2

10e3

N, number of trials

50 100 150 200 250 300 350

10e−1

10e0

10e1

10e2

10e3

N, number of trials

50 100 150 200 250 300 350

10e−1

10e0

10e1

10e2

10e3

N, number of trials

Conventional Average

Weighted Average

ERPSUB

−

, µV

−

, µV

−

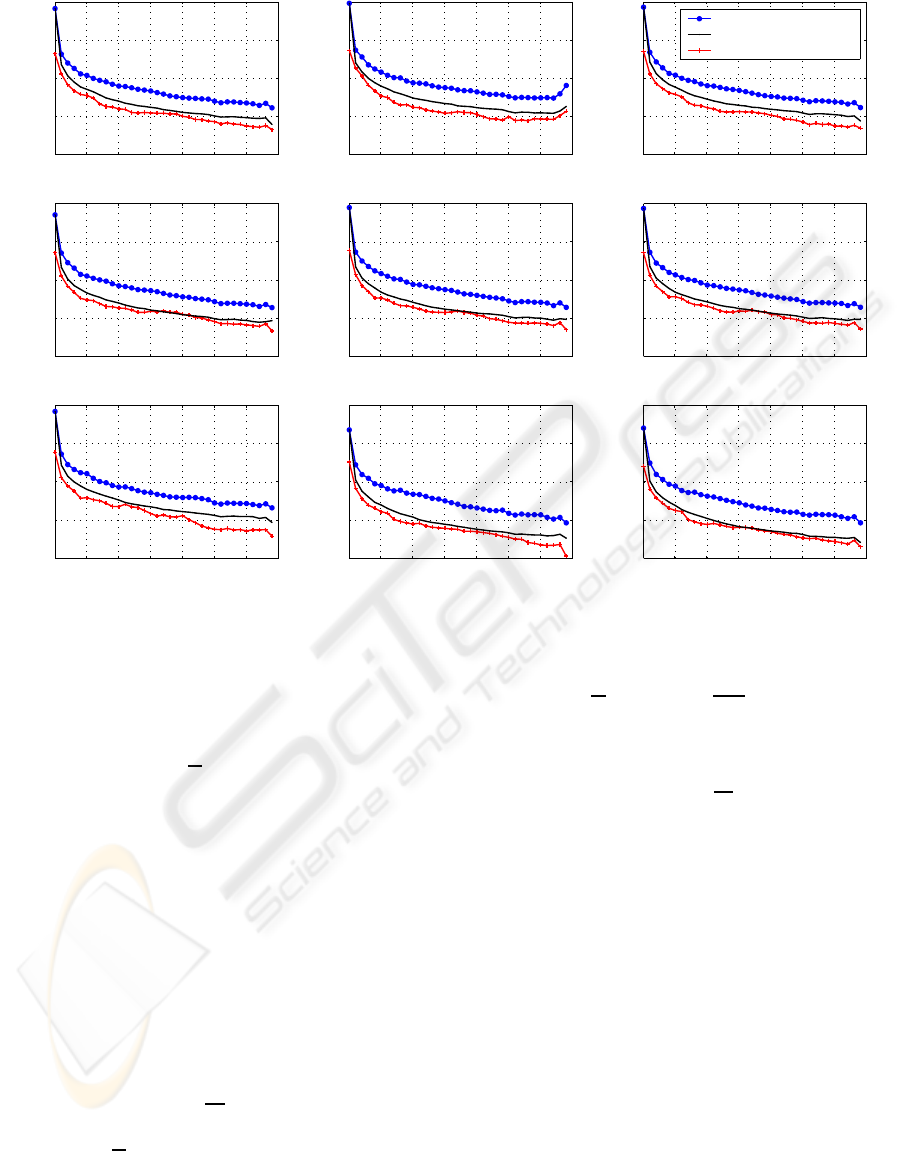
Figure 2: The averaged over 102 subjects tracks of the remaining noise variance in ERP estimates provided by traditional

averaging, weighted averaging and ERPSUB (nine EEG channels, 30ms deviant, logarithmic scale).

case N

ERP

is the amount of the components hav-

ing largest SNR, which in our opinion describe

ERP and noise variations in channels in propor-

tions providing suitable SNR and tolerable ERP

energy loss. Hence, Y

′

ERP

is a matrix of the av-

eraged components, where all components from

noise (minimal SNR) subspace are zeroed. Note

that ERP components have the largest correspond-

ing eigenvalues and, thus, the component classi-

ﬁcation problem is solved automatically for ﬁxed

ERP

. In addition, if the difference between eigen-

values corresponding to ERP and noise compo-

nents is clearly observed, one can estimate N

ERP

value providing optimal separation of the compo-

nents into subspaces in the sense of SNR and ERP

energy loss. Moreover, each K-dimensional trial

can be decomposed into the components using

the same transformation as in (23):

′

ERPi

= ∆

ERP

−1/2

, (24)

4. The matrix Y

′

ERP

containing only averaged com-

ponents related to ERP subspace is then trans-

formed back to the original data space (channels)

to result in the subject average with the reduced

noise:

ERP

= WD

1/2

′

ERP

. (25)

A similar relation applies also to a single trial de-

noising:

ERPi

= WD

1/2

′

ERPi

. (26)

4 EXPERIMENTAL RESULTS

It was noticed during the simulations and is theoreti-

cally predictable that the weighted averaging method

is highly sensitive to the trials having small portions

of variance concentrated on short time intervals. Gen-

erally, such trials do not carry much of the informa-

tion and are usually recorded at the saturation state of

the ampliﬁer, when parts of the trials are truncated re-

sulting in peaks alternating with ﬂat periods. Satura-

tion state occurs, when signal exceeds the dynamical

range of the ampliﬁer. The weighting coefﬁcients a

’s

assigned for such trials are very large following the al-

gorithm. As a consequence, when trials are weighted,

peaks in truncated trials become very strong against

a background of other trials’ amplitude resulting in a

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

200

high frequency noise in the averaged signal. To an-

nul the harmful consequences introduced by the trun-

cated trials we performed the trial rejection procedure

for our data before doing the computations. The suc-

cessful upper limit of the trial’s variance for the trial

removal was 30µV

, which ﬁnally rejected all trun-

cated trials in our database.

Apparently, for our problem the converged ERP

estimate (subject average) is indicated by only in-

signiﬁcant change introduced by the consequent trial.

We measure the amount of change between the two

subsequent ERP estimates in one channel for method

LABEL by MSD score:

MSD

LABEL

∑

t=1

LABEL

(t) − x

LABEL

N−1

(t))

where x

LABEL

(t) denotes ERP estimate obtained after

application of a particular method LABEL involving

N trials. Thus, for example, for ERPSUB x

ERPSUB

(t)

equals to a rowin the matrix of averaged ﬁltered chan-

nels X

ERP

corresponding to the considered channel;

for weighted averaging x

(t) =

∑

i=1

(t), where

’s are computed as in (17) substituting approxima-

tion from (15) for σ

for all i = 1,... ,N. To compare

the convergence rates of ERP estimates provided by

methods under consideration at increase of the num-

ber of processed trials, we computed averaged over

102 subjects MSD values for N = 1,... ,350 (MSD

tracks) for each method (see Fig. 1). We did this

for the nine EEG channels and for 30ms deviant only,

where ERP appeared to be the strongest. The value

of N

ERP

parameter of ERPSUB method was set to 3,

that is, a good choice of maximal SNR subspace di-

mension for our data, because signal loss is insignif-

icant and noise reduction is sufﬁciently high result-

ing in essential SNR increase (Ivannikov et al., 2007).

According to the obtained results, the weighted av-

eraging procedure outperforms both the traditional

averaging scheme and ERPSUB algorithm, because

MSD provided by weighted averaging, in general, de-

creases faster than for other methods at increase of

the number of processed trials. The superiority of the

weighted averaging here is probably a consequence of

the core idea underlying the method. Weighted aver-

aging is designed in a way that trials are ’equalized’

in the sense of the variance. This should make the

convergence of the ERP estimate smoother and faster.

Although application of ERPSUB should result in

higher noise reduction rate than the conventional av-

erage provides (Ivannikov et al., 2007), ERPSUB

has shown the lowest convergence rate of MSD to

zero. Most likely this happens, because new-coming

trial inﬂuences the denoising of all previous trials by

changing the projection axes. Since the shapes of all

ﬁltered trials are affected, when new trial is added to

processing, the difference between the two adjacent

ERP estimates becomes more signiﬁcant.

Therefore, in order to have a complete and fair

comparative picture of the methods’ performance, we

also computed averaged over 102 subjects remaining

noise variances in ERP estimates obtained under the

same conditions as used in the ﬁrst test (see Fig. 2).

We used the following estimate of the noise variance

in the averaged brain responses taken from (van de

Velde, 2000):

2 LABEL

= var{

∑

i=1

(−1)

LABEL

(t)}, (27)

where x

LABEL

(t) is the modiﬁed trial x

(t) obtained

after application of method LABEL, and

2 LABEL

the estimate of the remaining noise variance in ERP

estimate obtained after application of method LABEL

involving N trials. For instance, x

(t) = ba

(t),

where ba

is computed as in (17) replacing σ

with

the approximation from (15) for all i = 1,. ..,N; and

ERPSUB

(t) equals to a row in the matrix of ﬁltered

trial X

ERPi

corresponding to the considered channel.

In this test the performance order of the methods ap-

peared to be different. ERPSUB has shown now the

highest effectiveness in the sense of the noise reduc-

tion rate, since the remaining noise variance in ERP

estimate provided by ERPSUB, in general, decreased

faster than for other methods at increase of the num-

ber of processed trials. This outstanding performance

can be explained here by the algorithmic nature of

ERPSUB, which simultaneously operates through all

time, trial, and channel dimensions that allows more

efﬁcient extraction of the information discriminating

ERP and noise from data. The conventional averag-

ing has shown the lowest noise reduction rate in ERP

estimate following the results of the test.

5 CONCLUSIONS

In this article we compared the performance of the

three methods used nowadays in EEG research for

ERP denoising: conventional averaging, weighted av-

eraging and ERPSUB. For this purpose we carried out

two tests investigating the convergence and the noise

reduction rates in ERP estimates provided by the se-

lected methods at increase of the number of processed

trials. The convergencerate of ERP estimate appeared

to be the highest for the weighted averaging technique

and the lowest for ERPSUB. However, ERPSUB has

shown stronger noise reduction power than the tra-

ditional and weighted averaging methods have. The

noise reduction rate in ERP estimate provided by the

TRADITIONAL AVERAGING, WEIGHTED AVERAGING, AND ERPSUB FOR ERP DENOISING IN EEG DATA - A

Comparison of the Convergence Properties

201

traditional averaging was the poorest among tested

methods.

The paper touches practical issues the neuropsy-

chology researchers are faced with during EEG/ERP

data processing and analyzing. Namely, it points out

the bottlenecks of the traditional averaging technique

used for the time-locked brain responses denoising.

The roots of these bottlenecks are connected to the

violation of the assumptions underlying the averag-

ing in real applications and insufﬁciently powerful

’decoding’ of the relevant information ’encrypted’ in

the data. The weighted averaging method addresses

the bottlenecks, which arise due to the violation of

the assumptions underlying traditional averaging. We

have shown that this strategy for improving the per-

formance and the reliability of the traditional averag-

ing technique can be derived based on different crite-

ria and, in particular, SNR and mean-square error as it

has been shown in (Hoke et al., 1984). ERPSUB tries

to eliminate the second type of the bottlenecks, which

come from the disability of the traditional averaging

to effectively extract from data the overall available

information related to ERP and noise discrimination.

ERPSUB ’decrypts’ more effectively this information

hidden in data, since it operates through all time, trial,

and channel dimensions.

REFERENCES

Davila, C. E. and Mobin, M. S. (1992). Weighted averaging

of evoked potentials. IEEE Transactions on Biomedi-

cal Engineering, 39(4):338–345.

Furst, M. and Blau, A. (1991). Optimal a posteriori time

domain ﬁlter for average evoked potentials. IEEE

Transactions on Biomedical Engineering, 38(9):827–

833.

Hoke, M., Ross, B., Wickesberg, R., and L¨utkenh¨oner, B.

(1984). Weighted averaging - theory and application

to electric response audiometry. Electroenceph. Clin.

Neurophysiol., 57:484–489.

Huttunen, T., Halonen, A., Kaartinen, J., and Lyytinen, H.

(2007). Does mismatch negativity show differences

in reading disabled children as compared to normal

children and children with attention deﬁcit? Develop-

mental Neuropsychology, 31(3):453–470.

Hyv¨arinen, A., Karhunen, J., and Oja, E. (2001). Indepen-

dent component analysis. John Wiley & Sons, Inc.

Ivannikov, A., K¨arkk¨ainen, T., Ristaniemi, T., and Lyytinen,

H. (2007). Extraction of ERP from EEG data. In 9th

International Symposium on Signal Processing and its

Applications.

Jung, T.-P., Makeig, S., Humphries, C., Lee, T. W., McK-

eown, M. J., Iragui, V., and Sejnowski, T. (2000).

Removing electroencephalographic artifacts by blind

source separation. Psychophysiology, 37:163–178.

Kalyakin, I., Gonz´alez, N., Joutsensalo, J., Huttunen, T.,

Kaartinen, J., and Lyytinen, H. (2007). Optimal dig-

ital ﬁltering versus difference waves on the mismatch

negativity in an uninterrupted sound paradigm. Devel-

opmental Neuropsychology, 31(3):429–452.

Łe¸ski, J. (2002). Robust weighted averaging. IEEE Trans-

actions on Biomedical Engineering, 49(8):796–804.

Łe¸ski, J. and Gacek, A. (2004). Computationally effective

algorithm for robust weighted averaging. IEEE Trans-

actions on Biomedical Engineering, 51(7):1280–

1284.

Luu, P., Tucker, D., and Makeig, S. (2004). Frontal mid-

line theta and the error-related negativity: neurophys-

iological mechanisms of action regulation. Clinical

Neurophysiology, 115(8):1821–35.

Makeig, S., Westerﬁeld, M., Townsend, J., Jung, T.-P.,

Courchesne, E., and Sejnowski, T. (1999). Func-

tionally independent components of the early event-

related potentials in a visual spatial attention task.

Philosophical Transactions of the Royal Society B: Bi-

ological Sciences, 354:1135–44.

N¨a¨at¨anen, R. (1992). Attention and brain function.

Lawrence Erlbaum Associates, Hillsdale, New Jersey.

Oja, E. (1992). Principal components, minor components,

and linear neural networks. Neural Networks, 5:927–

935.

Pihko, E., Lepp¨asaari, T., and Lyytinen, H. (1995). Brain

reacts to occasional changes in duration of elements

in continues sound. NeuroReport, 6:1215–18.

van de Velde, M. (2000). Signal validation in electroen-

cephalography research. PhD thesis, Eindhoven Uni-

versity of Technology.

Vig´ario, R. (1997). Extraction of ocular artifacts from

EEG using independent component analysis. Elec-

troencephalography and Clinical Neurophysiology,

103:395–404.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

202