A VOCAL TRACT VISUALISATION TOOL FOR A

COMPUTER-BASED SPEECH TRAINING AID FOR

HEARING-IMPAIRED INDIVIDUALS

Abdulhussain E. Mahdi

Department of Electronic & Computer Engineering, University of Limerick, Limerick, Ireland

Keywords: Speech Production, Vocal Tract Models, Articulatory Training, Linear Prediction Coding.

Abstract: This paper describes a computer-based software prototype tool for visualisation of the vocal-tract, during

speech articulation, by means of a mid-sagittal view of the human head. The vocal tract graphics are

generated by estimating both the area functions and the formant frequencies from the acoustic speech signal.

First, it is assumed that the speech production process is an autoregressive model. Using a linear prediction

analysis, the vocal tract area functions and the first three formants are estimated. The estimated area

functions are then mapped to corresponding mid-sagittal distances and displayed as 2D vocal tract lateral

graphics. The mapping process is based on a simple numerical algorithm and an accurate reference grid

derived from x-rays for the pronunciation of a number English vowels uttered by different speakers. To

compensate for possible errors in the estimated area functions due to variation in vocal tract length between

speakers, the first two sectional distances are determined by the three formants. Experimental results show

high correlation with x-ray data and the PARAFAC analysis. The tool also displays other speech parameters

that are closely related to the production of intelligible speech and hence would be useful as a visual

feedback aid for speech training of hearing–impaired individuals.

1 INTRODUCTION

The process of learning to speak in the case of

people with normal hearing is primarily aided by

auditory feedback. However, for those who suffer

from deafness, learning to speak naturally is a very

difficult process. With limited auditory capability, a

hearing-impaired person often lacks models of

speech targets necessary to produce normal speech.

In an effort to overcome this difficulty, many

attempts have been made to provide a substitute for

the feedback mechanism with visual speech display

devices (Choi, 1982; Bunnell et. Al., 2000; Mashie.

1995). However, without any articulatory correlate,

the benefits of such devices were limited. In order to

produce a natural and intelligible speech, a speaker

needs to know how to use the vocal organs in

regards to correct position of the articulators,

breathing, loudness, rhythm and nasalization

(Eriksson, et. al., 2005) . Hence the availability of

visual information regarding these aspects would

greatly help the hearing-impaired improving their

speaking abilities.

This paper describes a system which visualises a

speaker’s vocal tract by means of mid-sagittal

graphical plots of the human head. The vocal tract

shapes, and other related speech parameters, are

graphically displayed on a PC-monitor using

information extracted directly from the acoustic

speech signal as picked up by a microphone or

loaded from an audio file. To estimate the necessary

parameters, it is assumed that the speech production

process is an autoregressive (AR) model. The vocal

tract area functions, log spectra and the first three

formants are then estimated, by employing a linear

prediction (LP) analysis, and used to construct the

corresponding vocal tract graphics and other

parameters display.

2 SPEECH ANALYSIS MODEL

Speech is the acoustic wave that is radiated from the

vocal system when air is expelled from the lungs and

the resulting flow of air is perturbed by a

constriction somewhere in the vocal tract. This

speech production process can be practically

modelled using the well-known all-pole source-filter

approach, which represents the speech signal in

terms of an AR model (Quatieri, 2002). According

153

E. Mahdi A. (2008).

A VOCAL TRACT VISUALISATION TOOL FOR A COMPUTER-BASED SPEECH TRAINING AID FOR HEARING-IMPAIRED INDIVIDUALS.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 153-158

DOI: 10.5220/0001057201530158

 SciTePress

to this model, speech is split into a rapidly varying

excitation signal, generated by an impulse train input

or a random noise generator, and a slowly varying

filter representing the vocal tract. Voiced speech is

produced by taking the impulse train as excitation.

In unvoiced segments, the random white noise is

used as the excitation. The output speech is

produced by passing the excitation through the vocal

tract filter. Hence, changes in the vocal tract

configuration, reflected by the filter, produces

corresponding changes in the spectral envelope of

the speech signal. Therefore to estimate the vocal

tract shape form the speech signal, an inverse filter

model has to be used (Miller & Mathews, 1963).

The speech analysis model used in this work is

shown schematically in Figure 1. In this model, it is

assumed that the speech to be analysed is limited to

periodic non-nasalised voiced sounds so that the

filter in Figure 1 is driven by an impulse train. This

means that the filter includes all the contributions

from the glottal wave, the vocal tract and the

radiation impedance at the lips. The inverse filter is

assumed to be a linear filter with only zeros in its

transfer function, and the power spectral envelope of

the speech is assumed to be approximated by poles

only. Accordingly, the transfer function of the

inverse filter can be expressed in terms of z-

transform notation as:

1,)(

∑

−

azazA

(1)

where a

are the coefficients of the inverse filter, M

is the order of the filter,

and T is the

sampling period. Here, a

affects only the gain of the

system, hence no generality is lost by setting

= 1.

The objective of this analysis is to obtain a close

representation of the vocal tract. To obtain this

representation, one needs to estimate the coefficients

of the optimal inverse filter described by equation

(1). Wakita (Wakita, 1973) has shown that A(z) is

also an inverse transfer function of a non-uniform

acoustic tube model of the all-pole vocal tract

model. Thus the optimal inverse filter process in the

above speech analysis model can be equivalently

replaced by a filtering process of an acoustic tube of

length l, which is the assumed length of the vocal

tract, divided into arbitrary number, M, of sections

with equal length

l, provided that:

(a) The continuity conditions for the volume

velocity and sound pressure are satisfied at each

junction between two adjacent sections;

(b) The length of the individual tube sections,

l, are

kept short compared to the wavelength at the

highest frequency of interest;

(d) It should also be noted that the identity of the

filtering process of the above described acoustic

tube to that of the optimum inverse filter is

obtained under the condition

Tjclj

eez

ωω

Δ /2

, where c is the velocity of

sound. Consequently, the sampling frequency F

=1/T and the number of sections M=l/

l is

constrained by (Wakita, 1973):

(2)

Therefore, as long as F

is constant, the vocal

tract length, l, is assumed to be fixed here and M,

i.e. number of the sections or the filter’s order,

has to be chosen to satisfy equation (2).

3 MODELLING THE VOCAL

TRACT

The vocal tract can be modelled as an acoustic tube

of varying diameter. If we abstract from the vocal

tract curvature, the acoustic tube can be divided into

cylindrical sections of equal lengths. Depending on

the shape of the acoustic tube, a sound wave

travelling through it will be reflected in a certain

way so that interferences will generate resonances at

certain frequencies. These resonances are called

formants. Their location largely determines the

speech sound that is heard.

It is well known that the linear prediction (LP)

analysis of speech signals is based on an AR speech

production model (Markel & Gray, 1976). It has also

been shown by several researchers that the LP

process is equivalent to the filtering process of a

non-uniform acoustic tube model where the tube is

divided into an arbitrary number of sections of equal

length (Wakita, 1973; Markovic, 1999). Thus, if the

conditions stated at the end of Section 2 are

satisfied, and if the speech signal is pre-emphasis to

compensate for the spectral characteristics of the

glottal excitation source and for the lips radiation

impedance, then estimates of the vocal tract area

functions can be obtained by computing the

Figure 1: The speech analysis model.

Speech

FILTER

1/A(z)

INVERSE

FILTER

A(z)

Error

−

∑

Impulse

Train

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

154

reflection coefficients at the junctions between

adjacent sections of the equivalent acoustic tube.

This can be done by using an LP model of the

appropriate order and the following relation:

−

=⇔

−

(3)

where A

and A

i+1

are the cross-sectional areas of two

adjacent sections of the non-uniform acoustic tube

indexed in ascending order from the lips to the

glottis, and

is the reflection at the junction

between these two sections.

4 SYSTEM DESIGN AND

DESCRIPTION

Using the vocal tract model described in Section 3, a

PC-based prototype system for visualisation of the

human vocal tract shapes and other associated

speech parameters has been designed and developed.

The system uses the PC’s sound card operating with

8 kHz sampling frequency and 16-bit resolution, to

extract the necessary speech parameters directly

from the acoustic speech waveform. shows The

block diagram given in Figure 2 depicts the

functionality and main processing blocks of the

developed system.

For simplicity, our system uses an initial

assumption that the vocal tract is 17 cm long. As the

PC’s sound card samples the speech at the rate of 8

kHz, thus satisfying equation (2) requires M to be

equal to 8, i.e. the initial use of an acoustic tube with

8 sections. Consequently, an 8

order LP analysis

model is employed by the system.

4.1 Estimation of the Area Functions

The speech signal is segmented into 30 ms frames

using a hamming window of an appropriate length.

A pre-emphasis of an approximately 6 dB/octave is

applied to the current frame using an FIR high-pass

filter of the form:

9375.0

−

−=

nnn

xxy

(4)

The reflection coefficients are computed by applying

an 8

order LP analysis model using an

autocorrelation method that uses LPC uses the

Levinson-Durbin recursive algorithm due to its

simplicity and ease of its implementation within the

chosen computing environment. Equation (3) is then

used to estimate the corresponding vocal tract area

functions as discussed in Section 3. As an example,

Figure 3 (the upper half) shows the normalised area

functions for the English vowel /UH/, as computed

by the system using an 8-section acoustic tube

model. The LP model is also used to obtain the log

spectra, whose peaks are then marked to identify and

estimate the first three formants, as also illustrated in

lower half of Figure 3.

Figure 2: Functional block diagram of the system.

4.2 Mapping to Mid-sagittal Distances

Since the human vocal tract does not resemble an

exact circular tube, there is therefore a need to

modify the above computed area functions such that

they map correctly into mid-sagittal distances of the

vocal tract profiles. Several areas to profile

transformation techniques have been developed

(Heinz & Stevens, 1965). Most such techniques rely

on derivation of suitable application-specific

transformation parameters using complex analysis of

x-ray and cine-fluorograms of various speakers. A

common technique is the αβ model (Heinz &

Stevens, 1965), which is described by:

iiii

ddA

ββ

)( =⇔=

(5)

where A

is the cross-sectional area of a given

section, d

is the mid-sagittal distance and α

and β

are section dependent parameters. In our system, we

Acoustic Speech Signal

Segmentation & Hamming Windowing

Pre-emphasis (High-pass Filter)

LP Analysis (LP Coefficients)

Vocal Tract Areas &

Mid-sagittal

Distance Estimation

Mapping Distances

to Profiles of Vocal

Tract

Estimation of Reflection

Coefficients

Estimation of Log

Spectra

Estimation & Marking of

Formants

2D Mid-Sagittal Vocal

Tract Graphics

X-Y Charts for the

Pitch & Formants

A VOCAL TRACT VISUALISATION TOOL FOR A COMPUTER-BASED SPEECH TRAINING AID FOR

HEARING-IMPAIRED INDIVIDUALS

155

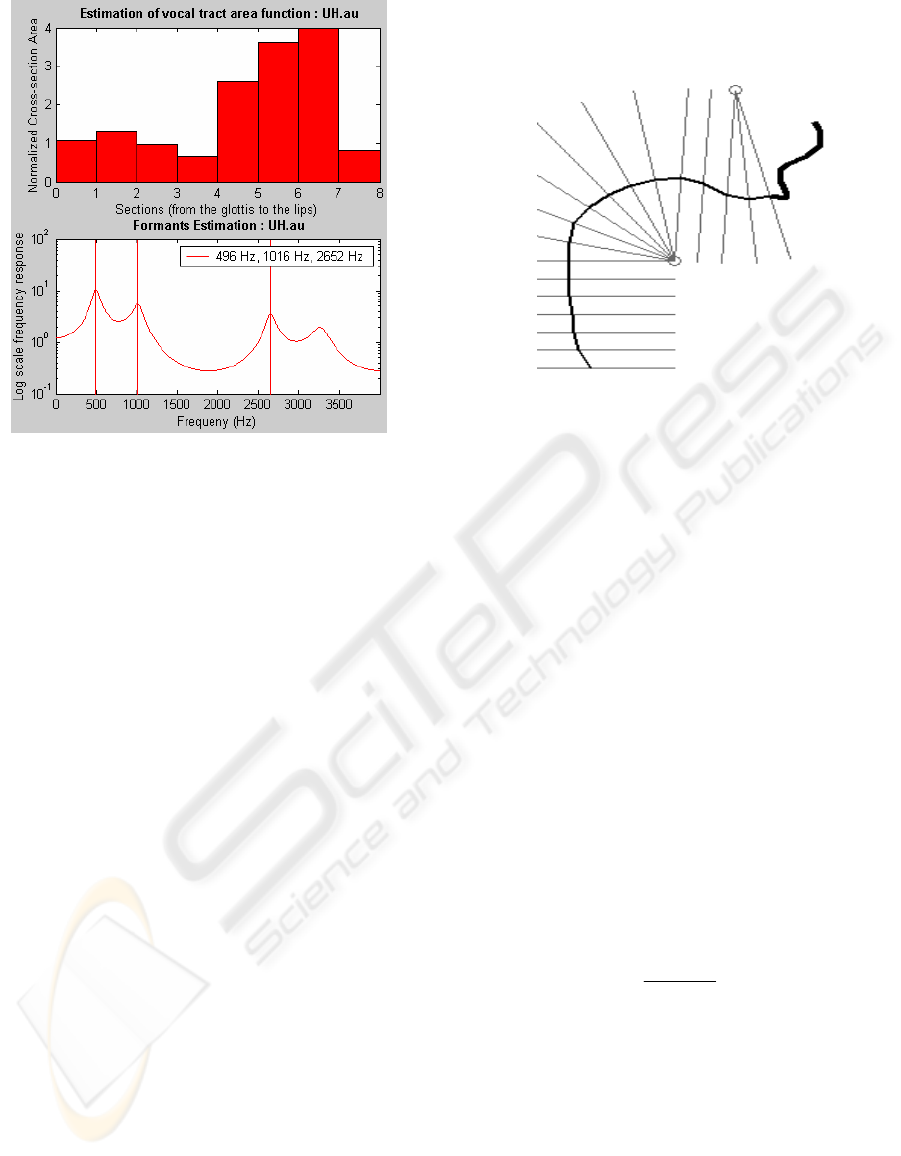
Figure 3: Vocal tract area functions and the first three

corresponding formants for the vowel /UH/.

employ a new method based on the above model to

measure the mid-sagittal distances along the lines of

a semipolar grid (See Figure 4) according to the

following procedure:

(a) The vocal tract was assumed to be divided into

18 equal sections.

(b) In the vocal organs, the shortest path from the

upper to the lower part of each section was

selected.

lower jaw was movable.

(d) A reference grid for the upper jaw based on x-

ray data of the lateral shape of the vocal tract and

on results of the PARAFAC analysis (Harshman,

et. al., 1977) was designed, as shown in Figure 4.

In this grid, straight perpendicular lines were

drawn through the centre of each section, in

accordance with (b) above.

(e) The 8 area functions estimated by the 7th order

LP model were re-sampled and redistributed to

fit the 18-section vocal tract configuration used

in the system.

(f) Based on equation (5), a simple numerical

procedure is used to estimate the values of the

coefficients

and

that minimize the root mean

squared error between the area functions

estimated in (e) above and those derived from

measurement data obtained from (Harshman, et.

al., 1977) for pseudo-sagittal dimensions of the

tongue position for five speakers each saying ten

English vowels. The estimated area functions are

then interrupted as functions of

and

, as given

in equation (5), to compute the mid-sagittal

distances.

Figure 4: The reference upper jaw grid used in the system.

As indicated previously, initially the vocal tract

is modelled in our system with an assumption that it

is 17 cm long. It is known, however, that the vocal

tract length for the utterance of various sounds

varies even for a single speaker. In addition, the

male vocal tract is generally slightly longer than 17

cm, while children and females have shorter vocal

tracts (Kirlin, 1978). Hence, the above assumption

may cause an error in the distribution of the area

functions along the assumed vocal tract

configuration. To compensate for this possible

source of error, the first two mid-sagittal distances

have been determined from the three estimated

formants F

, F

and F

as follows (Ladefoged, et. al.,

1978):

421322211

/3 CFFCFFCFCX +

(6)

where X

is the mid-sagittal distance between the

lips in cm, C

= 0.3×10

-3

, C

= −0.343×10

-6

, C

4.143, C

= −2.865. The mid-sagittal distance

between the upper and lower teeth, X

, is estimated

by:

(7)

where X

is the mid-sagittal distance extracted from

the vocal tract area function that corresponds to

section 3. In addition, the estimated formants have

been used to adjust the rounding degree of the lips

and the height of the jawbone on the designed vocal

tract lateral graphics.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

156

5 RESULTS AND DISCUSSION

The vocal tract visualisation tool has been designed

to operate with MS Windows-based PC

environment. The multi-display window and other

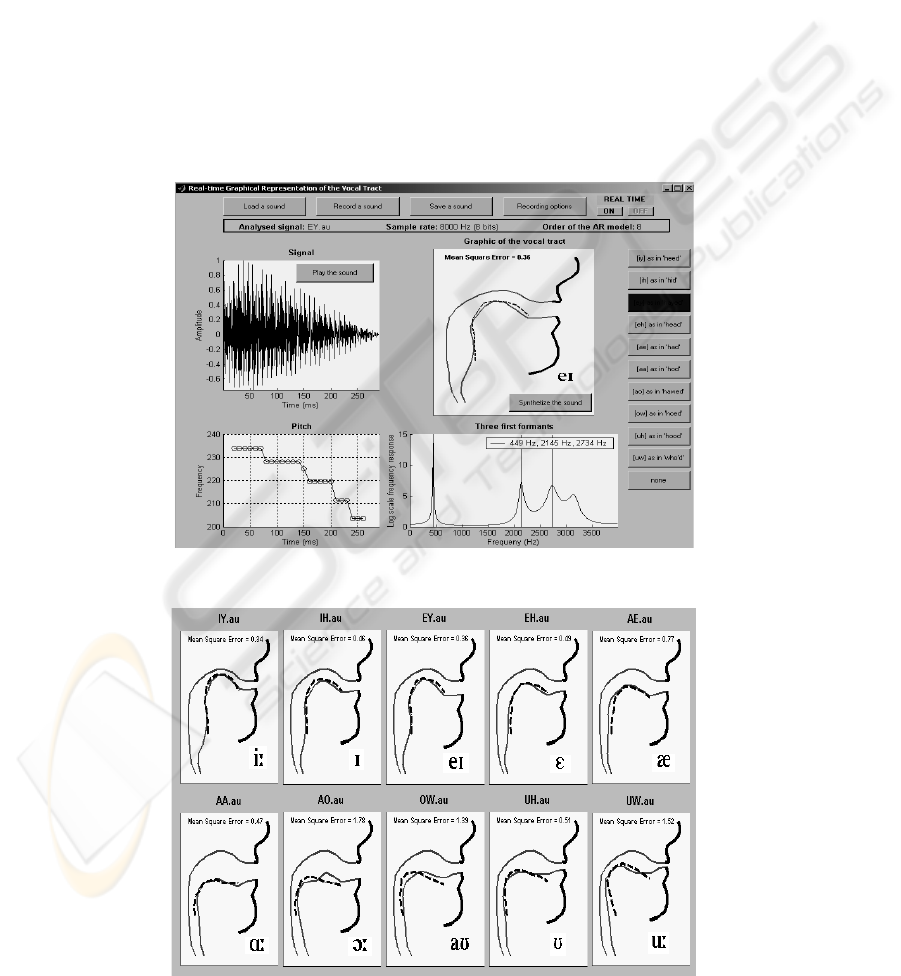
user’s features of the complete system are shown in

Figure 5. As can be seen, the system’s screen is

divided into four windows for displaying the vocal

tract graphics, the sound intensity, the pitch and the

first three formants of the speech signal. The system

can operate in two main modes: (a) near real-time

mode, whereby the speech signal is picked up by a

microphone connected to the PC sound card (as with

the case shown in Figure 5), and (b) non real-time

mode, whereby the speech signal is either recorded

by the system or read from a stored audio file, and

its features are then displayed. It also allows the

saving of speech/sound signals. For the vowel

articulation, the user can compare the shape of

his/hers vocal tract to a reference trace (shown with

a dashed line in Figure 5) for the correct tongue

position derived from the measurements data

reported in (Miller & Mathews, 1963). The

deviation from the reference trace is given for this

case in the form of a computed mean squared error

(MSE) of all the estimated mid-sagittal distances.

Figure 6 shows the vocal tract profiles for 10

American English vowels, as estimated by the

system (dashed lines represent reference trace for

tongue position). For comparison and evaluation

purposes, the deviations, in terms of MSE values,

from the reference tongue position data adopted

from (Harshman, et. al., 1977) are also indicated. In

general, the obtained results seem to correlate well

with the reference data. They were also found to

correlate well with x-ray data and the PARAFAC

analysis. Referring to the MSE values shown in

Figure 6, the system seems to perform particularly

well in the cases of all the ‘front vowels’, such as

/IY/, /EY/, /IH/, /EH/ and /AE/, with the MSE

increasing as the vowel height decreases. With the

exception of /AA/ and /UH/, the results show

relatively less accurate correlation with the reference

data for the cases of the ‘back vowels’. As vowel

classification into front and back vowels is related to

the position of the tongue elevation towards the front

or the back of the mouth, we believe that the higher

accuracy in the cases of the front vowels is attributed

to the formant-based added adjustments of the lips,

jawbone and front sections of the vocal tract we used

in our approach.

On the other hand, the relative length of the

vowel’s vocalisation seems to affect the accuracy of

the estimated area functions and hence the displayed

vocal tract shape. In specific, the system seems to

give relatively lower accuracy for relatively longer

vowels, such as /AO/, and complex vowels which

involve changes in the configuration of the mouth

during production of the sound, such as /OW/. We

believe this is due to the fact that the system, in its

current design, bases its estimation of the speech

parameters on information extracted from the 2-3

middle frames of the analysed speech waveform.

6 CONCLUSIONS

We have described the process of designing and

development of a computer-based system for the

near real-time and non real-time visualisation of the

vocal tract shape during vowel articulation.

Compared to other similar systems, our system uses

a new approach for estimating the vocal tract mid-

sagittal distances based on both the area functions

and the first three formants as extracted from the

acoustic speech signal. It also utilises a novel and

simple technique for mapping the extracted

information to corresponding mid-sagittal distances

on the displayed graphics. The system is also

capable of displaying the sound intensity, the pitch

and the first three formants of the uttered speech. It

extracts the required parameters directly from the

acoustic speech signal using an AR speech

production model and LP analysis. Reported

preliminary experimental results have shown that in

general the system is able to reproduce well the

shapes of the vocal tract, with real-time sensation,

for vowel articulation. Work is well underway to

optimise the algorithm used for extraction of the

required acoustics information and the mapping

technique, such that dynamic descriptions of the

vocal tract configuration for long and complex

vowels, as well as vowel-consonant and consonant-

vowel are obtained. Enhancement of the system’s

real-time capability and features, and facilitation of

an integrated speech training aid for the hearing-

impaired are also being investigated.

REFERENCES

Choi, C.D., 1982. A Review on Development of Visual

speech Display Devices for Hearing Impaired Children.

Commun. Disorders, 5, 38-44.

Bunnell, H.T., Yarrington, D. M. & Polokoff, 2000.

STAR: articulation training for young children. In Intl.

Conf. on Spoken Language Processing

(INTERSPEECH 2000), 4, 85-88.

Mashie, J.J., 1995. Use of sensory aids for teaching speech

to children who are deaf. In Spens , K-E. and Plant, G.

A VOCAL TRACT VISUALISATION TOOL FOR A COMPUTER-BASED SPEECH TRAINING AID FOR

HEARING-IMPAIRED INDIVIDUALS

157

(Eds.), Profound Deafness and Speech

Communication, 461-491, Whurr Publishers Ltd.

Eriksson, E., Balter,, O., Engwall, O., Oster, A-M. &

Sidenbladh-Kjellstrom, H., 2005. Design

recommendations for a computer-based speech

training system based on end-user interviews. In.

SPECOM 2005, 10

Intl. Conf. on Speech and

Computer, 483-486.

Quatieri, T.E., 2002. Discrete-time Speech signal

Processing, Principles and Practice, Prentice Hall.

NJ, USA.

Miller, J.E. & Mathews, M.V., 1963. Investigation of the

glottal waveshape by automatic inverse filtering. J.

Acoust. Soc. Am., 35, 1876-1884.

Wakita, H., 1973. Direct Estimation of the Vocal Tract

Shape by Inverse Filtering of Acoustic Speech

Waveforms. IEEE Trans. on Audio and

Electroacoustics, AU-21, 417-427.

Markel, J. & Gray, A., 1976. Linear Prediction of Speech,

Springer-Verlag. New York, USA.

Markovic, M., 1999. On determining heuristically decision

threshold in robust AR speech model identification

procedure based on quadratic classifier. In ISSPA’99,

Intl. Symp. Sognal Process. And its Applications.

131-134.

Heinz, J.M. & Stevens, K.N., 1965. On the relations

between lateral cineradiographs area functions and

acoustic spectra of the speech. In 5th Int. Congress of

Acoustics. Paper A44.

Harshman, R., Ladefoged, P. & Goldstein, L., 1977.

Factor analysis of tongue shapes. J. Acoustics Soc.

Am., 62, 693-706.

Kirlin, R.L., 1978. A posteriori estimation of vocal tract

length. IEEE Trans. Acoust., Speech, Signal Process.,

ASSP—26, 571-574.

Ladefoged, P., Harshman, R., Goldstein, L., & L. Rice,

1978. Generating vocal tract shapes from formants

frequencies. J. Acoustics Soc. Am., 64, 1027-1035.

Figure 5: System’s multi-pane screen display and user’s extracted features.

Figure 6: Vocal tract profiles for 10 American English vowels as estimated by the system (dashed lines represent reference

traces for tongue positions).

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

158