A NEW METHOD FOR ICG CHARACTERISTIC POINT

DETECTION

Maria Rizzi, Matteo D’Aloia and Beniamino Castagnolo

Dipartimento di Elettrotecnica ed Elettronica – Politecnico di Bari, via E. Orabona, 4 70125 Bari, Italy

Keywords: ICG, C point detection, wavelet transform, parallel filter banks, time frequency analysis, signal processing,

parallel computing

Abstract: Impedance Cardiography is a cost-effective, non-invasive technique particularly useful in measuring cardiac

functions. It evaluates systolic time intervals and stroke volume measuring thorax bioimpedance. In this

paper, adopting the time-frequency analysis method, a new design has been developed to study the first

derivative of impedance cardiography signal. The application of parallel wavelet filter banks has been

investigated and a new method for ICG signal characteristic point detection has been developed. Test results

show the improvement of the method in sensitivity and the feasibility of an easy implementation by design

tools. Moreover, the algorithm noise immunity has been investigated.

1 INTRODUCTION

Impedance Cardiography (ICG) is a technique to

study cardiac functions through measurements of the

thorax electrical impedance. It has been widely

adopted because it is noninvasive, easy to use and

suitable for long-term and continuous monitoring of

hemodynamic function (Jensen, 1995). Moreover,

the ICG signal can be correlated with other

significant signals (i.e. ECG) to generate alarm in

critical situations.

In the past difficulties associated in ICG signal

processing have been motion artefacts, muscle noise,

pacemakers, etc. The most recent ICG devices have

shown improved accuracy. Therefore the ICG has

established a role in the management of outpatients

with hypertension, heart failure and other chronic

diseases (Treister, 2005). The use of ICG in

therapeutic decision making regarding patients with

critical diseases is primarily based on its ability to

identify presence or absence of hemodynamic

abnormalities. For these reasons many researches

have been developed both to study physiological

mechanisms for understanding origin and meaning

of ICG signals and to improve effectiveness and

applicability of ICG diagnostic test adopting

advanced signal processing techniques (Wang,

1995).

Many efforts have been done to implement

automatic detection of reference points in biological

signal. However, existing peak detection algorithms

are difficult to automate for generic use because

either they rely on a number of parameters that need

to be customized for a particular application of the

algorithm or they use reference informations that is

highly specialized for a particular application.

Most of the proposed methods make use of

filtering technique (band pass filtering and temporal

filtering) (Leski, 1992), (Pan, 1984), or adaptive

thresholding technique (Sun, 1992), (Suppappola,

1994). All the previous techniques exhibit

limitations when real signal are adopted (Sun, 2005).

In fact, the first drawback of filtering-based

approach is that frequency variations in the signal

under test (due to different causes such as, for

instance, cardiac frequency changes) may adversely

affect the method performance. For instance, the

frequency band of some biological signal, such as

ECG, differs for different subjects and can change

for the same subject due to particular events. The

second problem in the filter based algorithms is the

frequency band overlapping of noise and some

biological signals. Therefore, the choice of a suitable

bandwidth is a trade off between noise and high

frequency details while the duration of the sliding

window is a trade off between false and missed

detections.

Whereas, the main problem of the thresholding

techniques is their sensitivity to baseline variations

and signal intensity. This high noise sensitivity can

244

Rizzi M., D’Aloia M. and Castagnolo B. (2008).

A NEW METHOD FOR ICG CHARACTERISTIC POINT DETECTION.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 244-249

DOI: 10.5220/0001057802440249

 SciTePress

be a problem for some types of signals having low

signal to noise (S/N) ratio.

An extensive overview of various algorithms for

peak detection in ECG signals can be found in

(Kohler, 2002) which includes approaches based on

neural networks, adaptative filters, Hidden Markov

models and Hilbert transform, too.

The purpose of this paper is to introduce an

improved signal processing technique able to

provide an easy implementation in design tools. It

adopts the wavelet transform for ICG waveform

characteristic point detection. Moreover, for parallel

computing and for implementation by design tool,

parallel filter banks have used in the adopted

technique. Experimental results show the method

validity and its high sensitivity parameter. In fact,

sensitivity reliable results with minimum

interferences from noise and artifact have been

obtained.

2 ICG TECHNIQUE

Impedance cardiography is the study of cardiac

function by means of thorax electrical impedance

measurements. High frequency (20-100KHz), low

intensity current (1-5mA rms) is injected through the

thorax by some electrodes and the impedance

change is sensed by measuring a voltage across

other electrodes. No risk of physiological effects

have been found because various tissues of human

body are not excitable at this frequency and at this

low current level (Patterson, 1989). The impedance

variation can be used for diagnostic information and

for the stroke volume (SV) estimation by using

blood flow appropriate model. The term SV

indicates the amount of blood pumped by the heart

left ventricle in one contraction.

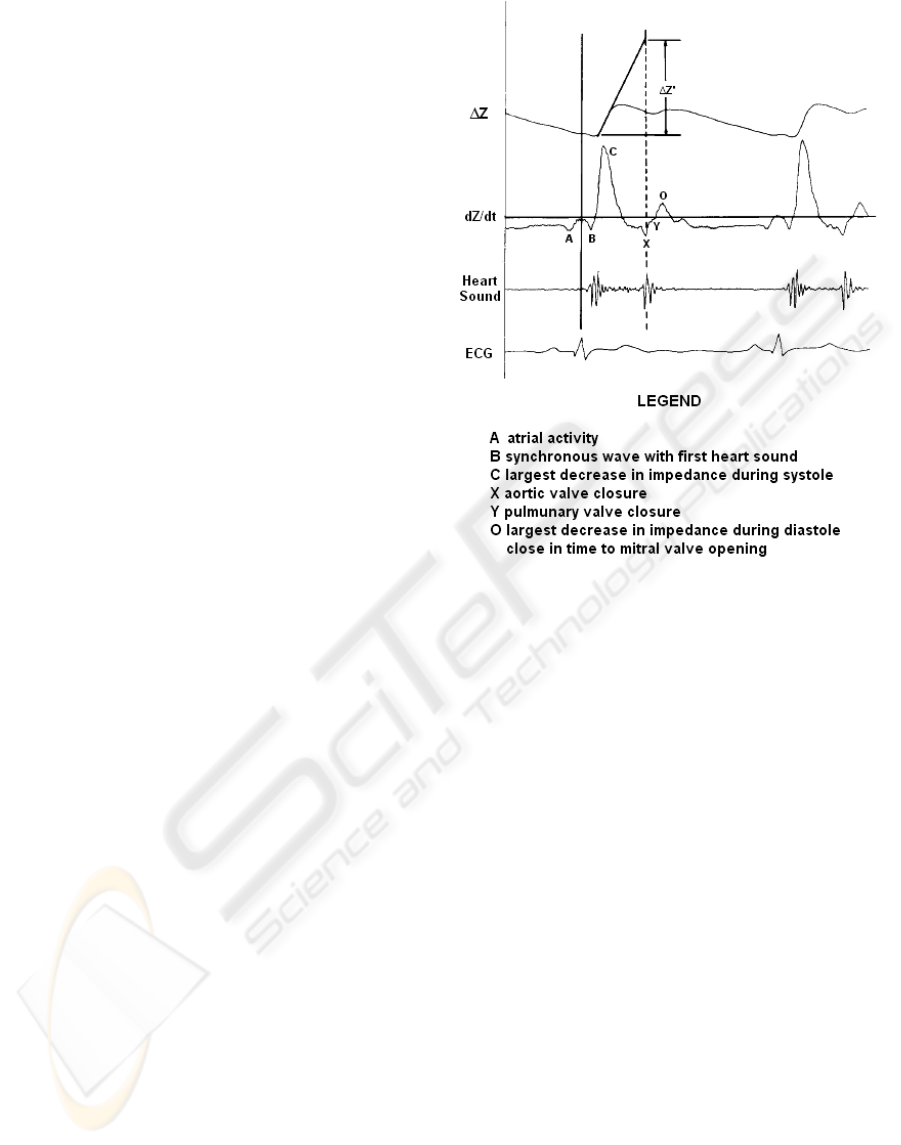
Figure 1 shows a typical impedance waveform

obtained from electrodes in which the characteristic

points are indicated.

Pulsating blood flow through the thoracic aorta

causes shifts in the thoracic impedance as a function

of changes in blood volume. This oscillating

component of the total thoracic impedance can be

expressed as its derivative (dZ/dt). Measurements of

the changes in the thoracic impedance (dZ/dt

waveform) during the cardiac cycle are used to

calculate SV. This can be done in several ways

(Kubicek, 1974), (Sramek, 1982), (Bernstein, 1986).

Generally all the equations take into account

position and value of C-point related to B-point and

X-point.

Figure 1: Typical impedance waveforms from the thorax

of a human subject.

3 WAVELET TRANSFORM

Wavelet transform provides temporal and spectral

information simultaneously, so it is suited for

determining characteristic points of non stationary

and fast transient signals, such as ICG signals. This

feature is suitable to distinguish the ICG signal from

noise and interferences.

The wavelet method decomposes a time variant

signal into several components having various scales

or resolutions. A suitable time and frequency limited

wavelet is chosen as the “mother”. Scaling and

shifting the mother wavelet, a family of functions

called “daughter” wavelet is generated. For small

value of the scale factor, the wavelet is constructed

in the time domain and gives information about fine

details of signals. Therefore a global view of the

signal is obtained by the scale factor large value.

The wavelet transform of a time signal at any scale

is the convolution of the signal and a time-scaled

daughter wavelet.

There are essentially two types of wavelet

decompositions: the redundant ones (continuous

wavelet transform (CWT)), and the nonredundant

ones (orthogonal, semi-orthogonal, or biorthogonal

A NEW METHOD FOR ICG CHARACTERISTIC POINT DETECTION

245

wavelet bases) (Unser, 1996). The first type is

preferable for feature extraction because it provides

for a description that is truly shift-invariant. The

second type is preferable for data reduction, or when

the orthogonality of the representation is an

important factor. However, the choice between these

types of decompositions has to take into account

computational considerations, too. A decomposition

in terms of wavelet bases using Mallat fast algorithm

is typically orders of magnitude faster than a

redundant analysis, even if the fastest available

algorithms are used (Rioul, 1992), (Unser, 1994).

As the aim of this paper is the implementation of

a fast parallelized algorithm, a nonredundant wavelet

decompositions has been chosen. To determine the

best wavelet function to be used, the ICG signal

properties have been studied, such as the shape and

the time localization of events. Temporal signal

shape is an important parameter, so orthogonal

wavelets are unsuitable to be used. In fact they are

unable to provide symmetry in the time domain and

they introduce non-linear phase shift. The signal

shape is maintained if the phase shift is linear. Thus

the wavelet to be adopted should be a symmetrical

function (Dinh, 2001). Spline wavelets have

properties satisfying the previous requirements. The

higher order of the Spline wavelet results in the

sharper frequency response of the equivalent FIR

filter, that is always desirable. But the FIR

equivalent filter of the higher order Spline wavelet

has longer coefficient series leading to more

computational time consumption. Therefore, the

cubic spline wavelet is assumed to have an order

high enough for this application.

Traditional wavelet theory (Cohen, 1996)

considers a decomposition algorithm with an

iterative structure (in particular an asymmetrical tree

structure) that does not efficiently merge with the

novel computational techniques, such as parallel

processing, concurrent programming and design

tools. In this study the a’ trous and the Mallat

algorithms for parallelized filter bank design have

been used (Yang Li, 2005). The algorithm generates

a set of parallelized perfect-reconstruction filter

banks for an arbitrary number of end-nodes of a

traditional tree structure (Koh, 2003).

4 PEAK DETECTOR METHOD

The method presented in this section processes the

first derivate of the impedance signal and allows to

determine the time domain absolute position of C

Peak (figure 1).

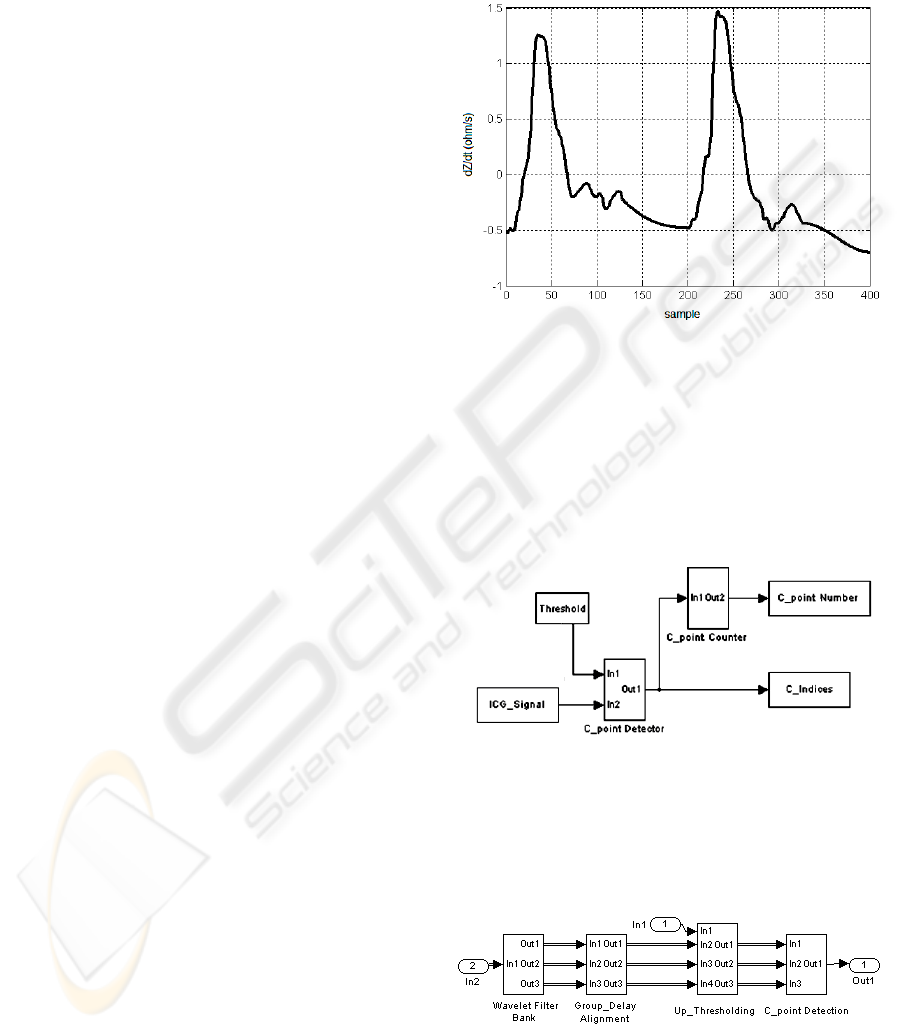
ICG signal (figure 2) is sampled at a frequency of

250 Hz. The input hardware stores sequentially all

the sample in a high speed frame which is then

processed in real time by the system.

Figure 2: ICG signal.

In figure 3 the algorithm model is represented.

The starting signal is indicated with ‘ICG Signal’,

while the results with:

- ‘C_point_Number’ that evaluates the number of

peaks presents in the processed frame;

- C_Indices’ whose aim is the determination of

the position of samples which corresponds to peaks

Figure 3: Algorithm model realized with the software tool

MATLAB Simulink

®.

The ‘C_point Detector’ subsytem (figure 4)

determines the ICG signal peaks.

Figure 4: ‘C point detector’ subsystem model.

It uses an evolution of the classical Mallat

decomposition, called a’ trous algorithm. The a’

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

246

trous algorithm for non-ortogonal wavelet uses a

filter bank structure as the Mallat algorithm (Mallat,

1989), but differs only for the filters design. It has

been demonstrated that after the application of

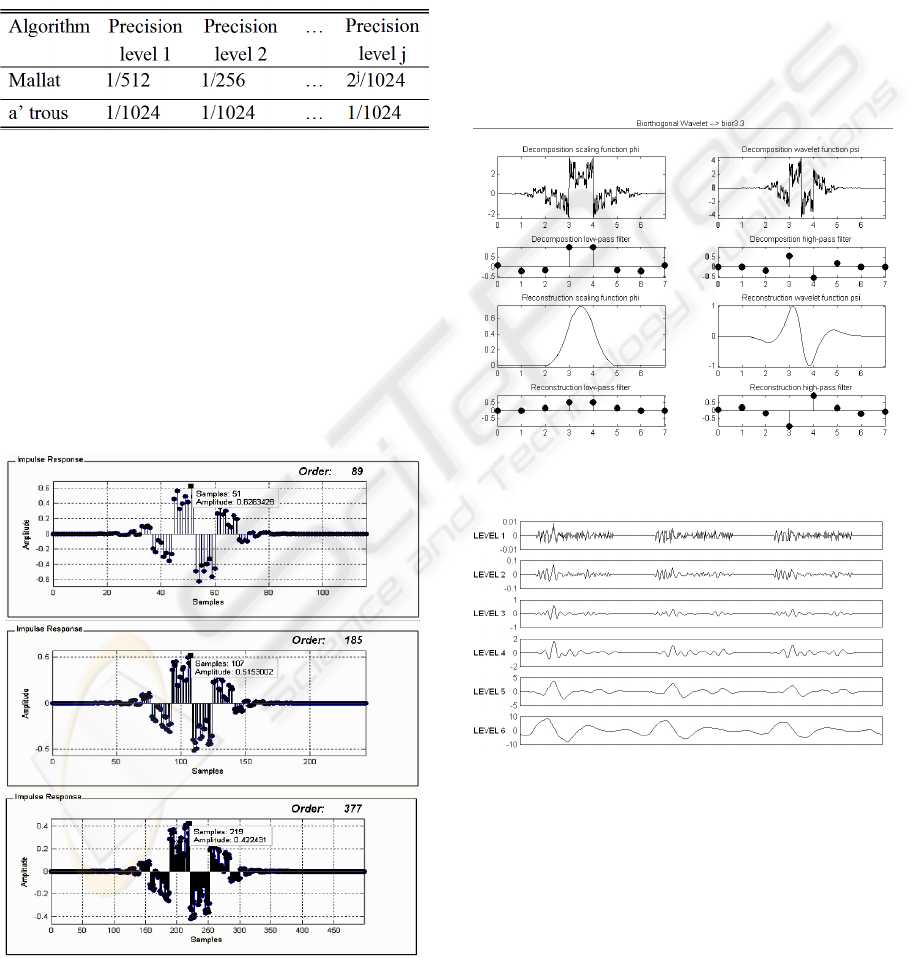
wavelet filters for j-times, the precision of a’ trous

algorithm is 2j time higher then the Mallat algorithm

(Table 1) (Shensa, 1992).

Table 1: Precision of Mallat algorithm and a’ trous

algorithm varying decomposition level

For the tree structure of the algorithm, the

previous structure is not suitable for parallel

computing and for implementation in design tools.

To overcome this limit equivalent parallel filter

banks have been used. As it is known, the output

signal realignment is necessary only to put just the

delay introduced by each filter (figure 5).

A cubic spline wavelet (wavelet ‘bior3.3’) has

been chosen because it makes possible the perfect

signal reconstruction (figure 6).

For ICG signal processing, six dyadic scales

have been used to decompose the signal (figure 7).

Figure 5: Pulse response of FIR filters equivalent to levels

4, 5, 6.

With a soft treesholding technique applied to

level 1, 2, 3, the noise has been reduced and then the

signal reconstructed in the time domain.

To localize characteristic points inside signal,

detail levels 4, 5, 6 have been considered because

they contain the highest number of C signal

frequencies.

In respect to each singularity in ICG signal, a

point of maximum value in detail coefficient signal

is present. The proposed method searches local

maximum points in the positive region of scale 4,

scale 5 and scale 6 using a thresholding technique.

Various tests have indicated the local maximum in

the lower scale as the best points for the real signal

peak localization

Figure 6: Wavelet ‘bior3.3’.

Figure 7: Decomposition of ICG signal over six scales.

5 RESULTS AND DISCUSSION

Real ICG signal (fig.8) has been tested with good

results. Moreover the test has been repeated adding

Gaussian noise with zero average and variable

variance. In this situation the algorithm noise

immunity has been evaluated.

A NEW METHOD FOR ICG CHARACTERISTIC POINT DETECTION

247

Figure 8: Frame tested.

The software detection algorithms for medical

applications requires the evaluation of the detection

performance according to ANSI/AAMI standard.

Two parameters are used to evaluate algorithms:

Sensitivity:

FNTP

(1)

Positive Prediction:

FpTP

(2)

where:

 TP is the number of true positive detections;

 FN (the number of false negatives) is the

number of C points present in the signal that the

algorithm is not able to detect;

 FP (the number of false positives) is the number

of C points detected by the algorithm but really

not present in the signal.

Tested Frame presents C-peak value fluctuations

in the range [1÷1.5Ω/s]. Other local maximum

points are all in the negative region. Algorithm has

individuated the 50% of the maximum value of the

wavelet in each windowed segment of data as the

optimal threshold value.

The obtained sensitivity parameter is very

satisfactory and appears quite independent from

noise (figure 9). Predictivity is fairly good but

decreases as noise increases (figure 10).

Anyway it is to be noted that very heavy noise

conditions have been chosen to test the algorithm

noise immunity. An additional Gaussian noise signal

with v=0.1(Ω/s)

corrupts heavily the ICG signal; in

particular the noise, besides changing the ICG signal

shape, introduces many false peaks while cancels a

minor number of true peaks.

Figure 9: Sensitivity.

Figure 10: Positive Predictivity.

6 CONCLUSIONS

The real-time C-point detection algorithm presented

in this paper has demonstrated to have high

sensitivity.

The method computational time has been

optimized adopting a parallel procedure to analyze

the ICG signal. Therefore the realized procedure is

suited to be implemented in real applications.

Practical performance is to be improved for positive

predictivity that appears to be sensible to noise level.

Moreover, the absence of standard and validated

ICG data bases, such as those used for ECG signals,

makes the algorithm efficiency evaluation difficult

and provides results poorly reproducible and

comparable.

REFERENCES

Bernstein, D. P. (1986). A new stroke volume equation for

thoracic electrical bioimpedance: theory and rationale.

Critical Care Medicine, 14(10), 904-909

Cohen, A., Kovacevic, J. (1996). Wavelets: the

mathematical background. Proceedings of the IEEE,

84, 514-522

Dinh, H. A. N., Kumar, D. K., Pah, N. D., & Burton, P.

(2001). Wavelets for QRS detection. Proceedings of

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

248

the 23rd Annual International Conference of the IEEE

Engineering in Medicine and Biology Society, 2, 1883-

1887.

Jensen, L., Yakimets, J., & Teo, K.K. (1995). A review of

impedance cardiography. Heart & Lung, 24, 183-193

Koh, M. S., & Rodriguez-Marek, E. (2003). Generalized

and parallelized ´a trous and Mallat algorithms to

design non-uniform filter-banks. Proceedings of the

IEEE International Symposium on Signal Processing

and Information, Darmstadt, Germany, 38-41.

Kohler, B.U., Hennig, C., & Orglmeister, R. (2002). The

principles of software QRS detection. IEEE Eng. in

Medicine and Biology, 2, 42-56

Kubicek, W. G., Kottke, F. J., Ramos, M. U., Patterson, R.

P., Witsoe, D. A., Labree, J. W., et al. (1974). The

Minnesota impedance cardiograph, theory and

applications. Biomedical Engineering, 9, 410-416

Leski, J., & Tkacz, E. (1992). A new parallel concept for

QRS complex detector. Proceedings of the 14th

Annual International. Conference. IEEE Eng. in

medicine and Biology Society, part 2 , Paris, France,

555-556

Mallat, S. G. (1989). A theory for multiresolution signal

decomposition: the wavelet representation.

Transactions on Pattern Analysis and Machine

Intelligence, 11, 674-693

Pan, J., & Tompkins, W.J. (1984). A real-time QRS

detection algorithm. IEEE Trans. Biomed. Eng., 22,

289-297

Patterson, R. P. (1989). Fundamentals of impedance

cardiography. IEEE Engineering in Medicine and

Biology Magazine, 8, 35-38

Rioul, O., & Duhamel, P. (1992). Fast algorithms for

discrete and continuous wavelet transforms. IEEE

Trans. Information Theory, 38(2), 569-586

Shensa, M.J. (1992). The discrete wavelet transform:

wedding the a’trous and Mallat algorithms. IEEE

Trans. on signal processing, 40, 2464-2482

Sramek, B. B. (1982). Cardiac output by electrical

impedance. Medical Electronics, 4, 93-97

Sun, Y., Chan, K. L, & Krishnan, S. M. (2005).

Characteristic wave detection in ECG signal using

morphological transform. BMC Cardiovascular

Disorders, 5, 28

Sun, Y., Suppappola, S., & Wrublewski, T.A. (1992).

Microcontroller-based real-time QRS detection.

Biomed. Instr. Technol., 26, 313-327

Suppappola, S., & Sun, Y. (1994). Nonlinear transforms of

ECG signals for digital QRS detection: A qualitative

analysis. IEEE Trans. Biomed. Eng., 41, 397-400

Treister, N., Wagner, K., & Jansen, P.R. (2005).

Reproducibility of impedance cardiography

parameters in outpatients with clinically stable

coronary artery disease. American Journal of

hypertension, 18, 44-50

Unser, M. (1994). Fast Gabor-like windowed Fourier and

continuous wavelet transforms.

IEEE Signal

Processing Letters, 1(4), 76-79

Unser, M., & Aldroubi A. (1996). A review of wavelets in

biomedical application. Proceedings of the IEEE,

84(4), 626-638

Yang, Li Y., Chenglin, P., Huafeng, W., Zhiqiang, Z., &

Min, M. (2005). Using a’trous Algorithm and

Modulus Maximum Lines to Detect R-wave of ECG

Signal. Proceedings of the 27th Annual Conference of

the IEEE Engineering in Medicine and Biology,

Shanghai, China, 1270-1273.

Wang, X., Sun, H., & Van De Water, J. M. (1995). An

advanced signal processing technique for impedance

cardiography. IEEE Trans. on Biomedical

Engineering, 42, 224-230.

A NEW METHOD FOR ICG CHARACTERISTIC POINT DETECTION

249