PHASE SEGMENTATION OF NOISY RESPIRATORY SOUND
SIGNALS USING GENETIC APPROACH
Feng Jin, Farook Sattar
School of Electrical & Electronic Engineering, Nanyang Technological University
Nanyang Avenue, Singapore 639798
Moe Pwint
Dept. of Information Science, The University of Computer Studies, Yangon, Myanmar
Keywords:
Noisy Respiratory Sound Signals, Phase Segmentation, Sample Entropy(SampEn), Genetic Algorithm (GA).
Abstract:
In this paper, a new approach to automatically segment noisy respiratory sound signals is proposed. Segmen-
tation is formulated as an optimization problem and the boundaries of the signal segments are detected using
a genetic algorithm (GA). As the estimated number of segments present in a segmenting signal is initially
obtained, a multi-population GA is employed to determine the locations of segment boundaries. The seg-
mentation results are found through the generations of GA by introducing a new evaluation function, which
is based on the sample entropy and a heterogeneity measure. Illustrative results for respiratory sound signals
contaminated by loud heartbeats and other high level noises show that the proposed genetic segmentation
method is quite accurate and threshold independent to find the noisy respiratory segments as well as the pause
segments under different noisy conditions.
1 INTRODUCTION
Respiratory rate (RR) monitoring plays an important
role in many clinical situation. Correct timing of in-
dividual respiratory phases can be useful in study-
ing flow in the heart (Hult et al., 2000), quantify-
ing adventitious respiratory sounds and many other
situations. Different airflow measurements, such as
mouthpiece pneumotachograph or chest movement
measurement, are the most widely applied methods
in monitoring RR and respiratory phases. However,
it would be difficult to apply such methods under cer-
tain circumstances, especially when studying children
with neurological impairments (Yadollahi and Mous-
savi, 2006). Hereby, acoustical analysis of respiratory
sounds has recently provided an alternative way to de-
tect respiratory phases and therefore RR.
Tracheal breath sound refers to respiratory sound
recorded over suprasternal notch. It can be segmented
into four successive phases: inspiratory phase, expi-
ratory phase, end-inspiratory pause, expiratory phase,
and end-expiratory pause. It is chosen due to its
distinct phases and relatively larger amplitude com-
pared with sounds recorded over chest, as well as
its close relationship to respiratory flow. A few at-
tempts have been done to estimate flow for segmen-
tation through tracheal sounds in the past. Among
all, one of the effective method is the signal analy-
sis approach uses the temporal and frequency vari-
ables of tracheal sounds as well as disturbance char-
acteristics (Hult et al., 2000). It is able to identify
different respiratory phases but it requires more than
one microphone to capture the ambient noise and it
is sensitive to disturbance. To avoid such problems,
in (Yadollahi and Moussavi, 2006), flow estimation
using Shannon entropy of the bandpass filtered tra-
cheal sounds is proposed.
Both the above mentioned methods are generally
effective on preprocessed tracheal sounds which are
free of heartbeats and ambient noise. However heart-
beat as one of the most influential noise for respi-
ratory sounds are usually unavoidable during signal
recording. It has the frequency range of [0 300]Hz
which interferes with that for respiratory sounds; and
it masks the respiratory sounds because of its high
intensity. When the recorded signals which are cor-
rupted by heartbeats or other unknown types of high
level noises, the segmentation becomes tough and
thus it is difficult to locate the boundaries of respi-
ratory phases accurately. To deal with this problem, a
122
Jin F., Sattar F. and Pwint M. (2008).
PHASE SEGMENTATION OF NOISY RESPIRATORY SOUND SIGNALS USING GENETIC APPROACH.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 122-127
DOI: 10.5220/0001058001220127
Copyright
c
 SciTePress

genetic algorithm (GA) is employed for the first time
to segment accurately the noisy respiratory signal.
The aim of this paper is to propose an genetic al-
gorithm for automatic phase segmentation of respi-
ratory sounds corrupted by heartbeats and other un-
known types and levels of noises. The segmentation
method described here is based on a stochastic global
search method. To guide the search space of generic
algorithm, an evaluation function combined sample
entropy and heterogeneity measure is introduced.
2 GENETIC ALGORITHM BASED
RESPIRATORY PHASE
SEGMENTATION
As for our phase segmentation, the locations of the
segment boundaries are detected using our genetic al-
gorithm. Depending on the total number of segments
as prior information or estimated using any existing
technique(e.g. using an onset detection algorithm),
an initial population is randomly generated.
To guide the search space of GA, a new eval-
uation function is introduced. First the irregularity
in the time series (i.e. input sequence) is investi-
gated using sample entropy (SampEn). Measuring
the homogeneity and heterogeneity of the candidate
segments, the fitness of the evaluation function is de-
signed. Through the generations of GA, the locations
of segment boundaries are then optimized.
2.1 Sample Entropy
In this GA based segmentation method, a similarity
measure of times series (sample entropy) is employed
to determine the boundaries of respiratory segments.
Sample entropy (SampEn) is applied here to measure
the complexity and regularity of time series signals’
similarities. SampEn(m, r, N) is chosen as it does not
count self-matches of the time series. This ensures the
consistency of the measurement and reduces the de-
pendency on the signal length. It is defined in (Rich-
man and Moorman, 2000) as the negative natural log-
arithm of the conditional probability that a data set of
length N, having repeated itself within a tolerance r
for m points, will also repeat itself for m + 1 points,
without allowing self-matches.
For an input signal u of length N, {u( j) : 1 ≤ j ≤
N} forms the N − m + 1 vectors x
m
(i) for {i|1 ≤ i ≤
N − m+ 1}, where x
m
(i) = {u(i+ k) : 0 ≤ k ≤ m− 1}
is the vector of m data points from u(i) to u(i+m−1).
In this context, only the first N − m vectors of length
m are considered to ensure that, x
m
(i) and x
m+1
(i) are
defined for 1 ≤ i ≤ N −m. Let B
m
(r) is the probability
that two sequences will match for m points and A
m
(r)
is the probability that two sequences will match for
m+1 points. B
m
i
(r) is defined as (N − m− 1)
−1
times
the numbers of vectors x
m
( j) within r of x
m
(i), where
1 ≤ j ≤ N − m, and j 6= i to exclude self-matches.
Then B
m
(r) is defined as
B
m
(r) = (N − m)
−1
N−1
∑
i=1
B
m
i
(r) (1)
Similarly, A
m
i
(r) is defined as (N − m − 1)
−1
times
the numbers of vectors x
m+1
( j) within r of x
m+1
(i),
where 1 ≤ j ≤ N − m and j 6= i. Then set A
m
(r) as
A
m
(r) = (N − m)
−1
N−1
∑
i=1
A
m
i
(r) (2)
Finally, sample entropy (SampEn) is calculated by
SampEn(m,r, N) = −ln
A
m
(r)
B
m
(r)
(3)
SampEn measures the regularity of data sequence.
A low value of SampEn reflects a high degree of self-
similarity in time series. With increasing irregularity,
a larger value of SampEn is obtained. The SampEn
increases for respiratory segments and decreases dur-
ing the appearance of pause segments. Hence, the
dynamics of segmenting respiratory signal can be in-
vestigated through the sample entropy sequence. And
sample entropy can be applied as a useful tool to de-
termine the locations of the respiratory segments as
well as pause segments for a noisy respiratory sound
signal.
2.2 Genetic Algorithm
GAs are numerical optimization algorithms inspired
by both natural selection and natural genetics (Coley,
2001). GAs operate on a population of strings, that is,
a group of potential solutions of a problem. To mea-
sure how good or bad the solutions within the popu-
lation, fitness of each string is calculated in decoded
form (solution vector) applying an evaluation func-
tion. At each generation, a new set of solutions are
produced by selecting the fittest strings in the prob-
lem domain and through the application of the genetic
operators such as crossover and mutation. A review
for the fundamental operations of a simple GA can be
found in (Tang et al., 1996). The procedure of a sim-
ple GA can be described as follows, where the pop-
ulation of candidate solutions at time t is represented
by P(t):
PHASE SEGMENTATION OF NOISY RESPIRATORY SOUND SIGNALS USING GENETIC APPROACH
123

begin
t = 0;
initialize P(t);
while not termination criteria do
begin
t = t + 1;
select P(t) from P(t-1);
reproduce pairs in P(t);
evaluate P(t);
end
end
2.2.1 Initial Population
In order to detect both start and end locations of each
segment, a population of GA is generated with strings
whose length is two times the total number of seg-
ments as obtained earlier. A string is a real-valued
string representing the locations of the candidate seg-
ment boundaries in increasing order. Although the
binary-coded GAs are the most commonly used rep-
resentation, a more natural real-valued representation
is used in this system to increase the efficiency of GA.
Using the real-valued strings, there is no need to con-
vert strings to solution vectors to evaluate their fitness.
Thus it would be faster in computation.
2.2.2 Evaluation Function
In GAs, an evaluation function or fitness function is
usually used to evaluate the performanceof the strings
in the problem domain. In order to obtain accurate
boundaries of each segment, an evaluation function is
designed using the heterogeneity measure and sample
entropy. This function simultaneously maximize the
homogeneity within the segments and heterogeneity
among different segments using sample entropy.
In this context, SampEn of the original segment-
ing signal is calculated first to investigate the dynam-
ics. To prevent the requirement of large computa-
tional time (to obtain the feasible computation time
and to make the proposed algorithm to be tractable),
SampEn is calculated on each data set of length 100
(i.e. N=100) within a tolerance r of 0.15 × SD for 1
point (i.e. m=1). Here, SD is the standard deviation of
the data set. Let H
w
be the total within-segment ho-
mogeneity and H
b
denotes the total between-segment
heterogeneity, a segmentation evaluation function is
defined as
H =
H
b
+ 1
H
b
+ H
w
+ 1
(4)
where total within-heterogeneity H
w
is defined as
H
w
=
S
∑
i=1
L
i
σ
2
i
L
(5)
where L is the total length of the segmented signal,
L
i
is the length of i-th segment, σ
2
i
is the variance of
the sample entropy of the i-th segment and S is the
number of segments in the segmented signal. The
between-segment heterogeneity, H
b
, is defined as the
average Euclidean distance between the mean value
of the sample entropy of any two adjacent segments.
H
b
=
∑
(i, j)∈ad jacent,i6= j
kµ
i
− µ
j
k
2
ns
(6)
where ns is the total number of the adjacent segments
in the segmented signal, µ
i
and µ
j
are the mean value
of the sample entropy of the i-th and j-th segments.
H becomes one when the internals of all segmented
respiratory signals are completely homogeneous.
2.2.3 Evolution Procedure
In order to effectively search the solution space, and
to take advantage of the parallelism of GAs, the pro-
posed algorithm applies the multiple subpopulations
approach provided by (Chipperfield et al., 1995) for
the evolutionary process. Using multiple populations
the quality of the results obtained can be improved
compared to GAs with single population. This ap-
proach divides the population into a subpopulations
where each of them can evolve independently using
parallel processing technique. It can search in parallel
different subspaces of the search space, thus making
it less likely to become trapped by low-quality sub-
spaces. Multiple populations GA is a widely used par-
allel GA model where multiple subpopulations evolve
independently toward different optima. More diverse
subpopulations can be maintained by exchanging ge-
netic materials between subpopulations. The prema-
ture convergenceeffect of simple GA can then be mit-
igated by this approach. To reduce the required com-
putational time, it is implemented through the use of
high-level genetic operator functions and exchanging
individuals between subpopulations.
Over generations, each subpopulation is evolved
as in traditional simple genetic algorithm (SGA) us-
ing the basic operators: crossover and mutation. De-
pending on the migration interval (i.e. the number
of generations between successive migration) and the
migration rate (i.e. the number of individuals to be
migrated from one subpopulation to another), individ-
uals from one subpopulation migrate to another from
time to time. The initial population is created using
8 subpopulations containing 20 individuals each. At
each generation, 90% of the individuals with higher
fitness values within each subpopulation are selected
for breeding using a stochastic universal sampling
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
124

function which has minimum spread and zero bias.
In GAs, the recombination operator is usually
used to produce the new offsprings. By applying dis-
crete recombination crossover, a uniform crossover
for real-valued representation, the new offsprings
within each subpopulation are produced. Normally,
offsprings are mutated after recombination to prevent
the population from converging to local minima. And
the new possible solutions can be introduced to the
population by mutating the offsprings. In this system,
a mutation rate of 1/nvar is used, where nvar is the
length of an individual.
When the offsprings produced are less than the
size of the original population, the new offsprings
have to be reinserted into the population to maintain
the size of the original population. Similarly, when
not all the offsprings are to be used at each generation,
or if the offsprings produced are more than necessary,
a reinsertion scheme must be used. This scheme de-
termines which individuals should be replaced by the
offsprings produced and which individuals should be
inserted into the new population.
In this segmentation method, offsprings are in-
serted into the appropriate subpopulations depending
on fitness-based reinsertion with a rate of 0.9. In this
multi-population GAs, migration of individuals be-
tween subpopulations is performed at every 20 gener-
ations with a migration rate of 0.2. After GA iterates
for maxgen times (here maxgen=80), the evolution of
this GA stops. The best individual with the maximum
fitness value presents the optimized solution for the
boundaries of the segments of the segmented signal.
3 SIMULATION RESULTS
In this section, performance of the method is
presented for the noisy respiratory sound signals.
Both the standard preprocessed normal tracheal
breath sound from (Lehrer, 2002; Tilkian and
Conover, 2001; R. L. Wilkins and Lopez, 2004)
and normal recorded data as corrupted with heart-
beats(Phonocardiogram,PCG) and ambient noise, are
used to test the segmentation method.
3.1 Acquisition of Respiratory Sounds
The recording environment and equipments are cho-
sen based on the standard given by (Rossi et al.,
2000). Short-term recordings have been done in sit-
ting position in audio laboratory which provides a
quiet environment. One electret condenser micro-
phone (ECM-77, Sony, Inc., Tokyo, Japan) has in-
serted into a hemispherical rubber chamber 2cm in
diameter, and placed at suprasternal notch of the test
subjects to record the tracheal breath sounds. Record-
ing software WAVEPAD (V3.05, NCH Swift Sound
Software) has been used and the signal clips have
been recorded and saved as mono-channel *.wav file
at sampling frequency of 8 kHz. Test subjects have
been asked to breath normally, and 20s recording are
saved each time.
3.2 Test Respiratory Data
Tracheal breath sounds signals from 10 healthy stu-
dents of Nanyang Technological University have been
used as the dataset of the performance test. The sam-
ple size of 10 consists of 6 females and 4 males,
each producing two clips of 20s recording. All clips
have been testified to be normal tracheal breath by Dr.
Daniel Goh from National University Hospital of Sin-
gapore.
3.3 Results
This section presents the simulation results using
noisy respiratory sound signals. Four different exam-
ples regarding segmentation of normal noisy breath
sounds are given below. The sampling frequency used
is 8 kHz.
Example 1: In this example, the segmentation re-
sults for a normal infant tracheal sound from the stan-
dard data set, are demonstrated. In contrary to the
existing phase segmentation methods, the proposed
method is able to function with the presence of heart-
beats and provides accurate segmentation results at
different levels of PCG (varying with a scaling factor
of α)(See Fig. 1). Fig. 1(a) shows the segmentation
result for 3 cycles of infant tracheal breath, whereas
Figs. 1(b)-(c) show the results with the superimposed
PCG. Comparing the results in Fig. 1, it is found that
the present method performs well irrespective of PCG
level without using any threshold parameter.
Example 2: In this example, segmentation results
for the recorded adult normal tracheal breath sound
are shown. Both the original signal and the noisy
recorded signal interfered with heartbeats, are con-
sidered here for illustration. Unlike the infant breath
(Fig. 2(a)), the adult breath in Fig. 2(a) has differ-
ent time evolution (i.e. slower respiration rate) and
shallow. The segmentation results in the presence of
heartbeats are still found effective like the previous
case.
Example 3: In this example, segmentation results
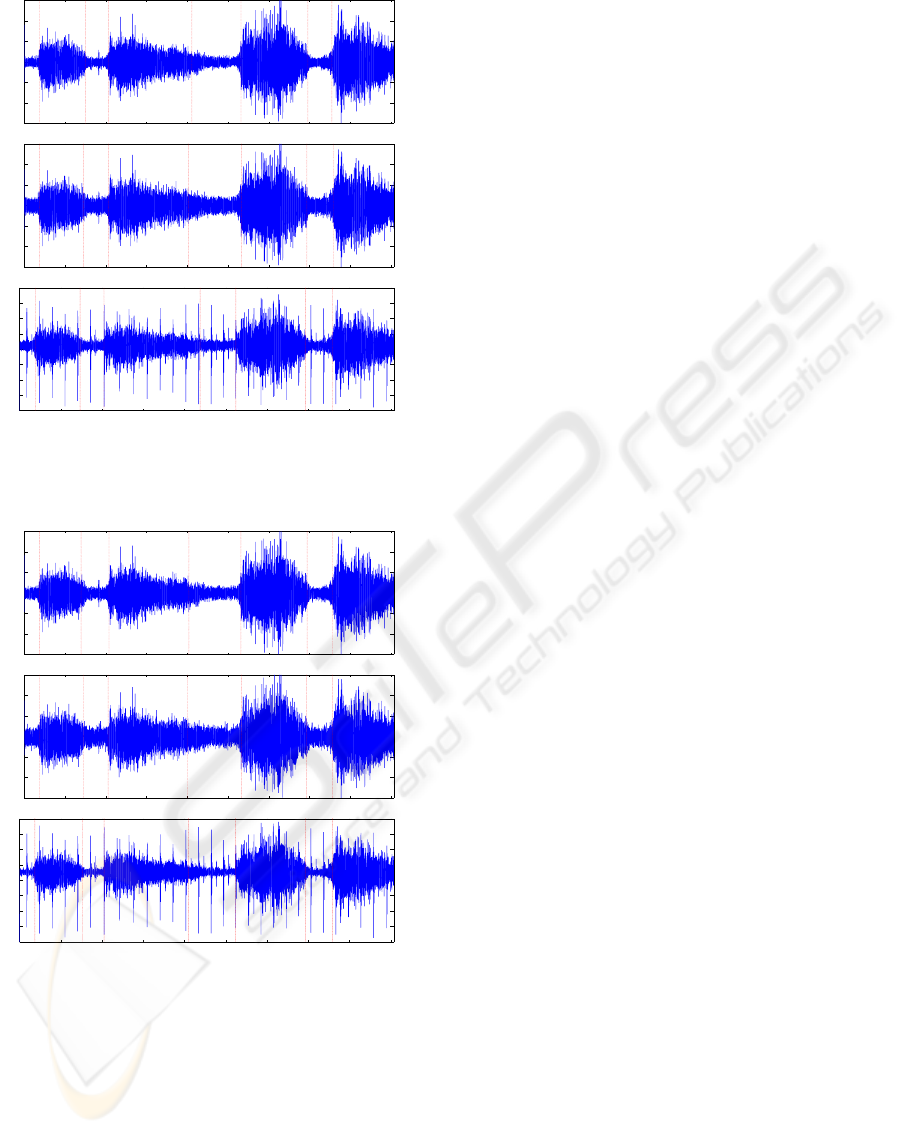
are shown for a signal of noisy recorded respiratory
sound due to background White Noise (WN) of vary-
ing noise variance as ambient noise (see Fig. 3(a)-
PHASE SEGMENTATION OF NOISY RESPIRATORY SOUND SIGNALS USING GENETIC APPROACH
125

0 0.5 1 1.5 2 2.5 3
x 10
4
−0.5
−0.4
−0.3
−0.2
−0.1
0
0.1
0.2
0.3
0.4
0.5
Results for original infant breath sound
Sample
0 0.5 1 1.5 2 2.5 3
x 10
4
0
0.2
0.4
0.6
0.8
1
Sample
Results for original infant breath superimposed with PCG sound
0 0.5 1 1.5 2 2.5 3
x 10
4
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
Results for original infant breath superimposed with PCG sound
Sample
(a)
(b)
(c)
Figure 1: Segmentation results of the standard infant tra-
cheal breath sound: (a) without PCG sound; (b)-(c) with
PCG sound added with scaling factor α=1 and 2, respec-
tively.
(b)). Also, simulation result in the presence of both
white noise and PCG (heartbeats) is illustrated in Fig.
3(c). As it is seen in Fig. 3 that the segmenation
method provides good results for white background
noise and heartbeats.
Example 4: In this example, segmentation results
are presented, Fig. 4(a)-(b), for the noisy recorded
signal corrupted by background Colored Noise (CN)
with varying noise level. Also, a simulation example
for both ambient colored noise and PCG interference
is shown in Fig. 4(c). The colored noise is realized
as EEG noise, v(n), which is simulated by an ARMA
process described as v(n) =
C(z
−1
)
A(z
−1
)
e(n) where e(n) is
the zero-mean white Gaussian noise and C(z
−1
) and
A(z
−1
) are third-order polynomials in the backward
shifting operator z
−1
. The coefficents of C(z
−1
) and
A(z
−1
) are chosen in a way that makes the spectrum
of the ARMA precess approximates the EEG process.
The estimation error is defined as
ε =
1
N
N
∑
n=1
|
P
n
est
− P
n
ref
P
n
ref
| (7)
where P
n
est
is the starting/ end position of the nth seg-
ment for a noisy signal and P
n
ref
is that for a prepro-
cessed signal without white noise, colored noise, and
0 1 2 3 4 5 6 7 8 9
x 10
4
−0.5
−0.4
−0.3
−0.2
−0.1
0
0.1
0.2
0.3
0.4
0.5
Segmentation of Recorded Signal
Sample
0 1 2 3 4 5 6 7 8 9
x 10
4
−0.4
−0.3
−0.2
−0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
Sample
Segmentation of Noisy Recorded Signal (Superimposed PCG with scaling factor 0.25)
0 1 2 3 4 5 6 7 8 9
x 10
4
−0.2
−0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
Segmentation of Noisy Recorded Signal (Superimposed PCG with scaling factor 0.5)
Sample
(a)
(b)
(c)
Figure 2: Segmentation results of: (a) preprocessed
recorded tracheal breath sound; (b) original recorded tra-
cheal breath sound with heartbeats; (c) recorded tracheal
breath sound with superimposed PCG for scaling factor
α=0.5.
PCG. For performance of segmentation method on
real Recorded Tracheal Sound (RTS) with different
types of noises imposed onto it as indicated in Figs. 2-
4, the error is calculated for each subject using Eq. 7
and then averaged between the subjects.
Table 1: The estimation errors of the segmentation method
for different types of noisy signals.
Type of Signal
Segmentation Error
RTS (Fig. 2(b)) 0.014± 0.011
RTS with PCG (Fig. 2(c)) 0.016± 0.010
RTS with WN (Fig. 3(a)) 0.016± 0.013
RTS with WN & PCG (Fig. 3(c)) 0.015± 0.009
RTS with CN (Fig. 4(a)) 0.013± 0.009
RTS with WN & PCG (Fig. 4(c)) 0.018± 0.018
4 CONCLUSIONS
In this paper, effective segmentation of noisy respi-
ratory sound signals is introduced based on genetic
(GA) approach. Using sample entropy, a regular-
ity measure of the time sequence and heterogeneity
measure, the evaluation function of GA is designed.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
126

0 1 2 3 4 5 6 7 8 9
x 10
4
−0.1
−0.05
0
0.05
0.1
0.15
Sample
Segmentation of recorded noisy signal (mild White noise)
0 1 2 3 4 5 6 7 8 9
x 10
4
−0.1
−0.05
0
0.05
0.1
0.15
Segmentation of recorded noisy signal (moderate White noise)
Sample
0 1 2 3 4 5 6 7 8 9
x 10
4
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Segmentation of recorded noisy signal (white noise plus PCG signal)
Sample
(a)
(b)
(c)
Figure 3: Segmentation results of the noisy recorded breath
signal together with (a)-(b) varying white noise;(c) white
noise and PCG.
0 1 2 3 4 5 6 7 8 9
x 10
4
−0.1
−0.05
0
0.05
0.1
0.15
Segmentation of recorded noisy signal (mild colored noise)
Sample
0 1 2 3 4 5 6 7 8 9
x 10
4
−0.1
−0.05
0
0.05
0.1
0.15
Sample
Segmentation of recorded noisy signal (moderate colored noise)
0 1 2 3 4 5 6 7 8 9
x 10
4
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Segmentation of recorded noisy signal (colored noise plus PCG signal)
Sample
(a)
(b)
(c)
Figure 4: Segmentation results of the noisy recorded breath
signal together with (a)-(b) varying colored noise;(c) col-
ored noise and PCG.
The segmentation results for normal tracheal breath
sounds corrupted with heartbeats and ambient noise
are found quite accurate, especially when the existing
methods only perform well on the processed signals
without these noise. The method is found effective in
the presence of various types and levels of noise.
Furthermore, many approaches for initial segment
number estimation (e.g. onset or other detection tech-
niques) are suitable for the proposed segmentation
method. As the performance of the proposed method
does not depend heavily on the accuracy of the total
segment number estimated, only a rough estimation
by using any detection technique is required. More-
over, the independency on threshold values makes the
method very robust and suitable for segmentation of
recorded respiratory sound signals.
REFERENCES
Chipperfield, A., Fleming, P., Pohlheim, H., and Fonseca,
C. (1995). Genetic algorithm toolbox. Department of
Automatic Control and Systems Engineering, Univer-
sity of Sheffield.
Coley, D. A. (2001). An Introduction to Genetic Algorithms
for Scientists and Engineers. World Scientific.
Hult, P., Wranne, B., and Ask, P. (2000). A bioa-
coustic method for timing of the different phases of
the breathing cycle and monitoring of breathing fre-
quency. Medical Eng. and Physics, 22:425–433.
Lehrer, S. (2002). Understanding Lung Sounds. Philadel-
phia, PA: Saunders, Audio CD.
R. L. Wilkins, J. E. H. and Lopez, B. (2004). Fundamentals
of Lung and Heart Sounds. Mosby, Audio CD.
Richman, J. S. and Moorman, J. R. (2000). Physiological
time-series analysis using approximate entropy and
sample entropy. Am J Physiol Heart Circ Physiol,
278(6):H2039–2049.
Rossi, M., Sovijarvi, A. R. A., P. Pirila, L. V., Dalmasso, F.,
and Vanderschoot, J. (2000). Environmental and sub-
ject conditions and breathing manoeuvres for respira-
tory sound recordings. European Respiratory Review,
10(77):611–615.
Tang, K. S., Man, K. F., Kwong, S., and He, Q. (1996).
Genetic algorithms and their applications. Signal Pro-
cessing Magazine, IEEE, 13(6):22–37.
Tilkian, A. G. and Conover, M. B. (2001). Understanding
Heart Sounds and Murmurs: with an Introduction to
Lung Sounds. Philadelphia, PA:Saunders 2001; Audio
CD.
Yadollahi, A. and Moussavi, Z. (2006). A robust method
for estimating respiratory flow using tracheal sounds
entropy. Biomedical Engineering, IEEE Transactions
on, 53(4):662–668.
PHASE SEGMENTATION OF NOISY RESPIRATORY SOUND SIGNALS USING GENETIC APPROACH
127