AUTOMATIC SEGMENTATION OF CAPILLARY NON-PERFUSION

IN RETINAL ANGIOGRAMS

Amit Agarwal, Jayanthi Sivaswamy

CVIT, International Institute of Information Technology, Hyderabad, India

Alka Rani

Aravind Eye Institute, Hyderabad, India

Taraprasad Das

LV Prasad Eye Institute, Hyderabad, India

Keywords:

Capillary Non-Perfusion, Retina, Extrema Pyramid, Disease detection.

Abstract:

Capillary Non-Perfusion (CNP) is a condition in diabetic retinopathy where blood ceases to ﬂow to certain

parts of the retina, potentially leading to blindness. This paper presents a solution for automatically detecting

and segmenting CNP regions from fundus ﬂuorescein angiograms (FFAs). CNPs are modelled as valleys, and

a novel multiresolution technique for trough-based valley detection is presented. The proposed algorithm has

been tested on 40 images and validated against expert-marked ground truth. Obtained results are presented as

a receiver operating characteristic (ROC) curve. The area under this curve is 0.842 and the distance of ROC

from the ideal point (0, 1) is 0.31.

1 INTRODUCTION

Diabetes is occurring in an ever increasing percent-

age in the world. Diabetes mellitus affects many or-

gans of the body, and the eye is one of the organs

that is affected relatively early (compared to the kid-

ney). While diabetes affects all parts of the eye, the

retina (retinopathy) is most commonly affected. Dia-

betic retinopathy progresses in phases. It starts with

microaneurysms and superﬁcial retinal hemorrhages

(non-proliferative diabetic retinopathy; NPDR), pro-

gresses to accumulation of hard exudates in the pos-

terior pole (diabetic maculopathy), and ﬁnally ends

with new vessels in the surface of the retina and/or the

optic disc (proliferative diabetic retinopathy; PDR).

The underlying cause of the terminal event, the reti-

nal new vessels, is retinal ischemia which manifests

as areas of CNP that is most clearly seen in an FFA.

These lesions appear as dark regions in the FFA im-

ages as shown in Fig. 1. If not treated in time, the

CNP areas grow and spread across the entire retina.

Large areas of non-perfusion lead to new vessel for-

mation and bleeding into the vitreous cavity. These

complications are responsible for severe visual loss in

most patients with PDR (Kohner, 1993). FFA guides

the choice and extent of laser treatment in diabetic

maculopathy and PDR.

An automatic identiﬁcation of important events

in FFA is objective and very useful both for referral

and treatment. Automated analyses of FFA images

for the purpose of extracting important structures as

well as lesions have received some attention. Im-

age conditioning solutions that have been proposed

include illumination correction using a parametric

bi-cubic model for the illumination function (Cree

et al., 1999) and noise suppression for a sequence of

angiogram images based on bilateral ﬁltering (Guo

et al., 2005b). In FFA segmentation, stochastic

models have been proposed to segment the fovea,

arteries and veins from the central (macular) view

of FFAs (Sim´o and de Ves, 2001) and among le-

sions, microaneurysms have received much attention.

Several techniques ranging from morphological to

model-based have been proposed for microaneurysm

segmentation (Fleming et al., 2006), (Hafez, 2002)

and (A. M. Mendonc¸a, 1999). An automated tech-

nique for measurement of blood ﬂow in capillaries

has been attempted from angiograms, for determining

the effect of cardio-pulmonary bypass surgery (Jagoe

et al., 1992). The foveal region of the retinal image

170

Agarwal A., Sivaswamy J., Rani A. and Das T. (2008).

AUTOMATIC SEGMENTATION OF CAPILLARY NON-PERFUSION IN RETINAL ANGIOGRAMS.

In Proceedings of the First Inter national Conference on Bio-inspired Systems and Signal Processing, pages 170-177

DOI: 10.5220/0001058201700177

 SciTePress

is processed to enhance the vascular structure and ex-

tract linear segments. The processed results from im-

ages taken before and after the bypass surgeryare then

compared (via a logical AND operation) to identify

the differences. However, to our knowledge, there are

no reports in the literature of any technique to detect

the cause of PDR namely the presence of the CNP re-

gions anywhere in the retina. Detecting and segment-

ing CNPs is the focus of this paper.

The clinical procedure to detect CNPs is a visual

scan of an FFA image. In order to estimate the amount

of area damaged, the scan is generally done on the

composite image of the retina obtained after suitable

mosaicing of several retinal segments. Such a pro-

cedure suffers from several drawbacks: the variable

skills and subjectivity of the observer, which also de-

pend on the quality of the images; a lack of precise un-

derstanding of the area of retina affected which helps

in deciding the nature and extent of laser treatment.

Automated image analysis techniques can be used to

address these issues but there are several challenges in

devising solutions for CNP segmentation. FFAs suf-

fer from non-uniform illumination due to the eye ge-

ometry, imaging conditions and presence of other me-

dia opacity such as cataract. Inter-patient and intra-

patient variablility is also possible. The former is due

to different pupil dilations and the latter is due to the

time of image capture after injection of ﬂuorescein

dye. Another compounding factor is that the mean

grey level of CNPs as well as their shape and size are

variable, with the size ranging from very small to very

large (from 100 to 55000 pixels). Often, the bound-

aries of CNPs are not well deﬁned because of an in-

homogeneous textured background. Thus, the only

visually distinguishing characteristic of a CNP is that

it is relatively darker than its surround.

In this paper, we propose a novel method to ex-

tract and quantify regions of CNP based on modeling

CNPs as valleys in the image surface. The algorithm

for CNP segmentation is developed and its details are

presented in the next section. Section 3 provides im-

plementation details and illustrative test results of the

algorithm. Finally, some discussions and conclusions

are presented in the last section.

2 VALLEY BASED CNP

SEGMENTATION

2.1 Modelling CNP Regions

As discussed earlier, CNP occurs when the capillary

network in a region of the human retina stops func-

tioning and does not supply blood to the correspond-

ing areas. In FFAs, regions receiving normal blood

supply appear as bright white regions since they carry

a ﬂuorescent dye and regions lacking in blood (due

to abnormal supply of blood) appear as dark regions.

Hence, regions of CNP appear as dull/dark lesions

bounded by healthy vasculature.

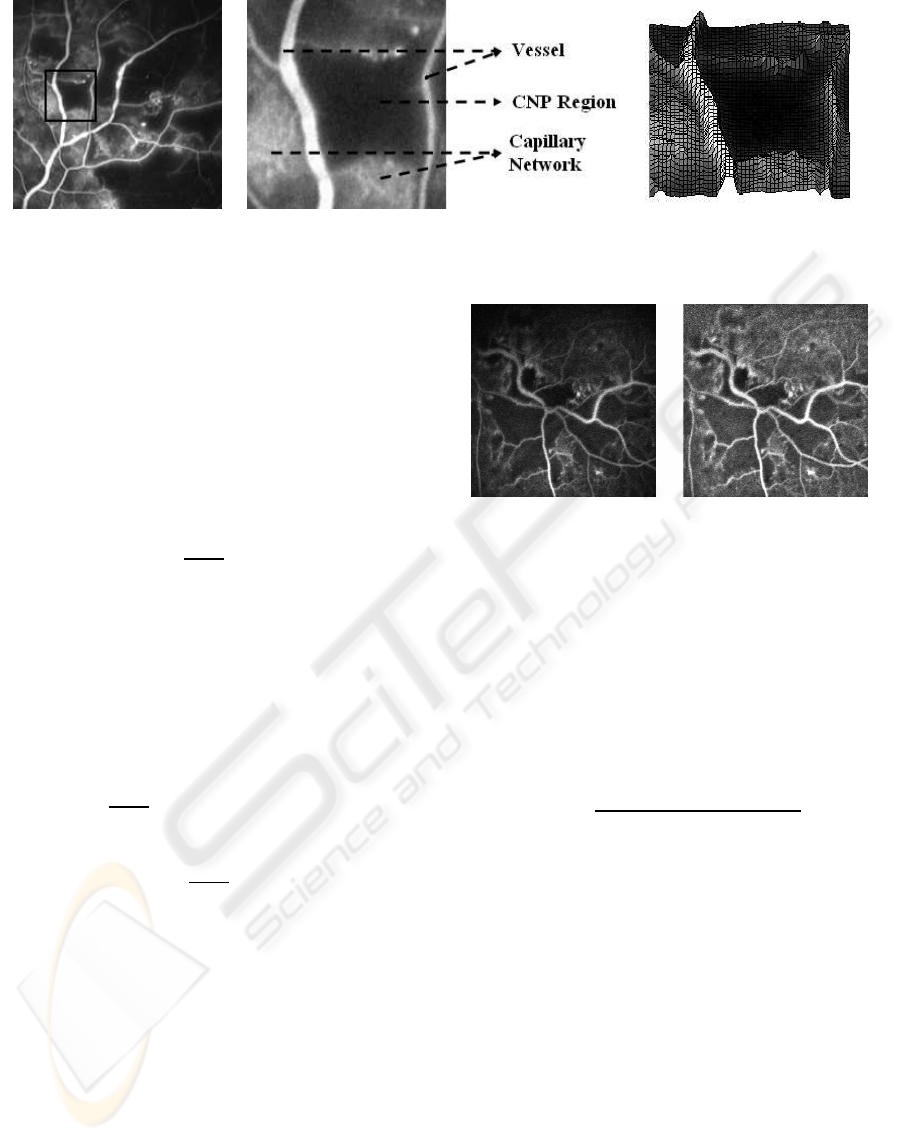
A sample FFA image and an enlarged view of a

CNP region and its surroundings is shown in Fig. 1.

Also, included in this ﬁgure is the surface plot of the

corresponding CNP region from which we can ob-

serve that the prominent vessels, the healthy capillary

network and the CNP have very different topographic

charactersitics: While the major vessel appears as a

ridge, the CNP appears as a valley with the healthy

capillary network appearing as a plateau in the image.

Hence, one can conclude that CNPs can be modelled

as valleys. Watershed-based solution to valley detec-

tion (for example, (Gauch, 1999)) is possible, how-

ever, these result in oversegmentation or in the case

of marker-based versions, require additional informa-

tion. In the case of CNP detection, since the size of a

CNP and the nature of its surround can be highly vari-

able, obtaining such markers can be quite challenging.

A better alternative is to identify the trough (lowest

point on a curve) and use it to segment a CNP. Hence,

we have taken a different approach to the problem

and propose a technique that detects trough points and

collates them across scales. We next present the de-

tails of our proposed algorithm for CNP segmentation

comprising several steps.

2.2 CNP Detection Algorithm

The proposed CNP detection algorithm consists of

these stages: Firstly, illumination correction (IC) is

done to minimise the background intensity variation

followed by denoising to eliminate noise that is fre-

quently found in FFAs. Next, valley detection is per-

formed to locate the seed points in the CNP regions

which are used to extract the candidate CNP regions

using a region growing algorithm. Finally, threshold-

ing is done to reject false positives among the detected

candidates. The processing in each of these stages are

described next.

2.2.1 Illumination Correction

Nonuniform illumination is a problem in retinal

colour images as well as angiograms. A camera-

model based solution for illumination correction in

angiograms, obtained with non-confocal imaging, is

given in (Cree et al., 1999) which assumes a macula-

centric view of the retina. Our images are not neces-

sarily macula-centric and are obtained from a laser-

AUTOMATIC SEGMENTATION OF CAPILLARY NON-PERFUSION IN RETINAL ANGIOGRAMS

171

(a) (b) (c)

Figure 1: (a) A sample FFA image with CNP. (b) Enlarged view and (c) surface plot of the CNP region in (a).

based confocal imaging system. We modiﬁed a quo-

tient based approach proposed for face images (Wang

et al., 2004) and model the non-uniform illumination

as a multiplicative degradation function which is es-

timated by blurring the corrupted image. Let I(x, y),

(x, y) and I

(x, y) denote the given, smoothed and

corrected images, respectively and l

be the desired

level of illumination. The corrected intensity value at

location (x, y) is found as

(x, y) =

(

I(x, y) ×

(x,y)

if I

(x, y) < l

I(x, y) if I

(x, y) ≥ l

(1)

As can be observed from Eq. 1, a pixel where the

estimated illumination is greater than the ideal illumi-

nation value is not corrected. This is to ensure that

the regions which are inherently bright, like the optic-

disk, haemorrhages, etc., are not wrongly classiﬁed

as regions of excessive illumination and corrected ac-

cordingly. When the estimated illumination value is

less than the ideal illumination value, multiplication

by the fraction

(x,y)

ensures that regions with illumi-

nation less than the l

are elevated to the ideal illu-

mination value. Moreover, contrast at such a pixel is

improved by a factor of

(x,y)

thereby removing the

need for subsequent brightness and contrast opera-

tions, as required in the case of quotient-image based

technique. A sample FFA image and corresponding

illumination corrected image is shown in Fig. 2.

2.2.2 Noise Removal

The laser-based imaging produces ﬁne-grain speckle

type of noise in the angiograms as can be seen in

Fig. 2. A bilateral ﬁlter-based approach proposed

for color and gray scale images in (Tomasi and Man-

duchi, 1998) has been successfully applied to denoise

images in an angiogram sequence (Guo et al., 2005a).

The strength of bilateral ﬁlter based denoising is its

ability to denoise without compromising edge qual-

ity. This is due to the ﬁlter’s nonlinear characteristic

Figure 2: A sample FFA image and Illumination corrected

image.

which permits one to take into account the spatial dis-

tance as well the photometric similarity of a pixel to

its neighbors. The spatial context is provided by a

domain ﬁlter while the photometric similarity is con-

trolled by a range ﬁlter. We use a version of the bilater

ﬁlter for our noise removal task which is described

next. Given an input pixel I(P), the output pixel I

(P)

is found as

(P) =

∑

I(Q)W

(P, Q)W

(P, Q)

∑

(P, Q)W

(P, Q)

(2)

where P and Q are position vectors, w is the current

neighbourhood and W

, W

are Gaussian kernels of

the domain and range ﬁlters respectively. The edge

preservation feature of the bilateral ﬁlter can be seen

in the results of preprocessing (illumination correc-

tion + denoising) in Fig.6 (b).

2.2.3 CNP Segmentation

Now we turn to the main task of detecting and seg-

menting CNP regions. Since we have modelled CNPs

as valleys, a valley detection algorithm is needed to

detect seed points in the CNP regions. As the CNPs

vary widely in size, the valleys can be extended.

Hence, a multiresolution approach is appropriate. The

strategy we have adopted is to reduce the valleys to

a single trough point via a pyramidal decomposition

and then detect them using a trough detector at each

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

172

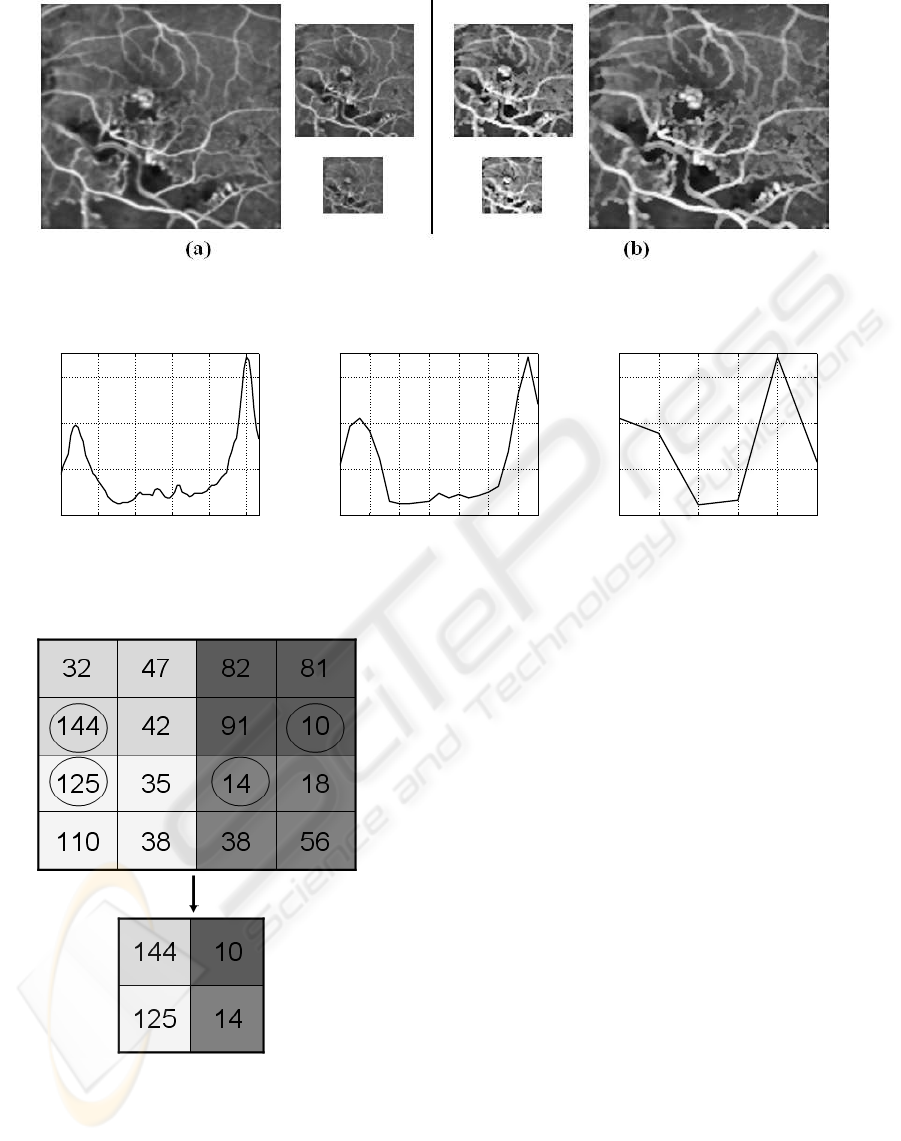
Figure 3: An FFA image at levels 3, 4, 5 in the (a) conventional and (b) proposed pyramidal decomposition.

0 15 30 45 60 75 80

100

140

180

200

Pixel Number

Intensity

0 3 6 9 12 15 18 20

100

140

180

200

Pixel Number

Intensity

0 1 2 3 4 5

100

140

180

200

Pixel Number

Intensity

(a) (b) (c)

Figure 4: Intensity proﬁle of a CNP and its surround, at levels (a) 1, (b) 3 and (c) 5 of the image pyramid.

Figure 5: Example demonstrating Equation 3.

level and collating them. Each of these steps are de-

scribed next.

Extrema pyramid decomposition - A conventional

pyramidal decomposition based on averaging and

subsampling is inadequate for the problem at hand.

This can be illustrated with an example shown in Fig.

3. It can be seen that the averaging process dulls the

entire image and will therefore adversely affect CNP

detection based on troughs. Another drawback with

the averaging process is the difﬁculty in localising of

the trough points in the full resolution image when

performing the upsampling process after trough de-

tection. In the problem at hand, the CNP regions are

generally bigger and darker relative to the brighter re-

gions which are thin. Averaging and down-sampling

will result in the bright regions to disappear faster

than the CNP regions, whereas for locating troughs,

it would help to more or less retain the bright regions

across several levels while accepting some loss in the

CNP area. Hence, to preserve the relation between

a CNP and its surround, and maintain the depth of

the valley across levels, we need a method for pyra-

midal decomposition that will minimise the CNP re-

gions at a much faster rate compared to the brighter

surrounding regions. This calls for a controlled multi-

resolution technique. One option is to generate a

pyramid by retaining intensity maxima which will en-

sure the thinner bright regions are largely preserved

during downsampling. However, this is detrimental

to the relative contrast between a CNP and its sur-

round as it elevates the average intensity of the CNP

regions. The end result is a lowering of the depth of

AUTOMATIC SEGMENTATION OF CAPILLARY NON-PERFUSION IN RETINAL ANGIOGRAMS

173

the troughs, which is undesiarbale. A better alterna-

tive is to generate the pyramid through an adaptive

selection of pixels. The solution we propose is a tech-

nique for decomposition which is based on intensity

extrema. Speciﬁcally, given an image I

of size M× N

a L-level decomposition is found as follows:

(m, n) =



min{g

i, j

(m, n)} if g

i, j

(m, n) ≤ t

max{g

i, j

(m, n)} otherwise .



(3)

∀ i, j = 0, 1

where g

i, j

(m, n) = I

l−1

(2m+ i, 2n+ j), with l = 2, ...L

and t is a suitable threshold, taken to be the global

mean in our experiments. An illustration of the equa-

tion is given in Fig. 5 for t = 100.

In an extrema pyramidal decomposition of an an-

giogram, the CNP regions diminish in size at a much

faster rate than non-CNP regions across the levels.

This is illustrated in Fig. 3 (b) where the thickness of

vessels are more or less preserved but the CNPs are

reduced to near-dots in the lowest level image. This

effect is also seen from the intensity proﬁles shown

in Fig. 4, along a horizontal line passing through a

CNP region at different levels. The width of the val-

ley reduces from 50 pixels at the ﬁrst level, to about

1 pixel in the ﬁfth level whereas the image has been

downsampled by 16 between these levels. The rel-

ative brightness value (130) of the ridge and valley

regions is preserved as a result of not performing a

smoothing operation.

Trough detection - A trough is deﬁned as the low-

est point on a curve. Alternatively, the brightness at a

trough is a local minimum. Since the context in which

CNPs, and hence troughs, occur is variable in an an-

giogram, two parameters can be used to characterise

a trough: µ, the mean brightness of the surround and

P, the peak factor which represents the depth of the

trough. These two parameters are used to develop the

following trough detection algorithm in which the im-

age is denoted by I(x, y).

For every pixel (x,y) do the following:

1. Initialize a Boolean variable isTrough = False.

2. Check if I(x,y) is a local minimum in a M × M

neighborhood.

3. If yes, then calculate the mean (µ) of a N × N

neighborhood, with N > M. Else, do nothing.

4. Let T = µ*P and check if I(x, y) < T.

5. If yes, then isTrough = True.

6. If isTrough = True, then mark I(x,y) as a trough

pixel. Else, do nothing.

The threshold T represents the depth of the val-

ley from the mean µ. Since the image pyramid re-

tains extrema, this threshold value has to be carefully

chosen to ensure that enough seed pixels are captured

in a valley while minimising the possibility of false

alarms. A region with low µ is likely to be a CNP

region and hence the required depth for that region

is less whereas the same may not be true if µ is high

and hence, a stricter condition is required in the latter

case. Thus, choosing T proportional to µ is appro-

priate. Furthermore, since trough detection is carried

out at multiple levels a peak factor has to be chosen

for each level. A guiding factor in this choice is that

due to retention of extremas, the likelihood of the lo-

cal minima being a CNP region will be higher at upper

levels. Hence, the peak factor should be progressively

increased with the levels in the pyramid.

After performing trough detection at all levels, the

results are combined with a simple logical OR oper-

ation. For locating the seed pixels in the original im-

age, the fact that the extrema of four pixels is selected

at every level is used iteratively.

CNP region extraction - The detected trough

points can serve as seed points for region based ap-

proach to segmenting the CNP regions. Although

geometric methods can potentially yield better re-

sults, as an initial experiment we chose to use a sim-

ple region growing technique for extracting the CNP

regions as it was computationally simpler. Given

the variability of the appearance of the CNP re-

gions within and across images, the traditionally

used intensity-based homogeneity criterion for region

growing is not suitable. Instead, by noting that CNP

regions are smooth, the better alternativeis to perform

the pixel aggregation in the variance space.

In our experiments, the range for the variance was

taken to be ±4. In order to reject false candidates, a

ﬁnal thresholding operation was performed. A thresh-

old based on the global mean intensity was applied

since the global mean is always lowered with the pres-

ence of CNPs.

3 IMPLEMENTATION AND

RESULTS

The proposed algorithm was implemented as follows.

In the illumination correction stage, the ideal illumi-

nation l

in (1) was set to be roughly half the maxi-

mum grey value in the image or 120. The smoothed

image was obtained with a 30 × 30 Gaussian mask

on a subsampled (by 4) version of the original image

for faster processing. The resulting image was up-

sampled, one level at a time, while blurring the image

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

174

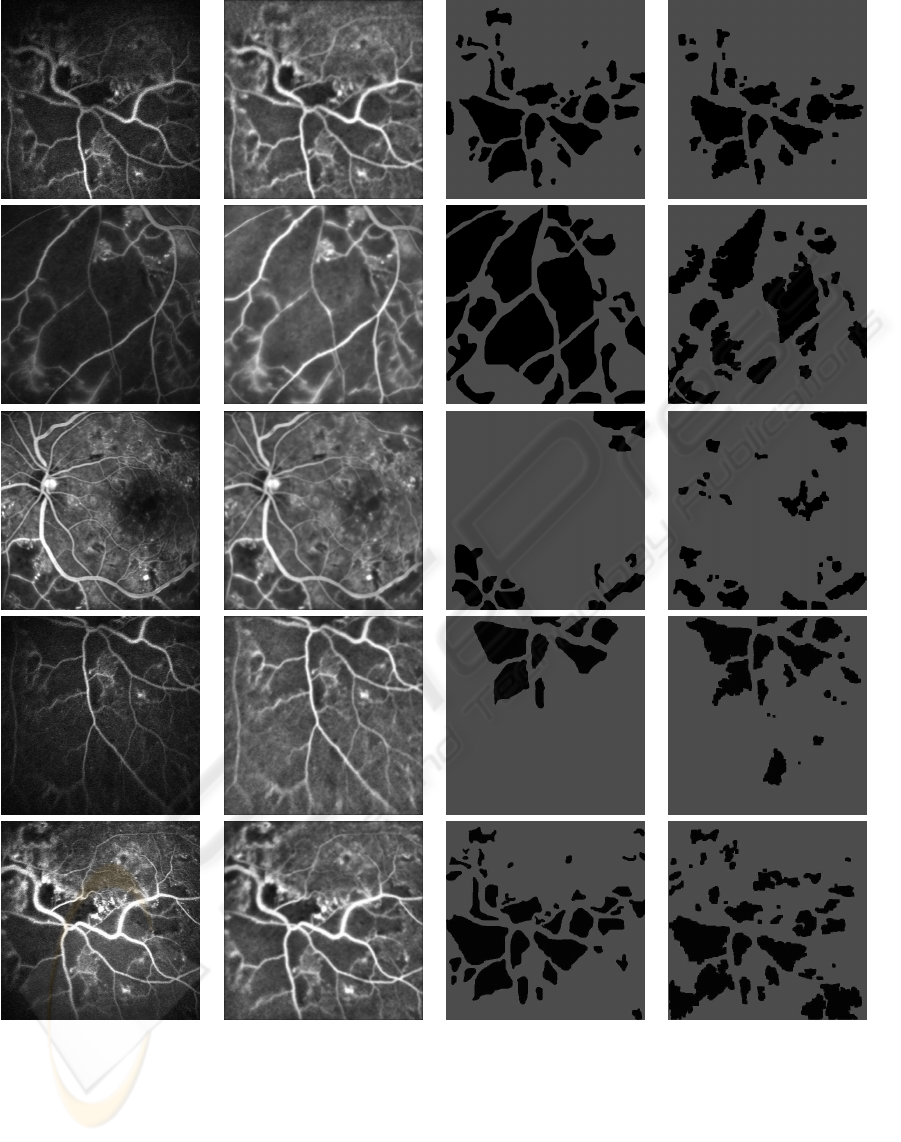
(a) (b) (c) (d)

Figure 6: Results: (a) Sample images, (b) preprocessed image, (c) corresponding ground truths and (c) segmented results with

CNP regions shown in black.

using a 5× 5 Gaussian mask at each upsampled level.

For denoising, a ﬁlter kernel size of 9 × 9 was used

and σ for the domain and range ﬁlters were ﬁxed at

3 and 10 respectively. For valley detection, a 5-level

pyramid was generated; M, N were ﬁxed at 5 and 7

respectively and the peak factor was incremented by

0.02 at each level in the pyramid. In region growing,

the variance was calculated over a 5 × 5 neighbour-

hood.

The proposed CNP segmentation algorithm was

AUTOMATIC SEGMENTATION OF CAPILLARY NON-PERFUSION IN RETINAL ANGIOGRAMS

175

tested on 40 images which contained many CNPs.

These were acquired from the digital confocal scan-

ning laser ophthalmoscope of Heidelberg Retina An-

giograph. The images were of retinal segments for

which the ground truth, in the form of boundaries of

CNPs, were prepared manually by a retina expert (a

co-author). Some sample test images along with cor-

responding ground truth and results of our CNP seg-

mentation algorithm, with a peak factor of 0.41, are

shown in Fig. 6 (a), (b) and (c) respectively. CNP

regions are shown in black in both ground truth and

segmented results. The ﬁve sample test images indi-

cate the variability in images in terms of quality, size

of CNPs and presence of other structures such as op-

tic disk, macula and microaneurysms. A quantitative

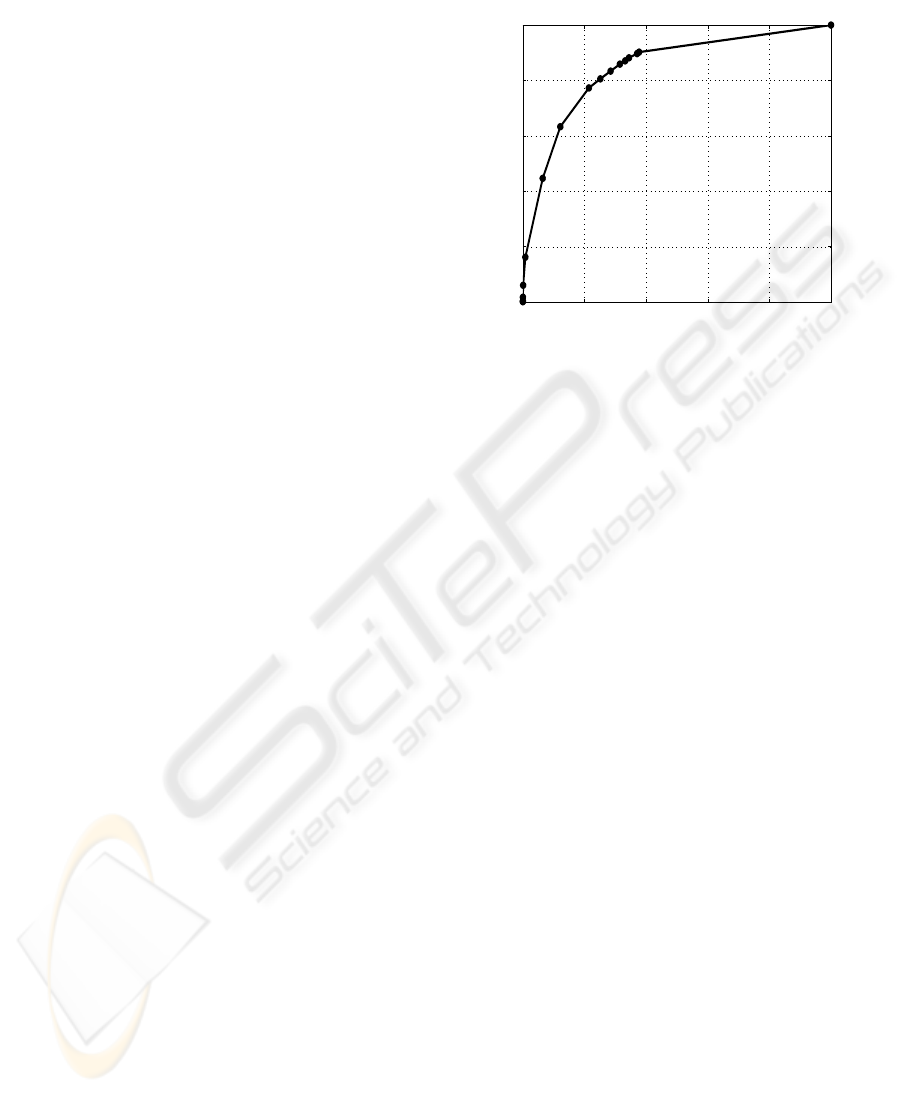
assessment of the algorithm was done using a ROC

curve and not a FROC curve since the area of CNP

is of clinical interest. A comparison between com-

puted and marked CNP segments was done on a pixel

by pixel basis. By using the peak factor as a control

parameter, the obtained ROC curve, shown in Fig. 7,

was found to have an area under the curve (AUC) of

0.842 and a distance (D

) to the ideal point (1,0) of

0.35. The ideal values for AUC and D

are 1 and 0

respectively.

4 CONCLUDING REMARKS

An unsupervised algorithm for automatically seg-

menting CNPs from FFA images has been presented.

Its overall performance is quite good as indicated by

the ROC curve and the AUC, D

metrics. Since there

is no reported work on this problem it is not possible

to do any benchmarking. A visual inspection of seg-

mented results indicates that the algorithm success-

fully detects CNPs of all sizes, however, it tends to

undersegment large CNPs because the IC stage inten-

siﬁes the variability within CNPs. A failure analysis

indicates that the macula region gets mislabled as a

CNP (as seen in the bottom row of Fig. 6) since the

two have similar characteristics, and CNPs in the im-

age peripherytend to be missed since the valley model

is weak in this region.

The main focus of the presented work was on de-

tection of CNPs. Hence, while the performance our

current implementation is quite good, there is scope

for improvement of the algorithm’s performance: ge-

ometric techniques such as fast marching method in

(Malladi and Sethian, 2006) can be used to more

accurately extract the CNP region boundaries while

a pixel-based classiﬁer will help improve the rejec-

tion of the false alarms. Likewise, incorporation of a

macula detection stage will help the algorithm from

falsely classifying macula as a CNP region.

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

False Positive Fraction

True Poitive Fraction

Figure 7: ROC plot.

Finally, it should be noted that the ground truth

generation process for CNPs is a laborious one.

Retina experts found it challenging to draw precise

boundaries because they often appear to be intricate

or ill-deﬁned. This points to the need for the use of

multiple expert-markings for a fuller evaluation of the

algorithm. Such an exercise might also shed light on

the degree of observer bias in CNP segmentation.

REFERENCES

A. M. Mendonc¸a, A. J. Campilho, J. M. N. (1999). Auto-

matic segmentation of microaneurysms in retinal an-

giograms of diabetic patients. In Proc. International

Conf. on Image Analysis and Processing, pages 728 –

733.

Cree, M. J., Olson, J. A., C.McHardy, K., Sharp, P. F., and

Forresters, J. V. (1999). The preprocessing of retinal

images for the detection of ﬂuorescein leakage. Phys.

Med. Biol., 44:293 – 308.

Fleming, A. D., Philip, S., Goatman, K. A., Olson, J. A.,

and Sharp, P. F. (2006). Automated microaneurysm

detection using local contrast normalization and local

vessel detection. In IEEE Trans. on Medical Imaging,

volume 25, pages 1223 – 1232.

Gauch, J. M. (1999). Image segmentation and analysis via

multiscale gradient watershed hierarchies. In IEEE

Trans. on Image Processing, volume 8, pages 69 – 79.

Guo, X.-X., Lu, Y.-N., Xu, Z.-W., Liu, Z.-H., Wang, Y.-X.,

and Pang, Y.-J. (2005a). Noise suppression of ﬂuo-

rescein angiogram sequences using bilateral ﬁlter. In

Proc. International Conf. on Machine Learning and

Cybernetics, volume 9, pages 5366 – 5371.

Guo, X.-X., Lu, Y.-N., Xu, Z.-W., and Pang, Y.-J. (2005b).

An eawa ﬁlter for denoising of ﬁltering of ﬂuorescein

angiogram sequences. In Proc. International Conf. on

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

176

Computer and Information Technology, pages 614 –

618.

Hafez, M. (2002). Using adaptive edge technique for detect-

ing microaneurysms in ﬂuorescein angiograms of the

ocular fundus. Proc. Mediterranean Electrotechnical

Conf., pages 479 – 483.

Jagoe, R., Arnold, J., Blauth, C., Smith, P., K.M.Taylor,

and Wootton, R. (1992). Measurement of capillary

dropout in retinal angiograms by computerised image

analysis. Pattern Recognition Letters, 13:143 – 151.

Kohner, E. M. (1993). Diabetic retinopathy. BMJ,

307(6913):1195 – 1199.

Malladi, R. and Sethian, J. A. (2006). Fast methods for

shape extraction in medical and biomedical imaging.

In R Malladi (ed) Geometric Methods in Bio-medical

Image Processing. Berlin, Springer, pages 49–61.

Sim´o, A. and de Ves, E. (2001). Segmentation of macular

ﬂuorescein angiographies. a statistical approach. Pat-

tern Recognition, 34:795 – 809.

Tomasi, C. and Manduchi, R. (1998). Bilateral ﬁltering for

gray and color images. In Proc. International Conf.

on Computer Vision, pages 839–846.

Wang, H., Li, S. Z., and Wang, Y. (2004). Generalized quo-

tient image. In Proc. Conf. on Computer Vision and

Pattern Recognition, volume 2, pages 498 – 505.

AUTOMATIC SEGMENTATION OF CAPILLARY NON-PERFUSION IN RETINAL ANGIOGRAMS

177