REGISTRATION AND RETRIEVAL OF ELONGATED

STRUCTURES IN MEDICAL IMAGES

Alexei Manso Correa Machado and Christiano Augusto Caldas Teixeira

Pontiﬁcal Catholic University of Minas Gerais, Av. Dom Jose Gaspar, 500, Belo Horizonte, MG, Brazil

Keywords:

Medical imaging, morphology, image registration, information retrieval.

Abstract:

This work aims at proposing a set of methods to describe, register and retrieve images of elongated struc-

tures from a database based on their shape content. We propose a registration algorithm that jointly takes

into account the gross shape of the structure and the shape of its boundary, resulting in anatomically consis-

tent deformations. The method determines a medial axis that represents the full extent of the structure with

no branches. Registration follows the linear elasticity model and is implemented through dynamic program-

ming. Discriminative anatomic features are computed from the results of registration and used as variables in a

content-based image retrieval system. A case study on the morphology of the corpus callosum in the chromo-

some 22q11.2 deletion syndrome illustrates the effectiveness of the method and corroborates the hypothesis

that retrieval systems may also act as knowledge discovery tools.

1 INTRODUCTION

Elongated structures such as vessels, bones and brain

ventricles are of interest in many problems and ap-

plications (Toledo et al., 2000; Staal, 2004). Those

structures have in common the fact that their gross

shape can be efﬁciently represented by centerlines or

medial axes. Contour may present important anatom-

ical features, but the overall shape is, if not more, as

important as the shape of the boundary.

This work aims at proposing a set of methods to

describe, register and ultimately retrieve images of

elongated structures from a database based on their

shape content. Image registration techniques have

been widely used in morphometry, as it provides de-

tailed description of the anatomy, taking a reference

image as a basis for comparison. Registration algo-

rithms are nevertheless computationally costly and,

when applied to the whole image or to the boundary

of elongated structures, may yield unsatisfactory re-

sults. A contribution of this work is a registration al-

gorithm that takes into account both the gross shape

of the structure and the shape of its boundary, with

emphasis to the former aspect.

Figure 1 shows a schematic of a content-based

image retrieval (CBIR) system that follows this ap-

proach. A set of images depicting elongated struc-

tures is segmented and the structures represented by

their boundaries and medial axes. Another image,

taken as a common reference, is deformed through

elastic registration so as to align its anatomy with the

anatomy of the images in the dataset. The result of

registration is a mapping function from each point in

the reference to a point in the target image that en-

able detailed shape description. After the structures

have been described, e.g. based on the curvature of

their boundaries and medial axes, they are stored in

the database for future searching. The querying phase

follows the same steps used to convert the images into

descriptive features. The query image converted to

the corresponding feature vector is compared with the

database, the most similar images are retrieved and

presented to the user. The user may rank the results

according to their relevance, choose one of the re-

trieved images as a new query or redeﬁne a region

of interest that should be given greater priority in the

next retrieving iteration. The query vector is therefore

updated taking into account the user’s feedback.

The characterization of the gross shape is criti-

cal to the registration and retrieval of elongated struc-

tures. We also present a semi-automatic solution to

the extraction of a medial axis that represents the full

extent of the structure with no branches. Finally, dis-

criminative anatomic features are computed from the

results of registration and used as variables in a CBIR

system. A case study on the morphology of the corpus

146

Manso Correa Machado A. and Augusto Caldas Teixeira C. (2008).

REGISTRATION AND RETRIEVAL OF ELONGATED STRUCTURES IN MEDICAL IMAGES.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 146-153

DOI: 10.5220/0001058901460153

 SciTePress

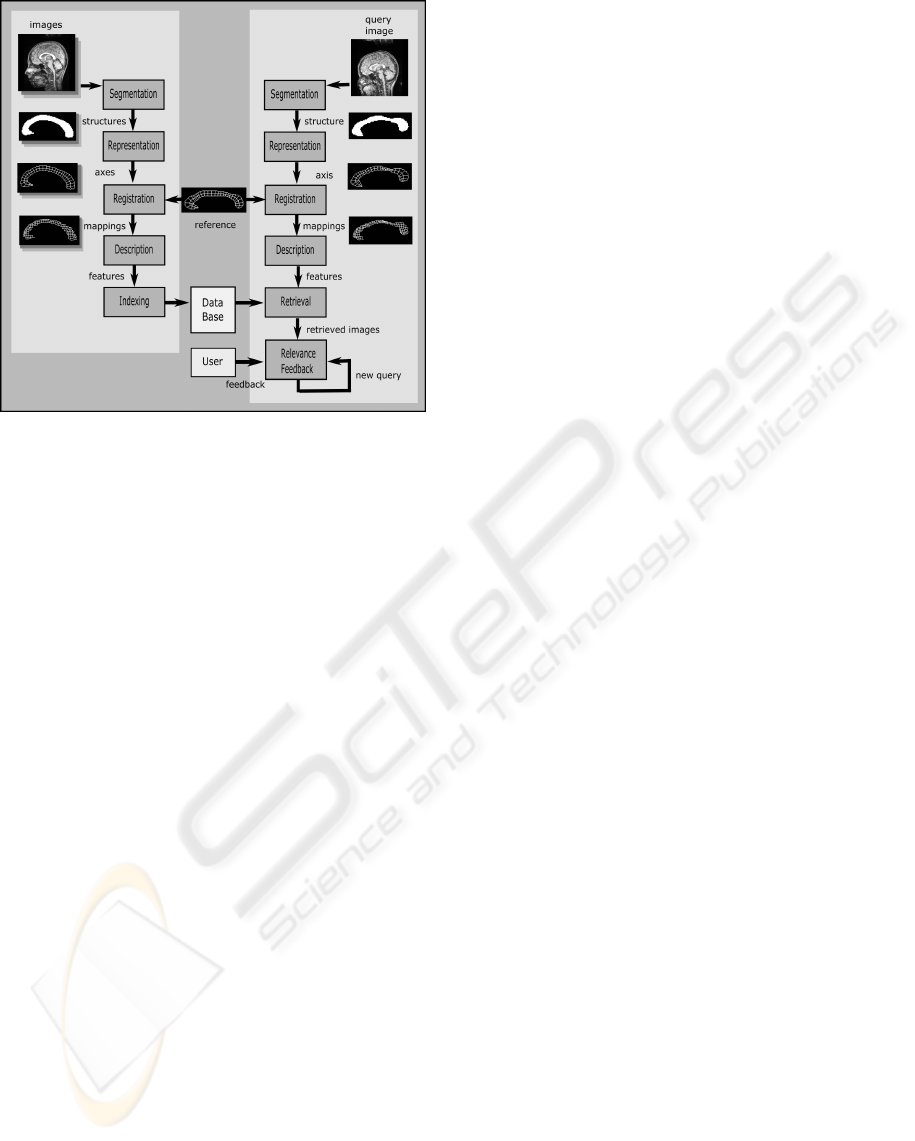
Figure 1: Schematic of a CBIR system based on registra-

tion. The left part of the scheme shows the steps performed

off-line for each image in the database. The on-line part of

the retrieval process is shown in the right. The link between

the on-line and off-line phases is the reference image that

is registered to the query and to the database, establishing a

basis for shape comparison.

callosum in the chromosome 22q11.2 deletion syn-

drome illustrates the effectiveness of the method and

corroborates the hypothesis that CBIR systems may

also act as knowledge discovery tools.

2 RELATED WORKS

The representation of elongated structures through

single sequences of connected points that describe

their intrinsic geometry has been extensively stud-

ied. Pioneered by Blum and Nagel (Blum and Nagel,

1978), the use of medial axes to describe 2D shapes

is based on the removal of points in the boundary un-

til the gross shape is minimally represented. Many

skeleton and thinning algorithms can be found in the

literature, revealing the difﬁculty on determining a

standard deﬁnition for medial axis (Dvies and Plum-

mer, 1981). Other more complex models include the

medial representations (Pizer et al., 2003; Yushkevich

et al., 2003), in which the medial axis and a radial

scalar ﬁeld are parametrically described such that the

boundary can be further reconstructed, and the medial

proﬁles (Hamarneh et al., 2004), that provide a shape

representation and deformation operators that can be

used to derive shape distributions.

Registration is considered one of the most im-

portant approaches to provide detailed description of

shape. Automatic registration algorithms (McInerney

and Terzopoulos, 1996; Toga, 1999) may be applied

to the contour (Cootes et al., 1994; Davatzikos and

Prince, 1995) or medial axis (Pizer et al., 1996; Gol-

land et al., 1999) of speciﬁc structures. Registration is

also used together with the medial axis transform (Xie

and Heng, 2005) to align the anatomy of structures

based on their skeletons.

Retrieval of images based on their content is still

in its infancy. Smeulders (Smeulders et al., 2000) and

Lew (Lew et al., 2006) present comprehensive dis-

cussions on the main aspects and challenges of im-

age retrieval. Muller (Muller et al., 2004) shows how

CBIR systems can be used to retrieve images in gen-

eral medical databases. In the next section, we dis-

cuss the speciﬁc issues related to the registration and

retrieval of images depicting elongated structures and

propose a registration algorithm that jointly considers

the axis and boundaries of such structures.

3 METHODS

The proposed image retrieval method can be divided

into four steps: midline extraction, registration, de-

scription and retrieval.

3.1 Midline Extraction

A midline can be deﬁned as a curve that splits the

structure into dorsal and ventral regions, such that,

at any point, the perpendicular line segments con-

necting the midline to dorsal and ventral parts of the

boundary have roughly the same length (properties

of perpendicularity and congruency). Midline extrac-

tion starts by determining a skeleton based on a vari-

ation of the thinning algorithm described by Gonza-

lez and Woods (Gonzalez and Woods, 2002), for 8-

connected objects. Object points are labeled as 1 and

the background is set to 0. In order for the curve to

fully extend from one extremity to the other, two ob-

ject points are manually chosen and forced to be re-

spectively the starting and ending points of the skele-

ton.Additionally, the thinning algorithm is modiﬁed

so as to prune any other branches of the structure’s

skeleton. The ﬁnal curve is, therefore, a single se-

quence of pixels, each one connected to two neigh-

bors, with the exception of the starting and ending

points.

The following algorithm summarizes skeleton ex-

traction, where p

and p

are the endpoints; the neigh-

bors of p are denoted as n

, numbered counterclock-

wise from 0 (east) to 7 (southeast); function N re-

turns the number of neighbors of p that belong to the

object, i.e., N(p) =

∑

; and function S returns the

REGISTRATION AND RETRIEVAL OF ELONGATED STRUCTURES IN MEDICAL IMAGES

147

number of connected sequences of object points in

the neighborhood of p, i.e., read as an 8-bit string,

the neighbors of p must match the regular expres-

sion 0

∗

. It can be shown that only 42

neighborhood conﬁgurations satisfy the condition to

mark a point, so that the algorithm can be efﬁciently

implemented using look-up tables:

Repeat

For each point p of the object, p /∈ {p

, p

}, do

If N(p) < 7 and S(p) = 1 and n

+ n

) = 0

Mark p to be removed;

Remove marked points;

For each point p of the object, p /∈ {p

, p

}, do

If N(p) < 7 and S(p) = 1 and n

+ n

) = 0

Mark p to be removed;

Remove marked points;

until no more points can be removed.

The linear length of the skeleton is computed con-

sidering the distances between each pair of consecu-

tive pixels: pixels connected by a face with distance

equals to 1 and the ones connected by a vertex with

distance equals to

√

2. The coordinates of the pix-

els are smoothed and interpolated so as to yield an

isotropic rotation-invariant representation of the mid-

line. The derivative of this curve, taken at equidis-

tant points, guides the computation of perpendicu-

lar segments that link the dorsal and ventral bound-

aries of the structure. Problems may occur in regions

where the midline presents increased curvature. In

this case, it may be impossible to satisfy the require-

ments of perpendicularity and congruency for the seg-

ments. Figure 2 shows an example where two con-

secutive segments intersect each other as the result of

increased midline curvature. A solution for this prob-

lem is to violate the property of perpendicularity so

that points with increasing coordinates at the midline

will be connected to points of non-decreasing coordi-

nates at both boundaries. It is however expected that

elongated structures will not frequently incur in this

problem.

The curvature (second derivative) of the midline

can be determined based on the k-curvature metric,

that is deﬁned in each point p

= (x

) as the differ-

ence between the average of the derivatives at the k

next points and the average of the derivatives at the k

previous points (including p

kcurv(p

) =

(

i+k

∑

j=i+1

d(p

) −

∑

j=i−k+1

d(p

)), (1)

d(p

) = tan

−1

−x

j−1

−y

j−1

Parameter k should be empirically chosen so as to pro-

vide enough smoothness. The midline curve should

be extrapolated at the extremities (e.g. based on au-

toregression), so that the curvatures will be computed

over all the midline extension. Analogously, the cur-

vature at the dorsal and ventral boundaries should be

computed at the intersection of the segments. The cur-

vatures at the midline and boundaries will play a fun-

damental role as a measure of similarity during regis-

tration.

Figure 2: Example where consecutive segments intersect

each other as the result of increased midline curvature (a)

and the solution to the problem (b).

3.2 Image Registration

The images in the database should be registered to

a reference in order to establish a common basis

for comparison. Image registration can be stated as

the process of determining a correspondence between

each point p in the midline of the reference image

to a point u(p) in the midline of the subject image.

Let C

(p) = kcurv(p) − kcurv(u(p)) be the differ-

ence between the k-curvature taken at point p in the

reference midline and the k-curvature taken at point

u(p) in the subject midline. Analogously, let C

and

be the same difference function computed respec-

tively at the intersection points of the perpendicular

segments emanating from the midline with the dorsal

and ventral boundaries.

The cost function to be minimized is given as

cost = D −S, (2)

where D is the deformation penalty and S is the sim-

ilarity between the curvatures of registered points of

the midline, dorsal and ventral boundaries, given as

D = α

(

du(p)

d p

)

d p + β

(

u(p)

d p

)

d p,

S =

∑

i∈{M,D,V }

(p)

d p (3)

Parameters α and β weight the amount and

smoothness of deformation, respectively. Parameters

, γ

and γ

are negative and weight the importance

of the similarity terms computed respectively for the

midline, dorsal and ventral boundaries.

Registration is performed through dynamic pro-

gramming, in which equidistant points in the refer-

ence midline are mapped to points in the midlines

of the database by minimizing the cost function in

(2). After registering the midlines and corresponding

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

148

boundaries, thin plate splines (Barrodale et al., 1993)

are used to interpolate the warping applied to these

curves to the whole structure, so that each pixel in the

reference image is assigned a displacement vector.

An advantage of the proposed registration algo-

rithm is that it will always map a segment perpendic-

ular to the reference midline to a segment perpendic-

ular to the midline of the subject image. This is a

very important constraint to be observed when deal-

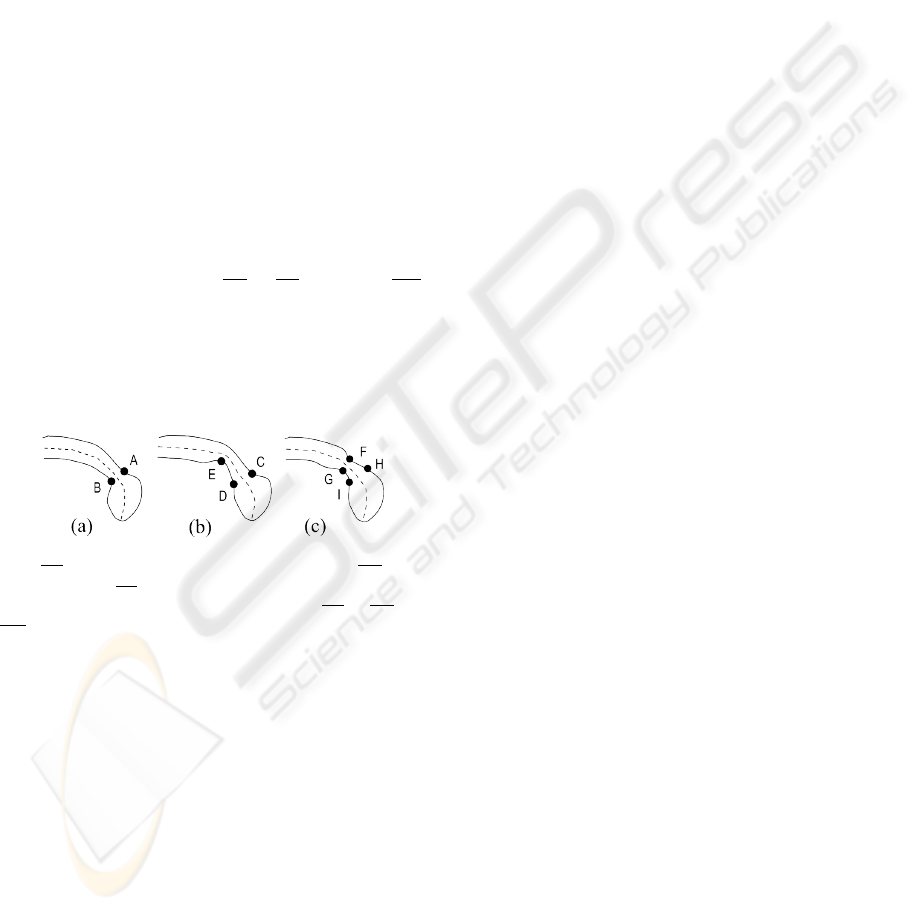
ing with elongated structures. Fig 3 shows two ex-

amples where an image registration algorithm based

only on the boundary or only on the midline would

fail to provide satisfactory deformations. The struc-

ture in (a) is the reference, whose boundary points

A and B must be found correspondence in the other

structures. A registration algorithm that takes into ac-

count only the boundaries would map point A to C

(correctly), but B to E instead of D, since the bound-

ary curvature in B is more similar to the curvature in

E than it is in D. If, on the other hand, the algorithm

is based only on the curvature of the midline, the reg-

istration of the reference to the structure in (c) would

probably map the segment AB to HI instead of FG,

ignoring the similarity between the curvatures at the

boundaries. The similarity function proposed in (3)

avoid both mistakes, since the curvatures at the mid-

line, dorsal and ventral boundaries are jointly taken

into account.

Figure 3: Examples of unsatisfactory registration of the seg-

ment AB in the reference structure (a) to segment CE in (b)

and to segment HI in (c). An algorithm based on both the

boundary and midline would correctly map AB to CD and

FG.

Evaluating the effectiveness of registration meth-

ods is always a difﬁcult task, as ground truth data

is usually inexistent, particularly when the structure

being registered does not present well-deﬁned land-

marks. Alternatively, landmarks may be chosen by

experts, but in this case human subjectivity and lack

of repeatability should be considered in the analysis.

In this work, we designed an interactive interface in

which an expert chooses a set of landmarks in the ref-

erence structure and the corresponding loci in the sub-

jects. The procedure is repeated after 2 weeks, in or-

der to evaluate repeatability. The results achieved by

automatic registration are compared to the mapping

provided by the expert: if the result falls within the

interval of values provided by the expert, it is consid-

ered satisfactory, otherwise the distance in millime-

ters to nearest value is stored and averaged.

3.3 Description

The output of registration is a displacement ﬁeld that

maps each pixel of the reference image to a point in

the subject. From this set of vectors, it is possible

to obtain diverse measurements that describe the im-

aged objects, such as point-wise area and length varia-

tion, curvature of axes and contours, relationships be-

tween axes of orientation, moments and other shape

descriptors. Feature selection is a fundamental step

in image retrieval systems, as it determines the effec-

tiveness and efﬁciency of many algorithms. The set

of features that will represent the objects should be

concise and discriminative, as distinguishing features

facilitates the retrieval of relevant images, while non-

relevant characteristics are confounders. Feature se-

lection and information retrieval are synergetic steps:

while the choice of distinguishing features increases

the relevance of retrieval results, retrieval itself act as

a ”mining” tool, selecting the features that discrim-

inate between classes of images. This is the funda-

mental relationship that characterizes image retrieval

as a potential knowledge discovery methodology. In

this work, objects were described as vectors of k-

curvatures (1) taken at each matched point of the sub-

jects, after being registered to the reference.

3.4 Image Retrieval

In a CBIR system, the user presents an image as a

query, which is registered to the reference image. The

features obtained from the resulting mapping func-

tion are compared to the features of the images in the

database, which have been previously processed and

registered to the same reference. Following a measure

of similarity, the most similar images are retrieved and

presented to the user.

The model used to determine the similar-

ity between two images was the Euclidean dis-

tance (Del Bimbo, 1999). If q is the feature vector

representing the query and v

is the feature vector rep-

resentation of image k in the database, the similarity

between them can be computed as

sim(v

,q) = ((v

−q)

−q))

1/2

The performance of an image retrieval system can

be evaluated by computing two metrics (Del Bimbo,

1999): The recall of the system is the ability to re-

trieve relevant images. It is deﬁned as the ratio be-

tween the number of retrieved images considered rel-

evant and the total number of relevant images in the

database. The precision reﬂects the ability of the sys-

tem to retrieve only relevant images. It is deﬁned as

REGISTRATION AND RETRIEVAL OF ELONGATED STRUCTURES IN MEDICAL IMAGES

149

the ratio between the number of retrieved images con-

sidered relevant and the total number of retrieved im-

ages. The plot of recall × precision gives an estimate

of the overall effectiveness of a CBIR system, as a

compromise between both performance metrics is ex-

pected.

4 EXPERIMENTS

We illustrate the proposed registration-based retrieval

system with a case study on the morphology of the

corpus callosum in the chromosome 22q11.2 dele-

tion syndrome (DS22q11.2). The DS22q11.2 is an

example of genetic abnormality for which many hy-

potheses on anatomical differences have been re-

cently stated (Machado et al., 2007). This syndrome

is the result of a 1.5 - 3Mb microdeletion on the

long arm of chromosome 22 and is characterized by

a range of medical manifestations that include car-

diac, palatal and immune disorders, as well as par-

ticular problems in cognitive domains associated with

the orienting and executive attention systems and with

numerically related processing. Recent studies have

drawn particular attention to changes in the corpus

callosum — the largest bundle of axons connecting

the two hemispheres of the brain, as differences in the

shape of this structure may indicate changes in brain

connectivity that may be related to the observed cog-

nitive impairments (Simon et al., 2005). We hypothe-

sized that an image retrieval system would be able to

retrieve images of subjects sharing the same diagno-

sis, based on a shape representation of the corpus cal-

losum, if the features used to index the images could

be considered discriminative for the syndrome. In this

sense, the system would reveal the most distinguish-

ing features associated with the disease.

Participants in this study were 18 children with

chromosome 22q11.2 deletion syndrome, ranging in

age from 7.3 to 14.0 years (mean,S.D.=9.9,1.4 years)

and 18 typically developing control children, ranging

in age from 7.5 to 14.2 years (mean,S.D.=10.4,2.0

years) (Simon et al., 2005). Magnetic resonance

imaging was performed on a 1.5 Tesla Siemens MAG-

NETOM Vision scanner (Siemens Medical Solutions,

Erlangen, Germany). For each subject, a high-

resolution three-dimensional structural MRI was ob-

tained using a T1-weighted magnetization prepared

rapid gradient echo (MP-RAGE) sequence with the

following parameters: repetition time (TR) = 9.7 ms,

echo time (TE) = 4 ms, ﬂip angle = 12(, number of

excitations = 1, matrix size = 256x256, slice thick-

ness = 1.0 mm, 160 sagittal slices, in-plane resolution

= 1x1 mm. The midsagittal slice of each brain im-

(a) (b)

(c)

(d)

(e)

Figure 4: An example of registration. The midline and

boundary of the reference (a) is registered to the subject (b)

and the result interpolated to the whole structure (c). The

original plot of the boundary curvatures (d) and result of

registration (e) are also shown, where the curvatures of the

template and subject are represented by thick and thin lines,

respectively. The 7 landmarks used for registration evalu-

ation, numbered from left to right, are depicted in (a) with

thick lines.

age volume was manually extracted as the best plane

spanning the interhemispheric ﬁssure, and on which

the anterior and posterior commissures and the cere-

bral aqueduct were visible.

The callosa in the midsagittal images were seg-

mented by manual thresholding and delineation. The

boundaries of the callosa were automatically deter-

mined using the Rosenfeld algorithm for 8-connected

contours (Gonzalez and Woods, 2002). The midlines

of the callosa were also extracted based on the algo-

rithm proposed in Section 3.1 and interpolated so as

to yield an isotropic rotation-invariant representation,

in which any two consecutive sampled points were 1

mm apart. The pointwise curvature of the callosum

midline was computed for each subject, using the k-

curvature metric (1), where k was empirically chosen

to be 10% of the length of the midline, so as to pro-

vide enough smoothness.

Shape measurement was performed, by aligning

a reference image of the callosum to subject callosa.

One of the control subjects was arbitrarily chosen as

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

150

the reference. The midline of the reference, sampled

at 87 equidistant points, was registered to the sub-

jects’ midlines based on the cost function described in

(2) with parameters α=0.001, β=1000.0 and γ

=-1.0

/degree

for i ∈ {M,D,V }, which were empiri-

cally determined. The midline curves of the subject

callosa were interpolated to provide sub-pixel preci-

sion (0.5 mm). The result of registration was a map-

ping from each of the 87 points in the reference to cor-

responding points in the subjects. Registration took

7.78 seconds to compute. All methods were imple-

mented in IDL language (Research Systems) and run

in a 1.1 GHz Intel Celeron processor computer with

256 MB of RAM, under Windows XP operating sys-

tem.

Figure 4 shows an example of registration where

the reference image described through its midline and

perpendicular segments (a) is deformed to match the

subject (b). The resulting deformation is shown as a

warped grid (c). A plot of the original k-curvatures

(in degrees/mm) at the boundaries of both images

(in mm), taken counterclockwise from the leftmost

endpoint of the midline, is given in (d) and the re-

sulting registration is depicted in (e). The effective-

ness of registration was evaluated based on 2 sets

of landmarks provided by an expert, taken in an in-

terval of 2 weeks. Seven landmarks were deﬁned

at the reference, from anterior to posterior callosum

(Figure 4a), and the expert was asked to determine

their corresponding loci at each of the 36 subjects.

The set of 504 landmarks were compared to the re-

sults of registration. Table 1 summarizes the results,

where it is possible to compare the average error of

the method with the variability of measures provided

by the expert, for each landmark. The average error

of the method for the whole set of landmarks was 1.7

mm, a satisfactory result considering that the aver-

age variability of the expert’s measures was 1.2 mm.

Larger errors were observed at landmarks 3 and 4

(callosal body) where the subjects present larger vari-

ability with respect to curvature. The best results were

achieved at landmarks 5 and 6 (posterior callosum)

where the errors obtained with automatic registration

were smaller than the average variability observed in

manual registration.

The results of image retrieval were evaluated with

the aid of a simple retrieval environment. Initially,

the user browses the database and chooses an image

that will represent the query. The system ranks the

remaining images, showing the n most relevant to the

user appraisal. In this study, we considered as rele-

vant the images that shared the same diagnosis of the

query (with or without the deletion). Following the

recent ﬁndings on anatomic differences in the callo-

sum of these populations (Machado et al., 2007)(see

Figure 5), an effective CBIR should be able to re-

trieve images sharing the same diagnosis, unless out-

liers would be present in the database.

(a) (b)

Figure 5: Mean callosal shape for the typically developing

children (a) and children with the deletion (b). Controls

have shorter, more curved anterior callosum (rostrum and

genu) and less curved midbody. Children with the deletion

present more arched callosum (larger height/length ratio).

Table 1: Average error (mm) for each landmark, consider-

ing manual and automatic registration.

Landmark 0 1 2 3 4 5 6

Manual 0.6 0.4 0.7 1.7 1.3 2.6 1.0

Automatic 1.0 0.9 0.8 3.7 2.4 1.6 0.9

An example of the results of image retrieval is

shown in Figure 6. The query image presented by

the user (a) is registered to the same reference used in

the registration of the images stored in the database.

The 10 images that yield greater similarity with re-

spect to the curvature of the midline and boundary are

retrieved and displayed (b). Images of controls are

shown in gray and images of children with the dele-

tion are shown in black. A plot of the recall × pre-

cision computed after the retrieval of each of the 17

relevant images in the database is presented in (d). In

this case, the query is a typical control, yielding high

precision.

An example in which an outlier is retrieved is

given in Figure 7. The third retrieved image is a con-

trol with arched callosum, whereas the query is a child

with the deletion. In this case, the precision is af-

fected. Worse result occurs when the query itself is

an outlier, as exampled in Figure 8. In this case, the

query is a control with longer, less curved rostrum

(left-most end of the midline) that is more common

in children with the deletion. As a consequence, the

precision is drastically affected, staying bellow 50%

from the second retrieved image, a level that would

be expected by pure chance.

5 CONCLUSIONS

We have addressed the problem of registering and re-

trieving images of elongated structures. Traditional

REGISTRATION AND RETRIEVAL OF ELONGATED STRUCTURES IN MEDICAL IMAGES

151

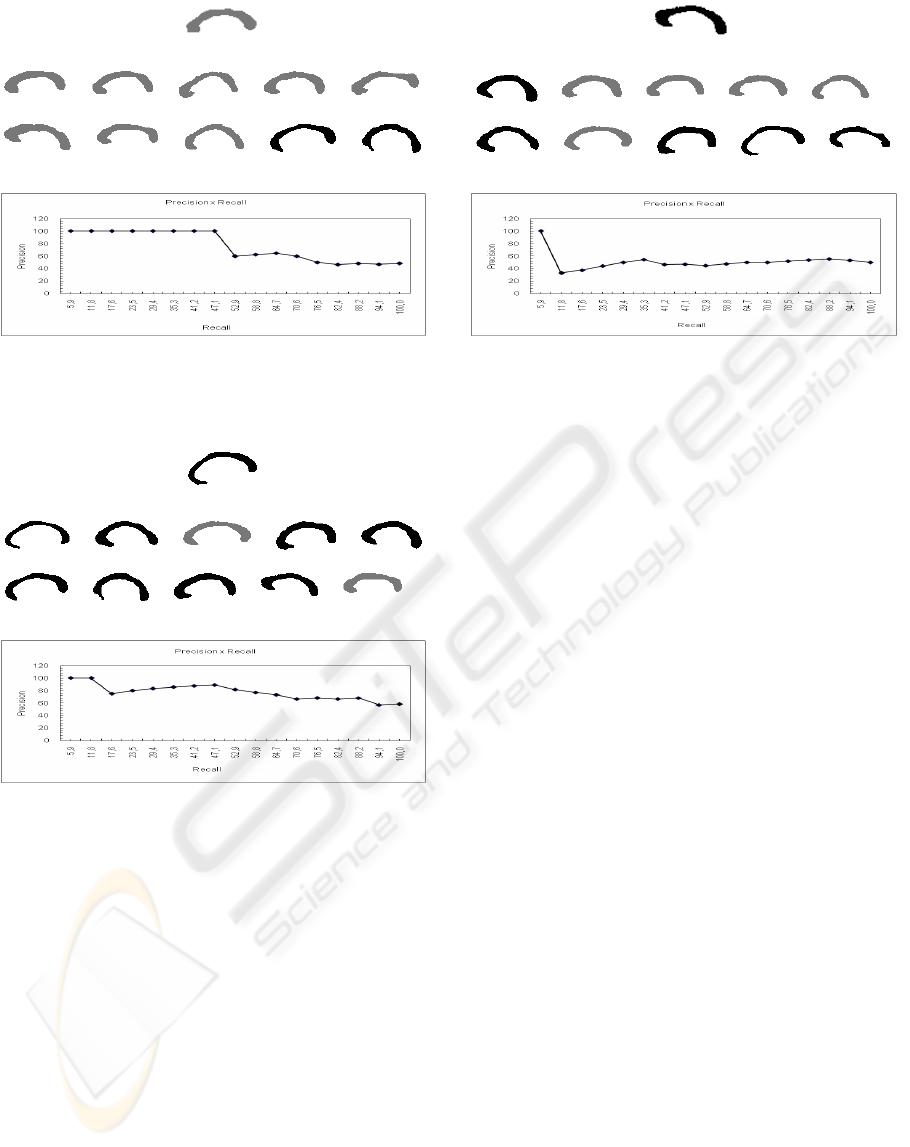
(a)

(b)

(c)

Figure 6: Example of a query image (a) and the result of

retrieval (b). The plot of recall × precision is shown in (c).

(a)

(b)

(c)

Figure 7: Example of a query image (a) and the result of

retrieval (b). In this case, the third best-ranked image is an

outlier. The plot of recall × precision is shown in (c).

registration methods may yield anatomically incon-

sistent results while applying warping models only to

the structure’s contour or medial axis. The method

proposed in this paper jointly registers the medial

axis, dorsal and ventral boundaries, avoiding distor-

tions that may impact substantially in the results of

further morphometric analyses, hypothesis testing or

image retrieval.

The method deserves more systematic evaluation

procedures, as visual inspection is subjective and dif-

ﬁcult to quantify. A case study on the morphology of

the corpus callosum in the 22q11.2 deletion syndrome

was used to illustrate the ability of registration to pro-

vide effective image retrieval. In the experiments, di-

agnosis was considered as the ground truth to evalu-

(a)

(b)

(c)

Figure 8: Example of a query image (a) and the result of

retrieval (b). In this case, the query is an outlier, yielding

poor performance (c).

ate the performance of the retrieval system. Although

evidences of shape differences between controls and

children with the deletion exist, outliers make eval-

uation a difﬁcult task. A deﬁciency of the method

is the requirement for manual choice of the midline

endpoints, so a fully automated algorithm is already

being designed. Another well-known disadvantage of

registration-driven retrieval methods is its inadequacy

to indexing, limiting the application of these systems

to small datasets. Furthermore, the vector model that

exhibits excellent performance in text retrieval is not

a consensus when dealing with images.

Relevance feedback is an important step that de-

serves attention. Different similarity functions and

query updating models may enhance the effectiveness

of image retrieval, as the user’s preferences are more

rapidly met. Experiments have shown that when the

set of features is restricted to speciﬁc regions of in-

terest, the precision is enhanced. In the case of the

study on the corpus callosum morphometry, restrict-

ing the computation of similarity to the anterior-most

part of the structure, where the differences between

groups are more evident, has increased the number of

retrieved images that share the same diagnosis. This

ability to cluster images of the same group may qual-

ify image retrieval as a potential knowledge discovery

tool. It implements new levels of supporting environ-

ments and opens new perspectives to exploratory re-

search in image databases.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

152

ACKNOWLEDGEMENTS

This work was partially supported by FAPEMIG,

PUC Minas and CNPq grant 20043054198. The au-

thors are grateful to the University of Pennsylvania

for sharing the corpus callosum data.

REFERENCES

Barrodale, I., Skea, D., Berkley, M., Kuwahara, R., and

Poeckert, R. (1993). Warping digital images using thin

plate splines. Pattern Recognition, 26(2):375–376.

Blum, H. and Nagel, R. N. (1978). Shape description using

weighted symmetric axis features. Pattern Recogni-

tion, 10(3):167–180.

Cootes, T., Hill, A., Taylor, C. J., and Haslam, J. (1994).

Use of active shape models for locating structures

in medical images. Image and Vision Computing,

12(6):355–365.

Davatzikos, C. and Prince, J. (1995). An active contour

model for mapping the cortex. IEEE Transactions on

Medical Imaging, 14:65–80.

Del Bimbo, A. (1999). Visual Information Retrieval. Mor-

gan Kaufman.

Dvies, E. R. and Plummer, A. P. (1981). Thinning algo-

rithms: a critique and a new methodology. Pattern

Recognition, 14:53–63.

Golland, P., Grimson, W. E. L., and Kikinis, R. (1999). Sta-

tistical shape analysis using ﬁxed topology skeletons:

Corpus callosum study. Lecture Notes in Computer

Science, 1613:382–387.

Gonzalez, R. C. and Woods, R. E. (2002). Digital Image

Processing. Prentice-Hall, Upper Saddle River.

Hamarneh, G., Abu-Gharbieh, R., and McInerney, T.

(2004). Medial proﬁles for modeling deformation and

statistical analysis of shape and their use in medical

image segmentation. International Journal of Shape

Modeling, 10(2):187–209.

Lew, M., Sebe, N., Djeraba, C., and Jain, R. (2006).

Content-based multimedia information retrieval: State

of the art and challenges. ACM Transactions on Mul-

timedia Computing, Communications, and Applica-

tions, 2(1):1–19.

Machado, A., Simon, T., Nguyen, V., McDonald-McGinn,

D., Zackai, E., and Gee, J. (2007). Corpus cal-

losum morphology and ventricular size in chromo-

some 22q11.2 deletion syndrome. Brain Research,

1131:197–210.

McInerney, T. and Terzopoulos, D. (1996). Deformable

models in medical image analysis: A survey. Medi-

cal Image Analysis, 1(2):91–108.

Muller, H., Michoux, N., Bandon, D., and Geissbuhler, A.

(2004). A review of content-based image retrieval sys-

tems in medical applications-clinical beneﬁts and fu-

ture directions. International Journal of Medical In-

formatics, 73(1):1–23.

Pizer, S. M., Fletcher, P. T., Joshi, S., Thall, A., Chen, J. Z.,

Fritsch, D. S., Gash, A. G., Glotzer, J. M., Jiroutek,

M. R., Lu, C., Muller, K. E., Tracton, G., Yushkevich,

and Chaney, E. (2003). Deformable m-reps for 3D

medical image segmentation. International Journal

of Computer Vision, 55(2):85–106.

Pizer, S. M., Fritsch, D. S., Yushkevich, P., Johnson, V.,

and Chaney, E. (1996). Segmentation, registration

and measurement of shape variation via image ob-

ject shape. IEEE Transactions on Medical Imaging,

18(10):851–865.

Simon, T. J., Ding, L., Bish, J. P., McDonald-McGinn,

D. M., Zackai, E. H., and Gee, J. C. (2005). Volu-

metric, connective, and morphologic changes in the

brains of children with chromosome 22q11.2 deletion

syndrome: an integrative study. Neuroimage, 25:169–

180.

Smeulders, A., Worring, M., Santini, S., Gupta, A., and

Jain, R. (2000). Content-based image retrieval at the

end of the early years. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, 22(12):1349–

1380.

Staal, J. (2004). Segmentation of elongated structures in

medical imaging. PrintPartners Ipskamp, Enschede.

Toga, A. W. (1999). Brain Warping. Academic Press, New

York.

Toledo, R., Orriols, X., Binefa, X., Radeva, P., Vitria, J., and

Villanueva, J. (2000). Tracking of elongated structures

using statistical snakes. In Proceedings of the CVPR,

pages 157–162, Hilton Head Island.

Xie, J. and Heng, P. A. (2005). Shape modeling using au-

tomatic landmarking. Lecture Notes in Computer Sci-

ence, 3750:709–716.

Yushkevich, P., Fletcher, P. T., Joshi, S., Thall, A., and Pizer,

S. (2003). Continuous medial representations for geo-

metric object modeling in 2d and 3d. Image and Vision

Computing, 21(1):17–28.

REGISTRATION AND RETRIEVAL OF ELONGATED STRUCTURES IN MEDICAL IMAGES

153