NONLINEAR MODELING OF CARDIOVASCULAR

RESPONSE TO EXERCISE

Lu Wang

, Steven W. Su

2,1

, Gregory S. H. Chan

, Branko G. Celler

*, Teddy M. Cheng

and Andrey V. Savkin

Biomedical System Lab, School of Electrical Engineering & Telecommunications, Faculty of Engineering

University of New South Wales, UNSW Sydney, N.S.W. 2052, Australia

Key University Research Centre for Health Technologies, Faculty of Engineering, University of Technology

Sydney,PO Box 123 Broadway NSW 2007 Australia

Keywords: Cardiovascular system, Nonlinear modelling, Cardiovascular responses to Exercise, Machine learning.

Abstract: This study experimentally investigates the relationships between central cardiovascular variables and

oxygen uptake based on nonlinear analysis and modeling. Ten healthy subjects were studied using cycle-

ergometry exercise tests with constant workloads ranging from 25 Watt to 125 Watt. Breath by breath gas

exchange, heart rate, cardiac output, stroke volume and blood pressure were measured at each stage. The

modeling results proved that the nonlinear modeling method (Support Vector Regression) outperforms

traditional regression method (reducing Estimation Error between 59% and 80%, reducing Testing Error

between 53% and 72%) and is the ideal approach in the modeling of physiological data, especially with

small training data set.

1 INTRODUCTION

The relationships between central cardiovascular

variables and oxygen uptake during steady state of

graded exercise have been widely examined by

numerous investigators (Allor et al., 2000) (Astrand

et al., 1964) (Fairbarn et al., 1994) (Freedman et al.,

1955) (Kobayashi et al., 1978) (Reeves et al., 1961)

(Richard et al., 2004) (Rowland et al., 1997) (Turley

et al., 1997). Most of them investigated the

relationship between cardiac output (CO) and

oxygen uptake (



) using linear regression

methods and found the slope between the two

variables to be approximately 5 – 6 in normal and

athletic subjects (Rowell et al., 1986). Beck et al

(Beck et al., 2006) in contrast, investigated this

relationship in healthy humans using polynomial

regression. Turley (Turley et al., 1997) described

both the relationship of stroke volume (SV) and the

total peripheral resistance (TPR) to oxygen uptake

during steady state of sub-maximal exercise using

linear regression. However, from the point view of

modeling, the regression methods used by the

previous researchers have several limitations. First

the empirical risk minimization (ERM) principle

used by traditional regression models does not

guarantee good generalization performance and may

produce models that over-fit the data (Gunn, 1997).

Secondly, most of the regression models developed

from early research based on a small sample set with

limited subjects during three or four exercise

intensities. Traditional regression approachs are

particularly not recommended for modeling small

training sets. Determination of the size of the

training set is a main issue to be solved in the

modeling performance because the sufficiency and

efficiency of the training set is one of the most

important factors to be considered.

This study presents a novel machine learning

approach, Support Vector Regression (SVR)

(Drucker et al., 1997) to model the central

cardiovascular response to exercise. SVR, developed

by Vapnik and his co-workers in 1995, has been

widely applied in forecasting and regression (Su et

al., 2007) (Su et al., 2005) (Su et al., 2006) (Valerity

et al., 2003). The following characteristics of SVR

make it an ideal approach in modeling of

cardiovascular system. Firstly, SVR avoids the over-

fitting problem which exists in the traditional

modeling approaches. Second, SVR condenses

information in the training data and provide a sparse

Wang L., W. Su S., S. H. Chan G., G. Celler B., M. Cheng T. and V. Savkin A. (2008).

NONLINEAR MODELING OF CARDIOVASCULAR RESPONSE TO EXERCISE.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 40-46

DOI: 10.5220/0001059000400046

 SciTePress

representation by using a small number of data

points (Girosi, 1998). Thirdly, SVR is insensitive to

modeling assumption due to its being a non-

parametric model structure. Finally, the SVR model

is unique and globally optimal, unlike traditional

training which can risk converging to local minima.

The rest of this paper is organized as follows:

section 2 describes the experimental design for the

data collection. Section 3 applies SVR for modeling

the relationships between central cardiovascular

variables and oxygen uptake. Finally, some

conclusions are drawn in Section 4.

2 EXPERIMENTAL DESIGN

2.1 Subjects

We studied 12 normal male subjects. They are all

active, but do not participate in formal training or

organized sports. However, since two of them could

not complete 6 minutes of higher level exercise, only

the data recorded from 10 subjects (aged 25 ± 4yr,

height 177 ± 5cm, body weight 73 ± 11kg) are used

for this study. All the subjects knew the protocol and

the potential risks, and had given their informed

consent.

2.2 Experimental Procedure

All tests were conducted in the afternoon in an air-

conditioned laboratory with temperature maintained

between 23-24

C. The subjects were studied during

rest and a series of exercise in an upright position on

an electronically braked cycle ergometer. Exercise

was maintained at a constant workload for 6

minutes, followed by a period of rest. The initial

exercise level was 25W and each successive stint of

exercise was increased in 25W steps until a

workload of 125W was reached. The rest periods

were increased progressively from 10 to 30 minutes

after each stint of exercise. Six minutes of exercise

was long enough to approach a steady state since the

values of oxygen uptake and the A-V oxygen

difference had become stable by the 5th and 6th

minutes even for near maximum exertion (Reeves et

al., 1961).

2.3 Measurement and Data Processing

Heart rate was monitored beat by beat using a single

lead ECG instrument, while ventilation and

pulmonary exchange were measured on a breath by

breath basis. Minute ventilation was measured

during inspiration using a Turbine Flow Transducer

model K520-C521 (Applied Electrochemistry,

USA). Pulmonary gas exchange was measured using

S-3A and CD-3A gas analyzers (Applied

Electrochemistry, USA). Before each individual

exercise test, the turbine flow meter was calibrated

using a 3.0 liters calibration syringe. Before and

after each test, the gas analyzers were calibrated

using reference gases with known O

and CO

concentrations. The outputs of the ECG, the flow

transducer and the gas analyzers were interfaced to a

laptop through an A/D converter (NI DAQ 6062E)

with a sampling rate of 500 Hz. Programs were

developed in Labview 7.0 for breath by breath

determination of pulmonary gas exchange variables

but with particular reference to



(



STPD).

Beat by beat stroke volume and cardiac outputs were

measured noninvasively using the ultrasound based

device (USCOM, Sydney, Australia) at the

ascending aorta. This device has previously been

reported to be both accurate and reproducible

(Knobloch et al., 2005). In order to keep consistent

measurements, all CO/SV measurements were

conducted by the same person. An oscillometric

blood pressure measurement device (CBM-700,

Colin, France) was used to measure blood pressure.

The measurement of



and HR were

conducted during the whole exercise and recovery

stage. The static values (



and HR) were

calculated for each workload from data collected in

the last minute of the six minute exercise protocol.

The measurements of SV, CO and BP (blood

pressure) were similarly conducted during the last

minute of the six minute exercise for each workload

with the additional requirement that subjects keep

their upper body as still as possible to minimize

artifacts caused by the movement of the chest during

exercise. We then, calculated their static values (CO,

SV and BP) based on the measurement in the last

minute for each workload.

2.4 Results

We found that the percentage changes of

cardiovascular variables relative to their rest values

more uniform than when absolute values are used.

This may be because using relative values diminish

the variability between subjects. For example,

Figure 1 (a) shows the relationship between the

absolute value of mean arterial blood pressure

response and the absolute value of oxygen uptake

rate for all the ten subjects, while Figure 1 (b) is the

percentage change in mean arterial blood pressure

relative to its rest value with the percentage change

in oxygen uptake rate to its rest value for the ten

NONLINEAR MODELING OF CARDIOVASCULAR RESPONSE TO EXERCISE

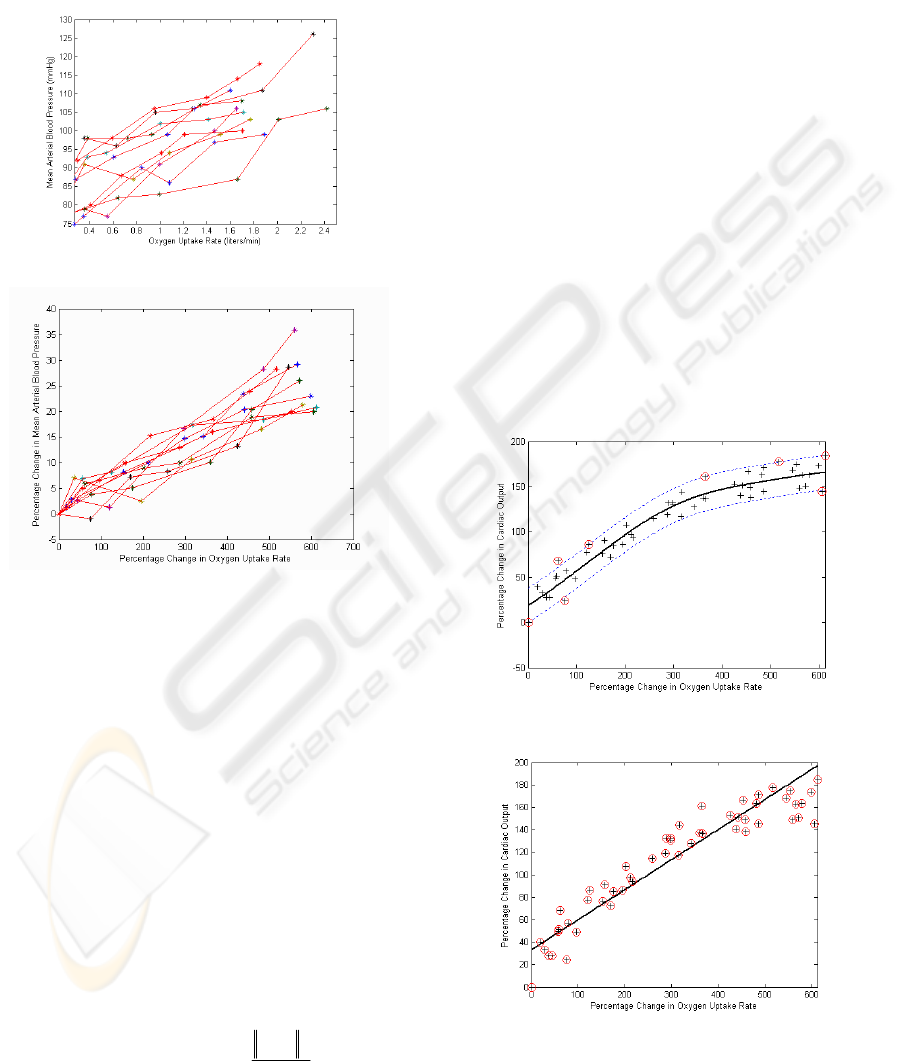
subjects. Obviously, the response in Figure 1 (b) is

more consistent and gives clearer trend than that in

Figure 1 (a). It is thus reasonable to believe that

modeling of cardiovascular responses using relative

changes may give more robust results than modeling

with the absolute values.

(a). Mean arterial blood pressure response to oxygen

uptake rate (in absolute value).

(b). Mean arterial blood pressure response to oxygen

uptake rate (in relative value).

Figure 1: Mean arterial blood pressure response to oxygen

uptake rate for the ten subjects.

Based on the above finding, we model CO, SV

and TPR to



by modeling the percentage

changes in CO, SV and TPR with respect to their

corresponding rest values to percentage change in



with respect to its rest value. We use CO%,

SV%, TPR% and



% to represent their relative

values (expressed as percentage), respectively.

3 APPLICATION OF SVR FOR

MODELING

We selected radial basic function (RBF) kernels for

this study, that is

)

exp(),(

xxK

−

−=

where

the kernel parameter,

x is the ith input support

value and

is the input value.

Detailed discussion about SVR, such as the

selection of regularization constant

, radius

the tube and kernel function, can be found in (Gunn,

1997) (Vapnik, 1998).

In order to show the effectiveness of SVR, we

applied both SVR and traditional linear regression

(Least-Square linear regression (LS)) to investigate

the relationships between percentage change of

cardiovascular variables (CO%, SV% and TPR%)

and



3.1 The Relationship between CO%

and



3.1.1 Model Identification

A SVR model was developed to estimate CO% from



% (Table 1 and Figure 2). Although it is widely

accepted that there is a linear relationship between

cardiac output and oxygen consumption (Allor et al.,

2000) (Astrand et al., 1964) (Freedman et al., 1955),

(a). Estimation of percentage change in CO from

percentage change in



using SVR.

(b). Estimation of percentage change in CO from

percentage change in



using LS.

Figure 2: Comparison of estimation results of CO%

between using SVR and using LS.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

their relationship can be better described by the

nonlinear SVR model in terms of reducing the errors

(MSE) from 418 to 171 (Table 2), an improvement

of 59% comparing with that of LS method

The results in Table 1 also show the efficiency of

SVR. Unlike traditional regression method where

the solution of the model depends on the whole

training data points, in SVR, the solution to the

problem is only dependent on a subset of training

data points which are referred to as support vectors.

Using only support vectors, the same solution can be

obtained as using all the training data points. SVR

uses just 13% of the total points available to model

their nonlinear behavior efficiently.

3.1.2 Model Validation

To further evaluate the feasibility of this proposed

SVR model, the whole data set is divided into two

parts: the first part (70% of the data) is used to

design the model and the second part (30% of the

data) is used to test its performance. Because we do

not have large sample of data, we separated the data

set into two parts randomly five times. Each time we

use 70% of the data for training and the rest for

testing. We established the SVR model with the

three design parameters (kernel function, capacity

(

C ) and the radius of insensitivity (

)) based on

the training set, and test its goodness on the testing

set. In Figure 3, we present the results for one of the

5 tests. As shown in Table 3, the averaged results

(MSE) for the 5 times testing for SVR is 245±15.

However, the averaged error for traditional linear

regression is as high as 521±19. It indicates that

SVR can build more robust models to predict CO%

from



% using only a small training set. It also

demonstrates that SVR can overcome the over-

fitting problem, even though SVR has more model

parameters than the traditional linear regression

method.

3.2 The Relationship between SV%

and



Figure 4 shows the models for estimating SV%. The

SVR model gives more precisely estimation than the

LS does and decreases estimation errors (MSE) by

67% (Table 2).

The testing models are given in Figure 5 and the

testing errors are in Table 3. As indicated, the SVR

model decreases the testing error by 64%.

(a). Testing of SVR model.

(b). Testing of LS model

Figure 3: Comparison of models of CO% against %

change in oxygen uptake using SVR and using LS

methods.

(a). Estimation of percentage change in SV from

percentage change in



using SVR.

(b). Estimation of percentage change in SV with percentage

change in



using linear regression.

Figure 4: Comparison of estimation results for SV%

between using SVR and using LS.

NONLINEAR MODELING OF CARDIOVASCULAR RESPONSE TO EXERCISE

(a). Testing of SVR model.

(b). Testing of LS model.

Figure 5: Comparison of the testing results for Stroke

Volume using SVR and using traditional linear regression.

3.3 The Relationship between TPR%

and



As shown in Figure 6, the SVR model describes a

rapid fall in TPR% at low workloads which remains

relatively constant even with increasing



%. SVR

uses just 13% (Table 1) of the total points to get an

efficient nonlinear model. Compared with linear

regression, the SVR model decreases MSE from 151

to 30, an improvement of 80%.

The testing results for this SVR model and the

equivalent LS model are given in Figure 7 and Table

3, respectively. Both of these (Figure 7 and Table 3)

demonstrate that SVR outperforms the traditional

linear regression method by reducing testing errors

significantly, from 130 to 36.

(a). Estimation of percentage change in TPR from

percentage change in



using SVR.

(b). Estimation of percentage change in TPR with

percentage change in



using linear regression.

Figure 6: Comparison of the estimation results of TPR%

between using SVR and LS.

(a). Testing of SVR model.

(b). Testing of LS model.

Figure 7: Comparison of the test results of TPR% against

% change on Oxygen uptake using SVR and using LS.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

Table 1: Fitting data for the model of cardiovascular

variables and oxygen uptake rate using SVR.

Relation

CO% Vs



SV% Vs



TPR%



Kernel RBF RBF RBF

Parameter σ = 200 σ = 500 σ = 500

Regularization

constant C

5000 5000 5000

ε-insensitivity 19 3 8

Support

vectors

number

8 (13.3%)

(13.3%)

8 (13.3%)

Estimation

error

171 5 30

Table 2: Comparison of the estimation errors (MSE)

between using SVR and using linear regression method

Relation

CO% Vs



SV% Vs



TPR% Vs



SVR 171 5 30

LS 418 15 151

Table3: Comparison of the model fitting errors (MSE)

using SVR and linear regression methods (N=5).

Relation

CO% Vs



SV% Vs



TPR%



SVR testing

error

245 ± 15 8 ± 2 36 ± 5

LS Testing

error

521 ± 19 22 ± 7 130 ± 12

4 CONCLUSIONS

This is the first time that SVR has been applied to

experimentally investigate the steady state

relationships between key central cardiovascular

variables and oxygen consumption during

incremental exercise. The impressive results

obtained prove that SVR is an effective approach

that can be recommended for the modeling of

physiological data.

ACKNOWLEDGEMENTS

The authors acknowledge project DP0452186/2003

funded by ARC (Australian Research Council).

REFERENCES

Allor KM, Pivarnik JM, Sam LJ et al (2000) Treadmill

economy in girls and women matched for height and

weight. J. Appl. Physiol 89: 512-516.

Astrand PO, Cuddy TE, Saltin, B et al (1964) Cardiac

output during submaximal and maximal work. J. Appl.

Physiol 9: 268-274.

Beck KC, Randolph LN, Bailey KR et al (2006)

Relationship between cardiac output and oxygen

consumption during upright cycle exercise in healthy

humans. J. Appl. Physiol 101: 1474 – 1480.

Drucker H, Burges C, Kaufman L et al (1997) Support

vector regression machines. In: Advances in Neural

Information Procession Systems, edited by M. Mozer,

M. Jordan & T. Petsche. Cambridge, MA. p. 155-161.

Fairbarn MS, Blackie SP, McElvaney NG et al (1994)

Prediction of heart rate and oxygen uptake during

incremental and maximal exercise in healthy adults.

Chest 105: 1365-1369.

Freedman ME, Snider GL, Brostoff P et al (1955) Effects

of training on response of cardiac output to muscular

exercise in athletes. J. Appl. Physiol 8:37-47.

Girosi F (1998) An equivalence between sparse

approximation and support vector machines. Neural

Computation, 20, 1455-1480.

Gunn SR (1997) Support Vector Macines for

classificationa and regression, Technical Report,

Department of Electronics and Computer Science,

University of Southampton.

Knobloch K, Lichtenberg A (2005) Winterhalter M,

Rossner D, Pichlmaier M,. and Philips R. Non-

invasive cardiac output determination by two-

dimensional independent Doppler during and after

cardiac surgery. Ann Thorac Surg 80: 1479-1483.

Kobayashi Y, Andoh Y, Fujinami T et al (1978)

Impedance cardiography for estimating cardiac output

during submaximal and maximal work. J. Appl.

Physiol 45: 459-462.

Reeves JT, Grover RF, Blount SG Jr et al (1961) Cardiac

output response to standing and treadmill walking. J.

Appl. Physiol 16: 283-288.

Reeves JT, Grover RF, Filley GF et al (1961) Circulatory

changes in man during mild supine exercise. J. Appl.

Phsiol 16: 279-282.

Richard R, Lonsdorfer-wolf E, Dufour S et al (2004)

Cardiac output and oxygen release during vintensity

exercise performed until exhaustion. Eur J Appl

Physiol 93: 9-18.

Rowell LB. Circulatory adjustments to dynamic exercise

(1986) In: Human circulation regulation during

physical stress. New York: Oxford University Press,

p. 213-256.

Rowland T, Popoeski , Ferrone L (1997) Cardiac response

to maximal upright cycle exercise in healthy boys and

men. Med Sci Sport Exer 29:1146-1151.

Su SW, Wang L, Celler BG (2006), Estimation of Oxygen

Consumption for Moderate Exercises by Using a

Hammerstein Model, In Proceeding of the 28th

Annual International Conference of the IEEE

NONLINEAR MODELING OF CARDIOVASCULAR RESPONSE TO EXERCISE

Engineering in Medicine and Biology Society, New

York, USA, September, pp. 3427-3430.

Su SW, Wang L, Celler BG, Savkin AV, and Guo Y

(2007). Identification and Control for Heart Rate

Regulation during Treadmill Exercise, IEEE

Transactions on Biomedical Engineering 54 (7): 1238-

1246.

Su SW, Wang L, Celler B et al (2005) Estimation of

walking energy expenditure by using support vector

regression. In Proceedings of the 27th Annual

International Conference of the IEEE Engineering in

Medicine and Biology Society (EMBS), pp. 3526–

3529, Shanghai, China.

Turley KR, Wilmore JH (1997) Cardiovascular responses

to treadmill and cycle ergometer exercise in children

and adults. J. Appl. Physiol 83: 948-957.

Valerity VG, Supriya BG (2003) Volatility forecasting

from multiscale and high-dimensional market data.

Neurocomputing, 55, 285-305.

Vapnik V (1998) Statistical learning theory. New York:

Wiley.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing