NONLINEAR MODELLING AND CONTROL OF HEART RATE
RESPONSE TO TREADMILL WALKING EXERCISE
Teddy M. Cheng, Andrey V. Savkin, Branko G. Celler
School of Electrical Engineering and Telecommunications, the University of New South Wales, Sydney, NSW 2052, Australia
Steven W. Su
Faculty of Engineering, the University of Technology, Sydney, NSW 2007, Australia
Lu Wang
School of Electrical Engineering and Telecommunications, the University of New South Wales, Sydney, NSW 2052, Australia
Keywords:
Heart rate modelling, heart rate control, nonlinear systems, exercise physiology.
Abstract:
In this study, a nonlinear system was developed for the modelling of the heart rate response to treadmill
walking exercise. The model is a feedback interconnected system which can represent the neural response
and peripheral local response to exercise. The parameters of the model were identified from an experimental
study which involved 6 healthy adult male subjects, each completed 3 sets of walking exercise at different
speeds. The proposed model will be useful in explaining the cardiovascular response to exercise. Based on
the model, a 2-degree-of-freedom controller was developed for the regulation of the heart rate response during
exercise. The controller consists of a piecewise LQ and an H
∞
controllers. Simulation results showed that the
proposed controller had the ability to regulate heart rate at a given target, indicating that the controller can play
an important role in the design of exercise protocols for individuals.
1 INTRODUCTION
During dynamic exercise, the cardiovascular system
increases the delivery of blood and oxygen to working
muscles as the metabolic demand increases, resulting
in an increase in heart rate (HR) and stroke volume.
Obtaining a model that describes the HR response to
exercise will improve our understanding of exercise
physiology. Understanding the aetiology of HR re-
sponse during, and recovery after an exercise, may
also be beneficial to predicting cardiovascular disease
mortality (Savonen et al., 2006) (Cole et al., 1999).
This may also lead to an improvement in develop-
ing training protocols for athletics and more efficient
weight loss protocols for the obese, and in facilitating
assessment of physical fitness and health of individ-
uals (Achten and Jeukendrup, 2003). Furthermore,
knowing the cardiovascular system responses to the
stress induced by physical exercise provides us an-
other perspective on how this system functions. For
instance, this may give us some measures for the pre-
vention of cardiac failure from dialysis.
Studying and modelling of HR response during
exercise have been carried out by a number of re-
searchers (e.g. (Brodan et al., 1971; Hajek et al.,
1980; Rowell, 1993; Coyle and Alonso, 2001; Su
et al., 2007)). Broden et al. (Brodan et al., 1971) and
Hajek et al. (Hajek et al., 1980) modelled the HR re-
sponse from a regulation point of view. Their models
are reliable for short duration exercises, but are not
sufficient for explaining long duration exercises. As
shown in, e.g. (Coyle and Alonso, 2001), HR will
continue to increase during prolonged exercise. In
reference (Su et al., 2007), exercising HR response
was modelled by a Hammerstein system
1
. Besides
modelling, they also studied the control of the HR re-
sponse during exercise.
The ability to control the HR during exercise is
of importance in the design of exercise protocols for
patients with cardiovascular diseases and in develop-
ing rehabilitation exercises to aid patients recovering
from cardiothoracic surgery. The control of heart rate
response during exercise has been reported in the ref-
erences (Kawada et al., 1999; Cooper et al., 1998; Su
1
A system consists of a static nonlinearly cascaded at
the input of a linear system.
498
M. Cheng T., V. Savkin A., G. Celler B., W. Su S. and Wang L. (2008).
NONLINEAR MODELLING AND CONTROL OF HEART RATE RESPONSE TO TREADMILL WALKING EXERCISE.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 498-503
DOI: 10.5220/0001059104980503
Copyright
c
 SciTePress

et al., 2007). Among them, a number of different con-
trol strategies or algorithms have been successfully
applied, e.g. classical PID control, H
∞
control, and
model reference control. Each has its merits or disad-
vantages and therefore, it is interesting to investigate
the usefulness of other control algorithms and tech-
niques which have been developed by the control so-
ciety.
The objective of this paper is twofold. First,
a nonlinear model is proposed to describe the HR
response to treadmill walking exercise during both
the exercising and the recovery phases. We model
the HR response from the neural and the local re-
sponses perspective. The advantage of this approach
is that the model may describe the HR response over
a longer exercise duration. Secondly, using the pro-
posed model, we develop a controller-using the tread-
mill’s speed as a control variable-that regulates the
HR during exercise. The controller consists of feed-
forward and feedback components which provide bet-
ter performance without trading off robustness.
2 THE MODEL
In this paper, we propose the following nonlinear
state-space control systems to model the HR response
to treadmill walking exercise:
˙x
1
(t) = −a
1
x
1
(t) + a
2
x
2
(t) + a
2
u
2
(t)
˙x
2
(t) = −a
3
x
2
(t) + φ(x
1
(t))
y(t) = x
1
(t)
(1)
where φ(x
1
(t)) :=
a
4
x
1
(t)
1+exp

−15(x
1
(t)−a
5
)

and x(0) =
[x
1
(0) x
2
(0)]
T
= 0, y(t) describes the change in HR
from rest, and a
1
,...,a
5
are positive scalars. The con-
trol input u(t) represents the speed of the treadmill.
System (1) can be viewed as a feedback intercon-
nected system, i.e. x
1
in the forward path and x
2
in the
feedback path. The component x
1
(t) can be viewed as
the change of HR due to the neural response to exer-
cise, including both the parasympathetic and the sym-
pathetic neural inputs (see e.g. (Rowell, 1993)). The
component x
2
is utilised in describing the complex
slow-acting peripheral effects from, e.g. the hormonal
systems, the peripheral local metabolism, and/or the
increase in body temperature, etc.. Generally, these
effects cause vasodilatation and hence HR needs to
be increased in order to maintain the arterial pressure
(see (McArdle et al., 2007))). So, the feedback signal
x
2
, which can be thought of as a dynamic disturbance
input to the x
1
subsystem, is a reaction to the periph-
eral local effects. By observing system (1), the input
Table 1: Physical characteristics of the subjects: age,
height, weight, and BMI (Body Mass Index).
Age (yr) Height (cm) Weight (kg) BMI (kg/m
−2
)
mean 29.3 174 68.5 22.5
std 5.8 3.4 12.6 3.4
range 23–38 169–178 53–85 18–27
s drives the system nonlinearly, describing the non-
linear increase of the HR in response to the increase
in walking speed. It has been observed that there is a
curvilinear relationship between aerobic demand and
walking speed (see, e.g. (McArdle et al., 2007)).
2.1 Experimental Setup
The parameters in system (1) were identified from ex-
perimental data. The setup of the experiment is de-
scribed in this section.
Subject. Six healthy male subjects were studied.
The physical characteristics of the subjects are given
in Table 1.
Procedure. Each subject completed three exercise
sessions in separate occasions. In each session, a sub-
ject was requested to walk on a treadmill at a given
speed (5km/h, 6km/h, and 7km/h) for 15 minutes with
a recovery period of 15 minutes. After three sessions,
each subject completed the treadmill walking exercise
at the three different speeds.
Data Acquisition. In this study, the Powerjog fully
motorised medical grade treadmill was used. The HR
of the subjects was monitored by the wireless Polar
system and recorded by LabVIEW. The Polar sys-
tem generated pulses which were used to determine
the HR. To remove noises, the HR measurements
were then filtered using the moving average with a
5-second window.
Parameter Estimation. Using the measured HR
data and the Levenberg-Marquardt method, the pa-
rameters in system (1) were estimated for each sub-
ject and for the average response of all subjects .
Since there were three sets of input-output measure-
ments for each subject (where the input is the speed
of the treadmill and the output is the HR), we esti-
mated the parameters as if the following multi-input
multi-output system:
˙
x(t) = f(x(t),a, u(t)), y(t) = Cx(t), x(0) = 0
(2)
NONLINEAR MODELLING AND CONTROL OF HEART RATE RESPONSE TO TREADMILL WALKING
EXERCISE
499

where C =


1 0 0 0 0 0
0 0 1 0 0 0
0 0 0 0 1 0


, x =
[x
1
x
2
x
3
]
T
∈ R
6
, a = [a
1
a
2
...a
5
]
T
∈ R
5
,
u = [u
1
u
2
u
3
]
T
∈ R
3
and y = [y
1
y
2
y
3
]
T
∈ R
3
.
For i = 1,2, 3, the vector x
i
:= [x
i,1
x
i,2
]
T
and y
i
are
the state vector and the output from the input u
i
. The
unit of time t is in minute. To make the estimation
process more robust, the speeds of the treadmill
were normalised by 8 km/h, assuming the maximum
walking speed was 8 km/h. In other words, the
input vector u in (2) is in fact u = [5/8 6/8 7/8]
T
.
Similarly, the output y
i
(t) from the input u
i
(t) was
defined as y
i
(t) = (HR
i
(t) − 73.4)/60, where HR
i
(t)
is the absolute HR at time t, 73.4 bpm is the average
resting HR for all the subjects
2
, and 60 bpm is a
normalising factor.
The objective function was chosen as
S(a) =
N
∑
i=1
(y(t
i
) − ˆy(t
i
,a))
T
Q(y(t
i
) − ˆy(t
i
,a)) (3)
where, for i = 1,2,...,N, y(t
i
) is the measurement
of the output vector at time t
i
, ˆy(t
i
,a) is the output
of system (2) with the parameter vector a, and Q
is a given diagonal weighting matrix. In this study,
Q := diag([2.5 1.5 1]) was used. With the objec-
tive function (3), the Levenberg-Marquardt method
was used to determine an estimate of a which was
denoted as ˆa := [ ˆa
1
ˆa
2
... ˆa
5
]
T
(see, e.g. (Stortelder,
1996)). Based on a linear approximate method (see
e.g. (Stortelder, 1996)), an approximate 100(1− α)%
independent confidence interval for each estimate was
given by ( ˆa
i
− δa
i
, ˆa
i
+ δa
i
), for i = 1, 2,...,5. An α
level of 0.05 was used for obtaining the confidence
intervals of parameter estimates. Table 2 summaries
the estimated parameters for each subject and it also
shows the estimated parameters for the average re-
sponse from all the subjects. The simulated HR re-
sponses with the proposed model based on the aver-
age response are shown in Figure 1.
3 CONTROLLER DESIGN
In the second part of this paper, a controller design
is proposed for the regulation of HR. The controller
essentially controls the speed of the treadmill and in
turns controls the HR. It is desirable to design a con-
troller that is suitable for all the subjects, rather than
designing a controller for each individual subject. To
design such a controller, the model for the average
2
Resting HR was estimated from the 3-minute resting
period before exercise.
Table 2: Estimated parameter values for 6 different subjects
and the average response of all subjects.
Parameter estimates
(Confidence intervals, δa)
Subject ˆa
1
ˆa
2
ˆa
3
ˆa
4
ˆa
5
1 2.374 2.319 0.024 0.018 0.000
(0.180) (0.161) (0.014) (0.003) (0.308)
2 3.351 3.591 0.126 0.071 0.683
(0.334) (0.340) (0.008) (0.004) (0.009)
3 1.940 1.597 0.038 0.054 0.507
(0.180) (0.138) (0.007) (0.004) (0.010)
4 1.041 0.787 0.072 0.069 0.491
(0.078) (0.052) (0.011) (0.007) (0.015)
5 3.665 2.394 0.169 0.107 0.476
(0.489) (0.304) (0.023) (0.013) (0.029)
6 1.782 1.442 0.110 0.105 0.562
(0.166) (0.123) (0.009) (0.007) (0.013)
average 1.858 1.655 0.057 0.046 0.550
response (0.119) (0.099) (0.007) (0.003) (0.009)
0 5 10 15 20 25 30
60
80
100
Treadmill speed 5km/h
Time (min)
HR (BMP)
0 5 10 15 20 25 30
60
80
100
120
Treadmill speed 6km/h
Time (min)
HR (BMP)
0 5 10 15 20 25 30
60
80
100
120
140
Treadmill speed 7km/h
Time (min)
HR (BMP)
Figure 1: HR responses: actual responses from all subjects
(dots), average response (circles) and simulated response
(solid line).
response was utilised (see Table 2). Substituting the
parameters estimated from the average response, sys-
tem (1) is written in the state-space form as follows:
˙x = Ax+ B
1
φ(x
1
) + B
2
g(u), y = Cx
(4)
where
A =

−1.858 1.655
0 −0.057

, B
1
=

0
1

, B
2
=

1.655
0

,
x =

x
1
x
2

T
, C =

1 0

, g(u) := u
2
, φ(x
1
) :=
0.046x
1
1+exp

−15(x
1
−0.55)

.
System (4) is a nonlinear system with nonlinear-
ity φ(x
1
) and nonlinear control input g(u). To over-
come the control input nonlinearity, a transformed in-
put v = g(u) is defined. The function φ(x
1
) can be
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
500

approximated by a piecewise linear function
γ(x
1
) =
(
0 if x
1
≤ 0.418
0.090x
1
− 0.038 if x
1
> 0.418.
In fact, γ(x
1
) is obtained by linearising the function
φ(x
1
) at x
1
= 0 and 0.5. As a result, system (4) can
be approximated by a piecewise affine system (see
e.g. (Rantzer and Johansson, 2000)).
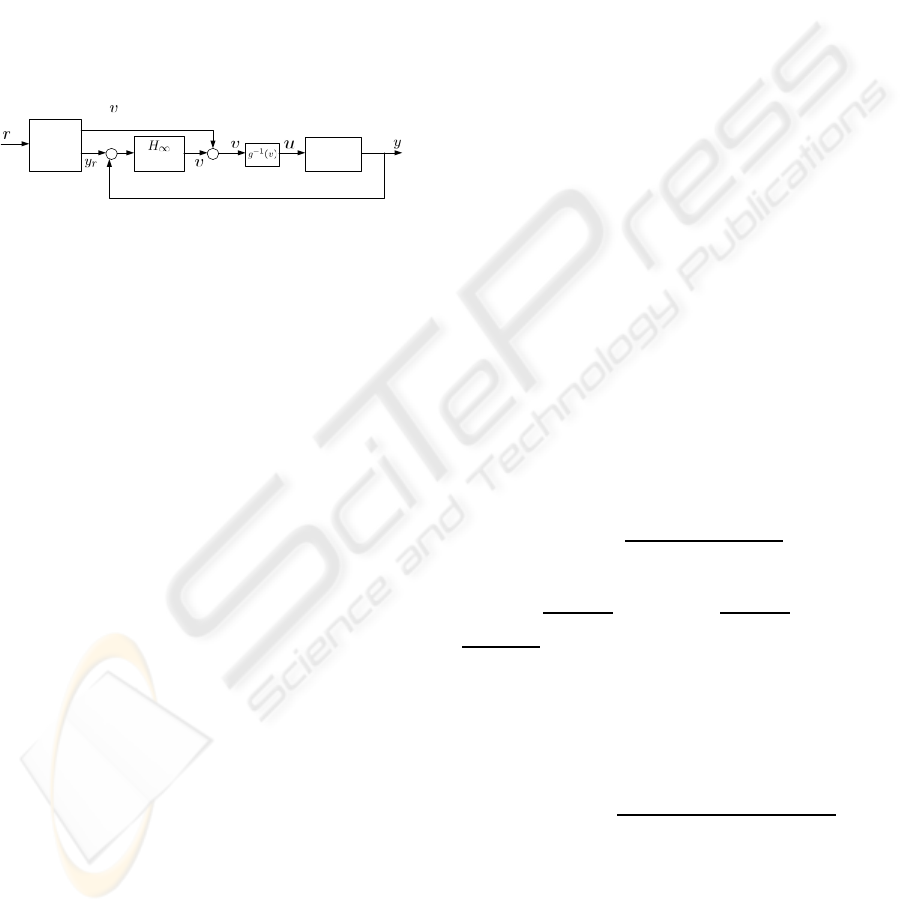
In this paper, we propose a two-degree-of-
freedom (2-DOF) controller consisting of a piecewise
linear quadratic (LQ) feedforward and a H
∞
feedback
controllers, as shown in Figure 2, for the control and
regulation of HR response.
Controller
Subject
Piecewise
LQ
+
+
+
-
feedforward
feedback
Figure 2: Control configuration.
3.1 LQ Feedforward Controller Design
First, we design the piecewise LQ feedforward con-
troller using the piecewise LQ optimal control tech-
nique (Rantzer and Johansson, 2000). We also incor-
porate an integral action in the controller.
Define two partitions of the state space:
X
1
:= {[x
1
x
2
]
T
∈ R
2


x
1
< 0.418}
X
2
:= {[x
1
x
2
]
T
∈ R
2


x
1
≥ 0.418}
Next, define
¯
A
i
=


A
i
0 a
i
−C 0 0
0
n×1
0 0


,
¯
B =


B
2
0
0


, ¯x =


x
e
1


for x ∈ X
i
and i = 1, 2, where
A
1
=

−1.858 1.655
0 −0.057

, A
2
=

−1.858 1.655
0.090 −0.057

,
a
1
=

0 0

T
, a
2
=

0 −0.038

T
, e(t) =
R
t
0
(r−
Cx(t))dt and r is the constant reference input. There-
fore, we have
˙
¯x =
¯
A
i
¯x+
¯
Bv, y =
¯
C¯x, for x ∈ X
i
. (5)
where
¯
C = [C 0 0]. Then, the control problem is
to find a control law v that minimises the follow-
ing cost function: J =
R
∞
0
( ¯x
T
¯
Q¯x + v
T
Rv)dt, for any
given
¯
Q ≥ 0 and R > 0. In the control design, the
matrix
¯
Q and the value of R were chosen as fol-
lows:
¯
Q = diag([0 0 10 0]), R = 0.5. By us-
ing the technique in (Rantzer and Johansson, 2000),
the minimising control law was v(t) = L
i
¯x,x ∈ X
i
,
i = 1,2, where L
1
=

−1.457 −0.989 4.471 0

,
L
2
=

−1.48 −1.001 4.471 0.009

. In turn, the
LQ feedforward controller is in the form:
˙
¯x =
¯
A
i
¯x+
¯
Bv+ B
r
r, y
r
=
¯
C¯x, v(t) = L
i
¯x,
(6)
for x ∈ X
i
where ¯x(0) = [0 0 0 1]
T
, B
r
= [0 0 1 0]
T
and
r is the reference input. In other words, the input to
this feedforward controller is the reference r and the
output are the feedforward control v and the “filtered”
reference y
r
.
3.2 H
∞
Controller Design
To cope with the uncertainty in the model, we design a
feedback controllerbased on the H
∞
control technique
(see e.g. (Petersen et al., 2000)). We first linearise the
system (4) and then formulate the control problem as
a mixed sensitivity problem (see e.g. (Skogestad and
Postlethwaite, 1996) for details). In a mixed sensi-
tivity problem, the idea is to choose some weighing
functions, namely W
1
(s), W
2
(s) and W
3
(s) to reflect
the control objectives. Generally, W
1
(s) is chosen to
meet a performance specification and W
3
(s) is cho-
sen to characterise the modelling errors. Whereas the
weighing function W
2
(s) may be used to reflect some
restrictions on the actuator signal.
In order to apply the mixed sensitivity technique,
the system (4) was linearised at x
0
= [0.5 0.13]
T
, v
0
=
0.43, and the transfer function of the linearised model
is given by
G(s) =
1.655s+ 0.094
s
2
+ 1.915s− 0.043
(7)
The weighting functions were then chosen as:
W
1
(s) =
0.02(s+5)
(s+0.0001)
, W
2
(s) =
700(s+0.3)
(s+2100)
, W
3
(s) =
100(s+7.13)
(s+800)
. By using MATLAB Robust Control Tool-
box, we obtained a controller K(s) that is fifth order,
resulting in a complicated control strategy. In fact, by
observing the Hankel singular values of the controller
K(s), a second order controller K
reduced
was in fact
adequate to approximate K(s) and it is in the form
K
reduced
(s) =
0.927s+ 0.009
s
2
+ 0.060s+ 6.008× 10
−6
(8)
4 SIMULATION RESULTS
As shown in Figure 2, a 2-DOF controller were
constructed by combining the LQ feedforward con-
trollers (6) and the H
∞
feedback controller (8). Since
both the feedforward and feedback controllers were
NONLINEAR MODELLING AND CONTROL OF HEART RATE RESPONSE TO TREADMILL WALKING
EXERCISE
501

0 2 4 6 8 10 12 14 16 18 20
80
90
100
110
120
130
Time (min)
HR (bpm)
Piecewise LQ + H inf
H inf
0 2 4 6 8 10 12 14 16 18 20
0
2
4
6
8
Time (min)
Speed (km/h)
Piecewise LQ + H inf
H inf
Figure 3: Subject 1–Simulation of HR regulation at 100
bpm and 120 bpm with H
∞
controller (dashed) and Piece-
wise LQ + H
∞
controller (solid).
obtained by considering the model of the average re-
sponse from the six subjects, it would be realistic to
validate the 2-DOF controller by applying it to each
of the subject without re-tuning the control parame-
ters for each subject. From the previous section, we
have a model for each of the subject and the estimated
parameters of the model are shown in Table 2.
We also assumed the treadmill speed was only al-
lowed to be operated between 0 and 8 km/h, since
speeds greater than 8 km/h may exceed the maximum
walking speed of some subjects. For each subject, we
tested the proposed controller by regulating the HRs
at 2 levels, namely 100 and 120 bpm. In the simu-
lations, the resting HR of each subject was assumed
to be the average of the three resting HRs, since each
subject performed 3 sets of walking exercise.
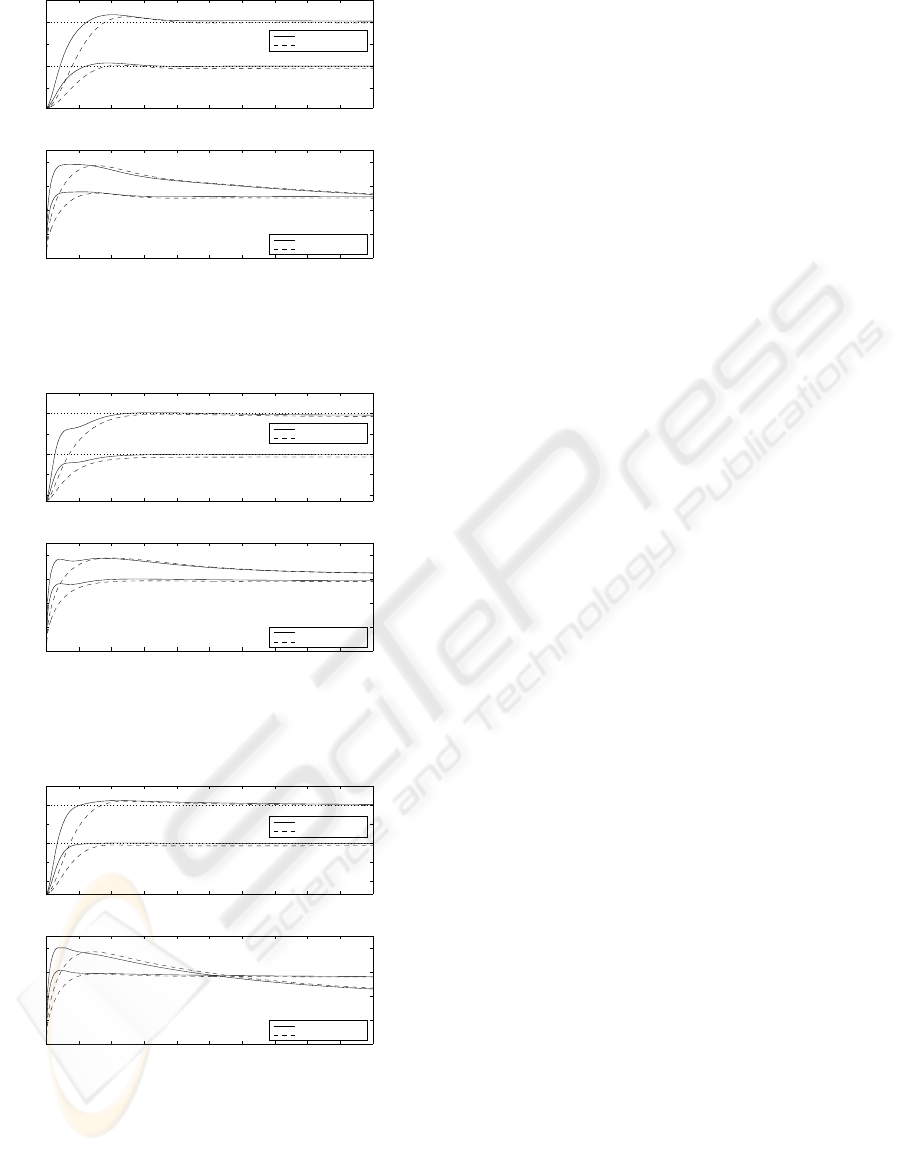
Figures 3–8 show the simulation results. Each fig-
ure shows the controlled HR responses and the speeds
of the treadmill. It also shows the responses from
the proposed 2-DOF controller and 1-DOF controller
which consists of H
∞
feedback controller only. For
each of the subject, the controlled HR was able to
track the reference HR signals. By comparing the re-
sponses from the 2-DOF controller and the H
∞
con-
troller, the proposed 2-DOF controller provides faster
responses. It indicates that the proposed 2-DOF con-
troller should give better performance than that of
only H
∞
controller.
5 CONCLUSIONS
In this study, a nonlinear model describing the HR re-
sponse to the treadmill walking exercise is proposed.
The proposed model is a feedback interconnected sys-
tem, consisting of a subsystem in the forward path
that can be used to describe the neural response, and a
0 2 4 6 8 10 12 14 16 18 20
60
70
80
90
100
110
120
130
Time (min)
HR (bpm)
Piecewise LQ + H inf
H inf
0 2 4 6 8 10 12 14 16 18 20
0
2
4
6
8
Time (min)
Speed (km/h)
Piecewise LQ + H inf
H inf
Figure 4: Subject 2–Simulation of HR regulation at 100
bpm and 120 bpm with H
∞
controller (dashed) and Piece-
wise LQ + H
∞
controller (solid).
0 2 4 6 8 10 12 14 16 18 20
80
90
100
110
120
130
Time (min)
HR (bpm)
Piecewise LQ + H inf
H inf
0 2 4 6 8 10 12 14 16 18 20
0
2
4
6
8
Time (min)
Speed (km/h)
Piecewise LQ + H inf
H inf
Figure 5: Subject 3–Simulation of HR regulation at 100
bpm and 120 bpm with H
∞
controller (dashed) and Piece-
wise LQ + H
∞
controller (solid).
feedback subsystem can be utilised to describe the pe-
ripheral local response. Utilising this model, a 2-DOF
controller was developed for the regulation of HR
for treadmill walking exercise. The controller con-
sists of a piecewise LQ feedforward and a H
∞
feed-
back controller. One of the benefits of introducing the
feedforward control is to improve the performance,
since robust control such as H
∞
controller is some-
times overly conservative that impedes performance.
The controller was derived from the model of average
response of the six participated subjects. Simulation
results showed that the proposed controller had the
ability to regulate HR for all the six subjects, without
the need to re-tune the controller’s parameters.
ACKNOWLEDGEMENTS
This work was supported by the Australian Research
Council.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
502

0 2 4 6 8 10 12 14 16 18 20
90
100
110
120
130
Time (min)
HR (bpm)
Piecewise LQ + H inf
H inf
0 2 4 6 8 10 12 14 16 18 20
0
2
4
6
8
Time (min)
Speed (km/h)
Piecewise LQ + H inf
H inf
Figure 6: Subject 4–Simulation of HR regulation at 100
bpm and 120 bpm with H
∞
controller (dashed) and Piece-
wise LQ + H
∞
controller (solid).
0 2 4 6 8 10 12 14 16 18 20
80
90
100
110
120
130
Time (min)
HR (bpm)
Piecewise LQ + H inf
H inf
0 2 4 6 8 10 12 14 16 18 20
0
2
4
6
8
Time (min)
Speed (km/h)
Piecewise LQ + H inf
H inf
Figure 7: Subject 5–Simulation of HR regulation at 100
bpm and 120 bpm with H
∞
controller (dashed) and Piece-
wise LQ + H
∞
controller (solid).
0 2 4 6 8 10 12 14 16 18 20
80
90
100
110
120
130
Time (min)
HR (bpm)
Piecewise LQ + H inf
H inf
0 2 4 6 8 10 12 14 16 18 20
0
2
4
6
8
Time (min)
Speed (km/h)
Piecewise LQ + H inf
H inf
Figure 8: Subject 6–Simulation of HR regulation at 100
bpm and 120 bpm with H
∞
controller (dashed) and Piece-
wise LQ + H
∞
controller (solid).
REFERENCES
Achten, J. and Jeukendrup, A. E. (2003). Heart rate mon-
itoring: Applications and limitations. Sports Med.,
33(7):517–538.
Brodan, V., Hajek, M., and Kuhn, E. (1971). An analog
model of pulse rate during physical load and recovery.
Physiologia Bohemoslovaca, 20:189–198.
Cole, C. R., Blackstone, E. H., F. J. Pashkow, C. E. S., and
Lauer, M. S. (1999). Heart rate recovery immediately
after exercise as a predictor of mortality. The New
England Journal of Medicine, 341(18):1351–1357.
Cooper, R. A., Fletcher, T. L., and Robertson, R. N. (1998).
Model reference adaptive control of heart rate during
wheelchair ergometry. IEEE Transactions on Control
Systems Technology, 6(4):507–514.
Coyle, E. F. and Alonso, G. (2001). Cardiovascular drift
during prolonged exercise: New perspectives. Exer-
cise and Sports Science Review, 29:88–92.
Hajek, M., Potucek, J., and Brodan, V. (1980). Mathemati-
cal model of heart rate regulation during exercise. Au-
tomatica, 16:191–195.
Kawada, T., Sunagawa, G., Takaki, H., Shishido, T.,
Miyano, H., Miyashita, H., Sato, T., Sugimachi, M.,
and Sunagawa, K. (1999). Development of a servo-
controller of heart rate using a treadmill. Japanese
Circulation Journal, 63:945–950.
McArdle, W. D., Katch, F. I., and Katch, V. L. (2007). Exer-
cise Physiology: Energy, Nutrition & Human Perfor-
mance. Lippincott Williams & Wilkins, Philadelphia,
PA, 6 edition.
Petersen, I. R., Ugrinovskii, V. A., and Savkin, A. V. (2000).
Robust Control Design Using H
∞
Methods. Springer-
Verlag, London.
Rantzer, A. and Johansson, M. (2000). Piecewise linear
quadratic optimal control. IEEE Transactions on Au-
tomatic Control, 45(4):629–637.
Rowell, L. B. (1993). Human Cardiovascular Control. Ox-
ford University Press, New York.
Savonen, K. P., Laka, T. A., Laukkanen, J. A., Halonen,
P. M., Rauramaa, T. H., Salonen, J. T., and Raura-
maa, R. (2006). Heart rate response during exercise
test and cardiovascular mortality in middle-aged men.
European Heart Journal, 27:582–588.
Skogestad, S. and Postlethwaite, I. (1996). Multivariable
Feedback Control. Wiley, England.
Stortelder, W. J. H. (1996). Parameter estimation in dy-
namic systems. Mathematics and Computers in Simu-
lation, 42:135–142.
Su, S. W., Wang, L., Celler, B. G., Savkin, A. V., and Guo,
Y. (2007). Identification and control for heart rate reg-
ulation during treadmill exercise. IEEE Transactions
on Biomedical Engineering, 54(7):1238–1246.
NONLINEAR MODELLING AND CONTROL OF HEART RATE RESPONSE TO TREADMILL WALKING
EXERCISE
503