BREAST CANCER DETECTION USING GENETIC

PROGRAMMING

Hong Guo, Qing Zhang and Asoke K. Nandi

Department of Electrical Engineering and Electronics

The University of Liverpool, Brownlow Hill, Liverpool, L69 3GJ, U.K.

Keywords:

Genetic Programming, Feature Extraction, Classiﬁcation, Breast Cancer Diagnosis.

Abstract:

Breast cancer diagnosis have been investigated by different machine learning methods. This paper proposes a

new method for breast cancer diagnosis using a single feature generated by Genetic Programming (GP). GP as

an evolutionary mechanism that provides a training structure to generate features. The presented approach is

experimentally compared with some kernel feature extraction methods: Kernel Principal Component Analysis

(KPCA) and Kernel Generalised Discriminant Analysis (KGDA). Results demonstrate the capability of the

proposed method to transform information from high dimensional feature space into one dimensional space

for breast cancer diagnosis.

1 INTRODUCTION

Breast Cancer is the second most common cancer in

the UK after non-melanoma skin cancer (Can). The

early detection of breast cancer is becoming very im-

portant to ameliorate breast cancer survival rate. In

recent years, various machine learning methods have

been proposed for breast cancer diagnosis and prog-

nosis. Yao and Liu described two neural network

based approaches to breast cancer diagnosis; a feed-

forward neural networks was evolved using evolu-

tionary programming algorithm in the ﬁrst approach,

while the second approach was based on neural net-

work ensembles (Yao and Liu, 1999). The perfor-

mance of four fuzzy rule generation methods on Wis-

consin breast cancer data was studied in (Jain and

Abraham, 2004). In (Kermani et al., 1995), a hy-

brid genetic algorithm and neural network (GANN)

was shown to extract the important features and train

a NN in breast cancer classiﬁcation. Guo and Nandi

developed a modiﬁed Fisher criterion to help genetic

programming optimism features for breast cancer di-

agnosis (Guo and Nandi, 2006). Nandi et al. used

GP successfully for classiﬁcation of breast masses in

mammogram (Nandi et al., 2006).

In recent years, the application of genetic pro-

gramming to pattern recognition problem has become

increasingly common. Genetic Programming was

ﬁrst introduced by Koza (Koza, 1992), and has been

proposed as a machine learning method in different

ﬁelds. In (Benyahia and Potvin, 1998), GP technique

was used to develop a decision support system for ve-

hicle dispatching considering a population of utility

functions that evaluate candidate vehicles for servic-

ing requests. GP was tested in six medical diagno-

sis problems (Brameier and Banzhaf, 2001) and the

results were compared with those obtained by neu-

ral networks. In (Kishore et al., 2000) the feasibility

of applying GP to multi-category pattern classiﬁca-

tion problem was studied. Zhang et al. (Zhang et al.,

2003) applied genetic programming for fault detec-

tion in machine condition monitoring ﬁeld. However,

in all the above applications (Benyahia and Potvin,

1998; Brameier and Banzhaf, 2001; Kishore et al.,

2000; Zhang et al., 2003), GP was employed solely

as a classiﬁer based on manually developed features.

In (Sherrah et al., 1997), GP-based feature extraction

was used to improve the classiﬁcation results and re-

duce the dimensionality of the data in the medical

domain. GP exhibits pseudo-intelligent behaviour by

deciding whether to perform feature extraction or fea-

ture selection during the evolutionary process. Unfor-

tunately, the system is unable to sample adequately

the search space for high-dimensional problems and

334

Guo H., Zhang Q. and K. Nandi A. (2008).

BREAST CANCER DETECTION USING GENETIC PROGRAMMING.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 334-341

DOI: 10.5220/0001059203340341

 SciTePress

the main disadvantage lies in its computational com-

plexity. Kotani et al. (Kotani et al., 1997) performed

feature extraction using GP with a KNN classiﬁer on

one artiﬁcial task and one acoustic diagnosis exper-

iment with the conclusion that the genetic program-

ming is an effective tool for the feature extraction

task.

In this paper, GP is employed to generate a single

nonlinear feature to improve the classiﬁcation accu-

racy for breast cancer diagnosis. As a machine learn-

ing method, GP exhibits intelligent behaviour to per-

form feature generation. During the evolutionary pro-

cess, a new ﬁtness function is developed to evaluate

the effectiveness of each feature in helping GP select

the best features by which the patterns from benign

are well separated from patterns from malignant.

This paper is organized as follows: The data

preparation of breast cancer is addressed in Section

2. Section 3 presents the proposed feature generator

using genetic programming. Two kernel feature ex-

traction methods kernel principal component analysis

(KPCA) and kernel generalized discriminant analy-

sis (KGDA) are brieﬂy presented in section 4. Three

classiﬁers Multi-Layer Prceptron (MLP), k-Nearest

Neighbor (KNN) and Minimum Distance Classiﬁer

(MDC) are presented in section 5. In section 6, a num-

ber of experiments for breast cancer detection prob-

lems are reported using kernel Principal Component

Analysis, kernel Generalized Discriminant Analysis

extracted features and GP generated feature. Finally,

based on the experimental results, conclusions on this

proposed method are presented in section 7.

2 THE PROBLEM

It is of prime importance to be able to detect the breast

cancer in early stages. In this paper, the Wisconsin

diagnostic breast cancer (WDBC) dataset from the

UCI Machine Learning repository (D.J. Newman and

Merz, 1998) is used to examine the capability of GP

for the breast cancer detection problem.

2.1 Image Preparation

The Wisconsin diagnostic breast cancer (WDBC)

dataset was created by Wolberg et al., University of

Wisconsin (Street et al., 1993). The diagnosis proce-

dure begins by obtaining a small drop of ﬂuid from

a breast tumour using a ﬁne needle. The image for

digital analysis is generated by JVC TK-1070 colour

video camera mounted atop an Olympus microscope

and the image is projected into the camera with a

63× objective and a 2.5× ocular. The image is cap-

tured by a ComputerEyes/RT colour frame grabber

board (Digital Vision, Inc., Dedham MA 02026) as

a 512× 480, 8-bit-per-pixel Targa ﬁle.

2.2 Data Preparation

An active model located in the actual boundary of cell

nucleus is deﬁned as a snake. The ten different fea-

tures from the snake-generated cell nuclei boundaries

are extracted by following techniques:

• Radius: The radius of an individual nucleus is

measured by averagingthe length of the radial line

segments deﬁned by the centroid of the snake and

the individual snake points.

• Perimeter: The nuclear perimeter is deﬁned by

calculating the total distance between the snake

points.

• Area: The nuclear area is deﬁned by counting the

number of pixels on the interior of the snake and

adding one-half of the pixels in the perimeter.

• Compactness: The perimeter

/area is used as

the compactness of the cell nuclei.

• Smoothness: The smoothness of a nuclear con-

tour is quantiﬁed by measuring of difference be-

tween the length of a radial line and the mean

length of the lines surrounding it.

• Concavity: Concavity is deﬁned as the severity of

indentations in a cell nucleus. For a line connect-

ing any two non-adjacent snake points, if the ac-

tual boundary drop inside the line, an indentation

occurs and the distance to the line is a measure of

the severity.

• Concave Points: This feature is similar to Con-

cavity but measures only the number, rather than

the magnitude, of contour concavities.

• Symmetry: The length difference between lines

perpendicular to the major axis to the cell bound-

ary in both directions is deﬁned as symmetry.

• Fractal Dimension: The fractural dimension is an

indication of the regularity of the nucleus. Higher

values of the downward slops of the coastlines

correspond to less regular contour and vice-versa.

• Texture: The texture of the cell nucleus is deﬁned

by ﬁnding the variance of the gray scale intensities

in the component pixels.

BREAST CANCER DETECTION USING GENETIC PROGRAMMING

335

TRoot

tanh

feature2

feature1

Figure 1: Tree Representation.

The mean value, largest value and standard error of

each feature are computed for each image. A set of

569 images has been processed, yielding a database of

30-dimensional points (Street et al., 1993). In this pa-

per, we randomly selected, without replacement, 100

samples for benign case, and 100 samples for malig-

nant case respectively. Two 30× 200 matrices are ob-

tained for training and test datasets. One of them as

the training dataset forms the terminator set to the GP.

Another matrix is used as the test dataset. For each

given pattern vector of training and test datasets, a

corresponding vector is created in a matrix contain-

ing the target information.

3 GENETIC

PROGRAMMING-BASED

FEATURE GENERATOR

In this paper, we introduce a new method for a feature

generator based on GP, for breast cancer detection

problem. Genetic Programming, as a form of evo-

lutionary algorithm and an extension of genetic algo-

rithms, extracts the information from the real-valued

parameter vector to create features based on the evo-

lutionary algorithm. The surviving feature from the

feature generator will be used to provide the solution

to pattern recognition problems.

3.1 The Representation of Each

Individual

Since expressions can be represented as trees or-

dered by operator precedence, GP systems in this pa-

per evolve programs using tree representation. Each

member can be written as a polynomial expression

consisting of several non-linear functions up to a max-

imum speciﬁed depth. Using this function, each in-

dividual in the population is a mathematical formula

that transforms the time series signals into a feature

data. Formula TRoot = tanh( feature1) + feature2

can be represented by the Fig. 1.

3.2 Process of Genetic Programming

The GP-based feature extractor is used to extract use-

ful information from the thirty features of breast can-

cer dataset in order to provide discriminating input

features for the classiﬁers. The purpose of GP is to try

to maximise the extra information content in the sam-

ple of the original feature set, and it implicitly max-

imises the separation between benign condition and

malignant condition within the data. The evolution-

ary process of GP-based feature generation system is

described by following steps. First, an initial popula-

tion with a chosen number of individuals is generated

on a random basis, meaning that there is no human in-

ﬂuence or bias in the generation of original features.

Original feature set are fed as the inputs to the ini-

tial population. Each individual represents a transfor-

mation network, which tries to transform dataset into

information for classiﬁcation.

In terms of the usefulness of each individual for

classiﬁcation, a ﬁtness value is assigned to each in-

dividual by ﬁtness function. The members with the

best ﬁtness values survive from the current genera-

tion and will be chosen as the origins of the next gen-

eration. In our design, only the elite will survive the

natural selection. This mechanism allows the feature

to evolve in a direction towards the best classiﬁcation

performance, thus achieving the automatic generation

of features. At the beginning of the next generation,

three operations - reproduction, crossover and muta-

tion - are conducted to produce new members based

on the surviving member. If the termination criterion

is met, the best solution is preserved.

3.3 Fitness Function

The ﬁtness function is one of the most important com-

ponents. It determines the performance of the GP sys-

tem. A good ﬁtness function provides an improved

solution by rating the performance of each member

and giving the stronger one a better chance of surviv-

ing. It is well known that the computational demands

are relatively high in training a classiﬁer for each in-

dividual when the classiﬁcation results are used as

the ﬁtness value for breast cancan diagnosis problem.

Hence in this study it is decided that classiﬁcation re-

sults are not used as a measure of ﬁtness. This deci-

sion reduces the computational complexity of the pro-

posed method signiﬁcantly

Within the one-dimensional effective feature

space, the achievable classiﬁcation success is de-

pendent upon the overlapping areas between classes.

Usually, a threshold is set within the area to sepa-

rate data belonging to different classes. However, it

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

336

Figure 2: Crossover operation

is inevitable that some data points are misclassiﬁed.

Apparently the smaller the overlapping area, by the

smaller number of data points within the overlapping

area, the higher is the classiﬁcation success. This rule

is explored in our ﬁtness function to reveal quickly

and effectively the discriminating ability of the candi-

date features. Speciﬁcally, the higher boundary of the

lower class and the lower boundary of the higher class

are calculated. The number of data points present

within these two boundaries are found out and then

normalised by the total number of data points. A

small percentage of the overlapping points is an in-

dication how well the two classes can be separated.

3.4 Primitive Operations

Genetic programming evolves tree individuals repre-

senting possible solutions to the problem at hand. A

population of such individuals is randomly created

and then evolved by probability of genetic operations:

• Crossover: GP carries out a crossover operation

to create new individuals with a probability P

which controls the occurrence of the crossover

throughout generations. Two new individuals

are generated by selecting compatible nodes ran-

domly from each parent and swapping them, as

illustrated in Fig. 2.

• Mutation: The mutation operation is performed

by the creation of a subtree at a randomly selected

node with the probability P

. First, for a given

parent, there is an index assigned to each node

for identiﬁcation. A random index number is gen-

erated to indicate the place where mutation will

happen. The node is located, then the tree down-

stream from this node is deleted and a new subtree

is generated from this node (see Fig. 3), exactly

in the same way as growing initial population.

• Reproduction: The reproduction operation is per-

formed by copying individuals to the next pop-

ulation without any change in terms of a certain

probability P

Figure 3: Mutation operation.

Table 1: The Operator sets for the GP.

Symbol No. of Inputs Description

+, - 2 Addition, Subtraction

*, / 2 Multiplication, Division

square, sqrt 1 Square, Square Root

sin, cos 1 Trigonometric functions

asin, acos 1 Trigonometric functions

tan, tanh 1 Trigonometric functions

reciprocal 1 Reciprocal

log 1 Natural Logarithm

abs, negator 1 Absolute, Change Sign

All these three operations happen within one gen-

eration based on three probabilities, such that:

+ P

= 1 (1)

3.5 Primitive Terminators

Terminators act as the interface between GP and the

experimental dataset. They are required to collect re-

lated information as much as possible from the orig-

inal feature set and to provide inputs to the feature

generator. In our GP-based feature extractor, the ter-

minator set is constructed by thirty original feature set

(see Section 2) and some numerical values, which are

randomly generated at the construction cycle of new

individuals. These numerical values could be either

integer or ﬂoating point numbers, both ranging from

1 to 100.

3.6 Primitive Operators

One of the main building blocks of the GP is the oper-

ator pool. The functions stored in the pool are math-

ematical operators that perform an operation on one

or more inputs to give an output result. Table 1 lists

the mathematical functions used as operators in this

paper.

BREAST CANCER DETECTION USING GENETIC PROGRAMMING

337

4 KERNEL FEATURE

EXTRACTION METHODS

In recent years, kernel-based methods are becoming

popular for their ability to solving nonlinear prob-

lems. It is ﬁrst applied to overcome the computational

and statistical difﬁcultly of SVM classiﬁer for seek-

ing an optimal separating hyperplane in the feature

space(E.Osuna et al., 1997). It is demonstrated to be

able to represent complicated nonlinear relationship

of the input data efﬁciently.

The Kernel Principal Component Analysis

(KPCA) and Kernel Generalised Discriminant

Analysis (KGDA) are two independent nonlinear

feature extraction/selection methods, both of which

perform the mapping in the feature space F with

kernel functions and use a linear analysis algorithm

to discover patterns in the kernel-deﬁned space.

The mapping function Φ is deﬁned implicitly by

specifying the form of the dot product in the feature

space (Scholkopf et al., 1998).

4.1 Kernel Principal Component

Analysis

Kernel PCA is the non-linear extension of the PCA in

a kernel-deﬁned feature space making use of the dual

representation (Shawe-Taylor and Cristianini, 2004).

Given a set of observations {~x

∈ R

: i = 1 to N},

we ﬁrst map the data into a feature space F and com-

pute the covariance matrix(Muller et al., 2001):

C =

∑

j=1

Φ(x

)Φ(x

)

(2)

The N × N Kernel Matrix is deﬁned as,

:= Φ(~x

) • Φ(~x

) = K(~x

,~x

); i, j = 1,...,N

(3)

The data need to be centred in the mapped feature

space F

≡

Φ(~x

) •

Φ(~x

) = K

−

∑

p=1

−

∑

q=1

∑

p,q=1

(4)

Now the eigenvalue problem for the expansion coef-

ﬁcients α

is solely dependent on the kernel function,

λα =

Kα (5)

Projects the mapped pattern Φ(x) onto V

to extract

features of new dataset x with kernel PCA.

· Φ(x)) =

∑

i=1

(Φ(x

) · Φ(x)) =

∑

i=1

K(x

,x)

(6)

4.2 Kernel Generalized Discriminant

Analysis (KGDA)

KGDA is derived from a linear version of the dis-

criminant analysis, namely, Fisher linear discriminant

analysis FLDA. FLDA is designed optimally with its

ability to maximise the ratio of within-class scatter

and between-class scatter of projected features. For

c (c > 2) classes, the ith observation vector from the

class l is deﬁned by x

, where 1 ≤ l ≤ c, 1 ≤ i ≤ N

and N

is the number of observationsfrom class l. The

within-class covariance matrix is given by

∑

l=1

, (7)

where

∑

i=1

− µ

)(x

− µ

)

(8)

The between-class covariance matrix is deﬁned by

∑

l=1

(µ

− µ)(µ

− µ)

(9)

where µ

is the mean of class l and µ is the global

mean.

The idea of KGDA is to solve the problem of

FLDA in a kernel feature space, thereby yielding a

nonlinear discriminant in the input space. In term

of the dot product, the optimisation problem for the

KGDA in the feature space can be written as

J(α) =

(10)

where

∑

l=1

− kk

] (11)

= K

−

∑

l=1

(12)

∑

l=1

i, j = 1,...,N

(13)

k =

∑

i=1

i, j = 1,...,N (14)

where k

is the mean vector of kernel matrix of class

l, k indicates the global mean vector of kernel matrix

of K

The projection of the test dataset x into the dis-

criminant is given by

W · Φ(x) =

∑

i=1

k(x

,x) (15)

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

338

5 CLASSIFIERS

Three classiﬁers - Artiﬁcial Neural Networks

(ANNs), K-Nearest Neighbour (KNN) and Minimum

Distance Classiﬁer (MDC) - are employed in this

paper to evaluate the discriminating ability of features

generated by GP and other kernel feature extraction

methods discussed previously.

The Multi-Layer Peceptron (MLP) is chosen here

as the structure of the network for its overall perfor-

mance over other conﬁgurations. The MLP used here

consists of one hidden layer varying between 1 and 14

neurons and one output layer, with the hidden layer

having a logistic activation function and the output

layer using a linear activation function. For training

procedure, the back propagation algorithm with adap-

tive learning and momentum is used. The network is

trained for 10000 epochs using each feature set.

KNN is a supervised learning algorithm to classify

a test object based on majority of K-nearest neighbor

category. Given that the version of K = 1 is often

rather successful (Ripley, 2004). 1-NN is used as the

classiﬁer to examine the performance of features in

this paper.

MDC is the simplest classiﬁcation criterion. Basi-

cally, the method ﬁnds centres of classes and mea-

sures distances between these centres and the test

data. The distance is deﬁned as a measure of similar-

ity so that the minimum distance indicates the max-

imum similarity. In this paper, Euclidean distance is

used to investigate the capability of any feature ex-

tracted by this approach.

6 EXPERIMENTAL RESULTS

6.1 Feature Generation Result

Fig. 4 is obtained for detection of breast cancer by

running GP-based feature extractor with population

size 100, maximum tree depth 10 and terminating af-

ter the number of generations reaches 5000. Fig. 4

shows the output of a single feature, generated from

the original feature set with 30 dimensions, for the

training dataset and test dataset respectively. There

are 200 examples in total from two conditions, with

100 examples in the benign case and 100 examples

in the malignant case. It is clear from Figure 4 that

the two conditions are perfectly separated from each

other at training dataset, and three examples misclas-

siﬁed in test dataset.

0 50 100 150 200

−1

−0.5

0.5

Training data

0 50 100 150 200

−1

−0.5

0.5

Test data

Figure 4: Output of a single feature, generated by GP from

the original feature set with 30 dimensional breast cancer

data, for the 200 examples in each of the training dataset

and test dataset respectively.

6.2 Classiﬁcation Results

A number of experiments were carried out to evalu-

ate the discriminating ability of features generated by

GP and other classical feature extraction methods in

term of classiﬁcation performance using MLP, 1-NN

and the simplest classiﬁer MDC respectively. Twenty

runs of GP has been conducted for generating fea-

tures. Also, ﬁfty MLP have conducted using original

features and feature extracted by KPCA, KGDA and

GP respectively.

Table 2 presents the comparison results of classiﬁ-

cation success rate using feature set extracted by dif-

ferent method as the inputs to MLP, 1-NN and MDC.

It can be seen that the best classiﬁcation accuracy is

achieved by MLP when thirty original features are

used as input. One KPCA feature achieved the best

94.5% when MDC is use as the classiﬁer. one KGDA

feature with MLP and MDC achieved the same clas-

siﬁcation results 93.5%. When a GP extracted fea-

ture is employed, the improvementis signiﬁcant com-

pared with other classical feature extraction methods.

Together with MLP, KNN and MDC, it performs the

best with success rate at 98.5% among all of pattern

recognition systems. From the best classiﬁcation ac-

curacy it can be seen that GP generated features are

more robust compared with other methods.

BREAST CANCER DETECTION USING GENETIC PROGRAMMING

339

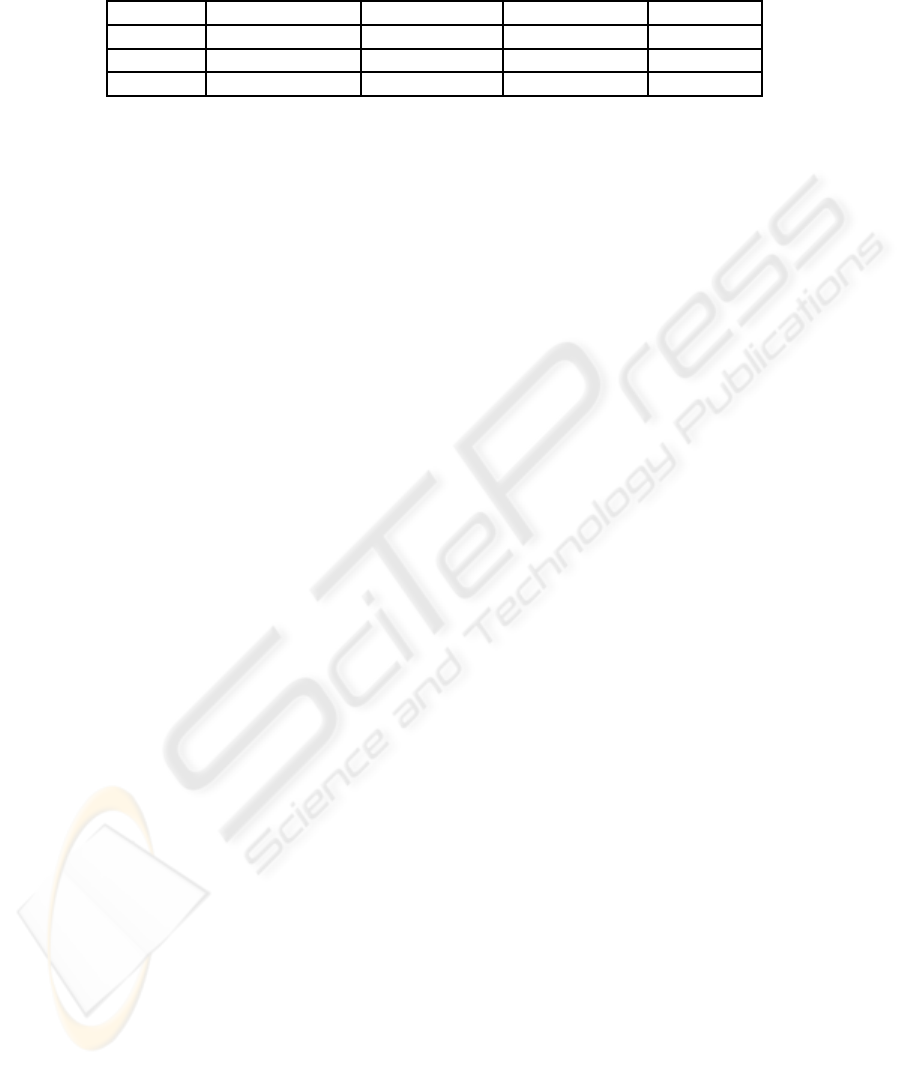
Table 2: The best classiﬁcation accuracy (%) using original features, one KPCA-extracted features, one KGDA-extracted

features and one GP-generated features respectively, with a MLP, a KNN and a MDC classiﬁer respectively on breast cancer

dataset.

Classiﬁer Original Feature KPCA Feature KGDA Feature GP Feature

MLP 97% 90% 93.5% 98.5%

KNN 87.5% 85.5% 93% 98.5%

MDC 84% 94.5% 93.5% 98.5%

7 CONCLUSIONS

It is now clear from Figure 4 that values of the single

feature obtained from our proposed method cluster

naturally into largely non-overlapping groups. Thus

no computationally complex classiﬁer may be needed

for successful classiﬁcation, instead some simple

thresholds are enough. Summarizing all the results

obtained from different approaches for breast cancer

diagnosis problem, it can be said that performances

from a single GP-generated feature are the most accu-

rate and reliable in all experiments. From the results

of different pattern recognition problems, GP is not

only capable of reducing the dimensionality, but also

achieving a signiﬁcant improvement in the classiﬁca-

tion accuracy. Using the single feature generated by

GP makes a signiﬁcant contribution to the improve-

ment in classiﬁcation accuracy and robustness, com-

pared with other sets of features extracted by KPCA

and KGDA.

Generally in pattern recognition problems, there is

a reliance on the classiﬁer to ﬁnd the discriminating

information from a large feature set in case of stand-

alone MLP. In this paper, GP as a machine learning

method is proposed for nonlinear feature extraction

for breast cancer diagnosis. This approach is able

to learn directly from the data just like conventional

methods (such as FLDA and PCA), but in an evolu-

tionary process. Under this framework, an effective

feature can be formed for pattern recognition prob-

lems without the knowledge of probabilistic distribu-

tion of data.

From the experimental results it can be seen that

with the combination of a simple form of classiﬁer

MDC, GP outperforms the other two feature extrac-

tors which are using more sophisticate classiﬁer MLP,

indicating an overwhelming advantage of GP in fea-

ture extraction for breast cancer diagnosis.

ACKNOWLEDGEMENTS

H. Guo would like to acknowledge the ﬁnancial sup-

port of the Overseas Research Studentship Commit-

tee, UK, the University of Liverpool and the Univer-

sity of Liverpool Graduates Association (HK)

REFERENCES

Cancer research UK.

Benyahia, I. and Potvin, J. (1998). Decision support for

vehicle dispatching using genetic programming. IEEE

Trans. Syst., Man, Cybern. Part.A, 28(3):306–314.

Brameier, M. and Banzhaf, W. (2001). A comparison of

linear genetic programming and neural networks in

medical data mining. IEEE Trans. on Evolutionary

Computation, 5(1):17–26.

D.J. Newman, S. Hettich, C. B. and Merz, C. (1998). UCI

repository of machine learning databases.

E.Osuna, Freund, R., and Girosi, F. (1997). Support Vec-

tor Machines: Training and Applications. MIT, Tech.

Rep.

Guo, H. and Nandi, A. K. (2006). Breast cancer diagnosis

using genetic programming generated feature. Pattern

Recognition, 39(5):980–987.

Jain, R. and Abraham, A. (2004). A comparative study

of fuzzy classiﬁcation methods on breast cancer data.

Australas. Physical Engineering Sciences Medicine,

27(4):213–218.

Kermani, B. G., White, M. W., and Nagle, H. T. (1995).

feature extraction by genetic algorithms for nerual net-

works in breast cancer classiﬁcation. volume 1, pages

831–832. New York, USA.

Kishore, J. K., Patnaik, L. M., Mani, V., and Arawal, V. K.

(2000). Application of genetic programming for mul-

ticategory pattern classiﬁcation. IEEE Trans. on Evo-

lutionary Computation, 4(3):242–258.

Kotani, M., Ozawa, S., Nasak, M., and K.Akazawa (1997).

Emergence of feature extraction function using ge-

netic programming. In Knowledge-Based Intelligent

Information Engineering Systems, Third International

Conference, pages 149–152.

Koza, J. R. (1992). Genetic Programming: On the Pro-

gramming of Computers by Means of Natural Selec-

tion. MIT Press, Cambridge.

Muller, K. R., Mika, S., Ratsch, G., Tsuda, K., and

Scholkopf, B. (2001). An introduction to kernel-based

learning algorithms. IEEE Trans. on Neural Networks,

12(2):181–201.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

340

Nandi, R. J., Nandi, A. K., Rangayyan, R. M., and Scutt,

D. (2006). Classiﬁcation of breast masses in mammo-

grams using genetic programming and feature selec-

tion. Medical and Biological Emgineering and Com-

puting, 44(8):693–694.

Ripley, B. D. (2004). Pattern Recognition and Neural Net-

works. Cambridge Universith Press, Boston.

Scholkopf, B., Smola, A., and Muller, K. R. (1998). Non-

linear component analysis as a kernel eigenvalue prob-

lem. Neural Computation, 10(5):1299–1319.

Shawe-Taylor, J. and Cristianini, N. (2004). Kernel Meth-

ods for Pattern Analysis. Cambridge University Press.

Sherrah, J. R., Bogner, R. E., and Bouzerdoum, A. (1997).

The evolutionary pre-processor: Automatic feature

extraction for supervised classiﬁcation using genetic

programming. In Proc. 2nd Int. Conf. Genetic Pro-

gramming (GP-97), pages 304–312.

Street, W., Wolberg, W., and Mangasarian, O. (1993). Nu-

clear feature extraction for breast tumor diagnosis. In

International Symposium on Electronic Imaging: Sci-

ence and Technology, number 1905, pages 861–870.

San Jose, CA.

Yao, X. and Liu, Y. (1999). Neural networks for breast can-

cer diagnosis. volume 3, pages 6–9.

Zhang, L., Jack, L. B., and Nandi, A. K. (2003). Fault detec-

tion using genetic progamming. Mechanical Systems

Signal Processing.

BREAST CANCER DETECTION USING GENETIC PROGRAMMING

341