AN EFFICIENT METHOD FOR VESSEL WIDTH MEASUREMENT

ON COLOR RETINAL IMAGES

Alauddin Bhuiyan, Baikunth Nath, Joselito Chua and Kotagiri Ramamohanarao

Department of Computer Science and Software Engineering and NICTA Victoria Research Laboratory

The University of Melbourne, Australia

Keywords:

Microvascular Sign, Gradient Operator, Adaptive Region Growing Technique, Texture Classiﬁcation, Gabor

Energy Filter Bank, Fuzzy C-Means Clustering.

Abstract:

Vessel diameter is an important factor for indicating retinal microvascular signs. In automated retinal image

analysis, the measurement of vascular width is a complicated process as most of the vessels are few pixels

wide. In this paper, we propose a new technique to measure the retinal blood vessel diameter which can be

used to detect arteriolar narrowing, arteriovenous (AV) nicking, branching coefﬁcients, etc. to diagnose related

diseases. First, we apply the Adaptive Region Growing (ARG) segmentation technique to obtain the edges

of the blood vessels. Following that we apply the unsupervised texture classiﬁcation method to segment the

blood vessels from where we obtain the vessel centreline. Then we utilize the edge image and vessel centreline

image to obtain the potential pixels pairs which pass through a centreline pixel. We apply a rotational invariant

mask to search the pixel pairs from the edge image. From those pixels we calculate the shortest distance pair

which will be the vessel width for that cross-section. We evaluate our technique with manually measured

width for different vessels’ cross-sectional area and achieve an average accuracy of 95.8%.

1 INTRODUCTION

Accurate measurement of retinal vessel diameter is

an important part in the diagnosis of many diseases.

A variety of morphological changes occur to retinal

vessels in different disease conditions. The change

in width of retinal vessels within the fundus image is

believed to be indicative of the risk level of diabetic

retinopathy; venous beading (unusual variations in di-

ameter along a vein) is one of the most powerful pre-

dictor of proliferate diabetic retinopathy. Generalized

and focal retinal arteriolar narrowing and arteriove-

nous nicking have been shown to be strongly associ-

ated with current and past hypertension reﬂecting the

transient and persistent structural effects of elevated

blood pressure on the retinal vascular network. In

addition, retinal arteriolar bifurcation diameter expo-

nents have been shown to change signiﬁcantly in pa-

tients with peripheral vascular disease and arterioscle-

rosis and a variety of retinal microvascular abnormal-

ities have been shown to relate to the risk of stroke

(Lowell et al., 2004). Therefore, an accurate measure-

ment of vessel diameter and geometry is necessary for

effective diagnosis of such diseases.

The measurement of the vascular diameter is crit-

ical and a challenging task whose accuracy depends

on the accuracy of the segmentation method. A re-

view for the blood vessel segmentation is provided in

the literature (Bhuiyan et al., 2007a). The study of

vessel diameter measurement is still an open area for

improvement. Zhou et al. (Zhou et al., 1994) have

applied a model-based approach for tracking and to

estimating widths of retinal vessels. Their model as-

sumes that image intensity as a function of distance

across the vessel displays a single Gaussian form.

However, high resolution fundus photographs often

display a central light reﬂex (Brinchman-hansan and

Heier, 1986). Intensity distribution curves is not al-

ways of single Gaussian form, so that using a sin-

gle Gaussian model for simulating intensity proﬁle

of vessel could produce poor ﬁts and subsequently

provide inaccurate diameter estimations (Gao et al.,

2001). Gao et al. (Gao et al., 2001) model the in-

tensity proﬁles over vessel cross section using twin

Gaussian functions to acquire vessel width. This tech-

nique may produce poor results in case of minor ves-

sels where the contrast is less. Lowell et al. (Low-

ell et al., 2004) have proposed an algorithm based on

ﬁtting a local 2D vessel model, which can measure

vascular width to an accuracy of about one third of

178

Bhuiyan A., Nath B., Chua J. and Ramamohanarao K. (2008).

AN EFFICIENT METHOD FOR VESSEL WIDTH MEASUREMENT ON COLOR RETINAL IMAGES.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 178-185

DOI: 10.5220/0001059401780185

 SciTePress

a pixel. However, the technique is biased on smooth

data (image) and suffers from measuring the width of

minor vessels where the contrast is very less.

In this paper, we introduce a new algorithm, based

on vessel centreline and edges information. We ap-

ply the adaptive region growing technique to segment

the vessels edges (Bhuiyan et al., 2007a) and the un-

supervised texture classiﬁcation method to segment

the vessels and detect the centreline (Bhuiyan et al.,

2007b). For each selected centerline pixel we map the

edge image of the retinal vessels edge pixels and ﬁnd

all the potential line end points or pairing pixels on

opposite edge passing through this centreline pixels.

From these potential lines we ﬁnd the line that has the

minimum length and consider this as the vessel width

for that cross-sectional area. In this way, we can mea-

sure the width of the blood vessel continuing through

the centreline of all the vessels. A speciﬁc feature of

our technique is that it can calculate the vessel width

when it is one pixel wide.

The rest of the paper is organized as follows: Sec-

tion 2 introduces the proposed method of blood ves-

sel width measurement. Edge based blood vessel seg-

mentation technique is described in section 3. Section

4 illustrates the vessel centreline detection procedure.

The vessel width measurement method is described

in section 5. The experimental results are provided

in section 6 and ﬁnally the conclusion and future re-

search directions are drawn in section 7

2 PROPOSED METHOD

We propose the blood vessels’ width measurement al-

gorithm based on the vessel edge and centreline. The

major advantage of our technique is that it is less sen-

sitive to noise and work equally for the low contrast

vessels (particularly for minor vessels). We adopt two

segmented images that are produced from the original

RGB image. At ﬁrst, we apply the ARG segmenta-

tion technique to obtain the vessel edges, then we ap-

ply the unsupervised texture classiﬁcation method to

segment the blood vessels from where we obtain the

vessel centreline. We map the vessel centreline image

and pick any of the vessel centreline pixel. For that

particular pixel we apply a rotational invariant mask

whose centre is that pixels position and searches the

potential pixels from the edge image using a contin-

uous increment of lower to higher distance and ori-

entation. For each case, if the gray scale value of that

pixel position is 255 or white it ﬁnds the mirror of this

pixel by searching through a ﬁxed angle (exactly in-

crementing 180 degree) but in variable distance. This

is to give the ﬂexibility and consistency to our method

as the centreline pixels may not be in the exact posi-

tion of vessel centre. In this way, we can obtain all the

potential pairs (line end points) which pass through

that centreline pixel. From those pairs we calculate

the minimum distance/length pair which is the width

of that cross-section of the blood vessel. Figure 1 de-

picts the overall technique of our proposed method.

Figure 1: The overall system for measuring blood vessel

width.

3 VESSEL EDGE DETECTION

We implemented the vessel segmentation technique

based on vessel edges. In the following subsections

we provide a brief illustration of this method.

3.1 Preprocessing of Retinal Image

Adaptive Histogram Equalization (AHE) method is

implemented, using MATLAB, to enhance the con-

trast of the image intensity by transforming the val-

ues using contrast-limited adaptive histogram equal-

ization (Figure 2).

3.2 Image Conversion

The enhanced retinal image is converted into gradient

image (Figure 2) using ﬁrst order partial differential

operator. The gradient of an image f(x,y) at location

(x,y) is deﬁned as the two dimensional vector (Gon-

AN EFFICIENT METHOD FOR VESSEL WIDTH MEASUREMENT ON COLOR RETINAL IMAGES

179

zalez and Wintz 1987)

G[ f(x, y)] = [G

] =



∂f

∂x

∂f

∂y



(1)

For edge detection, we are interested in the magni-

tude G[ f(x,y)] and direction α(x,y)of the vector, gen-

erally referred to simply as the gradient and denoted

and commonly takes the value of

G[ f(x, y)] ≈ |G

| + |G

α(x,y) = tan

−1

)

(2)

where the angle is measured with respect to the x axis.

Figure 2: Original retinal image, its Adaptive Histogram

Equalized image (top; left to right), the Gradient Image and

ﬁnal ARG output image (bottom; left to right).

3.3 Adaptive Region Growing

Technique

The edges of vessels are segmented using region

growing procedure(Gonzalez et al., 2004) that groups

pixels or sub regions into larger regions based on gra-

dient magnitude. As the gradient magnitude is not

constant for the whole vessel we need to consider an

adaptive gradient value that gradually increases or de-

creases to append the pixel to a region. We call it an

adaptive procedure, as the difference of neighboring

pixels intensity value is always adapted for the region

growing process. The region growing process starts

with appending the pixels that pass certain threshold

value. For region growing we ﬁnd the intensity dif-

ference between a pixel belonging to a region and

its neighboring potential region growing pixels. The

pixel is considered for appending in that region if the

difference is less than a threshold value. The thresh-

old value is calculated by considering the maximum

differential gradient magnitude for any neighboring

pixels with equal (approximately) gradient direction.

Region growing should stop when no more pixels sat-

isfy the criteria for inclusion in that region. In the

region growing process each region is labeled with a

unique number. For that purpose we construct a cell

array with region number and its pixel position. The

image is scanned in a row-wise manner until its end,

and each pixel that satisﬁes our criteria is taken into

account for growing a region with its 8-neighborhood

connectivity.

3.4 Parallel Region Detection

We calculate the parallel edges (regions) by consid-

ering pixel orientation belonging to each region. At

ﬁrst, we pick the region number and belonging pixel

coordinates from the constructed cell array. Then we

grouped the region/regions parallel to each region,

which is calculated by mapping the pixels gradient

direction. For each region every pixel is searched

from its potential parallel region and once a maximum

number of pixels match with the other region we con-

sider it as parallel to that region. We consider all re-

gions and once a region is considered we assigned a

ﬂag value to that region so that it will not be consid-

ered again. In this way we can only ﬁlter the vessels

from the region and discard all other regions, which

are background noise or other objects like haemor-

rhage, macula, etc in the retinal image.

3.5 Experimental Results

We considered DRIVE database (DRIVE-database,

2004) and applied our technique on ﬁve images for

initial assessment. For performance evaluation we

employed an expert to ﬁnd the number of vessels in

the original image and detected output image (Figure

2). We achieved an overall 94.98% detection accu-

racy.

4 VESSEL CENTRELINE

DETECTION

We implemented the unsupervised texture classiﬁca-

tion based vessel segmentation method from which

we detect the vessel centreline. We consider Gaus-

sian and L

∗

perceptually uniform color spaces

with the original RGB image for texture feature ex-

traction. To extract features, a bank of Gabor energy

ﬁlters with three wavelengths and twenty-four orien-

tations is applied in each selected color channel. Then

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

180

a texture image is constructed from the maximum re-

sponse of all orientations for a particular wavelength

in each color channel. From the texture images, a fea-

ture vector is constructed for each pixel. These fea-

ture vectors are classiﬁed using the Fuzzy C-Means

(FCM) clustering algorithm. Finally, we segment the

image based on the cluster centroid value.

4.1 Color Space Transformation and

Preprocessing

Generally image data is given in RGB space (because

of the availability of data produced by the camera

apparatus). The deﬁnition of L

∗

is based on an

intermediate system, known as the CIE XYZ space

(ITU-Rec 709). This space is derived from RGB as

below (Wyszecki and Stiles, 1982)

X = 0.412453R + 0.357580G+ 0.180423B

Y = 0.212671R+ 0.715160G+ 0.072169B

Z = 0.019334R+ 0.119193G+ 0.950227B

(3)

∗

color space is deﬁned as follows:

∗

= 116f(Y/Y

) − 16

∗

= 500[ f(X/X

) − f(Y/Y

)]

∗

= 200[ f(Y/Y

)] − f(Z/Z

)

(4)

where f(q) = q

1/3

if q < 0.008856 and is constant

7.87+16/116 otherwise. X

, Y

and Z

represent a

reference white as deﬁned by a CIE standard illumi-

nant, D

in this case. This is obtained by setting

R = G = B = 100 in (1), q ∈ {X/X

,Y/Y

,Z/Z

Gaussian color model can also be well approxi-

mated by the RGB values. The ﬁrst three components

and

λλ

of the Gaussian color model (Taylor

expansion of the Gaussian weighted spectral energy

distribution at Gaussian central wavelength and scale)

can be approximated from the CIE 1964 XYZ ba-

sis when taking λ

= 520nm (Gaussian central wave-

length) and σ

= 55nm (scale) as follows (Geuse-

broek et al., 2001)





λλ









−0.48 1.2 0.28

0.48 −0.4 −0.4

1.18 −1.3 0













(5)

The product of (3) and (5) gives the desired imple-

mentation of the Gaussian color model in RGB terms

(Figure 3). The Adaptive Histogram Equalization

method was implemented, using MATLAB, to en-

hance the contrast of the image intensity.

4.2 Texture Feature Extraction

Texture generally describes second order property of

surfaces and scenes, measured over image intensities.

Figure 3: Original RGB and its Green channel image (top;

left to right), Gaussian transformed ﬁrst and second compo-

nent image (bottom; left to right).

A Gabor ﬁlter has weak responses along all orien-

tations on the smooth (background) surface. On the

other hand, when it positioned on a linear pattern ob-

ject (like a vessel) the Gabor ﬁlter produces relatively

large differences in its responses when the orientation

parameter changes (Wu et al., 2006). Hence, the use

of Gabor ﬁlters to analyze the texture of the retinal

images is very promising. In the following two sub-

sections we illustrate the Gabor ﬁlter based texture

analysis method.

4.2.1 Gabor Filter

An input image I(x,y), (x,y) ∈ Ω where Ω is the set of

image points, is convolved with a 2D Gabor function

g(x,y), (x,y) ∈ ω, to obtain a Gabor feature image

r(x, y) (Gabor ﬁlter response) as follows (Kruizinga

and Petkov, 1999)

r(x, y) =

Ω

I(ξ, η)g(x− ξ,y− η)dξdη (6)

We use the following family of 2D Gabor functions to

model the spatial summation properties of an image

(Kruizinga and Petkov, 1999)

ξ,η,λ,Θ,φ

(x,y) = exp(−

′2

+γ

′2

2σ

)cos(2π

′

+ φ)

′

= (x− ξ) cosΘ− (y− η)sinΘ

′

= (x− ξ) cosΘ− (y− η)sinΘ

(7)

where the arguments x and y specify the position of

a light impulse in the visual ﬁeld and ξ,η,σ,γ, λ,Θ,φ

are parameters. The pair (ξ,η) speciﬁes the center of

a receptive ﬁeld in image coordinates. The standard

AN EFFICIENT METHOD FOR VESSEL WIDTH MEASUREMENT ON COLOR RETINAL IMAGES

181

deviation σ of the Gaussian factor determines the size

of the receptive ﬁled. Its eccentricity is determined by

the parameter γ called the spatial aspect ratio. The pa-

rameter λ is the wavelength of the cosine factor which

determines the preferred spatial frequency

of the

receptive ﬁeld function g

ξ,η,λ,Θ,φ

(x,y). The parame-

ter Θ speciﬁes the orientation of the normal to the

parallel excitatory and inhibitory stripe zones - this

normal is the axis x

′

in (5). Finally, the parameter

φ ∈ (−π,π), which is a phase offset argument of the

harmonic factor cos(2π

′

+ φ), determines the sym-

metry of the function g

ξ,η,λ,Θ,φ

(x,y).

4.2.2 Gabor Energy Features

A set of textures was obtained based on the use of

Gabor ﬁlters (6) according to a multichannel ﬁlter-

ing scheme. For this purpose, each image was ﬁltered

with a set of Gabor ﬁlters with different preferred ori-

entation, spatial frequencies and phases. The ﬁlter re-

sults of the phase pairs were combined, yielding the

Gabor energy quantity (Kruizinga and Petkov, 1999):

ξ,η,Θ,λ

ξ,η,Θ,λ,0

+ r

ξ,η,Θ,λ,π/2

(8)

where r

ξ,η,Θ,λ,0

and r

ξ,η,Θ,λ,π/2

are the outputs of the

symmetric and antisymmetric ﬁlters. We used Gabor

energy ﬁlters with twenty-four equidistant preferred

orientations(Θ = 0,15,30, ..,345) and three preferred

spatial frequencies (λ = 6,7,8). In this way an ap-

propriate coverage was performed of the spatial fre-

quency domain.

We considered the maximum response value per

pixel on each color channel to reduce the feature vec-

tor length and complexity of training on data for the

classiﬁer. In addition, we constructed an image (Fig-

ure 4) on each color channel which was used for

histogram analysis to determine the cluster number.

From these images we constructed twelve element

length feature vector for each pixel in each retinal im-

age to classify them into vessel and non-vessel using

the FCM clustering algorithm.

Figure 4: Texture analyzed image with the orientations of

15, 45 degrees and maximum response of all twenty-four

orientations (left to right).

4.3 Texture Classiﬁcation and Image

Segmentation

The FCM is a data clustering technique where in each

data point belongs to a cluster to some degree that is

speciﬁed by a membership grade. Let X = x

,,x

where x ∈ R

present a given set of feature data. The

objective of the FCM clustering algorithm is to mini-

mize the Fuzzy C-Means cost function formulated as

(Bezdek, 1981)

J(U,V) =

∑

j=1

∑

i=1

(µ

)

||x

− v

(9)

V = {v

,,v

} are the cluster centers. U = (µ

)

N×C

is fuzzy partition matrix, in which each member is be-

tween the data vector x

and the cluster j. The values

of matrix U should satisfy the following conditions:

∈ [0,1], i = 1, ..,N, j = 1, ..,C (10)

= 1,i = 1,.., N (11)

The exponent m ∈ [1,∞] is the weighting exponent,

which determines the fuzziness of the clusters. The

most commonly used distance norm is the Euclidean

distance d

= ||x

− v

||.

We used the Matlab Fuzzy Logic Toolbox for clus-

tering 253440 vectors (the size of the retinal image is

512x495) in length twelve for each retinal image. In

each retinal image clustering procedure, the number

of clusters was assigned after analyzing the histogram

of the texture image. The parameter values used for

the FCM clustering were as follows. The exponent

value of 2 for the partition matrix, maximum number

of iterations was set to 1000 for the stopping crite-

rion and the minimum amount of improvement be-

ing 0.00001. We received the membership values on

each cluster for every vector, from which we picked

the cluster number that belonged to the highest mem-

bership value for each vector and converted it into a

2D matrix. From this matrix we produced the binary

image considering the cluster central intensity value

which identiﬁes the blood vessels only.

4.4 Experimental Results

Using the DRIVE database (DRIVE-database, 2004)

we applied our method on ﬁve images for vessel seg-

mentation. For performance evaluation, we detected

the vessel centerline in our output segmented im-

ages and hand-labeled ground truth segmented (GT)

images applying the morphological thinning opera-

tion (Figure 5). We achieved an overall 84.37%

sensitivity (TP/(TP + FN)) and 99.61% speciﬁcity

(TN/(TN + FP)) where TP, TN, FP and FN are true

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

182

positive, true negative, false positive and false nega-

tive respectively. Hoover et al. (Hoover et al., 2000)

method on the same ﬁve segmented images provided

in 68.23% sensitivity and 98.06% speciﬁcity. Clearly,

our method produces superior results.

Figure 5: Original RGB image, vessel segmented image,

and its centreline image (from left to right).

5 VESSEL WIDTH

MEASUREMENT

After obtaining the vessels edge image and centre-

line image, we mapped these images to ﬁnd the vessel

width for a particular vessel centreline pixel position.

To do this we ﬁrst pick a pixel from the vessel cen-

treline image, then we apply a mask considering this

centreline pixel as its centre. The purpose of this mask

is to ﬁnd the potential edge pixels (which may fall in

width or cross section of the vessels) in any side of

that centreline pixel position. Therefore, we will ap-

ply the mask to the edge image only. For searching all

the pixel positions inside the mask, we calculate the

pixel position by shifting by one up to the size of the

mask and rotating each position from 0 to 180 degrees

at the same time. For increasing the rotation angle we

use the step size (depending on the size of the mask)

less then 180/(mask length). Therefore, we can access

every cell in the mask using this angle.

For each obtained position we search the edge im-

age gray scale value to check whether it is an edge

pixel or not. Once we ﬁnd an edge pixel we then ﬁnd

it’s mirror by shifting the angle of 180 degree and in-

creasing the distance from one to the maximum size

of the mask (Figure 6). In this way we produce a ro-

tational invariant mask and pick all the potential pixel

pairs to ﬁnd the width or diameter of that cross sec-

tional area.

x1 = x

′

+ r∗ cosθ

y1 = y

′

+ r∗ sinθ

(12)

where (x

′

) is the vessel centreline pixel position,

r=1,2,..(mask size)/2 and θ = 0, ..,180

. For any pixel

position, if the gray scale value in the edge image

is 255 (white or edge pixel) then we ﬁnd the pixel

(x2,y2) in the opposite edge (mirror of this pixel) con-

sidering θ = (θ+ 180) and varying r.

After applying this operation we obtain the pairs

of pixels which are on the opposite edges (at line

end points) giving imaginary lines passing through

the centerline pixels (Figure 6). From these pix-

els pairs we ﬁnd the minimum Euclidian distance

− x

)

+ (y

− y

)

, the width of that crosssec-

tion. In this way, we can measure the width for all

vessels including the vessels’ with one pixel wide (for

which we have the edge and the centreline itself).

Figure 6: Finding the mirror of an edge pixel(left) and width

or minimum distance from potential pairs of pixels (right).

6 EXPERIMENTAL RESULTS

AND DISCUSSION

We used the centreline images and edge images for

measuring the width of the blood vessels. We mea-

sure the accuracy qualitatively by comparing with the

width measured by plotting the centreline pixel and

its surround edge pixels. We considered ten different

vessel cross-sections of these images and observed

that our method is working very accurately. Figure

7 portrays the Grid for a cross-section of a blood ves-

sel where c is the centreline pixel and w1 to w8 are

potential width end points. Figure 8 depicts the de-

tected width for some cross-sectional points indicat-

ing in white lines (enlarged).

Figure 7: Grid showing the potential width edge pairs for a

cross-section with centreline pixel C.

For quantitative evaluation we considered ten

images (each 3072×2048 which captured with the

AN EFFICIENT METHOD FOR VESSEL WIDTH MEASUREMENT ON COLOR RETINAL IMAGES

183

Table 1: Measuring the accuracy of the automatic width measurement.

Cross- Centreline pixel Detected width end points Auto. width Accuracy Error

section X

(A) (%) (%)

1 2055 629 2068 632 2046 628 22.361 99.14 0.86

2 1859 519 1871 519 1850 520 21.024 97.50 2.50

3 2259 815 2259 811 2259 824 13 99.46 0.54

4 2350 1077 2350 1070 2350 1084 14 87.61 12.39

5 2233 1317 2239 1314 2239 1322 11.314 93.49 6.51

6 2180 1435 2189 1431 2172 1440 19.235 95.39 4.61

7 2045 1451 2055 1452 2042 1452 13 85.55 14.45

8 1683 1500 1691 1509 1680 1496 17.029 87.52 12.48

9 1579 617 608 1593 630 1573 23.409 98.48 1.52

10 1434 855 853 1436 859 1432 7.211 85.48 14.52

11 1443 1000 999 1446 1004 1440 7.81025 91.23 8.77

12 1618 1331 1335 1623 1330 1617 7.81025 89.54 10.46

13 1475 1164 1169 1479 1162 1474 8.6023 83.20 16.80

Figure 8: Measured vessel width showing by the white lines

in an image portion.

Canon D-60 digital fundus camera) with manually

measured width on different cross-sections from

Eye and Ear Hospital, Victoria, Australia. For each

cross-section, we received the graded width by

ﬁve different experts who are trained retinal vessel

graders of that institution. For manual grading a

computer program was used where the graders could

zoom in and out at will, moving around the image

and selecting various parts. We applied our technique

on these images to produce the edge image and vessel

centreline image. We considered these images and

randomly picked ninety-six cross-sections of vessels

varying width from one to twenty-seven pixels. We

measured the width for each cross-section by our

automatic width measurement technique (we call it

automatic width, A) and considered the ﬁve manually

measured width (we call it manual width) by experts.

We calculated the average of the manual width

(µ), the standard deviation on manual widths (σ

)

and considered the following formula to ﬁnd the error,

E =



(µ−σ

)−A

(µ−σ

)

(µ+σ

)−A

(µ+σ

)



1−

µ×A

−σ



(13)

In equation (13), we considered (µ ± σ

) to normal-

ize it. This formula is a good measure as the error

rate will be less if it is within the interval one stan-

dard deviation. With this formula, we calculated the

error and accuracy in all ninety-six cross-section and

achieve an average of 95.8% accuracy (maximum ac-

curacy is 99.58% and minimum accuracy is 83.20%)

in the detection of vessel width. We found the max-

imum error is 16.80% which is 2.04 pixel and the

minimum error is 0.698% which is 0.139 pixel. Ta-

ble 1 and 2 depict the manual and automatic width

measurement accuracy on different cross-sections in

an image. We compared our technique with (Lowell

et al., 2004) which achieved the maximum accuracy

of 99% (did not mention the average accuracy for all

cross-sections) with minimum pixel error of 0.34. Us-

ing the same formula, |(µ−A)/µ|), we achieved 100%

accuracy. Clearly, our technique is performing better.

7 CONCLUSIONS AND FUTURE

WORK

In this paper we proposed a new and efﬁcient tech-

nique for blood vessels width measurement. This ap-

proach is a robust estimator of vessel width in the

presence of low contrast and noise. The results ob-

tained are promising and the detected width can be

used to measure different parameters (nicking, nar-

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

184

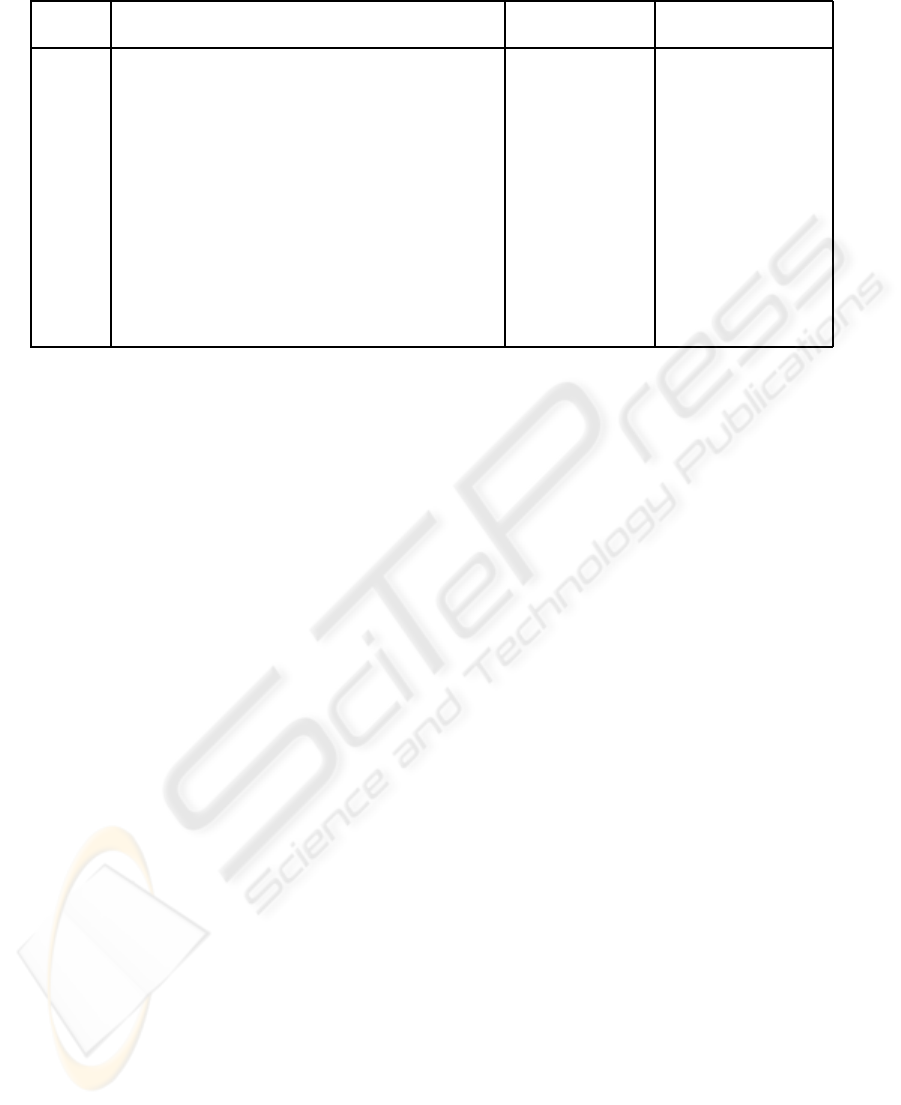
Table 2: Manually measured widths for an image cross-sections.

Cross- Manually measured width (in Micron) Mean width (µ) Standard Deviation

section One Two Three Four Five (in pixel) (σ

)

1 112.42 117.53 107.31 117.53 112.42 22.2 0.8366

2 107.31 112.42 107.31 117.53 107.31 21.6 0.8944

3 66.43 76.65 61.32 71.54 61.32 13.2 1.3088

4 61.32 71.54 61.32 71.54 56.21 12.6 1.3416

5 56.21 66.43 56.21 66.43 66.43 12.2 1.0954

6 107.31 107.31 102.2 102.2 97.09 20.2 0.8366

7 56.21 66.43 45.99 61.32 66.43 11.6 1.6733

8 86.87 107.31 102.2 107.31 97.09 19.6 1.6733

9 132.86 127.75 112.42 132.86 107.31 24 2.3452

10 45.99 51.1 35.77 56.21 35.77 8.8 1.7889

11 40.88 56.21 35.77 45.99 45.99 8.8 1.4832

12 35.77 51.1 45.99 56.21 40.88 9 1.5811

13 35.77 45.99 35.77 45.99 30.66 7.6 1.3416

rowing, branching coefﬁcients, etc.) for diagnosing

various diseases. Currently, we are working on the

blood vessels’ bifurcation and cross-over detection

where the measured width is contributing as an im-

portant information for perceptual grouping process.

ACKNOWLEDGEMENTS

We would like to thank David Grifﬁths (Research As-

sistant, The University of Melbourne and Eye and Ear

Hospital, Melbourne, Australia) for providing us with

the manually measured width images and data.

REFERENCES

Bezdek, J. (1981). Pattern recognition with fuzzy objective

function algorithms. Plenum Press, USA.

Bhuiyan, A., Nath, B., and Chua, J. (2007a). An adaptive

region growing segmentation for blood vessel detec-

tion from retinal images. Second International Con-

ference on Computer Vision Theory and Applications,

pages 404–409.

Bhuiyan, A., Nath, B., Chua, J., and Kotagiri, R. (2007b).

Blood vessel segmentation from color retinal images

using unsupervised classiﬁcation. In the proceedings

of the IEEE International Conference of Image Pro-

cessing.

Brinchman-hansan, O. and Heier, H. (1986). Theoritical re-

lations between light streak characterstics and optical

properties of retinal vessels. Acta Ophthalmologica,

179(33).

DRIVE-database (2004). http://www.isi.uu.nl/research/

databases/drive/, image sciences institute, university

medical center utrecht, the netherlands.

Gao, X., Bharath, A., Stanton, A., Hughes, A., Chapman,

N., and Thom, S. (2001). Measurement of vessel

diameters on retinal images for cardiovascular stud-

ies. Proceedings of Medical Image Understanding

and Analysis, pages 1–4.

Geusebroek, J., Boomgaard, R. V. D., Smeulders, A. W. M.,

and Geerts, H. (2001). Color invariance. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

23(2):1338–1350.

Gonzalez, R. C., Woods, R. E., and Eddins, S. L. (2004).

Digital image processing using matlab. Prentice Hall.

Hoover, A., Kouznetsova, V., and Goldbaum, M. (2000).

Locating blood vessels in retinal images by piece-wise

threshold probing of a matched ﬁlter response. IEEE

Transactions on Medical Imaging, 19(3):203–210.

Kruizinga, P. and Petkov, N. (1999). Nonlinear operator for

oriented texture. IEEE Transactions on Image Pro-

cessing, 8(10):1395–1407.

Lowell, J., Hunter, A., Steel, D., Basu, A., Ryder, R.,

and Kennedy, R. L. (2004). Measurement of reti-

nal vessel widths from fundus images based on 2-d

modeling. IEEE Transactions on Medical Imaging,

23(10):1196–1204.

Wu, D., Zhang, M., and Liu, J. (2006). On the adaptive de-

tetcion of blood vessels in retinal images. IEEE Trans-

actions on Biomedical Engineering, 53(2):341–343.

Wyszecki, G. W. and Stiles, S. W. (1982). Color science:

Concepts and methods, quantitative data and formu-

las. New York, Wiley.

Zhou, L., Rzeszotarsk, M. S., Singerman, L. J., and Chokr-

eff, J. M. (1994). The detection and quantiﬁcation of

retinopathy using digital angiograms. IEEE Transac-

tions on Medical Imaging, 13.

AN EFFICIENT METHOD FOR VESSEL WIDTH MEASUREMENT ON COLOR RETINAL IMAGES

185