MICROGLIA MODELLING AND ANALYSIS USING L-SYSTEMS

GRAMMAR

Herbert F. Jelinek and Audrey Karperien

School of Community Health, Charles Sturt University, Albury, Australia

Keywords: Microglia, L-systems grammar, modelling, pathology.

Abstract: Medical image analysis requires in the first instance information on the extent of normal variation in a

biological system in order to identify pathological changes. MicroMod is an L-systems based software

package available through the World Wide Web that allows modelling of complex branching structures

such as neurons and glia using deterministic or probabilistic algorithms. In addition, MicroMod includes

software for assessing complex structures using methods such as fractal and lacunarity analysis. We

demonstrated through fractal analysis of simulated microglia that MicroMod can be used for modelling and

measuring different stages of microglial activation. The fractal dimensions of microglia visualised using

histochemical techniques showed good agreement with our models made using MicroMod, and changes in

complexity and heterogeneity as seen during activation and response to pathology were well emulated by

modifying a few essential parameters (sub to parent branch length, sub to parent branch diameter, and sub

branch number). These results indicate that MicroMod provides a useful adjunct to neuroscience research

into understanding complex changes in structure associated with normal function and disease processes.

1 INTRODUCTION

The modelling programme described and discussed

here was inspired from research into the morphology

of a type of cell called microglia. These small cells

are a critical component of the brain’s immune

system, and have been called the brain’s “first line

of defence” for the critical roles they play in

mediating effects of injury and disease in the central

nervous system. (Kreutzberg 1995)

The feature of microglia particularly relevant to

this paper is their dynamic morphology. To explain,

microglia normally reside in the brain in a highly

branched resting morphology. In this form,

microglial cell bodies are small and elongated or

rounded, surrounded by multiple relatively thin

extensions known as microglial processes that

themselves branch to finer and finer levels of

ramification, extending around neurons and other

cells deep into the surrounding neural tissue, as

illustrated in Figure 1.

Resting microglia are thus perfectly postured to

continually sample their environment and respond to

the earliest signs of insult or injury in the

surrounding structures and milieu of the central

nervous system, but their role goes beyond that of

patrolling sentinel. If they detect problems,

microglia can change dramatically from their

Figure 1: Resting microglia are highly branched immune

system cells found in the brain.

289

F. Jelinek H. and Karperien A. (2008).

MICROGLIA MODELLING AND ANALYSIS USING L-SYSTEMS GRAMMAR.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 289-294

DOI: 10.5220/0001059802890294

 SciTePress

highly ramified, resting sensor morphology to an

unbranched, rounded to amoeboid form that is

increasingly motile and phagocytic (Soltys,

Orzylowska-Sliwinska et al. 2005). As illustrated in

Figure 2, this change occurs along a continuum of

subtle to obvious differences in morphology.

Figure 2: Typical microglial morphologies. Processes

retract and the soma becomes rounder and expands as

microglia become increasingly activated to respond to

pathological changes.

The morphology a microglial cell might be found

to adopt reflects variables such as the cell’s position,

surroundings, and motion, but also generally

corresponds to differences in functional capacity and

activity. Indeed, the relative amounts of microglial

cells adopting certain morphological configurations

vary in different diseases and in different stages of

the progression of individual disease states (e.g., the

overall profile of microglial morphology typical in

schizophrenia can be differentiated from that in

Alzheimer’s disease) (Jelinek, Karperien et al.

2004). It is therefore essential to obtain a good

understanding of even subtle changes in microglial

form along the continuum of morphological variety,

and to be able to relate these changes to cell

characteristics (Cornforth, Jelinek et al. 2002).

1.1 The MicroMod Modelling Software

MicroModV6.0 is biological cell and fractal structure

modelling software written in Java by one of the

authors (AK), using the NetBeans IDE 3.5 on the

Java 2 Platform v1.4.2 (Jelinek, Karperien et al.

2002). The programme has been tested on

WindowsXP Pro, Windows2000, Windows98, and

SUSE Linux. It is available as a stand-alone Java

application from Charles Sturt University as

MModLE.jar (source code is available on request).

MicroMod contains 28,456 lines of code, 19,313

non-comment lines, and 7,818 comment lines of

code. Features available in MicroMod are shown in

Table 1.

In addition to the models described in the rest of

this paper, MicroMod software renders for

benchmarking and analysis statistical or

deterministic, skinny or fat fractals, including

quadric, Koch, Menger, and Sierpinski fractals;

multifractals such as various Henon Maps; other

iterated fractal structures (e.g., ferns); and diffusion

limited aggregates.

Table 1: MicroMod Features.

MicroModsrc Main package

MicroModsrc.GUI Graphic user interface

MicroModsrc.Help

User's guide in html for swing

browser

MicroModsrc.MakeSt

ructure

Methods for generating random

and deterministic fractals as well

as branching structures for cell

modelling

MicroModsrc.Utils Utilities

Structures can be viewed on a display screen or

saved to a hard drive as either images (.jpg or .png

format) or MicroMod model files (.mod format). All

models can be rendered and saved in coloured,

shaded, gray-scale, and binary formats. Structures

are generated from built-in configurations or

loadable .mod files (some provided with

MicroMod), or from parameters set by the user.

Configurable options include structural parameters

and various rendering options such as background

colour or whether to view a structure grow or not.

All models can be modified, saved, and reloaded,

and can be used to generate single images or sets of

multiple images.

MicroMod also includes a fractal analysis

function. Structures can be assessed on the screen as

they are generated or in batches of images from the

user's hard drive. The analysis is delivered on screen

and in detail in a text file that can be loaded in a

spread sheet. The fractal analysis algorithms of

MicroMod are also available in the FracLac

software, a plug-in for ImageJ freely available from

the US National Institutes of Health (Karperien

2007).

2 MODELLING WITH

MICROMOD

To simulate biological structures such as microglia,

MicroMod employs L-systems principles. As

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

290

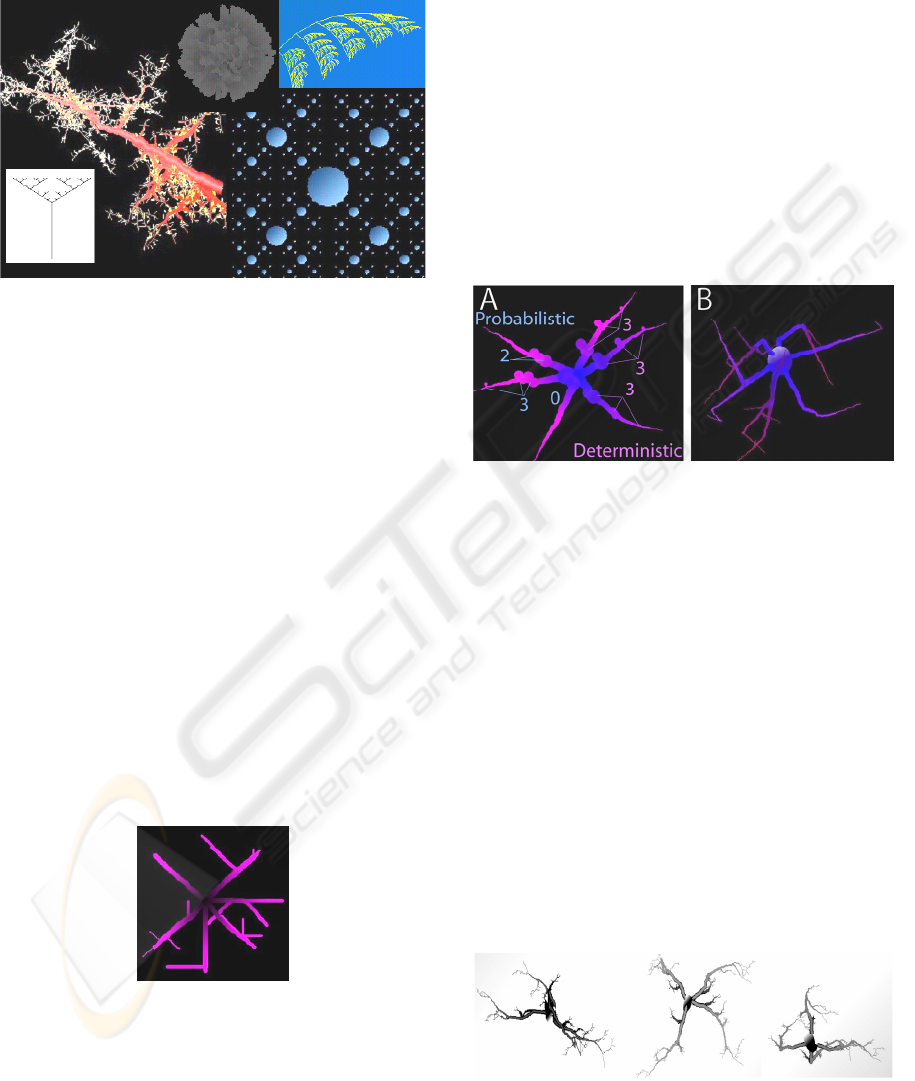
illustrated in Figure 3, a variety of structures at

different levels of complexity can be generated using

L-systems.

Figure 3: Examples of structures modelled in MicroMod

using L-systems principles.

The fundamental algorithm used for modelling

microglia is based on MicroMod’s built-in

branching model. The algorithm generates sets of

symbols to be rendered on the computer screen. For

modelling microglia, one set specifies features for

one microglial process, where each point within

each set specifies the size, shape, colour, and

location of a structural element of the process, and

rules set by the user are applied recursively to evolve

each original set into a more complex structure.

To elaborate, the simplest branching model is a

set of points representing straight lines, and the next

level of complexity is a set with one level of sub-

branches (Figure 4). Such a model can be altered by

changing various parameters including the rate of

acquiring branching points and the number of

branches that sprout at each branching point; the

ratio of the length and diameter of daughter branches

to the length of the parent; and the taper for each

branch.

Figure 4: Radial model generated by specifying a

minimum number of parameters.

Gross structural features such as the area and general

shape of the central soma and the number, length,

and diameter of primary branches can also be

changed. In addition, directional features such as the

probability of a branch continuing in a direction

(related to the tortuousness of a process) and the

angle of branching can be set. Moreover, to further

explore variation within a cell or compare cells, the

user can modify individual processes of a cell

separately.

Furthermore, several of the parameters

describing a process, such as branching rate and

tortuousity, can be applied as probabilities rather

than fixed values (Figure 5). Figure 5A, for instance,

illustrates a simple radial model generated using a

probability (rather than a deterministic value) for the

number of branches along each primary branch,

whereas Figure 5B shows a simple radial model

rendered with a deterministic branching rate but

probabilistic tortuousity features.

Figure 5: Simple branching models. Within each model,

all branches are statistically identical. 5A. Random

Variation in Branching Frequency. Nodes show locations

for daughter branches on primary branches. All nodes

were sprouted at one statistically identical rate; however,

nodes on branches extending right were generated

deterministically and on branches extending left were

generated probabilistically. 5B. Random Variation in

Branching Angle and Tortuousity. Daughter branches

were sprouted at one deterministic rate on all primary

branches, but their rate and angle of change in direction

were determined probabilistically.

The significance of having probabilistic

parameters available for modelling microglia is that

the opportunity exists to generate each cell process

as a statistically identical but unique structure. The

user can, accordingly, explore overall features of a

class of structures by generating groups of

statistically identical but unique images from a

single set of parameters (Figure 6).

Figure 6: Statistically identical but unique models of

resting microglia generated using one set of parameters.

MICROGLIA MODELLING AND ANALYSIS USING L-SYSTEMS GRAMMAR

291

As was noted in the introduction, microglia adopt a

wide variety of conformations when they respond to

events in nervous tissue. For modelling microglia

and other biological cells, MicroMod has several

models in addition to the radial model just discussed.

Examples of the MicroMod outputs of the Y-model,

the bushy and narrow models, and the B-model are

shown in Figure 7. The Y-model (top of Figure 7)

provides large spherical to amorphous structures

with short tapered and unbranched projections. The

bushy model and the narrow model are similar, but

allow branch diameters and the degree of sprouting

to be set. These models specify how tortuous images

are using the single angle functions in MicroMod.

The B-Model includes options for multiple,

bifurcating branches as well as for setting branch

angle, length, tortuosity and twist. The number of

branches and number of sprouts can be modified

using the menus.

Figure 7: Modelling options for branched cell structures

available in MicroMod.

3 ANALYSING MICROGLIAL

ACTIVATION USING

SIMULATED MICROGLIA

Populations of cells were modelled from real

microglia, based on measurements such as the length

and number of branches and the ratios of daughter to

parent branch length and diameter. To most closely

emulate real, dynamic microglia in their natural

environment, cells were generated using

probabilistic values. Using box-counting fractal

analysis we compared the simulated cells to the real

after converting digital images to binary in order to

assess the complexity of the cell contour. As

indicated in previous research, there was close

agreement between simulated and real cells (Figure

8) on the box counting dimension (D

). (Smith,

Marks et al. 1989; Jelinek, Karperien et al. 2002)

Figure 8: Real compared to simulated microglia. The real

cell had a fractal dimension of 1.423 compared to the

simulated of 1.425.

3.1 Scaling Features

To assess the sensitivity of MicroMod for modelling

subtle morphological changes associated with

different levels of microglial activation, we

manipulated several features of the models and

assessed both complexity as measured by the D

and

heterogeneity (lacunarity or Λ). Manipulating the

size and shape of the modelled soma had essentially

no effect on the D

, but a slight effect on Λ, where

in general models with larger and more elongated

somata had lower values for Λ. Both the D

and Λ

were affected by changing the number of primary

branches, but the effects were not consistent.

Changing scaling features, in contrast, had several

noteworthy effects. Changes were made in a manner

consistent with fractal changes, as the results are

predictable and therefore useful in judging the utility

of the software.

Figure 9 shows that the D

and Λ changed when

the length of sub-branches relative to the parent

branch was changed but the number of sprouts

remained the same. Similarly manipulating the scale

of sub to parent branch diameter and the number of

new branches per branch affected the D

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

292

Figure 9: Effect of varying cell features on fractal

dimension and lacunarity.

Changing the scaling of sub-branch diameter had

no effect on either the D

or Λ for models with

narrow branches, owing to the finite limit on the

smallest possible diameter of a branch. For models

with larger starting diameters, however, the ratio of

sub-branch to parent diameter affected the D

. The

and Λ were strongly positively correlated for

models with wider branches, but not as strongly for

models having narrower branches. The D

mainly

decreased as the length of primary processes

decreased, as when microglia withdraw their

processes in response to noxious stimuli in their

environment, for example. Although Λ decreased

overall with decreasing primary process length, it

initially increased for smaller branch diameters (i.e.,

models resembling resting more than activated

cells).

Cells differing only in branch diameter were

modelled to emulate process swelling in isolation

from other changes—i.e., only the diameter of

primary branches (measured where they leave the

soma then allowed to taper according to a fixed rate)

was manipulated. Both the D

and Λ were affected

by changing this feature, but there were some

differences in the effects. As long as branch

diameter remained relatively narrow compared to

soma span, the D

rose slightly as branch diameter

increased. As branch diameter continued to increase,

however, owing to crowding of "swollen" processes,

some detail disappeared from the final binary

patterns extracted from the images. In contrast, Λ

decreased without increasing as branch diameter

increased, and the effect was more noticeable at

smaller diameters than it was for the D

. In addition,

models with greater tortuousity had higher D

and

lower Λ values.

4 CONCLUSIONS

Previous research has shown that microglial

morphology can be modelled with high fidelity

using MicroMod. In addition, recent investigations

have revealed that the D

and Λ can be used to

measure the types of graded changes in microglial

morphology typically associated with microglial

activation. (Jelinek, Karperien et al. 2002) The work

presented here goes a step further in describing how

the progression from ramified to activated (i.e.,

nonpathological to pathological) in microglia can be

accurately modelled and cellular complexity

assessed by progressively changing a few essential

parameters.

It is important to note that the modelling of

microglial activation described here is deliberately

subject to random variation. For perfect patterns

extracted from perfect theoretical models, the D

measures fundamental complexity and Λ measures

heterogeneity. From a practical perspective applied

to real cells, though, they will measure at once a

composite of several features. Because of the

considerable morphological variation attributable to

not only activation but also the space microglia

occupy and the orientation they assume at any point

in time, variation is predictable when finding D

even for cells in equivalent activation states having

essentially the same branching ratios. As was shown

here, despite that a microglial model's inherent

complexity is specified by known recursively

applied rules, an extracted pattern may not

necessarily convey this fundamental pattern's

original information fully and without distortion. In

real cells, the underlying mechanisms of

morphological transformation are also not

necessarily conveyed in values extracted from real

contexts. But microglia are biological structures we

hope to understand and assess ultimately in their

natural environs. Analyses that can be used in this

way have practical advantages over assessments

based on uncomplicated theoretical models, and

modelling, as was shown here, helps bridge our

knowledge of practical influences.

In conclusion, the work we report here may have

important implications for understanding the events

of microglial activation associated with different

states of health and disease. Simulated cells, readily

available in large numbers and extremely

manipulable, increase the opportunities to

objectively study morphological changes and

random variation in microglia. MicroMod, thus,

presents a useful adjunct to neuroscience research

into understanding complex changes in structure

associated with normal function and disease

processes.

MICROGLIA MODELLING AND ANALYSIS USING L-SYSTEMS GRAMMAR

293

REFERENCES

Cornforth, D., H. F. Jelinek, et al. (2002). Fractop: a tool

for automated biological image classification. 6th AI

Australasia-Japan Joint Workshop, Australian

National University, Canberra.

Jelinek, H. F., A. Karperien, et al. (2004). Differentiating

grades of microglia activation with fractal analysis.

Proceedings of the Complex Systems Conference,

Cairns, Australia, IOS Press.

Jelinek, H. F., A. Karperien, et al. (2002). MicroMod - an

L-systems approach to neuron modelling. 6th AI

Australasia-Japan Joint Workshop, Australian

National University, Canberra.

Karperien, A. (2007). FracLac for ImageJ. FracLac for

ImageJ 2000-2007. Bethesda, Maryland, Research

Services Branch, National Institutes of Health:

Morphological digital image analysis software for

fractal, multifractal, lacunarity, and other

morphometrics.

Kreutzberg, G. W. (1995). "Microglia, the first line of

defence in brain pathologies." Arzneimittelforschung

45(3A): 357-60.

Smith, T. G., W. B. Marks, et al. (1989). "A fractal

analysis of cell images." Journal of Neuroscience

Methods 27: 173-180.

Soltys, Z., O. Orzylowska-Sliwinska, et al. (2005).

"Quantitative morphological study of microglia cells

in the ischaemic rat brain using principle component

analysis." Journal of Neuroscience Methods.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

294