
A HYBRID METHOD BASED ON FUZZY INFERENCE AND
NON-LINEAR OSCILLATORS FOR REAL-TIME
CONTROL OF GAIT
J. C. Moreno
1,2
, J. L. Pons, E. Rocon
1
Bioengineering Group, Industrial Automation Institute, the Spanish National Research Council (CSIC), 28500 Madrid, Spain
2
Technaid S.L., 28500 Madrid, Spain
Y. Demiris
Intelligent Systems and Networks Group, Imperial College London, SW7 2BT London, UK
Keywords:
Fuzzy inference systems, non-linear oscillators, inertial sensing, gait compensation.
Abstract:
Robust generation of motor commands for real-time control of locomotion with artificial means is crucial for
human safety. This paper addresses the combination of fuzzy inference for determination of rules with a non
linear oscillator system, as generators of motor commands for the control of human leg joints during walking,
by means of external gait compensators, e.g. exoskeletons, functional electrical stimulation or hybrid systems.
The response of the proposed method is evaluated for variations in stride frequency and step length. The
testing during gait conditions is performed considering inertial sensing as feedback in a simulation study. The
reference data considered is obtained in multiple experiments with healthy subjects walking with a control-
lable exoskeleton designed to compensate quadriceps weakness. A model of the operation of the knee joint
compensation provided by the exoskeleton is obtained as reference to evaluate the method based on real data.
The results demonstrate the benefits of both incorporating a) the fuzzy inference system in cyclical decision
making for generation of motor commands and b) the dynamic adaptation of the timing parameters of the
external compensator provided by the van der Pol oscillator.
1 INTRODUCTION
Robust generation of motor commands for real-time
control of locomotion with artificial means is cru-
cial for human safety. Broadly, current active ex-
ternal compensators of pathological gait under re-
search can be configured as functional electrical stim-
ulators (FES), (Popovic et al., 1999), (Skelly and
Chizeck, 2001) controllable leg exoskeletons or or-
thoses, (Blaya and Herr, 2004), (Irby et al., 1999),
(Moreno et al., 2005) or as a combination of both,
known as hybrid systems, (Gharooni et al., 2000),
(Goldfarb and Durfee, 1996). From the control point
of view, the design of robust controller of locomo-
tion with such devices, towards real life application,
must be easy to customise, adapt dynamically to typ-
ical variations in gait pase and preferably should in-
corporate a coordinated development with the user.
1.1 Gait Compensation
A wide range of external gait compensators, e.g. ex-
oskeletons, functional electrical stimulation or hybrid
systems, have been considered to restore human gait.
In particular leg exoskeletons or orthoses, can be pre-
scribed for cerebrovascular accident, polyo myelitis
or cerebral palsy patients with leg muscle weakness,
in order to provide knee stability, reducing falling risk
and enabling a certain degree of mobility.
In order to control an exoskeleton, it is not clear
the hypothesis that instantaneous control of trajec-
tory of the joint angle is essential for the lower limb
system, since the reduced mechanical output —joint
torque— limits its transitory response, in relation with
the inertial properties of the musculoskeletal system
(Franken, 1995). Velocity or position control loops
are more appropriate and safe in training and reha-
bilitation applications where controlled generation of
joint trajectories is required, with application of oscil-
latory signals and modulation techniques during gait
44
C. Moreno J., L. Pons J., Rocon E. and Demiris Y. (2008).
A HYBRID METHOD BASED ON FUZZY INFERENCE AND NON-LINEAR OSCILLATORS FOR REAL-TIME CONTROL OF GAIT.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 44-51
DOI: 10.5220/0001060800440051
Copyright
c
SciTePress

E
Swing
Stance
Figure 1: Mechanical adaptation for gait compensation dur-
ing one gait cycle at the knee joint.
cycles for training subjects following neural/motor in-
juries.
Our previous work has consisted in the implemen-
tation of intermittent control of resistance of the knee
joint with an unilateral exoskeleton applying selec-
tively different constant stiffnesses depending on gait
phase, to approach more natural profiles and avoid
collapsing of the knee and risk of falling, see fig. 2.
Linearsolenoid
Sensorset
Anklepassive
actuatorand
carbonfiberinsole
Controller
Kneeactuator
Figure 2: Controllable ambulatory exoskeleton.
Under this approach, a knee actuator is controlled
to apply a given impedance K
1
in the stance phase,
during a period of time ensuring the joint stability
and shift during swing phase releasing the joint for a
free swing while applying K
2
(K
1
>> K
2
), for smooth
transition and storage/recover of energy to assist the
leg extension, see figure 1.
1.2 Rule based Control
Reliability of control in such a wearable solution for
pathological cases is a critical issue that has an impact
in human safety.
Figure 3: Typical normal gait pattern of foot and shank seg-
ments rotations and rotational velocities (sagittal plane) dur-
ing a walking task at 34 m/min speed, with the cable-driven
exoskeleton, after training of the subject. A system with a
cable triggers the knee mechanism (onset) depending on a
fixed degree of dorsiflexion.
The output of the controller is the motor com-
mand for the actuator, characterized by two param-
eters: activation onset and period. The activation on-
sets during each stride are calculated by rule-based
conditions, evaluated according to segments orienta-
tion or rate velocity (See pattern during stance phase,
figure 3). The system is a reactive controller perform-
ing according to the motion of the leg. The criteria to
cyclically adapt the activation period (pulse width) of
the actuator is defined considering temporal parame-
ters relative to stance phase of current S(k) and past
S(k-1) strides, and initial conditions S(0), given by
average expected values.
Rule-based
condition
y
Intermittent
mechanism
Leg
dynamics
Linearsolenoid
excitation
b(k)
w
f s
w
Figure 4: Control scheme for walking.
Experimental trials have demonstrated short-term
adaptation of human motor system when apply-
ing functional compensations with customized tun-
ning of the discrete rule-based controllers ,(Moreno,
A HYBRID METHOD BASED ON FUZZY INFERENCE AND NON-LINEAR OSCILLATORS FOR REAL-TIME
CONTROL OF GAIT
45

2006). The adaptation of cyclical activation, has
demonstrated proper results at self-preferred constant
speeds. The next proposed method is an improvement
intended to provide the required dynamicaladaptation
to changes of step frequency/length by the user.
1.3 Bipedal walking with Central
Pattern Generators (CPGs):
Simulation
It has been demonstrated previously how the use of
the dynamical systems paradigm can realize a walk-
ing behavior in robotic walking platforms (Veskos
and Demiris, 2006). The neural architecture has
demonstrated successful operation in swinging and
planar walking in a bipedal platform, incorporating
van der Pol oscilators as generators of motor com-
mands.
Medium and short term application of a walking
real-time controller for the mentioned application sce-
narios, ought include mechanisms that provide adapt-
ability and stable response to variations of frequency
in the feedback signals, can led to an approach of co-
operative development with the user/environment. In
the following, the analysis of the response of the pro-
posed hybrid controller to variations in gait frequency
is evaluated with real data measured with the orthotic
walking platform.
2 METHODS
2.1 Gait Patterns with Knee Joint
Compensator
Subjects wearing an exoskeleton, need to adapt their
walking strategy to drive the system to successfully
switch between two knee spring damper configura-
tions. During the entrainment of the subject with the
controllable exoskeleton it is necessary to reach a cer-
tain ankle dorsiflexion angle which is variable during
normal gait. Although this angle is adjustable, sub-
jects change their gait pattern until they learn to use
the exoskeleton. The learning process (which can be
seen as an adaptation) in the use of the controllable
exoskeleton has been previously studied in (Forner-
Cordero et al., 2006). In order to obtain sampled
data of different gait speeds, experimental trials with
a healthy subject have been conducted after the adap-
tation process, consisting in walking back and forth
along a 10 meter path, with definition of the step
length with marks on the floor and the gait speed by
means of a metronome, and systematic adjustments
of the cable mechanism to provide a comfortable gait
pattern (see table 1). The gait velocity and step length
variations were defined according to average values
taken from Perry, (Perry, 1999), consisting in feasi-
ble combinations of 100%, 70%, 60% and 50%. Rate
gyroscopes fixed at the shank and leg segments of the
external device were used to measure rotational veloc-
ities along the sagittal plane. Motions of interest oc-
cur at normal (2.6 km/h) and low (2 km/h) gait speeds,
and therefore, signals outside the band frequency re-
lated to gait kinematics (0.3–20 Hz), are rejected from
the sensor outputs with -3 dB low pass filters, refer
(Moreno et al., 2006) to for details. A precision angu-
lar position sensor was fixed at the knee joint to track
the knee joint angle in the sagittal plane. A resistive
pressure sensor (5 mm in diameter active area, 0.30
mm thickness) is used to monitor the activation status
of the knee actuator.
Collection of input/ouput data is utilized to gener-
ate training and checking data sets, of both multiple
speed trials, and constant speed separated trials.
2.2 Validation Model
A robust Model describing the dynamics of the knee-
orthotic hinge system during cyclic walking condi-
tions can be used as a reference to analyze the per-
formance of the advanced control system. We pro-
pose the identification of the model the activation pat-
terns provided by the cable driven exoskeleton, with
time-series of kinematic data. A broadly used signal
processing paradigm is the state-space model. De-
fined by two equations, the state-space model has
been broadly applied in signal processing (Smith and
Brown, 2003). A first equation describes how the hid-
den state or latent process is observed and a second
(state) equation that defines the evolution of the pro-
cess through time. Based on the formulation given by
(Haverkampet al., 1996), we proposeidentification of
a multiple-input single-output continuous-time model
from the experimentally collected input and output
data.
Considering the state-space model in the innova-
tions form
dx(t)
dt
= Ax(t) + Bu(t) (1)
y(t) = Cx(t) + Du(t) (2)
where u(t) denotes the sampled inputs, being the
foot and shank rotations in the sagittal plane dur-
ing walking, for continuous measurements at 100 Hz
sampling frequency, with transitions from low to high
speed, and progressive variations in step length and
given the measured output reference; y(t), as the en-
trained knee joint status (actuator activation period)
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
46

Table 1: Systematic variations of healthy subject walking with the cable driven prototype (* Not feasible combinations).
Percentage Step length[m] Stride length[m] Speed[m/s]
100 0.73 1.46 1.35 0.94 0.81 0.67*
70 0.51 1.02 0.94* 0.66 0.56 0.47
60 0.44 0.88 0.81* 0.56 0.48 0.40
50 0.37 0.73 0.67* 0.47 0.40 0.33
Cadence (step/min) 111 78 67 56
Metronome (bpm) 1.85 1.30 1.11 0.93
for normal walking, x(t) is the internal state of the
system and [A, B,C, D] are the deterministic system
matrices.
The reference sampled input and output data u(t)
and y(t) is obtained from experiments with healthy
subjects wearing a orthotic walking platform, manu-
ally adjusted at each velocity to trigger the knee actu-
ator based on the ankle dorsiflexion.
The goal of the state-space model identification
process implemented in MATLAB is to find the sys-
tem matrices [A, B,C, D] according to the model struc-
ture. This resulted in a second order model as the best
to the input-output behavior of the system, selected
upon the analysis of the singular values (1st order,
53.23; 2nd order, 3.77; 3rd order, 0.34; 4th, 0.30).
The continuous-time model describes the relation
between the foot and shank segments angular veloci-
ties and the output activation at the knee joint actuator
for the range of tested speeds, by the state differential
equation 1 and the output equation 2, where
A =
0.994 −0.063
−0.003 0.933
; (3)
B =
−3.05e
−6
−8.28e
−6
−2e
−5
−3.39e
−5
; (4)
C =
14.55 −0.009
; (5)
Assuming the initial state as zero, from the evalu-
ation of the transient (impulse) response of the second
order system, it can be concluded a stable system with
t
p
= 0.5 s, as the time to reach the peak value, and a
settling time t
d
of approximately 10 s, after persistent
excitation.
Evaluation of the response of the model compared
against the external compensator operation is then
performed, with the checking data set corresponding
to multiple speeds. The crossing zeros (time inter-
polation) of the oscillatory output signal during the
steady state are detected as equivalent onset and offset
timings of the measured events. The correlation coef-
ficient r
2
, calculated for the modeled and measured
outputs is 0.999.
2.3 Architecture
The control scheme consists of different modules (see
figure 6). A fuzzy inference system with two inputs
and a single output node is identified and trained to
map the inputs and trigger the actuator. The crisp out-
put of the fuzzy inference system during each cycle
is critical in providing transition between restrained
knee flexion in stance to a free swinging leg. The
activation period of the knee actuator (pulse width)
during the swing phase is cyclically adapted by a
second module composed by an nonlinear oscilla-
tor. This nonlinear system incorporates real-time es-
timated gait temporal parameters as feedback in the
generation of an oscillatory signal which adapts the
duty cycle of an external compensator.
2.3.1 Fuzzy Inference System
Conventional PID controllers have been applied in the
control of cyclical movements in legs of paraplegic
subjects (Franken, 1995). Introduction of dynamical
adaptation of the rules commanding FES systems has
been investigated, in order to cover a wider range of
unsafe and uncertain situations in application of stim-
ulation . A Sugeno system is suited for modeling non-
linear systems. A training scheme with a fuzzy mod-
eling network structure has been combined to develop
a gait synthesis learning scheme, (Horikawa et al.,
1990).
Obtaining a fuzzy system corresponds with ap-
proximated reasoning, which refers to methodologies
to describe physical systems which include complex-
ity due to nonlinearities and uncertainties. Let us sup-
pose that our unknown system is a black box only ca-
pable of measuring a set of inputs x
1
,...,x
n
and outputs
y
1
,... ,y
m
. A fuzzy system with a crisp output and the
following type of rules is to be obtained
R
i
: IF x
1
es S
i1
and...and x
m
es S
im
, THEN and es c
i
(6)
The fuzzy inference system is generated by means
of the grid partition method. For the identification a
A HYBRID METHOD BASED ON FUZZY INFERENCE AND NON-LINEAR OSCILLATORS FOR REAL-TIME
CONTROL OF GAIT
47

0
20
40
60
Angle [°]
−400
−200
0
200
400
Ang. Velocity [°/s]
−200
0
200
Ang. Velocity [°/s]
10 15 20 25 30 35 40 45 50
off
on
Time [s]
Error
Time[s]
0
0.16(+)
0.73(−)
Knee status
1.35
0.94 0.81 0.66
0.56 0.47 0.56 0.48 0.4 0.47 0.4 0.33 Gait Speed
Knee
Foot
Shank
1.85
1.30
1.30
1.30 1.30
1.11
1.11 1.11 1.11 0.93
0.93 0.93 Stride length
Figure 5: Data of measured input/ouputs of healthy subject with the compensator, after adaptation, at multiple gait speeds
and space-state model performance. (a) Knee joint measured angle with external compensation, checking data set of (b) Foot
angular velocity and (c) Shank angular velocity; (d) the measured activation status of the actuator (dotted line), model ouput
(dashed line) onset and offset timings given by the model (circles), and time difference per cycle.
FuzzyInference
System
x: w w
f s
,
Knee
Actuator
Lowerlimb
dynamics
MotorCommand
Generator
NonlinearPattern
Generator
w w
f s
,
du/dt
onset
y (k+ )
m
D
f:
b
Pulsemod.
width
Figure 6: Hybrid architecture for control of gait external compensation at knee level, based on inertial sensing data. First
module contains the fuzzy inference system with a crisp output The second module contains a nonlinear system predicting
the activation period of the knee actuator as function of gait frequency (forced oscillator), with proprioceptive feedback.
training data set is generated from the experimenta-
tion. The identification method consists in the appli-
cation of the adaptive network fuzzy inference system
(ANFIS) proposed by Jang, (Jang, 1993), in order to
build the fuzzy rules with membership functions to
generate input/output data pairs. Iteratively, input pa-
rameters of the membership functions are learnt by
means of back-propagation in an adaptive network
and while the parameters of output functions are opti-
mized by the least squares fitting method. The adap-
tive network is a feedforward multilayered network,
with a supervised learning scheme. The functions of
given nodes in a layer are similar. For means of sim-
plicity, we consider a first order Sugeno type model,
as the inference system. Having the kinematic inputs,
the output E(t) and n fuzzy rules:
R
n
: IF
˙
θ
s
is A
n
, AND
˙
θ
f
is B
n
THEN E = p
1
˙
θ
s
+
˙
θ
f
+ t
(7)
Gaussian membership functions have been se-
lected for smooth transition. A total of 4 Sugeno
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
48

type fuzzy rules were defined, with a network with
21 nodes. These rules were of AND (minimum) type
antecedent. The defuzzification method, calculating
the output, is performed by the centroid method. The
clustering radius r = 0.2 was adjusted for tunning.
The optimization process spanned 13 epochs, with the
training data set. The figure depicts the output surface
of the final identified system given the two inputs.
−200
−100
0
100
200
−200
−150
−100
−50
0
50
100
−10
−8
−6
−4
−2
0
2
4
Foot angular velocity [°/s]
Shank angular velocity [°/s]
Output
Figure 7: Inputs (foot and shank angular velocities) output
(knee actuator activation) surface of the fuzzy system.
2.3.2 Forced Nonlinear Oscillator
The dynamic robustness of a pattern generator to
noise and other external disturbances can be improved
by incorporating nonlinearities to the system. A van
der Pol oscillator, requires a reduced number of pa-
rameters, and has the advantages of robustness and
ease of computational implementation. Such nonlin-
ear system can be applied as an adaptive oscillator
during the swing phase to determine the time of acti-
vation of the external compensator. To unlock the fre-
quency of the oscillator and provide it with adaptabil-
ity to the leg motion, the nonlinear system is forced to
oscillate at a frequency, which depends on the spatio-
temporal behavior of gait. Let us consider the forced
nonlinear oscillator
[!top] ˙x = y (8)
˙y = − µ(x
2
− 1)y− ωx+ Acosθt (9)
with ω as the natural frequency µ as the damping
parameter, θ as the forcing frequency and A as the
amplitude of the forcing function. An approximate
solution of the non-linear system, satisfying the initial
conditions x = 0, y = 0 is calculated during each cycle
i with
θ
i
=
T
ST
R
(10)
where T
ST
is the stance phase period in cycle i,
and R, a frequency scaling factor. T
ST
is estimated
from consecutivelocal minima (peak) values from the
foot rotational velocity, as described in (Moreno et al.,
2006).
2.4 Hybrid Controller
Local minima values are detected from the output of
the fuzzy system, upon numerically integration. The
sensitivity of the local minima detector is given by
δ, which corresponds to the minimum difference in
amplitude with the neighbor samples. With the cali-
brated gyroscopes raw data, a δ = 40 was satisfactory
for all conditions. Thus, cyclically the fuzzy system
provides the activation onset, the controller incorpo-
rates the output of the nonlinear oscillator to predict
the width τ or duration period for the knee external
compensator, with
τ =
D
2ω
(11)
where D determines the duty cycle percentage. In-
corporating the prediction given by the forced oscilla-
tor, D = 0.8 was defined and remained constant in all
further experiments.
An example of the hybrid controller for cyclic gait
at 0.94 m/s (stride length, 1.46 m) is depicted in fig. 8
3 RESULTS
The performance of the hybrid controller is compared
with the validation model and the testing data set. The
mean errors and standard deviations are calculated,
considering 4 continuous gait cycles per each con-
dition, for the output of the fuzzy inference system
module and the nonlinear oscillator module (see Table
2). A negative error (in seconds) means anticipation
with respect to the reference. For the tested condi-
tions, the maximum average error for the fuzzy rule-
based detection was 0.19 s demonstrating the robust-
ness of a single fuzzy model to drastic variations in
stride frequency. The discrete rule-basedmethod, pre-
vious tests showed significantly better performance
for the application of thresholds, during slow gait ve-
locities in comparison with the results with higher
velocities. The response with the fuzzy rule-based
method can be regarded as uniform for the tested con-
ditions. The maximum average error for the oscillator
was 0.32 s and therefore, the robustness to the varia-
tions in the timing of the generated motor commands
was observed. The evaluation with the continuous
data set provide a good indication of the accuracy and
robustness of the hybrid method.
A HYBRID METHOD BASED ON FUZZY INFERENCE AND NON-LINEAR OSCILLATORS FOR REAL-TIME
CONTROL OF GAIT
49
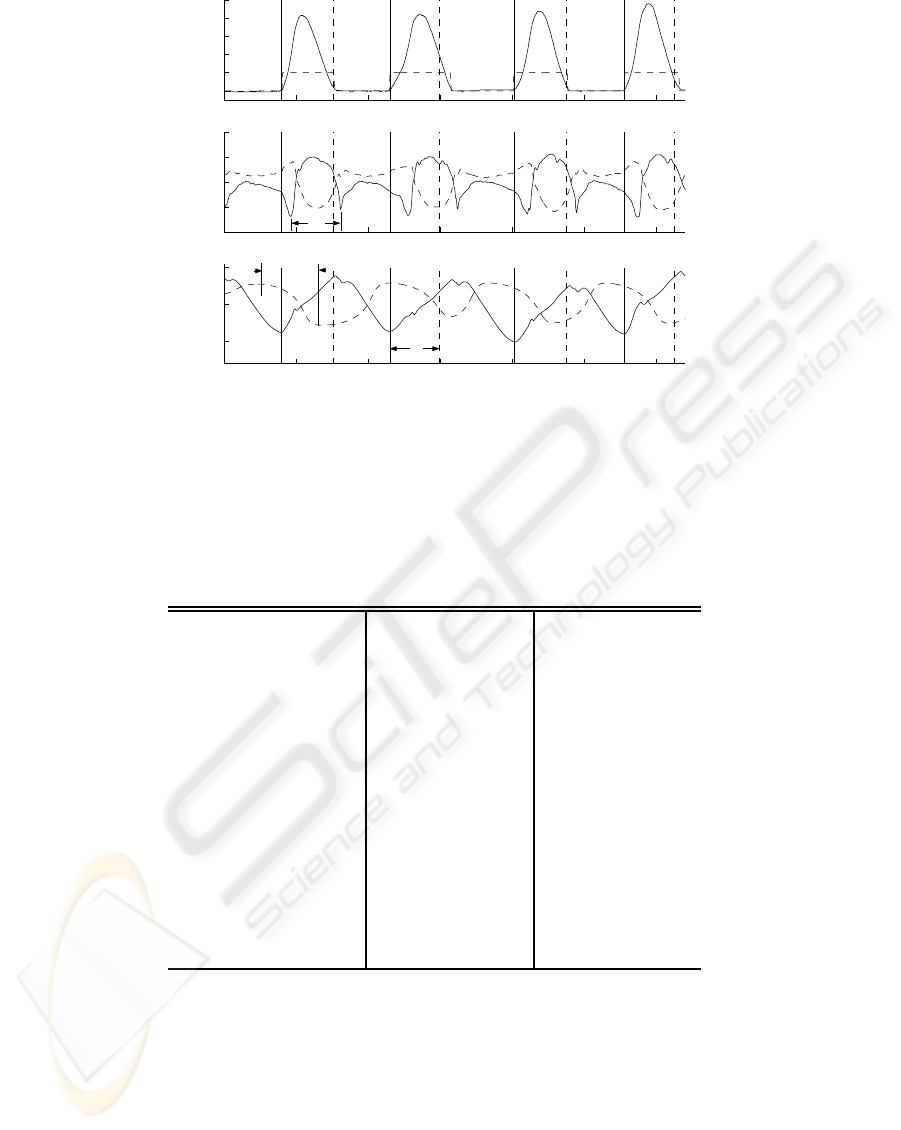
0
10
20
30
40
50
Knee sagital (continuous) − Validation model output (dashed)
Knee angle [°]
−400
−200
0
200
400
Shank segment (continuous) − Foot (dashed)
Angular velocity [°/s]
0 100 200 300 400 500 600
−200
0
200
Fuzzy Inference System Output (continuous) − Forced oscillator y ouput (dashed)
Sample
Amplitude
τ
1/2ω
T
ST
Figure 8: Example of the simulation results of the hybrid system at a relative fast speed. Measured knee angle and reference
output given by validation model (top); Inputs (middle); Fuzzy inference system and forced linear oscillator outputs. The
hybrid system generates the triggers (continuous vertical lines) and activation periods (dashed vertical lines).
Table 2: Results of the hybrid controller for the 12 testing conditions. Mean errors and standard deviations with respect to the
evaluation model output are calculated taking 4 continuous gait cycles per each condition.
Fuzzy System Forced oscillator
Step length[m] Speed [m/s] Mean error [s] SD Mean error [s] SD
1.46 1.3505 0.0995 0.0123 0.005 0.0451
1.46 0.94535 0.041 0.0744 -0.025 0.0719
1.46 0.8103 0.154 0.1847 -0.245 0.0806
1.022 0.6617 0.0685 0.0296 -0.06 0.051
1.022 0.5672 -0.042 0.0238 -0.17 0.0497
1.022 0.4726 -0.13 0.1238 -0.1775 0.1072
0.876 0.56721 0.0335 0.023 -0.1275 0.0629
0.876 0.48618 -0.0125 0.0728 -0.1725 0.083
0.876 0.4051 -0.1075 0.12 -0.32 0.0668
0.73 0.47267 0.0025 0.031 -0.16 0.0462
0.73 0.4051 -0.1205 0.0689 -0.0625 0.0998
0.73 0.3376 -0.1915 0.1003 0.15 0.2149
4 CONCLUSIONS
The evaluation with the continuous data set provide a
good indication of the accuracy and robustness of the
hybrid method. For the tested conditions, the results
demonstrate a proper means to combine a learning
method which incorporates fuzziness with the adap-
tive nature of a non lineal oscillator, to generate mo-
tor commands to control gait. A validation model
has been used in order to simulate the real mechani-
cal system (human leg and exoskeleton) in this study.
Further work includes a simulation study of the re-
sponse of the methos to external perturbations (foot
contact with the ground during the swing and obsta-
cles) and testing with subjects of the embedded appli-
cation.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
50

ACKNOWLEDGEMENTS
The authors would like to thank Paschalis Veskos.
The work presented in this paper has been partially
founded by I3P programme of the Spanish Scientific
Research Council.
REFERENCES
Blaya, J. and Herr, H. (2004). Adaptive control of a
variable-impedance ankle-foot orthosis to assist drop
foot gait. IEEE Trans Neural Syst Rehabil Eng,
12(1):24–31.
Forner-Cordero, A., Moreno, J., Cullell, A., Navarro, E.,
and Pons, J. (2006). Evaluation of mental load to wear
an actuated knee ankle foot orthosis. In International
Congress on Gait and Mental Functio, Madrid, Spain.
Franken, H. (1995). Cycle to cycle control of swing phase
of paraplegic gait induced by surface electrical stimu-
lation. Medical and Biological Engineering and Com-
puting, 33:440–451.
Gharooni, S., Heller, B., and Tokhi, M. (2000). A new hy-
brid spring brake orthosis for controlling hip and knee
flexion in the swing phase. IEEE Transactions on Re-
habilitation Engineering, 9(1):106–107.
Goldfarb, M. and Durfee, W. K. (1996). Design of a
controlled-brake orthosis for fes-aided gait. IEEE
Transactions on Rehabilitation Engineering, 4(1):13–
24.
Haverkamp, B., Chou, C., Verhaegen, M., and Johansson,
R. (1996). Identification of continuous-time mimo
state space models fromsampled data, in the presence
of process and measurement noise. In IEEE 35th De-
cision and Control.
Horikawa, S., Furuhashi, T., Okuma, S., and Uchikawa, Y.
(1990). a fuzzy controller using a neural network and
its capability to learn experts control rules. In Proc.
Int. Conf. Fuzzy Logic and Neural Networks, page
103106.
Irby, S., Kaufmaun, K., Wirta, R., and Sutherland, R.
(1999). Optimization and application of a wrap-
spring clutch to a dynamic knee-ankle-foot ortho-
sis. IEEE Transactions on Rehabilitation Engineer-
ing, 7(2):130–4.
Jang, J. (1993). Anfis: Adaptive-network-based fuzzy in-
ference system. IEEE Systems, Man and Cybernetics,
23:665–684.
Moreno, J. (2006). Exosqueletos Robticos para Valoracin
y Compensacin funcional de Marcha Patolgica. PhD
thesis, Universidad Politcnica de Madrid.
Moreno, J., Brunetti, F., Pons, J., Baydal, J., and Barbera, R.
(2005). Rationale for multiple compensation of mus-
cle weakness walking with a wearable robotic ortho-
sis. In International Conference on Robotics and Au-
tomation, pages 1914–1919.
Moreno, J., Rocon, E., Ruiz, A., Brunetti, F., and Pons,
J. (2006). Design and implementation of an inertial
measurement unit for control of artificial limbs: ap-
plication on leg orthoses. Sensors and Actuators B,
118(1-2):333–337.
Perry, J. (1999). Gait Analysis: Normal and Pathological
Function. McGraw-Hill Inc.
Popovic, D., Stein, R., Namik Oguztoreli, M.,
Lebiedowska, M., and Jonic, S. (1999). Opti-
mal control of walking with functional electrical
stimulation: a computer simulation study. Rehabil-
itation Engineering, IEEE Transactions on [see also
IEEE Trans. on Neural Systems and Rehabilitation],
7(1):69–79.
Skelly, M. and Chizeck, H. (2001). Real-time gait event
detection for paraplegic fes waking. IEEE Transac-
tions on Neural Systems and Rehabilitation Ingenier-
ing, 9(1):59–68.
Smith, A. and Brown, E. (2003). Estimating a state-space
model from point process observations. Neural Com-
putation, 15(5):965–91.
Veskos, P. and Demiris, Y. (2006). Neuro-mechanical en-
trainment in a bipedal robotic walking platform. In
Biro-net Symposium, Bristol, UK.
A HYBRID METHOD BASED ON FUZZY INFERENCE AND NON-LINEAR OSCILLATORS FOR REAL-TIME
CONTROL OF GAIT
51
