ON-CHIP FLUORESCENCE LIFETIME EXTRACTION USING

SYNCHRONOUS GATING SCHEME

Theoretical Error Analysis and Practical Implementation

Day-Uei Li, Bruce Rae, David Renshaw, Robert Henderson

Institute for Integrated Micro and Nano Systems, The University of Edinburgh, The King’s Buildings

Mayfield Rd., Edinburgh EH9 3JL, UK

Eleanor Bonnist

School of Chemistry and the Collaborative Optical SpectroscopyMicromanipulation and Imaging Centre (COSMIC)

University of Edinburgh, West Mains Rd., Edinburgh EH9 3JJ, UK

Keywords: Fluorescence lifetime imaging microscopy (FLIM). Error analysis. On-chip implementation. Rapid lifetime

determination (RLD). Single photon avalanche diode (SPAD). Time-correlated single-photon counting

(TCSPC). Data fitting. Pipe-lined RLD. Instrumental response function (IRF).

Abstract: A synchronous gating technique was proposed for fluorescent photon collecting. The two- and multi-gate

rapid lifetime determination (RLD) technique was applied to implement on-chip fluorescence lifetime

extraction. Compared with all available iterative least square method (LSM) or maximum likelihood

estimation (MLE) based general purpose FLIM analysis software, we offer a method for the direct

calculation of lifetime based on the photon counts stored in on-chip memory and deliver faster analysis to

enable real-time applications. Theoretical error analysis of the two-gate RLD technique was derived for

comparison. The performance of the algorithms were tested on a single-exponential histogram obtained

from a CMOS SPAD detector chip using a 468nm laser diode light source with optimized gate width.

Moreover, a multi-exponential pipelined RLD FLIM technique was also proposed and tested on a four-

exponential decay DNA sample containing a single adenine analogue 2-aminopurine.

1 INTRODUCTION

Fluorescence lifetime measurements have been used

widely to study various scientific and practical

applications on optics, chemistry, biology, medicine,

medical diagnosis. A large number of different

techniques including time-domain and frequency-

domain methods have been well developed for

measuring fluorescence lifetime (Apanasovich and

Novikov, 1992). In time-domain methods, the

fluorescence intensity decay is measured through a

time-correlated single photon-counting (TCSPC)

card after excitation with a short pulse of laser light

(Cubeddu et al, 2002), whereas in frequency-domain

methods, the fluorescent sample is illuminated with

a periodic light source to obtain a measured phase

difference between the light source and the

fluorescent emission. Irrespective of the method

used (Jo et al, 2004), the lifetime extraction is done

using computer software. For general purpose time-

domain analysis tools for scientific research

demanding high accuracy down to the picosecond

timescale or for practical medical/clinical diagnostic

applications demanding fast results, a wide range of

faint multi-exponential fluorophores must be

computed with a lifetime resolution better than 50ps

(Becker, 2005). Due to the incapability of the LSM

or MLE to resolve a small lifetime with a coarse

channel width, the number of bits of resolution of

TDCs on photon counting cards is therefore

expected to be larger than 11-bit (Becker, 2005). To

use LSM or MLE properly, the measurement

window is usually set as large as possible otherwise

the software would treat the measured data as having

a DC offset part and therefore the laser pulse

repetition rate is kept low, which further lowers the

photon collection speed. Data therefore can be

gathered in several days. Moreover, because

171

Li D., Rae B., Renshaw D., Henderson R. and Bonnist E. (2008).

ON-CHIP FLUORESCENCE LIFETIME EXTRACTION USING SYNCHRONOUS GATING SCHEME - Theoretical Error Analysis and Practical

Implementation.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 171-176

DOI: 10.5220/0001061301710176

 SciTePress

fluorescence lifetimes in imaging are determined on

a pixel-by-pixel basis, iterative methods can be quite

time consuming and make real-time image

processing almost impossible. Although one can

drop the requirement for short laser pulses by using

frequency-domain methods, lifetime extraction still

relies on software analysis, which also makes real-

time image processing difficult to achieve. As

process technology advances, integration of high

speed laser drivers and laser diodes on chip is

becoming feasible.

2 THEORETICAL ERROR

ANALYSIS

The recorded fluorescence intensity f(t) is related to

the true decay function I(t) through the integral

()()

()

tItIRFd

ττ

=−

∫

(1)

where IRF(t) is the instrumental response function,

or the convolution of transition spread of the

detector and the pulse function of the laser source.

The true response I(t) could be obtained through an

on-chip digital de-convolution calculation. However,

we need to evaluate whether the enhanced precision

can justify the cost of the extra chip area for digital

de-convolution. Here we assume I(t) = Aexp(-t/

τ),

and the ratio of the full width half maximum

(FWHM) of IRF(t) over the lifetime is denoted as r.

The recorded response f(t) is obtained from (1). As r

is larger than 1, it is difficult to obtain a clear

response because of the effects of noise and it is

inefficient to accumulate enough photon counts for a

certain SNR criteria. The smaller the ratio r, the

more efficiently and accurately the lifetime can be

extracted. Considering the 10ps jitter in the light

source, the 80ps transition spread of our SPAD

structure, and the 30ps jitter of gate transitions, the

overall FWHM is about 100ps. Thus, without on-

chip de-convolution function, the smallest lifetime

that can be obtained is of the order of 200ps. For

first time implementation, we simplify by using

longer-lifetime samples as test cases. The

assumption of f(t) as a single exponential is quite

reasonable. In this paper, we applied the RLD

method for simplicity.

2.1 Theory

The simplest way of calculating fluorescence

lifetime is to use the RLD technique with two

consecutive gates (Ballew and Demas, 1989) called

Figure 1: Generalized form of two-gate RLD.

standard RLD. Unlike the LSM or MLE based

methods, it is a direct calculation method. The

disadvantage of standard RLD is its high sensitivity

to the gate width selection. This can be explained by

reasoning that when dealing with a short lifetime,

the photons are mostly located in the first gate, and

the relatively low counts in the second gate becomes

the major source of error. To overcome this problem,

a gate overlap approach was introduced to the

standard RLD (Sharman and Periasamy, 1999)

trying to offer greater insensitivity to the Possion

noise in the second gate. This method did offer

better resolvability for a range of short lifetimes, but

it sacrificed precision for the longer lifetimes.

Another approach called SWRLD is proposed (Chan

et al, 200) using a square wave driven LED as a light

source. SWRLD offers uniform high precision in a

much wider range of gate width. However, this

method does not easily extract lifetimes shorter than

1ns because the 1ns edge speed of the fastest

available LED dictates the minimum lifetime

extraction limit, Thus an example of a long lifetime

of 2ms has been chosen as an illustration. The

second challenge is that SWRLD needs many filters

to separate fluorophore emission from scattered laser

emission (the IRF). Beyond these limits, SWRLD is

indeed a precise method for long lifetime extraction

(>> 10ns). A better approach to achieve better

precision for long lifetimes is make the second gate

wider than the first and therefore tolerate much

higher counts (Moore et al, 2004). This method,

however, needs an iteration method to do lifetime

extraction. Plus for on-chip implementation,

asymmetric gates require the generation of two

synchronized clocks with different pulse widths and

thus increase the circuit complexity. The best

theoretical solution is not necessarily the right one in

terms of cost and feasibility. All the amended

algorithms mentioned require Monte Carlo to do

error analysis. We derive a generalized formula here

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

172

for calculating the standard deviation of lifetimes

much more conveniently and therefore facilitate

location of the optimized lifetime region or

measurement window. Figure 1 shows the

generalized form of two-gate RLD. The counts N

and N

in the two gates are related as

(

)

(

)

() 1 0,

gx N x N x x=−− −=

(2)

where x = exp(-h/

) and

()

(

)

()()

111

222

1/1 , ,

/1 , .

SR R

NN x x N N

NNxx x N N

=−− =

(3)

with σN

and σN

being the standard deviations in

and N

, respectively for Poisson noise and N

the

total count number. Together with (2), we have

(

)

(

)

xxgx

σσ

′

=⋅

(4)

()

gNxNxx

σσ σ

=−+−

(5)

(

)

(

)

gx N NSx Rx

−−

′

=+ −

(6)

and .xx h

στ τ

(7)

From (2) to (7), we could obtain

()

() ()

()

1()

() 1 1 .

SRSR

SR SR

hxkxN

Sx Rx SxRx

kx x x x x x x

στ

−

⎡⎤

−−−−+

⎣⎦

=− − +− −

(8)

2.2 Comparison of RLD-2s and RLD-N

To demonstrate the ability of different RLD schemes,

we fix the measurement window (MW). First we

compute the standard deviation over the lifetime

SNR = σ

in dB. Figure 2 shows the SNR in the

range of

/MW within 0.05 and 1, and gate number

N within 2 and 128 under total counts of 2

. It

shows the SNR plot converges as N > 8 and RLD-2

shows the best resolvability for small lifetime region,

but both RLD-2 and RLD-N could not resolve those

less than 0.1. It means that with a laser source of

repetition rate of 100MHz, they could not resolve

those less than 1ns. Moreover, the complexity of

implementing N-gate RLD on chip is too large. In

terms of implementation, the RLD-2 is much easier

than RLD-N. Figure 3 shows a comparison plot of

lifetime SNR versus lifetime normalized by

measurement window (MW) for theoretical equation

(8), equation for the multi-gate scheme not shown

here, Monte-Carlo RLD methods and the maximum

likelihood estimator (MLE) (Kollner and Wolfrum,

1992).

Figure 2: SNR plot for RLD-N under total counts of 2

Figure 3: SNR plot for RLD-N with total counts of 2

This plot shows the range of lifetime resolvable by

each extraction method for a certain laser repetition

rate. The results obtained by theoretical equations

are marked as solid lines whereas those by Monte-

Carlo methods are indicated by dots. They match

well. We also compare the MLE results and find that

the peak value of the RLD-2 occurs at

/MW =

/(2h)

～

0.2 which is coincident with previously reported

literature. The plot shows the RLD-77 has best

precision and closest to that of MLE only in high

lifetime region, while it has the worst resolvability

for low lifetime region. Un-equal gate scheme (S =

0.5, R = 4.5) offers better resolvability than the

equal gate-width one (S = 0.5, R = 1.5). The one

with S = 0.25 and R = 12.25 suggested by (Moore et

al, 2004) offers the best resolvability for small

lifetime region but sacrifices some precision in the

high lifetime region. In terms of implementation

complexity, feasibility, and limitations on chip, the

equal gate width scheme is the simplest. Of course,

if we insist on implementing an un-equal one given

ON-CHIP FLUORESCENCE LIFETIME EXTRACTION USING SYNCHRONOUS GATING SCHEME - Theoretical

Error Analysis and Practical Implementation

173

that we have conquered the problem of transition

spread of the IRF, we could build an on-chip look-

up table to simplify lifetime extraction. For first time

on-chip implementation, we simplify by using the

equal gate and non-overlap scheme. The overlap

scheme will be implemented in the future. Table 1

lists the summary of RLD schemes. Except the

RLD-N, the others are all possible candidates.

Table 1: Comparison and summary of RLD schemes.

Closed

Form

/MW < 0.1

Resolvability

On-chip

Feasibility

Standard

RLD-2

Yes No

Yes/Look-

up Table

Standard

RLD-N

(N > 2)

Yes No No

Overlap

RLD-2

(R = 1+S)

Yes Yes

Yes/Look-

up Table

Overlap

RLD-2

≠ 1+S)

No Yes

Yes/Look-

up Table

2.3 Synchronous Gating Scheme

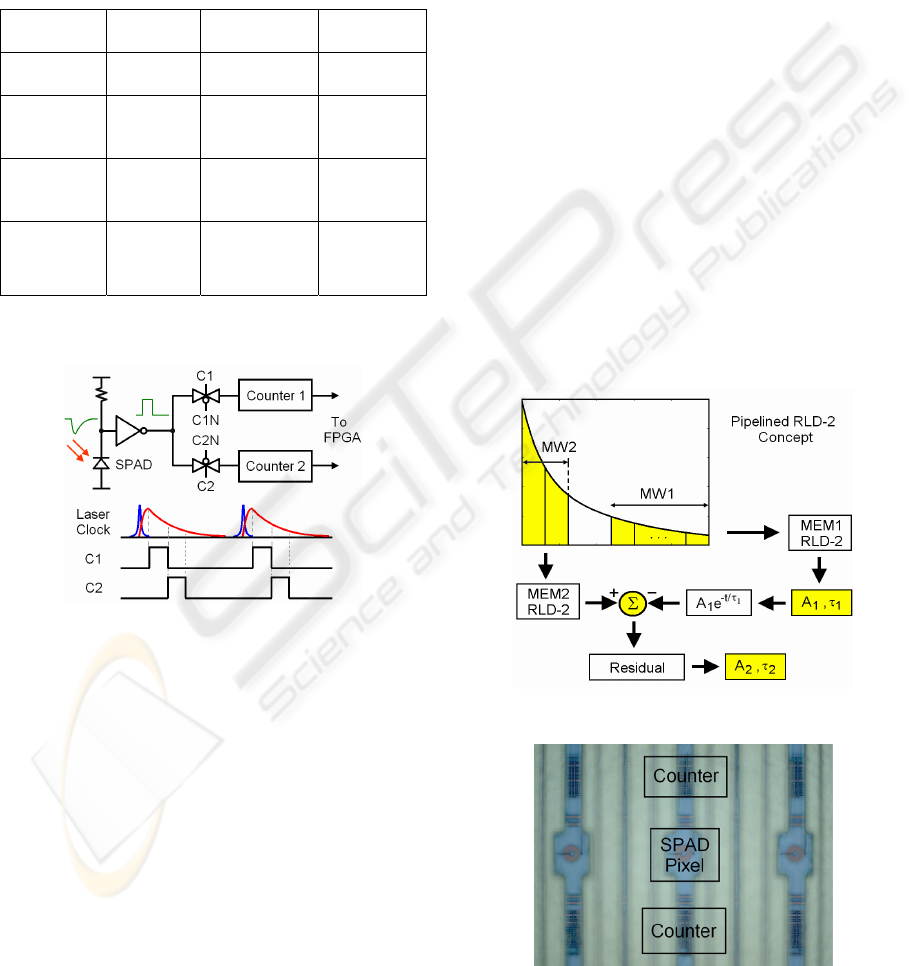
Figure 4: Timing diagram for synchronous gating

technique.

Figure 4 shows the block diagram for the photon

counting process. The fluorescence emission is

detected by a SPAD detector, and the detected signal

is converted into a digital one by a comparator and

then sent into two synchronous counters controlled

by clocks C1 and C2, respectively. And the photon

counts on counters 1 and 2 are sent to a FPGA for

post processing.

2.4 Pipelined RLD-2 for Multi-Decays

The above analysis is based on the assumption that

the fluorescence emission follows a single-lifetime

function. When trying to resolve multi-lifetime

fluorescence decay, we need a simple algorithm.

Figure 5 shows an algorithm for lifetime extraction

in a two-lifetime fluorescence histogram similar to

the concept of pipelined analog-to-digital converters,

called pipelined RLD-2 (PL-RLD-2). The lifetime

extraction procedure uses RLD-2 to extract the

larger lifetime and intensity with the first memory,

and subtraction of the extracted extrapolation

function from the photon counts stored in the second

memory to obtain the second lifetime and intensity.

Pipelined algorithms for higher (> 2) decays can

follow this procedure until the last lifetime is finally

calculated.

3 EXPERIMENTAL RESULTS

3.1 Single-decay

The chip including a 4×16 SPAD array and digital

readout circuits was implemented on 0.35μm high

voltage CMOS process. The die had the polymide

passivation removed providing around 3-5x increase

in photon detection probability in the 500nm range.

Each pixel contains a single 15μm-diameter CMOS

SPAD (Niclass, 2006).

Figure 5: Block diagram of pipelined RLD-2.

Figure 6: SPAD pixel and two ripple counters.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

174

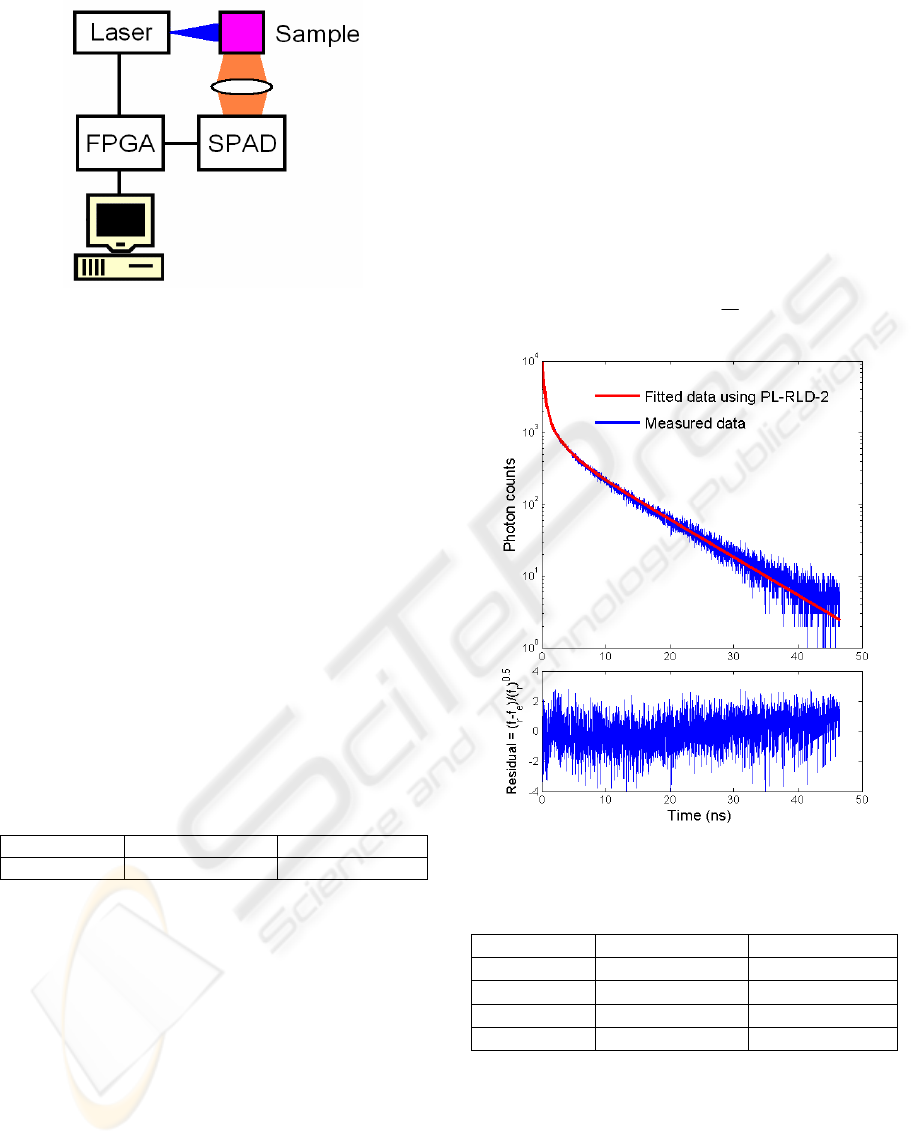
Figure 7: SPAD pixel and two ripple counters.

Figure 6 shows a SPAD pixel with two ripple

counters up and down. The gating width could be

adjusted over a 48ns range with a 408ps resolution.

The imager is controlled by a FPGA and photon

count histograms are captured and displayed on a PC.

The measurement setup is shown in Figure 7. It

consists of a laser diode emitting 88ps pulses at

468nm, 5mW average power, synchronized to the

system clock. Without using any photon counting

card, the photon emitted is converted into a digital

signal and processed by on-chip ripple counters in

Figure 4. The fluorophore sample is 1 micro-molar

Rhodamine B. Table 2 shows the extracted lifetime

using the RLD-2 and the LSM based software. The

difference between them is about 7%. Jitter

performance of the synchronous gate might

contribute some error, because a phase-locked loop

PLL has not been integrated to minimize the jitter.

Table 2: Comparison of lifetimes extracted by RLD-2 and

software.

Sample RLD-2 Software

Rhodamine B 2.33ns 2.175ns

3.2 Multiple-decays

The second example is used to test the proposed

pipelined RLD-2 algorithm. This data set comes

from the fluorophore 2-aminopurine (2AP) inside a

singly-labelled 14 base-pair DNA duplex and was

measured in an Edinburgh Instruments spectrometer

equipped with TCC900 photon counting electronics

(Neely et. al, 2005). The excitation source was a Ti-

Sapphire femtosecond laser system producing pulses

of ~200fs at 76MHz repetition rate. The output of

the laser was passed through a pulse picker to reduce

the repetition rate to 4.75MHz and then frequency

tripled to give an output at 320nm. The emission

from the sample was collected orthogonal to the

excitation direction through a polarizer. The

fluorescence was passed through a monochromator,

and detected by a Hamamatsu PMT (R3809U-50).

The instrument response was 50ps FWHM.

Florescence decay curves were recorded at emission

wavelength of 390nm on a timescale of 50ns,

resolved into 4096 channels, to a total 10,000 counts

in the peak channel. Decay curves were analyzed

using the proposed PL-RLD-2 and using the F900

software with standard iterative reconvolution

method, assuming a multi-exponential decay

function in the following equation.

() exp ,

It A

⎛⎞

=−

⎜⎟

⎝⎠

∑

(9)

Figure 8: Fitted data and residual using PL-RLD-2.

Table 3: Comparison of lifetimes (ns) and fractional

amplitudes (%) extracted by PL-RLD-2 and F900 software.

(ns)/A

(%)

PL-RLD-2 F900 Software

0.136/27 0.14/47

0.481/55 0.47/39

2.179/11 2.19/9

8.225/7 8.15/5

where A

is the fractional amplitude and

is the

fluorescence lifetime of the i-th decay component.

Figure 8 shows the logarithmic plot for the measured

photon counts starting from the channel with peak

counts 10,000 and the fitted data using the proposed

PL-RLD-2. The residual plot reveals that the

proposed method fits well with the experimental

data. The extracted lifetimes and fractional

ON-CHIP FLUORESCENCE LIFETIME EXTRACTION USING SYNCHRONOUS GATING SCHEME - Theoretical

Error Analysis and Practical Implementation

175

amplitudes using the PL-RLD-2 and the F900

software are listed in Table 3. The Table shows the

extracted lifetimes differ within 4% whereas the

amplitudes differ in a significant range. That is why

recent literature (Philip, 2003) suggests that

fluorescence lifetime measurements offer better

precision. These results highlight the potential of

RL-RLD-2 for on-chip multiple exponential lifetime

extraction, if adaptive gating width technique could

also be introduced on-chip.

4 CONCLUSIONS

On-chip fluorescence lifetime extraction including a

SPAD array and digital readout circuitry is for the

first time implemented on 0.35μm CMOS process

using the two-gate RLD. Theoretical error equations

for several RLD-2/RLD-N schemes were derived

and compared to determine a possible

implementation strategy. To implement RLD-2, a

non-overlap synchronous gating is applied for

photon counting. The first on-chip attempt is mainly

focused on dealing with single-exponential

fluorescence emission, and the extracted result

matches with the true value well within 10%

including possible contribution from gating jitter.

For possible future on-chip implementation for

multi-exponential fluorescence lifetime extraction,

we proposed a pipelined RLD-2 (PL-RLD-2) and we

test this method on a four-exponential experimental

data, and the extracted lifetimes match well with

those obtained by iteration based software within 4%.

ACKNOWLEDGEMENTS

This work has been supported by the European

Community within the Sixth Framework Programme

IST FET Open MEGAFRAME project (contract No.

029217-2, www.megaframe.eu). The measurements

have been performed using the COSMIC laboratory

facilities at the University of Edinburgh.

DISCLAIMER

This publication reflects only the authors’ views.

The European Community is not liable for any use

that may be made of the information contained

herein.

REFERENCES

Apanasovich, V. V. and Novikov, E. G. (1992) ‘Methods

of analysis of fluorescence decay curves in pulsed

fluorometry (Review)’, Journal of Applied

Spectroscopy, Vol. 56, No. 4, pp. 317-327.

Cubeddu, R., Comelli, D., D’Andrea, C., Taroni, P. and

Valentini, G. (2002) ‘Time-resolved fluorescence

imaging in biology and medicine’, J. Phys. D: Applied

Physics, Vol. 35, pp. R61-R76.

Jo, J. A., Fang, Q., Papaioannou, T. and Marcu, L. (2004)

‘Novel ultra-fast deconvolution method for

fluorescence lifetime imaging microscopy based on

the Laguerre expansion technique’, Conference

Proceedings, 26

Annual International Conference of

the IEEE EMBS, pp. 1271-1274.

Becker, W. (2005), Advanced Time-Correlated Single

Photon Counting Techniques, Wolfgang, Springer.

Ballew, R. M. and Demas, J. N. (1989), ‘An error analysis

of the rapid lifetime determination method for the

evaluation of single exponential decays’, Ana. Chem.,

Vol. 61, pp. 30-33.

Sharman, K. K. and Periasamy, A. (1999), ‘Error analysis

of the rapid lifetime determination method for double-

exponential decays and new windowing schemes’,

Ana. Chem., Vol. 71, pp. 947-952.

Chan, S. P., Fuller, Z. J., Demas, J. N., Ding, F. and

DeGraff, B. A. (2001), ‘New method of rapid

luminescence lifetime determination using square-

wave excitation’, Applied Spectroscopy, Vol. 55, No.

9, pp. 1245-1250.

Moore, C., Chan S. P., Demas, J. N. and DeGraff, B. A.

(2004), ‘Comparison of methods for rapid evaluation

of lifetime of exponential decays’, Applied

Spectroscopy, Vol. 58, No. 5, pp. 603-607.

Kollner, M. and Wolfrum, J. (1992), ‘How many photons

are necessary for fluorescence-lifetime

measurements?’, Chemical Physics Letters, Vol. 200,

No. 1,2, pp. 199-204.

Niclass, C. L. et al, (2006), ‘A single photon avalanche

diode array fabricated in deep submicron technology’,

Conference Proceedings, Design, Automation, and

Test Europe Conference, pp. 81-86.

Neely, R. K., Daujotyte, D., Grazulis, S., Magennis, S. W.,

Dryden, D. T. F., Klimasauskas, S. and Jones, A. C.,

(2005), ‘Time-resolved fluorescence of 2-aminopurine

as a probe of base flipping in M.Hhal-DNA

complexes’, Nucleic Acids Research, Vol. 33, No. 22,

pp. 6953-6960.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

176