DYNAMICAL PROPERTY OF PERIODIC OSCILLATIONS

OBSERVED IN A COUPLED NEURAL OSCILLATOR NETWORK

FOR IMAGE SEGMENTATION

Tetsuya Yoshinaga and Ken’ichi Fujimoto

Faculty of Medicine, The University of Tokushima

3-18-15 Kuramoto, Tokushima, 770-8509 Japan

Keywords: Coupled oscillator, image segmentation, dynamical system, bifurcation.

Abstract: We consider image segmentation using the LEGION (Locally-Excitatory Globally-Inhibitory Oscillator Net-

work), and investigate dynamical properties of a modiﬁed LEGION, described by noise-free or deterministic

continuous ordinary differential equations. We clarify a phenomenon of image segmentation corresponds to

the appearance of a synchronized periodic solution, and the ability of segmentation depends on its symmet-

ric properties. We study bifurcations of periodic solutions by using a computational method based on the

qualitative dynamical system theory.

1 INTRODUCTION

Image segmentation technique underlies perceptual

processes such as identiﬁcation, recognition, and sep-

aration of different objects in a natural image. Vari-

ous methods of image segmentation based on statis-

tic, ﬁltering, and machine learning techniques were

presented (Russ, 2002). A practical image seg-

mentation technique using the LEGION (Locally-

Excitatory Globally-Inhibitory Oscillator Network)

has alsobeen proposed (Wang and Terman, 1995; Ter-

man and Wang, 1995). It can segment different areas

in an image, and then the segmented areas are rapidly

exhibited in time-series. Because of the high ability

of LEGION, there has been a lot of research on appli-

cation to medical images (Shareef et al., 1999), im-

plementation of analog electronic circuit (Cosp et al.,

2004), and so on.

The LEGION is a coupled oscillator network con-

sisting of oscillators, each of which has an excitatory

unit and an inhibitory unit, and a global inhibitor. The

dynamics of LEGION is described by nonlinear or-

dinary differential equations with a noise term. It is

know that LEGION segments different image areas

temporally and spatially, based on its own dynamics.

Although its fundamental dynamics has been stud-

ied (Terman and Wang, 1995), there are no investi-

gations for detailed dynamical structure and property

of oscillations observed in the coupled oscillator net-

work. Properties of the oscillations observed in LE-

GION are related to its fundamental ability for im-

age segmentation, therefore analysis of the dynamical

properties enable us to design the parameters of LE-

GION so that it achievesoptimal image segmentation.

In this paper we study dynamical properties of os-

cillations observed in LEGION. Because the dynam-

ics of the original LEGION (Wang and Terman, 1995)

is a stochastic dynamical system with noise terms, in

order to simplify our discussion, we study a noise-free

LEGION, which is a deterministic dynamical system.

Bifurcation analysis is useful for designing system pa-

rameter. Through the bifurcation analysis, we clar-

ify that a phenomenon of image segmentation corre-

sponds to the appearance of a synchronized periodic

solution, and the ability of segmentation depends on

its symmetric properties.

2 MODEL DESCRIPTION

The LEGION consists of a global inhibitor and oscil-

lators which are arranged in grid; and the number of

oscillators corresponds to the number of pixels in tar-

get image. We illustrate single oscillator which con-

sists of an excitatory unit EU

and an inhibitory unit

in Fig.1 (a). The excitatory unit couples with

the other excitatory units in its four-neighborhood

141

Yoshinaga T. and Fujimoto K. (2008).

DYNAMICAL PROPERTY OF PERIODIC OSCILLATIONS OBSERVED IN A COUPLED NEURAL OSCILLATOR NETWORK FOR IMAGE SEGMENTA-

TION.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 141-146

DOI: 10.5220/0001062101410146

 SciTePress

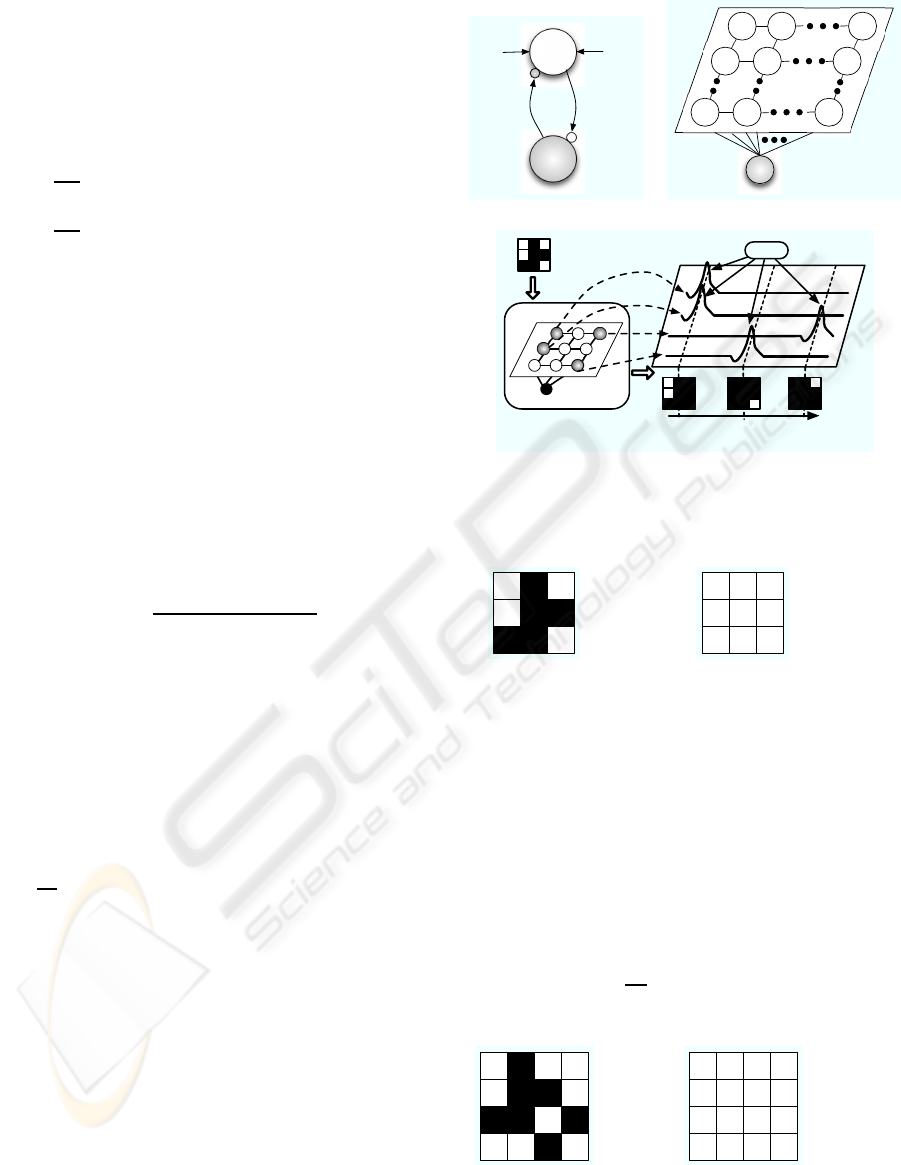
each other, and all excitatory units also connect to

the global inhibitor. The architecture of LEGION is

shown in Fig.1 (b). Figure 1 (c) illustrates the behav-

ior of LEGION and schematic diagram of an image

segmentation procedure. The dynamics of an oscilla-

tor indexed by i (i = 1,2,... ,n) is described by

= 3x

− x

+ 2− y

+ I

(1)

= η[γ(1 + tanh(x

/β)) − y

]. (2)

We eliminated noise terms from the original LE-

GION (Wang and Terman, 1995) so that the system

becomes a deterministic dynamical system. The vari-

ables x

and y

represent the states of the excitatory

and inhibitory units, respectively. The symbol I

de-

notes external stimulation to the oscillator. Its value is

determined by the i-th pixel value. The symbolC

rep-

resents the summation of the coupling strength among

oscillators, which is deﬁned by

∑

k∈N(i)

S(x

,θ

) −W

S(z,θ

) (3)

where

S(x,θ) =

1+ exp(−K(x− θ))

. (4)

Here N(i) indicates the four-neighborhood of the i-th

oscillator, W

denotes the coupling strength between

the i-th oscillator and the other k-th oscillator in N(i),

and W

denotes the coupling strength between the i-

th oscillator and the global inhibitor. Using the sig-

moidal function, described by Eq.(4), instead of the

Heaviside function in the original LEGION, the dy-

namics of the global inhibitor is deﬁned by

= φ

∑

k=1

S(x

,θ

),θ

− z

(5)

where γ, β, θ

, θ

, K, and φ indicate parameters,

which are ﬁxed as the same values of the original

γ = 6.0, β = 0.1, θ

= −0.5

= θ

= 0.1, K = 50, φ = 3.0 (6)

and η is a bifurcation parameter.

We treat binary images shown in Figs. 2–3; the in-

dexes of the pixels are also shown in the same ﬁgures.

For the binary images, the value of I

is determined by



> 0, if the i-th pixel is white

< 0, if the i-th pixel is black.

(7)

Inhibitory

Excitatory

connection

l+1

l+2

lr+1

lr+2

(a) (b)

Input image

LEGION

Time

Fire

Output images

(c)

Figure 1: (a), (b) Architecture of LEGION, and (c) behavior

of LEGION and schematic diagram of image segmentation.

6 9

(a) Input image (b) Index number of each pixel

Figure 2: (3× 3)-pixel image and its index number of each

pixel.

3 METHOD OF ANALYSIS

We summarize methods for calculating bifurcations

in the deterministic LEGION deﬁned in the preceding

section. Let us consider an N-dimensional general au-

tonomous differential equation consisting of Eqs.(1)–

(5) such that

= f(x). (8)

(a) Input image (b) Index number of each pixel

Figure 3: (4× 4)-pixel image and its index number of each

pixel.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

142

-3

-2

-1

0 100 200 300 400 500 600

t −→

, x

−→

(a)

-3

-2

-1

0 100 200 300 400 500 600

t −→

, x

−→

(b)

-3

-2

-1

0 100 200 300 400 500 600

t −→

, x

−→

(c)

-3

-2

-1

0 100 200 300 400 500 600

t −→

, x

−→

(d)

Figure 4: Waveforms of stable periodic solutions under η = 0.02. The thin solid curve indicates the states of the oscillators

and x

; and the heavy solid curve and the dashed curve denote the states of the oscillators x

and x

, respectively.

DYNAMICAL PROPERTY OF PERIODIC OSCILLATIONS OBSERVED IN A COUPLED NEURAL OSCILLATOR

NETWORK FOR IMAGE SEGMENTATION

143

The state vector x ∈ R

corresponds to the set

,.. .,x

,z} ∈ R

2n+1

, where n denotes

the number of oscillators. Note that f(x) is C

∞

-class

function for all state variables and all parameters. We

assume that there exists a solution with initial condi-

tion, x = x

at t = t

, described by x(t) = ϕ(t;x

) for

all t.

We consider a local manifold Σ in the N-

dimension state space with the scalar condition

g(x) = 0, which is described by

Σ =



x ∈ R

| g(x) = 0, g : R

→ R



. (9)

We arrange a local section Π ⊂ R

N−1

in Σ called the

Poincar´e section. Using the coordinate transforma-

tion h described by

h : Σ → Π ⊂ R

N−1

; x 7→ u, (10)

we deﬁne the Poincar´e map T as

T : Π → Π; u 7→ h◦ ϕ



τ(h

−1

(u));h

−1

(u)



(11)

where τ(h

−1

(u)) is the time in which the trajectory

emanating from a point u ∈ Π at t = t

will go across

the Π again. Then an m-periodic solution in Eq.(8)

corresponds to a ﬁxed point of T

, i.e., m-periodic

point of T. Hence, one of analyses of m-periodic solu-

tions observed in Eq.(8) can be reduced to an analysis

of a ﬁxed point of T

Let u

∗

∈ R

N−1

be a ﬁxed point of T

such that

∗

− T

∗

) = 0. (12)

Then the characteristic equation of the ﬁxed point is

deﬁned by

χ(µ) = det



µI

N−1

−

∂T

∗

)

∂u



= 0 (13)

where I

N−1

is the (N − 1) × (N − 1) identity ma-

trix. By using the Poincar´e map T

we totally have

2(N − 1)-different-type hyperbolic ﬁxed points. The

topological property of a hyperbolic ﬁxed point is de-

termined by the value of characteristic multipliers µ

(i = 1,2,..., N − 1): if all characteristic multipliers

are in the unit circle on the Gaussian plane, then the

ﬁxed point is stable; the ﬁxed point is unstable if one

or more characteristic multipliers are outside the unit

circle. Hence, we can discuss topological property of

the ﬁxed point based on the value of the characteris-

tic multipliers. Let us classify ﬁxed points into two

types

D and

I, where k is the number of characteris-

tic multipliers outside the unit circle; it also represents

the dimension of unstable subspace. The types D and

I correspond to the even and odd numbers of charac-

teristic multipliers in the range of (−∞, −1) on the

real axis, respectively. Bifurcation of a ﬁxed point oc-

curs when its topological property is changed by the

variation of a system parameter. The types of bifur-

cations are tangent bifurcation, period-doublingbifur-

cation, the Neimark-Sacker bifurcation, and D-type of

branching. Bifurcation sets of a ﬁxed point are com-

puted (Kawakami, 1984) by solving the simultaneous

equation which consists of Eqs.(12)–(13).

Now, let us discuss a symmetrical property of the

system in Eq.(8). Assume that there exists a trans-

formation Q satisfying Q( f(x)) = f(Q(x)). Then

such a system may have a periodic solution satisfy-

ing Q(ϕ(t;x

)) = ϕ(t + L;x

) for all t, where L ≥ 0

is a phase difference. We call it a (Q, L)-symmetric

periodic solution.

4 RESULTS AND DISCUSSION

This section is devoted to show and discuss numerical

results obtained from bifurcation analysis of a couple

of examples.

4.1 Example 1

We investigate periodic solutions observed in the de-

terministic LEGION for 3 × 3 pixel image shown in

Fig.2. Each external stimulus I

, i = 1, 2,...,9, is de-

ﬁned as



= 0.2, if the i-th pixel is white

= −0.02, if the i-th pixel is black.

(14)

Because the pixels indexed by 1, 2, 7, and 9 are white,

we observe oscillatory responses from the oscillators

with the same indices, and non-oscillatory responses

from the other oscillators. Note that, because the set

satisfying x

≡ x

and y

≡ y

is an invariant subspace

in the state space, the system is symmetric with re-

spect to the transformation, say Q

, swapping (x

)

and (x

For oscillatory solutions we use symbolic se-

quence of strings representing the continuation of in-

phase ﬁring assigned by the oscillator indices and

non-ﬁring assigned by dot (“.”). For example, the set

of (12.79.7.9) indicates a sequence in the order of ﬁr-

ing: oscillators 1 and 2 (instantaneously in-phase), os-

cillators 7 and 9 (instantaneously in-phase), oscillator

7, and oscillator 9, periodically.

Figure 4 shows waveforms of stable periodic so-

lutions observed in the system at η = 0.02. The sym-

bolic sequences corresponding to Figs.4 (a)–(d) are,

respectively, as follows: (a) (12.79.79.12.79); (b)

(12.7.9.7.12.9.7.9); (c) (12.7.9.7.9.12.7.9); and (d)

(12.9.7.9.7.12.9.7). The solutions shown in Figs.4

(a) and (b) are (Q

,0)- and (Q

,τ/2)-symmetric two-

periodic solutions, respectively, where τ denotes the

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

144

period of solution. While, each of the solutions shown

in Figs.4 (c) and (d) has no symmetric property itself,

however, it is reﬂectional with respect to the trans-

formation Q

each other. We show the time-series of

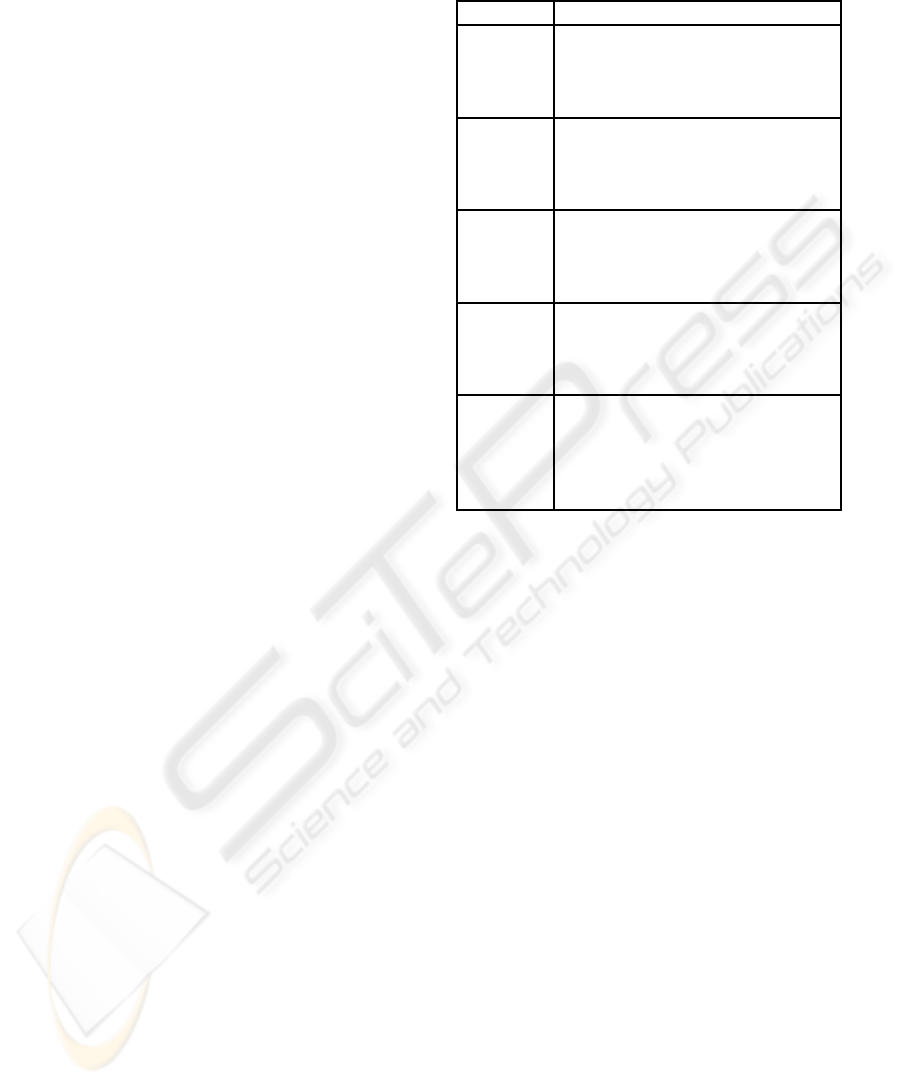
output images from LEGION in Fig.5, which corre-

sponds to the solution of Fig.4 (b). The connected

white pixels, the ﬁrst pixel and the second pixel, al-

ways appear instantaneously in-phase. Then three dif-

ferent image areas are segmented temporally and spa-

tially.

Figure 5: Snapshots of time-series output in LEGION

which corresponds to the periodic solution shown in Fig.

4 (b). These output images sequentially appear from on the

top-left to the bottom-right; then its appearance in each line

starts from the left.

We investigate bifurcations of periodic points

based on the Poincar´e section deﬁned by

Π =



x ∈ R

| x

− 1.5 = 0,

< 0



. (15)

Figure 6 shows a one-parameter bifurcation dia-

gram of a (Q

,0)-symmetric two-periodic solution as

shown in Fig.4 (a). In the bifurcation diagram, the

heavy curve denotes stable (Q

,0)-symmetric two-

periodic solution, and the dashed curve indicates its

destabilized solution. The circled point labeled by I

denotes the parameter value η = 0.08098952872, at

which we observe a period-doubling bifurcation. By

decreasing the value of η across the point, the follow-

ing bifurcation formula occurs:

→

(16)

where the left- and right-hand sides of the arrow indi-

cate the periodic points before and after the bifurca-

tion, respectively. Hence, a stable two-periodic solu-

tion

and a saddle-type four-periodic solution

simultaneously occur, i.e., they coexist in a certain pa-

rameter region. Let us discuss the basin of the stable

solution. Figure 7 (a) shows periodic points of the

Poincar´e map at η = 0.0808, projected to the (x

plane. The points a and b indicates two-periodic point

, and the points c and d correspond to a (Q

,τ/2)-

symmetric two-periodic solution, which is irrelative

to the bifurcation in Eq.(16). The periodic points of

the coexisting

are near the point a. It can be con-

ﬁrmed by the phase portrait shown in Fig.7 (b), an en-

larged ﬁgure of Fig.7 (a); the points e and f denote a

8305

1.83

8295

.829

0.075 0.076 0.077 0.078 0.079 0.08 0.081 0.082

−→

η −→

Figure 6: One-parameter bifurcation diagram of x

for the

parameter η. The thin solid curve, the heavy solid curve,

and the dashed curve denote the unstable four-periodic

point, the stable two-periodic point, and its destabilized

two-periodic point, respectively.

-1.9

1.85

-1.8

1.75

-1.7

1.65

-1.9 -1.85 -1.8 -1.75 -1.7 -1.65

−→

7185

7184

7183

-1.7185 -1.7184 -1.7183

−→

(a) (b)

Figure 7: Phase portrait of periodic points on the (x

plane under η = 0.0808. The right ﬁgure is the enlarged

ﬁgure around the point a in the left ﬁgure.

part of four-periodic points

. The period-doubling

bifurcation of

occurs so that its symmetry is bro-

ken, then the placement of the periodic points are re-

ﬂected in the topological property which can be ex-

plained by its eigenvector. Besides, the basin bound-

ary of

is separated by the stable manifold of

That is, we can observe

when the initial value is

placed only near its periodic point.

4.2 Example 2

As the second example we treat 4 × 4 pixel image

shown in Fig.3. The value of each external stimu-

lus I

, i = 1,2,.. .,16, is deﬁned by Eq.(14); its in-

dex number i is shown in Fig.3 (b). Due to the pix-

els indexed by 1, 2, 4, 8, 9, 11, 13, 14, and 15

are white, the dynamical system has two symme-

tries for two swapping operators. One is described

by Q

( f(x)) = f (Q

(x)) where Q

is the transfor-

mation that swaps (x

) with (x

respectively. The other symmetry is described by

( f(x)) = f(Q

(x)) where Q

is the transformation

that swaps (x

) with (x

). In this exam-

ple, we investigate periodic solutions with the follow-

ing relations: (x

) = (x

), (x

) = (x

and (x

) = (x

). Periodic solu-

DYNAMICAL PROPERTY OF PERIODIC OSCILLATIONS OBSERVED IN A COUPLED NEURAL OSCILLATOR

NETWORK FOR IMAGE SEGMENTATION

145

tions in Table 1 are observed under η = 0.02. Note

that we employed the symbols a,b, c,... ,g instead of

the double-digit index numbers 10,11,12, ...,16, re-

spectively. Besides, the symbols A, B, C, D, and

E represent kinds of periodic solutions. All solu-

tions in the category A are (Q

,0)-symmetric two-

periodic solutions; the solutions A

and A

are re-

ﬂectional symmetry for Q

, then A

and A

are also

reﬂectional symmetry for Q

. The category B indi-

cates (Q

,0)-symmetric two-periodic solution, then

and B

are reﬂectional symmetry for Q

. The cate-

gory C denotes (Q

,τ/2)-symmetric two-periodic so-

lution, then C

and C

are also reﬂectional symmetry

for Q

. Each periodic solution in D has two sym-

metries. The category D

is a two-periodic solution

with (Q

,0)- and (Q

,0)-symmetric properties; the

others D

, D

, and D

are two-periodic solutions with

,0)-symmetric and (Q

,τ/2)-symmetric. All so-

lutions in E are asymmetric two-periodic solutions,

however, respective pairs of solutions (E

) and

) are reﬂectional symmetry for Q

. The solu-

tions (E

) and (E

) are also reﬂectional sym-

metry for Q

, respectively. Besides, in the solutions

, A

, B

, C

, D

, and E

, the image

area connected white pixels, indexed by 9, 13, and 14,

synchronously ﬁre with the other white area, e.g., the

pixels indexed by 1, 2, 4, or 8. This synchronization

is interesting from a viewpoint of nonlinear science.

However, it is inappropriate for image segmentation.

5 CONCLUDING REMARKS

We have investigated dynamical properties of peri-

odic solutions observed in the deterministic LEGION,

which is a modiﬁcation from the original one by elim-

inating noise terms and replacing the Heaviside func-

tion with a sigmoidal function, in order to investi-

gate dynamical properties and ability of LEGION.

The main results obtained from the analysis using our

method for computing bifurcation sets, are summa-

rized as follows: (1) The dynamical system has var-

ious kinds of symmetric properties corresponding to

the input image. Indeed we see that symmetric and

asymmetric periodic solutions can be observed. Its

patterns are based on the symmetric dynamical struc-

ture of LEGION; (2) A stable symmetric periodic so-

lution bifurcates under a certain parameter. Moreover,

then its basin boundary is determined by the stable

manifolds of the coexisting saddle-type periodic solu-

tion; and (3) We also observed periodic solutions such

that different image areas ﬁre synchronously. The in-

trinsic objective of image segmentation in LEGION

is that different image areas are not exhibited at the

Table 1: Periodic solutions by symbolic sequences.

Category Periodic solutions

(1248.b.g.9de.b.g.1248.b.g.9de)

(1248.g.9de.b.1248.g.b.9de.g.b)

(12489de.g.b.g.b.12489de.g.b)

(12489de.b.g.b.g.12489de.b.g)

(12.48.bg.9de.12.bg.48.9de.bg)

(12.9de.bg.48.12.bg.9de.48.bg)

(129de.bg.48.129de.bg.48.bg)

(12.bg.489de.12.bg.489de.bg)

(12.g.9de.b.48.g.12.b.9de.g.48.b)

(12.g.48.b.9de.g.12.b.48.g.9de.b)

(129de.g.b.48.g.129de.b.g.48.b)

(12.g.b.489de.g.12.b.g.489de.b)

(12489de.bg.12489de.bg.bg)

(1248.g.9de.b.g.1248.b.9de.g.b)

(1248.b.g.9de.b.1248.g.b.9de.g)

(12489de.g.b.g.12489de.b.g.b)

(12.g.b.48.9de.g.b.12.48.g.b.9de)

(12.b.g.48.9de.b.g.12.48.b.g.9de)

(12.b.g.9de.48.b.g.12.9de.b.g.48)

(12.g.b.9de.48.g.b.12.9de.g.b.48)

(12.b.g.489de.12.b.g.489de.b.g)

same time. Therefore, the appearance of the periodic

solutions is inappropriate for this objective.

Their analyzed dynamical properties are directly

related to fundamental abilities of LEGION. For

higher quality of the segmentation, a mechanism for

desynchronizing in-phase periodic solutions is re-

quired in the coupling system.

REFERENCES

Cosp, J., Madrenas, J., Alarcon, E., Vidal, E., and Villar, G.

(2004). Synchronization of nonlinear electronic os-

cillators for neural computation. IEEE Trans. Neural

Networks, 15(5):1315–1327.

Kawakami, H. (1984). Bifurcation of periodic responses

in forced dynamic nonlinear circuits: computation of

bifurcation values of the system parameters. IEEE

Trans. Circuits Syst., CAS-31(3):246–260.

Russ, J. (2002). The image processing handbook, fourth Ed.

CRC Press.

Shareef, N., Wang, D., and Yagel, R. (1999). Segmentation

of medical images using legion. IEEE Trans. Medical

Imaging, 18:74–91.

Terman, D. and Wang, D. (1995). Global competition and

local cooperation in a network of neural oscillators.

Physica, D81:148–176.

Wang, D. and Terman, D. (1995). Locally excitatory glob-

ally inhibitatory oscillator networks. IEEE Trans.

Neural Networks, 6(1):283–286.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

146